0 引言

作为决策粗糙集^[1]的核心思想之一，三支决策理论近年来在各方面^[2-11]均取得了长足的进展。各种先进的理论如形式三支粒计算、三支概念分析、三支认知计算、三支模糊集方法、三支决策空间^[2-7]等均受到三支决策的启发。此外，在三支决策基础上又实践了多种机器学习技术，如三支推荐系统、三支主动学习、三支聚类^[8]、三支邻域覆盖约简^[9]、三支垃圾邮件过滤^[10]、项集三支增量挖掘^[11]等。

增量算法利用已有的知识和增量数据得到最新的知识^[11]，能够极好地适应大数据场景。对于模式发现问题，人们针对购物数据提出了频繁项集的增量算法如三支决策更新模式方法(three-way decision update pattern，TDUP)^[11]和快速更新算法(fast update，FUP)^[12]。对于各种序列数据，如股价、文本、基因，设计了频繁闭合序列挖掘算法(incremental bide，BideInc)^[13]。对于最一般的时序交互数据^[14]，如出行轨迹、购物清单、观影评分^[15]等，大量的增量算法如增量序列提取(incremental sequence extraction，ISE)^[16]和增量更新序列(incrementally updating sequences，IUS)^[17]被提出来获得频繁的事件/行为序列。多元时序数据(multivariant time series, MTS)如空气质量、工业设备、人体健康数据上的频繁模式^[18]挖掘同样受到了广泛关注^[19-20]。然而，MTS上的频繁模式增量挖掘算法还有待丰富。

本文提出了MTS数据上状态转移模式(state transition pattern，STAP)^[20]的三支增量挖掘算法(three-way incremental updating method of state transition pattern，3IU-STAP)。该算法由4个阶段组成。第一，增量更新频繁状态。它们是构成STAP的基本分量元素，其集合可被视为构成STAP的字母表。第二，构造候选STAP以及增补数据db′。任意候选STAP均是由两个更短的频繁STAP链接而来。从原始数据DB截取的尾部长度是由候选序列的长度和通配符区间的上界来确定的。对于所有长度相同的候选STAP，所截取的尾部是一致的。因此，在最坏情况下，构建增补数据的次数为MTS数据的长度；而在平均情况下，其构建次数与最长频繁STAP的长度一致。第三，通过判断候选STAP在DB和db′上频繁或不频繁的表现，将所有候选模式划分进3个互不相交的集合中，即正域(positive region，POS)、负域(negative region，NEG)和边界域(boundary region，BND)。当一个候选STAP在DB和db′上均频繁，则它一定是频繁的，令其属于正域。当一个候选STAP在DB和db′上均不频繁，则它一定是不频繁的，令其属于负域。否则，将其划入边界域，通过重新扫描DB或db′获得准确的支持度，并判断该STAP是否频繁。第四，算法依靠所获得的频繁模式来构造更长的候选模式，直到生成候选模式集合为空时终止。

对环境工程、工业设备、石油工程等领域的4个真实数据集进行实验，结果表明，增量算法与批量算法相比，时间性能提高了5.3~649倍，且增量越小，效率越高。

1 基础知识

本章首先介绍MTS的数据模型。在此基础上描述状态、STAP及其支持度。

1.1 数据模型

定义1^[20]  MTS是一个四元组$D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right) $, 其中：T={t₁, t₂, …, t_n}代表时间点的集合；A={a₁, a₂, …, a_m}是一组变量集；V_a是变量a的值的范围；f:T×A→V是一个映射函数。此外，t_i+t_i+2=2t_i+1(1≤i≤|T|－2)，则称时序数据MTS是周期型的。

在模式挖掘过程中，人们通常关注符号型的MTS数据。对于传感器网络采集的数值型数据，需要进行离散化。

1.2 状态转移模式

任意给定一个符号型多元时间序列，其描述的系统所有可能状态的数量为$\prod\limits_{a \in A}\left(\left|V_{a}\right|+1\right)-1 $。这是因为属性a有|V_a|+1个可能的属性值。一个状态集中的各个属性的取值不会在单位时间内同时发生，即是互斥的。然而，状态数量对于属性数量是指数级的。因此，根据阈值ρ_w实现的频繁状态挖掘算法是有效的解决方案。此外，尽管状态的形式与项集一致，但是状态比项集的语义更加丰富，具有“特殊”与“一般”的概念。MTS中的任意一行记录的是系统在当前时间点的最特殊状态，其任意子集均是该状态的“一般”状态。项目的空集∅表示该系统最“一般”状态。

定义2^[20]  给定$ D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right)$和Δ=[G, G]，带通配符区间的状态转移模式可表示为P=s₁Δs₂Δs₃…Δs_k。s₁~s_k都是非空状态，表示为形如〈属性，值〉的元素集合；k表示模式P的长度。给定周期性通配符Δ=[G, G]，模式可以缩写为P=s₁Δs₂…s_k。

通配符Δ=[G, G]是模式P上任意两个相邻状态之间的区间约束，其中，G和G分别表示最小和最大区间约束。即是说，相邻状态之间的最小间隔为G，而最大间隔为G。

定义3^[20]  给定两个状态转移模式P=s₁Δs₂…s_i，P′=s′₁Δs′₂…s′_j，i, j≥1，它的增长操作是P⊗P′=s₁Δs₂…s_iΔs₁′Δs₂′…s_j′。

定义4^[20]  给定$ D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right)$，Δ=[G, G]，以及P=s₁Δs₂…s_k，I=i₁Δi₂…i_k被称为一个位置序列当且仅当

1) 1≤i₁≤|T|; 2) ∀1≤j≤k-1, G≤i_j+1-i_j+1≤G。

条件1)是为了确保I的位置在i₁索引范围内，其他位置没有这个要求。条件2)确保满足间隙约束，也就是说s_j+1应该出现在[G+i_j+1, G+i_j+1]中。

定义5^[20]  给定多元时序数据$ D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right)$，通配符区间Δ=[G, G]，状态转移序列模式P=s₁Δs₂…s_k，位置序列I=i₁Δi₂…i_k。在I上模式P对DB的匹配是一个布尔函数

$ m\left( {DB,I,P} \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{若\;\forall 1 \le j \le k,状态\;{s_j}\;在时间\;{t_{{i_j}}}\;上发生;}\\ {0,}&{其他。} \end{array}} \right. $

定义6^[20]  给定一个时序数据$ D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right)$，一个长度为k的状态转移模式P，P在DB上所有可能出现的次数是|E|=|T|×(G－G+1)^k－1，与P匹配的位置序列集合为E^p={I∈E|m(DB, I, P)=1}，

其中|E^P|表示模式P在DB上出现的次数。因此，P在DB上的支持度是

$ sup \left( {P,DB} \right) = \left( {\left| {{E^P}} \right|/\left| E \right|} \right) \in \left[ {0,1} \right]。$

当时间序列DB给定时，可以简写成sup(P)。由此可给出频繁STAP的定义。

定义7^[20]  给定阈值ρ_d，频繁STAP的集合为

$ F = \left\{ {\forall P \in F\left| {sup \left( P \right) \ge {\rho _d}} \right.} \right\}。$

2 本文算法

本节首先提出STAP的增量挖掘问题并分析其时间复杂度。其次，提出了解决该问题的三支增量模型。然后，基于模型提出了3IU-STAP算法设计与实现。

2.1 问题描述

问题：增量挖掘频繁STAP。

输入：$D B=\left(T, A, V=\bigcup\limits_{a \in A} V_{a}, f\right), d b=\left(T^{*}, A, V=\bigcup\limits_{a \in A} V_{a}, f\right) $, Δ=[G, G], ρ_w, ρ_d, F_DB, W。

输出：F_DB∪db={|P|sup(s∈P, DB∪db)≥ρ_w, sup(P, DB∪db)≥ρ_d}。F_DB∪db是在更新后的数据集上所有满足阈值ρ_w和ρ_d的频繁STAP的集合。

令|T|=n，|A|=m，则$M=\prod\limits_{a \in A}\left(\left|V_{a}\right|+1\right)-1 $。频繁状态挖掘的时间复杂度是⊙(mnM)。STAP是在一组频繁状态上构建的，STAP的长度k∈[1, n]，这里有$\sum\limits_{k=1}^{n} M^{k} $种可能的STAP。由定义6可知，在匹配中计算次数高达mn|Δ|^k-1次。因此，频繁STAP增量挖掘算法的时间复杂度是

$ \odot \left( {\sum\limits_{k = 1}^n m n{{\left| \Delta \right|}^{k - 1}}{{\left( M \right)}^k} + mnM} \right) = \odot \left( {m{n^2}{{\left| \Delta \right|}^n}{{\left( M \right)}^{n + 1}}} \right)。$

虽然问题的时间复杂度是指数级的，但可通过引理1描述的向下封闭性质来大大减少实际运行时间。

引理1  假设ρ_d是STAP的序列阈值。如果P⊆P′，则sup(P′)≤sup(P)。

2.2 3IU-STAP算法 2.2.1 三支增量模型

对于任意给定的候选模式P (由定义3可得)以及支持度，根据它在原始数据DB和增补数据db′上是否频繁，提出了判断候选模式是否频繁的三支划分模型，如式(1)所示，

$ \left\{ \begin{array}{l} P \in POS,\mathit{sup}\left( {P,DB} \right) \ge {\rho _d}\;及\;\mathit{sup}\left( {P,db'} \right) \ge {\rho _d},\\ P \in {\rm{NEG}},\mathit{sup}\left( {P,DB} \right) < {\rho _d}\;及\;\mathit{sup}\left( {P,db'} \right) < {\rho _d},\\ P \in {\rm{BND}},其他。\end{array} \right. $

(1)

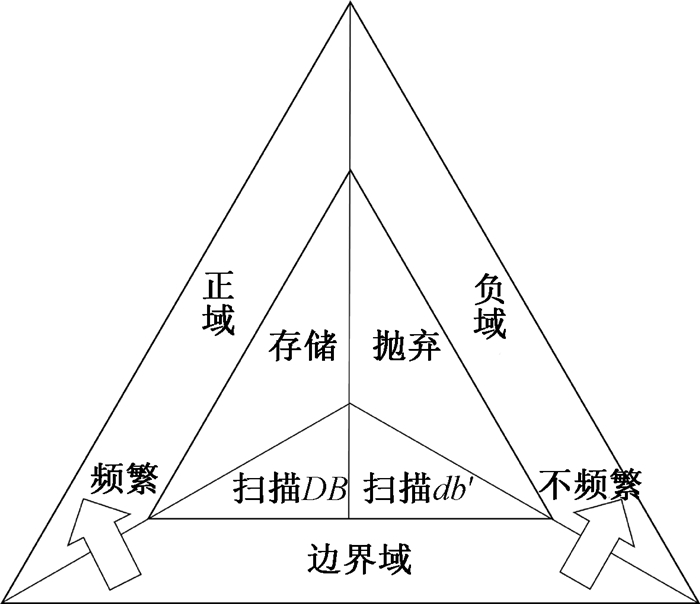
图 1给出了针对这3个区域的处理技术。正域中的候选模式P一定是频繁的，直接接受并存储。负域中的候选模式P一定是不频繁的，直接拒绝并抛弃。边界域中的模式P需要延迟决策，即扫描数据集计算最新的支持度。当一个候选STAP在DB上频繁，而在db′上不频繁，即sup(P, DB)≥ρ_d且sup(P, db′) < ρ_d，扫描db′；当该模式在DB上不频繁，而在db′上频繁，即sup(P, DB) < ρ_d且sup(P, db′)≥ρ_d，扫描DB。

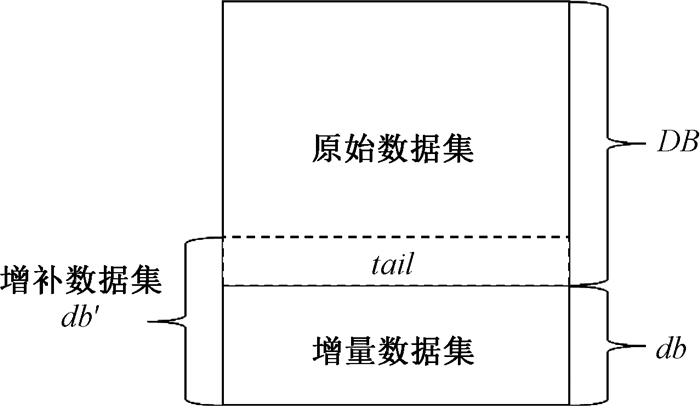
如图 2所示，增补数据集db′由原始数据DB的尾部与增量数据db链接而来，它能保证算法得到准确的STAP挖掘结果。当db被插入时，在DB与db的链接部分会产生额外的序列信息。如果将其遗漏，某些STAP的支持度会变小。对于给定长度为k的任意状态转移模式P=s₁Δs₂…s_k，复制DB尾部一段数据tail，长度为|tail|=(k-1)·(G+1)。因此，STAP的支持度为

$ sup \left( {P,db'} \right) = \left( {\left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right|} \right)/\left| {{E_{db}}} \right|, $

其中：序列集合E_db′^P表示在db′上匹配模式P的位置序列；|E_tail^P|表示tail中模式P已出现的位置序列个数，由于tail上模式P的个数在DB中已经计算过，因此需将其减去；E_db是P在db上出现的位置序列。

最后，基于式(1)与图 1所示模型导出引理2和引理3，以有效降低算法对数据集的扫描。

引理2  若P是存在于正域中的候选模式，则模式P在DB∪db上频繁。

证明

$ \frac{{\left| {E_{DB}^P} \right|}}{{\left| {{E_{DB}}} \right|}} \ge {\rho _d};\frac{{\left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right|}}{{\left| {{E_{db}}} \right|}} \ge {\rho _d}, $

(2)

由于|E_DB|>0且|E_db|>0, 则有

$ \left| {E_{DB}^P} \right| \ge {\rho _d} \cdot \left| {{E_{DB}}} \right|, $

(3)

$ \left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right| \ge {\rho _d} \cdot \left| {{E_{db}}} \right|。$

(4)

不等式同号可相加，由式(3)+式(4)得

$ \left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right| + \left| {E_{DB}^P} \right| \ge {\rho _d} \cdot \left| {{E_{DB}}} \right| + {\rho _d} \cdot \left| {{E_{db}}} \right|。$

(5)

则可得到

$ sup \left( {P,DB \cup db} \right) = \frac{{\left| {E_{DB}^P} \right| + \left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right|}}{{\left| {{E_{DB}}} \right| + \left| {{E_{db}}} \right|}} = \frac{{\left| {E_{DB}^P} \right| + \left| {E_{db'}^P} \right| - \left| {E_{tail}^P} \right|}}{{\left| {{E_{DB \cup db}}} \right|}} \ge {\rho _d}。$

因此P在DB∪db上频繁。

引理3  若P是存在于负域中的候选模式，则模式P在DB∪db上不频繁。

证明  与引理2同理。

2.2.2 算法描述

算法1给出了频繁状态转移模式三支增量挖掘算法的伪代码实现。其输入由7部分组成，即原始数据DB及其频繁状态集W和频繁STAP集F_DB、增量数据db、通配符区间Δ、以及两种阈值ρ_w和ρ_d，ρ_w被用于判断一个状态是否频繁，ρ_d被用于判断一个STAP是否频繁。其输出为更新后的数据集DB∪db上的频繁STAP集合F_DB∪db。

算法1  状态转移模式三支增量挖掘。

输入：DB，db，ρ_d，ρ_w，Δ，F_DB，W;

输出：F_DB∪db。//最新的频繁STAP

方法名：3IU-STAP

1.根据W, DB, db以及ρ_w增量更新频繁状态集，记为W^*;

2.初始化1-F_DB∪db←{ssup(s)≥ρ_d≥ρ_w}⊆W^*, k←2, F_DB∪db←∅;

3. while ((k-1)-F_DB∪db≠∅) do

4.   k-F_DB∪db←∅;//正域中所有长度为k的STAP集合

5.   根据tail和db构造增补数据db′; //将tail作为db的头部

6.   构建候选模式集k-O=(k－1)-F_DB∪db⊗1-F_DB∪db; //笛卡尔积

7.   for each P∈k-O do

8.     if sup(P，db′)≥ρ_d then

9.       if P∈F_DB then k-F_DB∪db=k-F_DB∪db∪{P}; //将频繁模式P存入正域

10.         else isFrequent=delayDecision(DB, P, ρ_d, Δ); //扫描DB，返回布尔值

11.         if isFrequent then k-F_DB∪db=k-F_DB∪db∪{P};

12.       else //在db′上不频繁

13.         if P∈F_DB then isFrequent=delayDecision(db′, P, ρ_d, Δ); //扫描db′，返回布尔值

14.           if isFrequent then k-F_DB∪db=k-F_DB∪db∪{P};

15.         else continue; //此时P属于负域，一定不频繁，直接抛弃

16. return F_DB∪db。

第6行描述了两个频繁STAP集合的笛卡尔积。对任意模式P∈(k－1)-F_DB∪db以及P′∈1-F_DB∪db，长度为k的候选模式通过P⊗P′获得。第8~9行组成的条件对应了式(1)中正域判定条件，其候选STAP属于正域可直接存储。第12、15行对应了式(1)中负域划分条件直接抛弃。第10~11行及13~14行分别描述了两种延迟决策技术。

算法2实现了delayDecision方法以重新扫描DB并获得新的支持度信息。如果这个新支持度不小于指定阈值ρ_d，则再将其划入正域，否则抛弃。

算法2  扫描数据集以更新支持度。

输入：DB, P=s₁Δ₂…s_k, ρ_d, Δ=[G, G];

输出：TRUE or FALSE。

方法名：delayDecision

1. occ=0;

2. for i=1;i < T－k; i++ do

3.   if s₁匹配t_i then occ=occ+count(DB, P, G, G, α←1, β←2); //算法3

4.   if sup(P)=occ/(|T|×(G－G+1)^k－1)≥ρ_d then return TRUE;

5. else return FALSE。

算法3实现了方法count。其中α表示匹配到了DB中第α个时间点，β表示匹配到了模式P中第β个状态。

算法3  统计以t_i开头的所有匹配次数。

输入：DB, P=s₁Δs₂…s_k, ρ_d, Δ=[G, G]，α，β;

输出：occ。

方法名：count

1. if β等于k then return 1; //P中所有的状态都完成了一次匹配

2. occ=0;

3. for i=α+G+1;i≤α+G且α+i≤T; it+do

4.   if s_β匹配t_α+i then occ=occ+count(DB, P, G, G, α+1, β+1);

5. return occ。

3 实验

本章节通过实验对两方面展开了讨论：1) 3IU-STAP性能与频繁阈值ρ_d的关系；2) 3IU-STAP性能与增量大小的关系。

3.1 数据集与预处理

实验环境为CPU：i5-7500 3.40 GHz；内存6 GB；操作系统：Windows 10；IDE：Eclipse，Java。

表 1展示了数据集的基本信息。依次来自UCI、全国数学建模比赛(半开放)、中国海洋石油公司(油井维护数据)。采用的离散化方案参见文献[20]。

3.2 结果分析

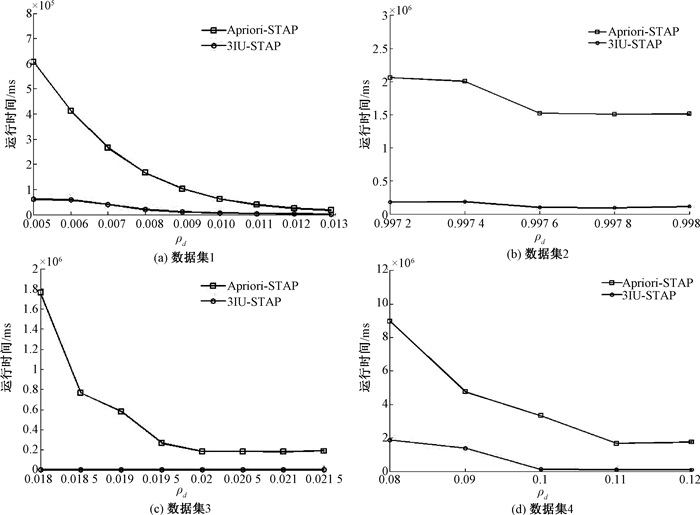
如图 3所示，在各数据集中，增量算法分别比批量算法快7.7倍、12倍、649倍、5.3倍。其中，Δ=[3, 6]，增量划分比例为10%，Apriori-STAP是批量算法。

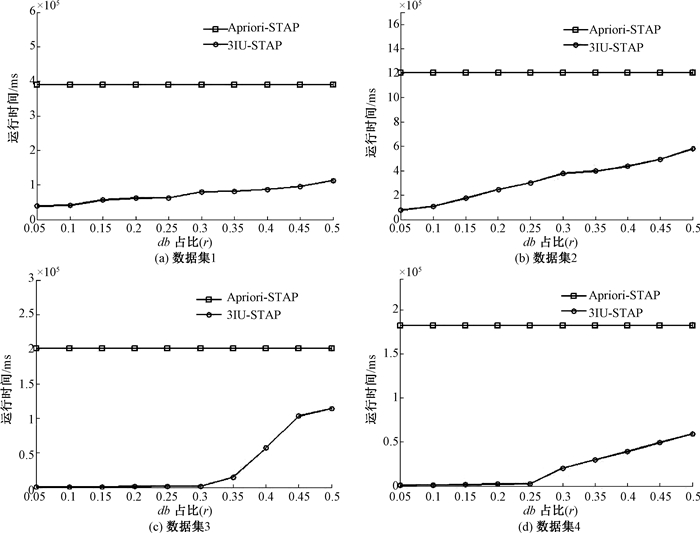
图 4为基于不同增量数据划分比例(r)的算法性能表现。当划分比例较小时，运行时间少。随着r的增加，运行时间增加。因为增量越大，边界域所耗费的时间越大。

4 结论

本文基于三支决策理论，提出了一种多元时序数据上状态转移模式的三支增量模型与挖掘算法3IU-STAP。在插入增量数据时，通过三支划分模型将大量的候选模式划分为正域和负域，从而减少扫描数据集的次数。通过构造增补数据集来确保扫描结果的完备性。理论分析与大量实验结果表明，3IU-STAP能准确高效地获得结果。