2. 河北大学 电子信息工程学院 河北 保定 071002;
3. 河北大学 信息技术中心 河北 保定 071002
2. School of Electronic Information Engineering, Hebei University, Baoding 071002, China;
3. Center for Information Technology, Hebei University, Baoding 071002, China
随着“互联网+”的提出,互联网数据呈爆炸式增长.为了满足科学研究的需求,要应用统计、情报检索、机器学习等方法对数据进行分析挖掘.为避免社会成员之间交互隐私的泄露,在社会网络数据发布前须对数据进行处理,从而达到隐私保护的目的.数据发布中的隐私保护问题已成为网络空间安全领域的热门研究.
现有的隐私保护关键技术主要有匿名化技术、数据加密技术、差分隐私技术、隐私信息检索技术、问责系统以及基于聚类和图修改的隐私保护技术等[1].Terzi等人[2]把节点的度作为攻击者的背景知识,提出了k-度匿名来阻止节点的再识别攻击.Zou等人[3]提出k-自同构的匿名方法.Cheng等人[4]提出了k-同构隐私保护模型.Wang等人[5]将加权网络中的最短路径作为隐私,设计了k-路径匿名模型,以实现最短路径的隐私保护.兰丽辉等人[6]提出了一种基于差分隐私模型的随机扰动方法,设计了LWSPA算法,来实现边和边权重的强保护.张伟等人[7]提出一种基于层次随机图,并且满足ε-差分隐私的社会网络数据发布算法.陈春玲等人[8]将隐私保护级别分级,通过k-分组、(k,Δd)的方法对节点进行匿名,降低了社会网络图的信息损失.Sala A等人[9]对无权社会网络图采用dK-图模型抓取其结构信息,设计基于差分隐私的dK-干扰算法,该算法针对捕获的信息添加拉普拉斯噪声,使得隐私保护后的网络图与原始社会图的结构基本相似.
隐私保护问题的关键是如何在较好的隐私保护程度下,使网络图的信息损失最小、数据集的效用性最高.本文的主要贡献如下:
1) 提出了一种基于马尔科夫算法的社会网络差分隐私数据发布方法.
2) 设计实现了满足ε-差分隐私的MDPA算法,通过向聚好类的节点所在边的权重中,注入服从拉普拉斯分布的噪声来实现隐私保护.
3) 在图形化处理软件Gephi上生成的社会网络图及真实社会网络数据集上进行实验,实验结果验证了MDPA算法满足用户在社会网络中的差分隐私要求,并提高了数据效用性.
1 基本概念 1.1 社会网络图社会网络[10]是指社会个体之间由于互动而形成的相对稳定的体系关系,社会网络是由许多节点构成的社会结构,节点通常指的是个人或组织,权重值代表了个人或组织之间的紧密互动程度.文中的社会网络图采用无向图.图是一种由节点集合以及节点与节点之间的关系集合组成的数据结构.图的存储结构主要是图中边的存储结构,文中采取邻接矩阵的方法存储.
一个社会网络G:G=(V, E),其中:V={x|x∈社会网络的社会个体集合};E={(x, y)|x, y∈V}为社会个体间的互动关系,(x, y)表示从x到y的一条双向通路,即(x, y)是无方向的,也就是说顶点x和顶点y之间存在一条边,x和y互为邻接点,称边(x, y)和顶点x、y相关联.
1.2 马尔科夫算法-MCL马尔科夫聚类算法(MCL)[11]是由Dongen提出的一种典型的快速图形聚类算法.马尔科夫聚类算法的核心步骤是扩展和膨胀.MCL算法流程如下所示.
输入:无向社会网络图G,扩展参数e,膨胀参数p.
输出:聚类结果集V,簇数m.
1) 导出无向图G.
2) 创建G的邻接矩阵.
3) 对每个节点即对角线的每个顶点循环并自加1.
4) 标准化该邻接矩阵(每个元素除以所在列的所有元素之和).
5) 以扩展参数e对邻接矩阵进行扩展(计算矩阵的第e次幂).
6) 用参数p对求得的矩阵进行膨胀处理.
7) 重复步骤5)和6), 直到达到收敛.
8) 得到簇的结果.
本文将图的马尔科夫聚类算法应用到社会网络数据发布的隐私保护中.图聚类的目的是把大型复杂图聚类成不同的簇,然后针对分好的具有相似特征的簇添加噪声.
1.3 差分隐私差分隐私的目的是提供一种在数据库中能最大限度地提高查询准确性,同时又能最大限度地减少识别确定数据的机会.差分隐私保护[12-13]是一种基于数据失真的隐私保护技术,定义了一个极为严格和健壮的保护模型,其基本思想是使用添加噪声的技术达到隐私保护的目的.
定义1 ε-差分隐私(ε-differential privacy).给定两个数据集D和D′,D和D′之间最多相差一条记录,给定一个隐私算法M,Range(M)是M的取值范围,若算法M在数据集D和D′上的任意输出结果S(S∈Range(M))满足不等式,Pr[M(D)∈S]≤eεPr[M(D′)∈S],则称M满足ε-差分隐私.
定义2 敏感度. Δq是查询函数的敏感度,其定义为Δq=maxD1, D2|q(D1)-q(D2)|.
数据集D1、D2之间至多相差一个元素.设两个社会网络数据集G1、G2中,节点相同,有且仅有一条边不同,即全局敏感度设为差异边存在的最大差异权重Δf=Wmax.
差分隐私保护的实现机制有拉普拉斯机制[14]和指数机制[15].拉普拉斯机制适用于结果是数值型的情况,指数机制适用于结果是非数值型的情况.文中采用的是拉普拉斯机制.
定义3 拉普拉斯分布[15].记位置参数μ为0,尺度参数b的拉普拉斯分布为Lap(b),其概率密度函数为:
| $ p\left( x \right) = \frac{1}{{2b}}{\rm{exp}}\left( { - \frac{{\left| x \right|}}{b}} \right), $ | (1) |
| $ A\left( D \right) = Q\left( D \right) + \left\langle {La{p_1}(\frac{{\Delta f}}{\varepsilon }), \cdots, La{p_d}(\frac{{\Delta f}}{\varepsilon })} \right\rangle . $ | (2) |
拉普拉斯机制:对于任何函数Q:D→Rd, 如果算法A的输出结果满足式(2),表明A满足ε-差分隐私.
其中
社会网络图的信息包含两个部分:网络图中的节点信息;描述节点与节点之间关系的边的信息.社会网络的存储结构主要是图中边的存储结构,存储边信息主要有邻接矩阵和邻接表两种方法.本文采用的是邻接矩阵的方式,矩阵元素表示节点间的相互关系.
2.1 MDPA算法基本思想针对社会网络数据发布的隐私保护问题,将图的马尔科夫聚类算法应用到社会网络数据发布的隐私保护中.提出了一种基于马尔科夫聚类算法的社会网络差分隐私数据发布方法MDPA.图聚类的目的是把大型复杂图的节点拆分成不同的簇,然后针对分好的簇的节点和边添加噪声,MDPA算法满足ε-差分隐私模型.为减少拉普拉斯噪声的添加,避免大的误差,采用随机抽样的方式,以Si为抽样频率,对网络边权重添加噪声.
2.2 MDPA算法基本流程MDPA算法步骤如下.
输入:原始网络图G, 隐私保护预算ε, 扩展参数e, 膨胀参数p.
输出:隐私保护后图G*.
1) 创建G的邻接矩阵m.
2) 对邻接矩阵m中的每个节点即对角线的每个顶点循环并自加1.
3) 标准化邻接矩阵m, 矩阵中的元素均除以其对应元素所在列的所有元素的和.
4) 以扩展参数e对邻接矩阵m进行扩展.
5) 用膨胀参数p对求得的矩阵进行膨胀处理.
6) 重复步骤4)和5), 直到达到收敛.
7) 得到节点簇的聚类结果集V, 以及簇数n.
8) 如果网络图是无权图,将随机生成的范围为[1-a]的整数赋值给网络边,作为网络边的权重,生成带权矩阵C.
9) 记录每一个聚类集V的权重信息,将这些权重信息按照聚类集的顺序构成三元组(i, j, x), i, j是节点编号,x代表边的权重,当节点间无边连接时,x设为0.
10)生成X ={x1, x2, …, xm×(m-1)/2}.
11)对X以Si为频率进行随机抽样(Si=抽样个数/ X向量总权重数),生成满足ε-差分隐私的拉普拉斯噪声,Lap=ddlaplace(m, n, μ, b).
12)构造长度为d的服从Laplace分布的向量<Lap(Δf/ε)>X.
13)生成满足ε-差分隐私的G*的向量MDPA(G)= Pi= X +Lap(Δf/ε)X.
14)发布G的隐私保护图G*.
2.3 算法隐私性分析根据差分隐私的定义,给定两个社会网络图数据集G1和G2,G1和G2之间至多相差一条记录,设G1和G2节点相同,有且仅有一条边不同,给定一个隐私算法MDPA,Range(MDPA)是MDPA的取值范围,若算法MDPA在数据集G1和G2上的任意输出结果P(P ∈Range(MDPA))满足如下不等式,则MDPA算法满足ε-差分隐私.
| $ {\rm{Pr}}\left[{\mathit{MDPA}\left( {\mathit{G}1} \right) \in \mathit{\boldsymbol{P}}} \right] \le {{\rm{e}}^\varepsilon }{\rm{Pr}}\left[{\mathit{MDPA}\left( {\mathit{G}2} \right) \in \mathit{\boldsymbol{P}}} \right]. $ | (3) |
证明 设p∈ P,P与X维度相同,由条件概率可知
Pr[MDPA(G1)=p]/Pr[MDPA(G2)=p]=
由(X(G1)-X(G2))≤Wmax知
| $ \begin{array}{l} {\rm{exp}}\left\{ {\left( {X\left( {G1} \right) - X\left( {G2} \right)} \right)/({W_{{\rm{max}}}}/\varepsilon )} \right\} \le {\rm{exp}}\left\{ {{W_{{\rm{max}}}}/({W_{{\rm{max}}}}/\varepsilon )} \right\} = \\ {\rm{exp}}\left\{ \varepsilon \right\} = {{\rm{e}}^\varepsilon } \Rightarrow ({\rm{Pr}}\left[{\mathit{MDPA}\left( {\mathit{G}1} \right) = \mathit{p}} \right]/{\rm{Pr}}\left[{\mathit{MDPA}\left( {\mathit{G}2} \right) = \mathit{p}} \right]) \le {{\rm{e}}^\varepsilon }. \end{array} $ |
因为p∈ P, 所以Pr[MDPA(G1)∈ P]/Pr[MDPA(G2)∈ P]≤eε.
3 实验及分析 3.1 实验设置实验环境是:Intel(R) Core(TM) i5-4590 CPU@3.30 GHz 4.00 GB内存,操作系统是Microsoft Windows 7旗舰版,编程语言是C+ +和Matlab.
实验数据如表 1所示.Lesmis是带权社会网络图.Social Net、Karate和American CF网络是无权图,利用随机数生成器为其边权重随机生成区间在[1, 10]的整数作为边的权重值.
|
|
表 1 实验数据 Table 1 Experimental data |
实验测试了MDPA算法在4个社会网络数据集上的执行时间.实验结果均是5次实验取平均值后的结果.如图 1所示.

|
图 1 执行时间 Figure 1 Execution time |
实验的目的是测试随着隐私预算参数ε、马尔科夫聚类算法阶段的膨胀参数p的取值变化,对MDPA算法执行时间的影响.图 1(a)~1(c)的p值分别为2、4、8,ε分别取值0.05、0.1、1、10.由实验结果可知,当p值一定时,随着ε的增大,MDPA算法的执行时间受ε的影响较小.比较ε取值确定的情况下,随着p取值的增大,网络图聚类数增多,执行时间会稍微增大.当社会网络图的数据集规模越来越大时,执行时间会增加,实验结果表明,执行时间主要受数据集中节点以及边的数量的影响.
3.2.2 数据效用分析实验测试了MDPA算法在4个社会网络数据集上的数据效用性.实验从两个方面(平均最短路径、平均聚类系数)测试MDPA算法的效用性.实验结果均是5次实验取平均值后的结果.
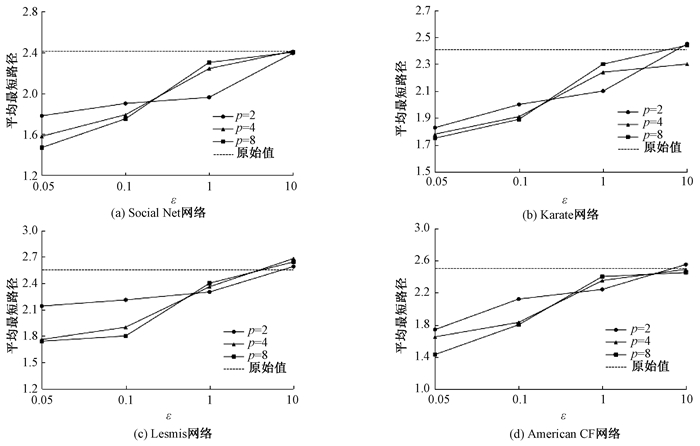
平均最短路径的实验分析情况如图 2所示.实验的目的是测试随着隐私预算参数ε、马尔科夫聚类算法阶段的膨胀参数p的取值变化,对平均最短路径ASPL值的影响.由图 2可知,当p值一定的情况下,随着ε的增大,隐私保护程度降低,相应数据效用会越高,平均最短路径ASPL越发接近隐私保护前网络图的原始ASPL值,验证了理论上,ε越大数据的效用性越高.当ε值一定的情况下,并且当ε达到一定的值,趋向于1或大于1时,随着p的增加,网络图聚类数增多,ASPL的值与初始社会网络图的差异越来越小,数据效用性越高.
|
图 2 平均最短路径 Figure 2 Average shortest path |
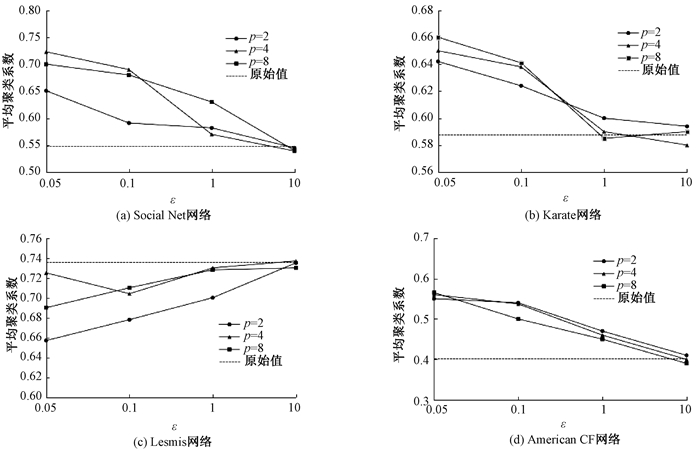
平均聚类系数的实验分析情况如图 3所示.
|
图 3 平均聚类系数 Figure 3 Average clustering coefficient |
实验的目的是测试随着隐私预算参数ε、马尔科夫聚类算法阶段的膨胀参数p的取值变化,对平均聚类系数ACC值的影响.由图 3可知,当p值一定的情况下,随着ε的增大,隐私保护程度降低,相应数据效用增高,平均聚类系数ACC越发接近隐私保护前网络图的原始ACC值.当ε值一定的情况下,并且当ε达到一定的值,趋向于1或大于1时,随着p的增加,网络图聚类数增多,ACC的值与初始社会网络图的差异越来越小,数据效用性越高.
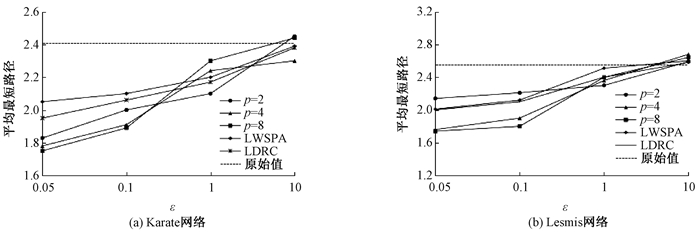
3.2.3 实验对比实验选取LWSPA算法[5]和LDRC算法[8]与MDPA算法在Karate和Lesmis社会网络数据集上进行实验比较,实验结果如图 4和图 5所示.
|
图 4 平均最短路径对比试验 Figure 4 The comparison test of average shortest path |
|
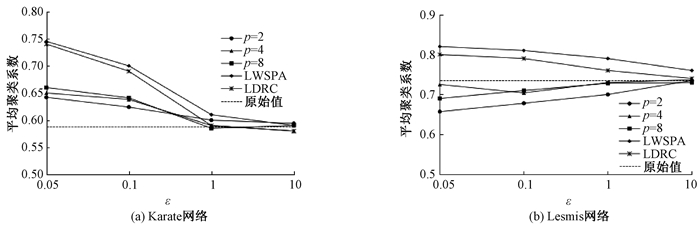
图 5 平均聚类系数对比试验 Figure 5 The comparison test of average clustering coefficient |
由图 4(a)和图 4(b)可知,随着ε的增大,MDPA算法中,当p为4、8时,平均最短路径的值更接近于初始网络,数据有效性优于LWSPA算法和LDRC算法.由图 5(a)和图 5(b)可知,数据有效性明显优于LWSPA算法和LDRC算法.随着ε的增大,数据的平均最短路径值和平均聚类系数值会趋近于原始社会网络图.实验证明了MDPA算法相比较于LWSPA算法和LDRC算法具有明显的优越性.
4 结论针对社会网络中数据发布面临的隐私保护问题,在严格的ε-差分隐私模型下,提出了一种基于马尔科夫算法的社会网络差分隐私数据发布MDPA算法.将图的MCL聚类算法应用到社会网络数据发布的隐私保护中.MDPA以Si为抽样频率,对网络边权重添加满足ε隐私保护预算,服从拉普拉斯分布的噪声,有效降低了数据集的误差,提高了数据的效用性.
| [1] |
曾庆山, 张贵勇. 基于距离阈值的自适应K-均值聚类算法[J]. 郑州大学学报(理学版), 2016, 48(4): 90-94. (  0) 0) |
| [2] |
LIU K, TERZI E. Towards identity anonymization on graphs[C]// ACM SIGMOD International Conference on Management of Data. Vancouver, 2008: 93-106.
(  0) 0) |
| [3] |
ZOU L, CHEN L, ZSU M T. K-automorphism: a general framework for privacy preserving network publication[J]. Proceedings of the vldb endowment, 2009, 2(1): 946-957. DOI:10.14778/1687627 (  0) 0) |
| [4] |
CHENG J, FU W C, LIU J. K-isomorphism: privacy preserving network publication against structural attacks[C]// ACM SIGMOD International Conference on Management of Data. Indianapolis, 2010: 459-470.
(  0) 0) |
| [5] |
WANG S L, TSAI Z Z, HONG T P, et al. Anonymizing shortest paths on social network graphs[J]. Lecture notes in computer science, 2011, 6591(3): 129-136. (  0) 0) |
| [6] |
兰丽辉, 鞠时光. 基于差分隐私的权重社会网络隐私保护[J]. 通信学报, 2015, 36(9): 145-159. DOI:10.11959/j.issn.1000-436x.2015165 (  0) 0) |
| [7] |
张伟, 仓基云, 王旭然, 等. 基于层次随机图的社会网络差分隐私数据发布[J]. 南京邮电大学学报(自然科学版), 2016, 36(3): 23-32. (  0) 0) |
| [8] |
陈春玲, 熊晶, 陈琳, 等. 基于动态社会网络数据发布的个性化隐私保护[J]. 南京邮电大学学报(自然科学版), 2016, 36(2): 74-81. (  0) 0) |
| [9] |
SALA A, ZHAO X, WILSON C, et al. Sharing graphs using differentially private graph models[C]// ACM SIGCOMM Conference on Internet Measurement Conference. Berlin, 2011: 81-98.
(  0) 0) |
| [10] |
兰丽辉. 基于向量模型的加权社会网络发布隐私保护方法研究[D]. 镇江: 江苏大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10299-1015621813.htm
(  0) 0) |
| [11] |
杨楠, 林松祥, 高强, 孟小峰. 一种从马尔可夫聚类簇发现潜在WEB社区特征的方法[J]. 计算机学报, 2007, 30(7): 1086-1093. (  0) 0) |
| [12] |
DWORK C. Differential privacy: a survey of results[C]// International Conference on Theory and Applications of MODELS of Computation. Berlin, 2008: 1-19.
(  0) 0) |
| [13] |
熊平, 朱天清, 王晓峰. 差分隐私保护及其应用[J]. 计算机学报, 2014, 37(1): 101-122. (  0) 0) |
| [14] |
DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[C]// Proceeding of the 3rd Conference on Theory of Cryptography. New York, 2006: 265-284.
(  0) 0) |
| [15] |
MCSHERRY F, TALWAR K. Mechanism design via differential Privacy[C]//Proceeding of the 48th Annual IEEE Symposium on Foundations of Computer Science. Providence, 2007: 94-103.
(  0) 0) |
| [16] |
ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of anthropological research, 1977, 33(4): 452-473. DOI:10.1086/jar.33.4.3629752 (  0) 0) |
| [17] |
KNUTH D E. The stanford graph Base: a Platform for combinatorial computing[M]. New York: ACM Press, 1994.
(  0) 0) |
| [18] |
GIRVAN M, NEWMAN E J. Community structure in social and biological networks[J]. Proceedings of the national academy of sciences of the united states of america, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


