在诸如自动化生产线、机械臂、工业机械手等自动化过程的跟踪控制中,无法跟踪全部数据点,只能在某些特定的数据点上进行有效检测。因此,针对这些特定数据点进行高精度的点到点跟踪控制研究具有重要的实际意义。
最早的点到点跟踪问题主要集中于研究一类终点跟踪问题,点对点跟踪控制问题的解决思路是:设计一条经过特定跟踪点的轨迹,把问题转化为一般的全轨迹跟踪问题。这种方法主要关心跟踪轨迹的设计。文献[1]提出了终端迭代学习控制算法来解决列车进站问题。文献[2-3]提出了一种基于优化跟踪误差的方法来直接得到输入,该方法的优势在于不需要设计初始轨迹,但是并没有给出解决方案来克服外界干扰。针对有初始状态扰动的点到点跟踪控制问题,文献[4]提出一种基于插值法轨迹更新的P型闭环迭代学习控制算法,算法的跟踪性能有了很大的改善,但并没有考虑算法的优化问题,进而提升算法的收敛速度和跟踪精度。文献[5]针对非线性扰动作用的离散线性系统的输出跟踪控制问题,提出了基于参考轨迹更新的点到点迭代学习控制算法,在控制律的设计中引入范数优化思想,讨论了无扰动和非重复扰动情形下算法的收敛性和鲁棒性。但是文献[5]仅利用当前次迭代得到的信息,没有利用以前多次迭代过程中得到的信息来提高算法的跟踪性能。文献[6-7]指出在算法稳定的前提下,指数变增益学习律能有效提高算法的学习效率和收敛速度。因此,在进行目标轨迹更新过程中,将固定的学习增益λ改为随迭代变化的指数变增益eγ(k),一方面能够克服固定学习增益选取的盲目性,另一方面还能有效提高更新速度、减少算法的运行时间。文献[8-13]采用范数优化的思想,将点到点跟踪与优化思想结合,充分利用点到点跟踪中的额外自由度,从而实现需求的性能指标。文献[14]针对线性时不变离散系统的跟踪问题,提出一种高阶参数迭代学习控制算法,利用了以前多次迭代过程的输入、输出信息来构造新的控制输入,可有效提高算法沿迭代方向的收敛速度和鲁棒性。
在迭代学习控制中,高阶算法能够削弱系统噪声和外界干扰对跟踪性能的影响,从而能够快速、高精度地跟踪控制。与范数优化理论相比,迭代学习控制参数优化技术在工程上更容易实现。因此,为解决点到点跟踪控制中存在的参考轨迹更新速度慢、跟踪精度低、学习速度慢、鲁棒性低等问题,本文提出一种快速参考轨迹更新的点到点二阶参数优化迭代学习控制算法。在进行参考轨迹更新的过程中,将固定更新增益λ改为随迭代变化的指数变增益eγ(k),目的是使新的参考轨迹快速逼近系统输出。在控制律的设计中,尽可能多地利用迭代过程中得到的输入、输出信息,从而实现目标点的实际输出快速、高精度地跟踪期望输出,并提高算法的鲁棒性。
1 问题描述分析考虑如下的单输入、输出离散线性时不变系统中某些特定点的跟踪控制问题
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k}\left( {t + 1} \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_k}\left( t \right) + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{u}}_k}\left( t \right)}\\ {{\mathit{\boldsymbol{y}}_k}\left( t \right) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k}\left( t \right)} \end{array}} \right., $ | (1) |
其中:CB≠0;k表示迭代次数;t∈[0, T]表示系统采样时间区间;xk(t)∈Rm, uk(t)∈R, yk(t)∈R分别为系统(1)第k次迭代t时刻的状态、输入及输出变量;A, B, C分别为相应维数的实矩阵。系统(1)的期望输出轨迹为yd(t)∈R;定义ud=[ud(0), ud(1), …, ud(N-1)]T为最优跟踪时的系统输入;定义ek(t)为系统第k次迭代t时刻的跟踪误差,即ek(t)=yd(t)-yk(t)。
将状态空间形式的系统模型(1)转换为基于时间序列的输入、输出形式矩阵模型,等价为
| $ {\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{u}}_k} + \mathit{\boldsymbol{d}}。$ | (2) |
其中G和d分别为
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CB}}}&0&0& \cdots &0\\ {\mathit{\boldsymbol{CAB}}}&{\mathit{\boldsymbol{CB}}}&0& \cdots &0\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^2}\mathit{\boldsymbol{B}}}&{\mathit{\boldsymbol{CAB}}}&{\mathit{\boldsymbol{CB}}}& \cdots &0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 1}}\mathit{\boldsymbol{B}}}& \cdots & \cdots &{\mathit{\boldsymbol{CAB}}}&{\mathit{\boldsymbol{CB}}} \end{array}} \right];\mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CA}}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^2}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^3}}\\ \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 1}}} \end{array}} \right]{\mathit{\boldsymbol{x}}_0}。$ |
定义uk和yk分别为输入和输出的时间序列向量:
| $ {\mathit{\boldsymbol{u}}_k} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_k}\left( 0 \right)}&{{\mathit{\boldsymbol{u}}_k}\left( 1 \right)}& \cdots &{{\mathit{\boldsymbol{u}}_k}\left( {N - 1} \right)} \end{array}} \right]^{\rm{T}}};{\mathit{\boldsymbol{y}}_k} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{y}}_k}\left( 1 \right)}&{{\mathit{\boldsymbol{y}}_k}\left( 2 \right)}& \cdots &{{\mathit{\boldsymbol{y}}_k}\left( N \right)} \end{array}} \right]^{\rm{T}}}。$ |
定义yd和ek分别为期望输出和系统跟踪误差向量:
| $ {\mathit{\boldsymbol{y}}_d} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{y}}_d}\left( 1 \right)}&{{\mathit{\boldsymbol{y}}_d}\left( 2 \right)}& \cdots &{{\mathit{\boldsymbol{y}}_d}\left( N \right)} \end{array}} \right]^{\rm{T}}};{\mathit{\boldsymbol{e}}_k} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_k}\left( 1 \right)}&{{\mathit{\boldsymbol{e}}_k}\left( 2 \right)}& \cdots &{{\mathit{\boldsymbol{e}}_k}\left( N \right)} \end{array}} \right]^{\rm{T}}}。$ |
通常的控制目标在t∈[0, T]中的每一个时间点上,实际输出yk(t)都要逼近期望输出yd(t)。即设计输入控制律uk+1=f(uk, uk-1, …, uk-r, ek, ek-1, …, ek-s),使得
在点到点的跟踪控制中,只要求在某些特定的数据点上实现完全跟踪。因此,可以充分考虑对特定点跟踪控制的自由性,对参考轨迹进行更新,从而减少算法运行时间和提高学习效率。在需要跟踪的特定时间点T={t1, t2, …, ts}处,要求rk(ti)=r0(ti)=yd(ti)。不需要跟踪的时间点处进行参考轨迹更新,使新参考轨迹逐渐逼近系统输出,即‖ rk+1-yk ‖ ≤ ‖ rk-yk ‖。rk+1为第k次更新后的参考轨迹。文献[4]指出可以通过插值法对参考轨迹更新,并设计P型闭环控制律。即
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{k + 1}} = \lambda \cdot \left( {{\mathit{\boldsymbol{r}}_k} - {\mathit{\boldsymbol{y}}_k}} \right)}\\ {{\mathit{\boldsymbol{u}}_{k + 1}} = {\mathit{\boldsymbol{u}}_k} + \mathit{\Gamma }\left( {{\mathit{\boldsymbol{r}}_{k + 1}} - {\mathit{\boldsymbol{y}}_{k + 1}}} \right)} \end{array}} \right.。$ | (3) |
式(3)中λ满足
| $ \left\{ {\begin{array}{*{20}{l}} { - 2 < {\lambda _j}\left( t \right) < 0,t \in \left[ {0,N} \right]\backslash T,j = 1,2, \cdots ,n}\\ {{\lambda _j}\left( t \right) = 0,t \in T,j = 1,2, \cdots ,n} \end{array}} \right.。$ | (4) |
在进行如式(3)的参考轨迹更新过程中,λ和Γ一般选取固定值,因而存在一定的随机性,使得算法存在参考轨迹更新速度慢、运行时间长等问题。为了克服这些问题,考虑将λ改为随迭代变化的指数变增益eγ(k)。参考轨迹更新方法为
| $ {\mathit{\boldsymbol{r}}_{k + 1}} = {\mathit{\boldsymbol{r}}_k} + \left( {{{\rm{e}}^{\gamma \left( k \right)}} - 1} \right) \cdot \left( {{\mathit{\boldsymbol{r}}_k} - {\mathit{\boldsymbol{y}}_k}} \right)。$ | (5) |
定理1 在点到点跟踪问题中,采用如式(5)的参考轨迹更新方法,使‖ rk+1-yk ‖ ≤ ‖ rk-yk ‖成立的充分条件是γ(k)满足
| $ \left\{ {\begin{array}{*{20}{l}} {\gamma \left( k \right) < 0,t \in \left[ {0,N} \right]\backslash T,k = 1,2, \cdots ,n}\\ {\gamma \left( k \right) = 0,t \in T,k = 1,2, \cdots ,n} \end{array}} \right.。$ |
证明 由式(5)可得rk+1-yk=rk-yk+(eγ(k)-1) ·(rk-yk)=eγ(k) ·(rk-yk),‖ rk+1-yk ‖ = ‖ eγ(k) ·(rk-yk) ‖ ≤eγ(k) · ‖ (rk-yk) ‖。
在需要跟踪的时间点t∈{t1, t2, …, ts}处,要求rk(ti)=r0(ti)=yd(ti)。在第k次迭代时若满足γ(k)=0及r0(ti)=yd(ti)时,从而rk+1(ti)=rk(ti)=…=r0(ti)=yd(ti),满足要求。
在不需要跟踪的时间点t∈[0,N]且t∉{t1, t2, …, ts}处,为了让新的参考轨迹快速逼近系统输出,进行参考轨迹更新,并将传统的固定更新增益λ改为随迭代变化的eγ(k)形式。第k次迭代时,在所有不需要跟踪的时间点处,若满足γ(k) < 0时,那么eγ(k) < 1,从而‖ rk+1-yk ‖ ≤ ‖ rk-yk ‖成立。
2.2 点到点二阶参数优化迭代学习控制算法高阶算法利用以前多次迭代的控制输入和跟踪误差进行加权处理,来提高算法的跟踪性能。针对系统(1)的点到点跟踪控制问题,考虑点到点二阶参数优化迭代学习控制算法
| $ {\mathit{\boldsymbol{u}}_{k + 1}}\left( t \right) = {\mathit{\boldsymbol{u}}_k}\left( t \right) + {\mathit{\boldsymbol{\beta }}_{1,k + 1}}\left( t \right){\mathit{\boldsymbol{e}}_k}\left( {t + 1} \right) + {\mathit{\boldsymbol{\beta }}_{2,k + 1}}\left( t \right){\mathit{\boldsymbol{e}}_{k - 1}}\left( {t + 1} \right),t \in T, $ | (6) |
其中:ek(t+1)表示当前次迭代的误差信息;ek-1(t+1)表示上一次迭代得到的误差信息;参数β1, k+1、β2, k+1的目标优化函数为
| $ J = {\left\| {{\mathit{\boldsymbol{e}}_{k + 1}}} \right\|^2} + {w_1} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{1,k + 1}}} \right\|^2} + {w_2} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{2,k + 1}}} \right\|^2},{w_1} > 0,{w_2} > 0, $ | (7) |
其中:β1, k+1=[β1, k+1(0), β1, k+1(1), …, β1, k+1(N-1)]T;β2, k+1=[β2, k+1(0), β2, k+1(1), …, β2, k+1(N-1)]T。
根据系统(1)可得
| $ \begin{array}{l} - \Delta {\mathit{\boldsymbol{e}}_{k + 1}}\left( t \right) = {\mathit{\boldsymbol{e}}_k}\left( t \right) - {\mathit{\boldsymbol{e}}_{k + 1}}\left( t \right) = \mathit{\boldsymbol{C}}\left( {{x_{k + 1}}\left( t \right) - {x_k}\left( t \right)} \right) = \mathit{\boldsymbol{CA}}\Delta {\mathit{\boldsymbol{x}}_{k + 1}}\left( {t - 1} \right) + \\ \mathit{\boldsymbol{CB}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( t \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( t \right)} \right] \cdot {\left[ {{\mathit{\boldsymbol{\beta }}_{1,k + 1}}\left( {t - 1} \right),{\mathit{\boldsymbol{\beta }}_{2,k + 1}}\left( {t - 1} \right)} \right]^{\rm{T}}}, \end{array} $ | (8) |
其中:Δek+1(t)=ek+1(t)-ek(t);Δxk+1(t)=xk+1(t)-xk(t);Δuk+1(t)=uk+1(t)-uk(t)。
式(8)可以转换为
| $ - \Delta {\mathit{\boldsymbol{e}}_{k + 1}} = {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{\beta }}_{k + 1}}, $ | (9) |
其中:βk+1=[β1, k+1(0), β2, k+1(0), β1, k+1(1), β2, k+1(1),…,β1, k+1(N-1), β2, k+1(N-1)]T;
| $ {\mathit{\boldsymbol{G}}_k} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_k}\left( 1 \right)}&0& \cdots &0\\ {\mathit{\boldsymbol{CA}}{\mathit{\boldsymbol{B}}_k}\left( 1 \right)}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_k}\left( 2 \right)}& \cdots &0\\ \vdots & \vdots &{}& \vdots \\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 1}}{\mathit{\boldsymbol{B}}_k}\left( 1 \right)}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 2}}{\mathit{\boldsymbol{B}}_k}\left( 2 \right)}& \cdots &{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_k}\left( N \right)} \end{array}} \right]; \\{\mathit{\boldsymbol{B}}_k}\left( t \right) = \mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( t \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( t \right)} \right];\mathit{\boldsymbol{W}} = {\rm{diag}}\left\{ {{w_1},{w_2}, \cdots ,{w_1},{w_2}} \right\}。$ |
将式(9)代入式(7)可得
| $ J = {\left\| {{\mathit{\boldsymbol{e}}_k} + {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{\beta }}_{k + 1}}} \right\|^2} + {w_1} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{1,k + 1}}} \right\|^2} + {w_2} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{2,k + 1}}} \right\|^2} = {\left\| {{\mathit{\boldsymbol{e}}_k} + {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{\beta }}_{k + 1}}} \right\|^2} + \mathit{\boldsymbol{W}} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{k + 1}}} \right\|^2}。$ | (10) |
通过目标优化函数J对βk+1求偏导,求得每一次迭代时的最优参数β1, k+1和β2, k+1,从而随着迭代的进行,跟踪误差单调快速收敛。通过式(10)对βk+1求偏导得到
| $ \mathit{\boldsymbol{\beta }}_{k + 1}^ * = {\left( {\mathit{\boldsymbol{W}} + \mathit{\boldsymbol{G}}_k^{\rm{T}}{\mathit{\boldsymbol{G}}_k}} \right)^{ - 1}}\mathit{\boldsymbol{G}}_k^{\rm{T}}{\mathit{\boldsymbol{e}}_k}。$ | (11) |
定理2 当采用算法(6)进行点到点跟踪控制时,当迭代次数k→∞时,在待跟踪的时间点t∈{t1, t2, …, ts}处,有‖ ek+1 ‖ < ‖ ek ‖,并且
证明 将非最优解β1, k+1= 0, β2, k+1= 0代入目标函数J得
| $ {\left\| {{\mathit{\boldsymbol{e}}_{k + 1}}} \right\|^2} \le {\left\| {{\mathit{\boldsymbol{e}}_{k + 1}}} \right\|^2} + {w_1} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{1,k + 1}}} \right\|^2} + {w_2} \cdot {\left\| {{\mathit{\boldsymbol{\beta }}_{2,k + 1}}} \right\|^2} \le {\left\| {{\mathit{\boldsymbol{e}}_k}} \right\|^2}。$ | (12) |
用算法(6)进行点到点跟踪控制的过程中,通过式(11)对控制律中的参数进行优化可以保证‖ ek+1 ‖ < ‖ ek ‖。
根据式(12)递推及
| $ \sum\limits_{k = 0}^\infty {\left( {{w_1} \cdot {{\left\| {{\mathit{\boldsymbol{\beta }}_{1,k + 1}}} \right\|}^2} + {w_2} \cdot {{\left\| {{\mathit{\boldsymbol{\beta }}_{2,k + 1}}} \right\|}^2}} \right)} \le {\left\| {{\mathit{\boldsymbol{e}}_0}} \right\|^2}。$ | (13) |
由式(13)可知,序列{w1 · ‖ β1, k+1 ‖2+w2 · ‖ β2, k+1 ‖2}收敛,则
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_k}\left( {{t_i}} \right) = {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}_k}\left( {{t_i}} \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right) + {\left( {\mathit{\boldsymbol{CA}}{\mathit{\boldsymbol{B}}_k}\left( {{t_i}} \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_i} + 1} \right) + \cdots + {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - {t_i}}}{\mathit{\boldsymbol{B}}_k}\left( {{t_i}} \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( N \right) = \\ {\left( {\mathit{\boldsymbol{CB}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right) + {\left( {\mathit{\boldsymbol{CAB}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_i} + 1} \right) + \cdots + \\ {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - {t_i}}}\mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( N \right)。\end{array} $ |
由于在不需要跟踪的点t∈[0,N],且t∉{t1, t2, …, ts}处,满足
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_k}\left( {{t_i}} \right) = {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{t_1} - {t_i}}}\mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_1}} \right) + {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{t_2} - {t_i}}}\mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_2}} \right) + \cdots + \\ {\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{{t_s} - {t_i}}}\mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{e}}_k}\left( {{t_i}} \right),{\mathit{\boldsymbol{e}}_{k - 1}}\left( {{t_i}} \right)} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{e}}_k}\left( {{t_s}} \right)。\end{array} $ |
显而易见,Sk(ts)=(CB[ek(ts), ek-1(ts)])Tek(ts)。由CB≠ 0且
由Sk(ts-1)=(CB[ek(ts-1), ek-1(ts-1)])T ·ek(ts-1)+(CAts-ts-1B[ek(ts-1), ek-1(ts-1)])T ·ek(ts)及
为使参数优化迭代学习控制算法能够应用于非正定系统,并表现出高跟踪性能,算法(6)使用在时间域上时变的学习增益参数βk+1(t),来取代传统参数优化迭代学习控制算法中时不变的参数βk+1。这样设计可以使参数的选取更加灵活自由,由
为提高算法的跟踪性能,并应用于一类离散线性时不变系统的点到点跟踪控制中,考虑算法
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_{k + 1}} = {\mathit{\boldsymbol{r}}_k} + \left( {{\mathit{\boldsymbol{e}}^{\gamma \left( k \right)}} - 1} \right) \cdot \left( {{\mathit{\boldsymbol{r}}_k} - {\mathit{\boldsymbol{y}}_k}} \right)\\ {\mathit{\boldsymbol{u}}_{k + 1}}\left( t \right) = {\mathit{\boldsymbol{u}}_k}\left( t \right) + {\mathit{\boldsymbol{\beta }}_{1,k + 1}}\left( t \right){\mathit{\boldsymbol{e}}_k}\left( t \right) + {\mathit{\boldsymbol{\beta }}_{2,k + 1}}\left( t \right){\mathit{\boldsymbol{e}}_{k - 1}}\left( t \right) \end{array} \right.。$ | (14) |
为使算法表现出高跟踪性能,随迭代变化的指数变增益eγ(k)需要满足定理1;参数β1, k+1、β2, k+1的最优解由式(10)解得。
3 仿真分析为了验证算法的有效性和科学性,考虑如下的电机驱动单机械臂控制系统[5], 其动态模型为
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \frac{N}{{{\psi _t}}}{x_1} - \frac{{{B_c}}}{{{\psi _t}}}{x_2} + \frac{{{K_t}}}{{{\psi _t}}}{x_3}\\ {{\dot x}_3} = - \frac{{{K_b}}}{\mathit{\Gamma }}{x_2} - \frac{{{R_r}}}{\mathit{\Gamma }}{x_3} + \frac{1}{\mathit{\Gamma }}u\\ y = {x_1} \end{array} \right., $ | (15) |
其中:
电机控制系统的实际变量参数分别设定为Kt=1 N ·m、Kb=0.085 V ·s/rad、Rr=0.075 Ω、Bc=0.015 kg ·m2/s、Dc=0.05、l=0.6 m、m1=0.05 kg、m2=0.01 kg、Ξ=0.05 kg ·m2、Γ=0.000 8 Ω、g=9.8 m/s2。系统仿真时间设定为t=2 s,采样时间设定为ts=0.1 s,则系统的离散状态空间表达式的矩阵参数可表示为
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{r}} {1.0207}&{0.0434}&{0.0088}\\ {0.2982}&{0.0765}&{0.0233}\\ { - 0.3286}&{ - 0.1269}&{ - 0.0383} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ \begin{array}{l} 0.665\;5\\ 10.959\;2\\ 1.423\;0 \end{array} \right],\mathit{\boldsymbol{C}} = \left[ {100} \right],\mathit{\boldsymbol{D}} = {\bf{0}}。$ |
从而可以将动态模型(15)转换为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k}\left( {t + 1} \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_k}\left( t \right) + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{U}}_k}\left( t \right)}\\ {{\mathit{\boldsymbol{y}}_k}\left( t \right) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k}\left( t \right) + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{U}}_k}\left( t \right)} \end{array}} \right., $ |
式中:k∈[1, 20];t∈[0, 2]。待跟踪的点为T={0.5, 1, 1.5, 2},期望输出yd(T)={0, 0, 0, 0}。系统(15)的输入输出模型矩阵G+GT的特征值范围在[-3.52 28.64],因此该系统非正定。值得提出的是,算法(14)应用于非正定系统(15)时,仍然能够保证跟踪误差单调收敛。取u0(t)=0.5,β1, k+1、β2, k+1可经参数优化得到。为保证良好的跟踪性能,w1、w2都取10-5。采用算法(14)来解决上述点到点跟踪控制问题,在需要跟踪的点处,取γ(k)=0;在不需要跟踪的点处,随迭代变化的指数变增益取γ(k)=-k。
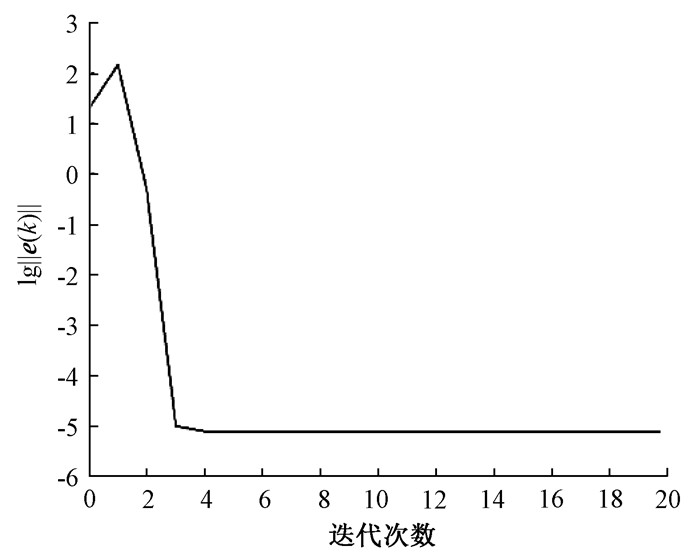
图 1给出了点到点二阶参数优化迭代学习控制算法的系统输出误差范数在迭代域上的收敛情况。从图 1中可以看出,仅仅经过几次迭代,算法(14)就能表现出较好的跟踪性能。
|
图 1 算法(14)对系统(15)的跟踪误差 Fig. 1 Tracking error of system (15) by algorithm (14) |
在实际的工业过程中,很难保证外部干扰等不确定性在每一次试验时都是相同的。因此,考虑存在建模误差ΔG和非重复性外部干扰r时,测试二阶参数优化点到点迭代学习控制算法的鲁棒性。在系统(15)中加入模型误差ΔG和非重复性外部干扰r,则
| $ \Delta \mathit{\boldsymbol{A}} = 0.02 \cdot \left[ {\begin{array}{*{20}{c}} 1&1&1\\ 1&1&1\\ 1&1&1 \end{array}} \right],\Delta \mathit{\boldsymbol{B}} = 0.02 \cdot \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ 1 \end{array}} \right],\Delta \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \end{array}} \right],r = 0.01 \cdot {\rm{rand}}\left( 1 \right),{\rm{rand}}\left( 1 \right) \in \left[ {0,1} \right]。$ |
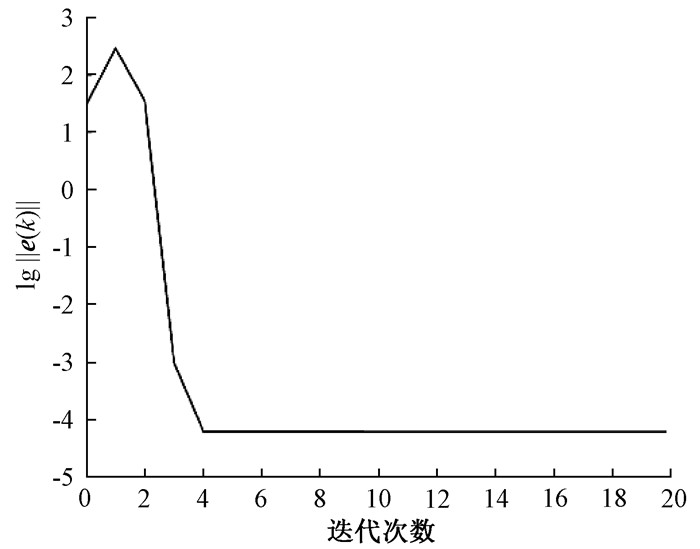
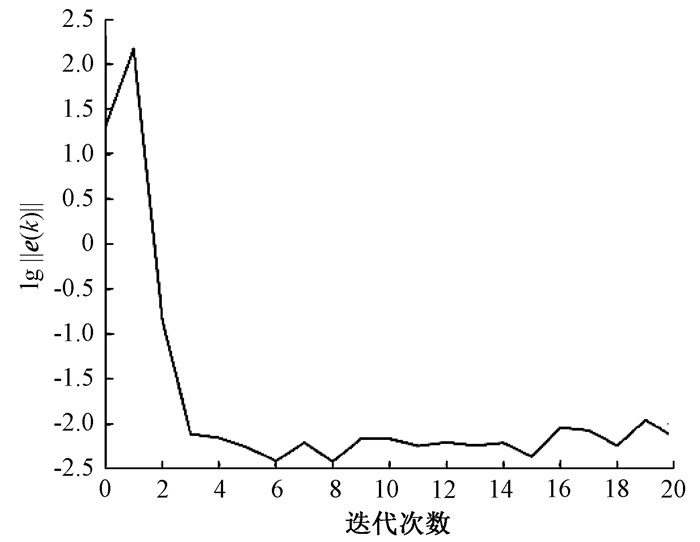
图 2给出了存在建模误差ΔG时,点到点二阶参数优化迭代学习控制算法的系统输出误差范数在迭代域上的收敛情况。图 3给出了存在非重复性外部干扰r时,点到点二阶参数优化迭代学习控制算法的系统输出误差范数在迭代域上的收敛情况。结合图 2和图 3可以得出,ΔG或r的存在使得算法(14)的跟踪性能受到了影响。但是随着迭代的进行,算法(14)仍然能够表现出良好的跟踪性能。
|
图 2 ΔG存在时,算法(14)的跟踪误差 Fig. 2 Tracking error of algorithm (14) when ΔG exists |
|
图 3 r存在时,算法(14)的跟踪误差 Fig. 3 Tracking error of algorithm (14) when r exists |
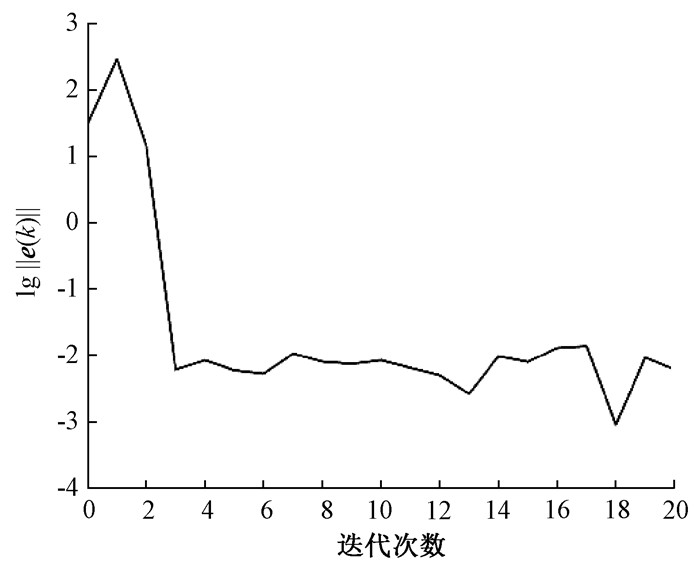
图 4给出了同时存在模型误差ΔG和非重复外部干扰r时,点到点二阶参数优化迭代学习控制算法的系统输出误差范数在迭代域上的收敛情况。结合前文分析和仿真结果,所提算法能够应对实际系统中存在的不确定性并表现出较好的跟踪性能。因此,可以将算法(14)应用到一类离散线性时不变系统的点到点跟踪控制问题中。
|
图 4 ΔG和r存在时,算法(14)的跟踪误差 Fig. 4 Tracking error of algorithm (14) when ΔG and r exist |
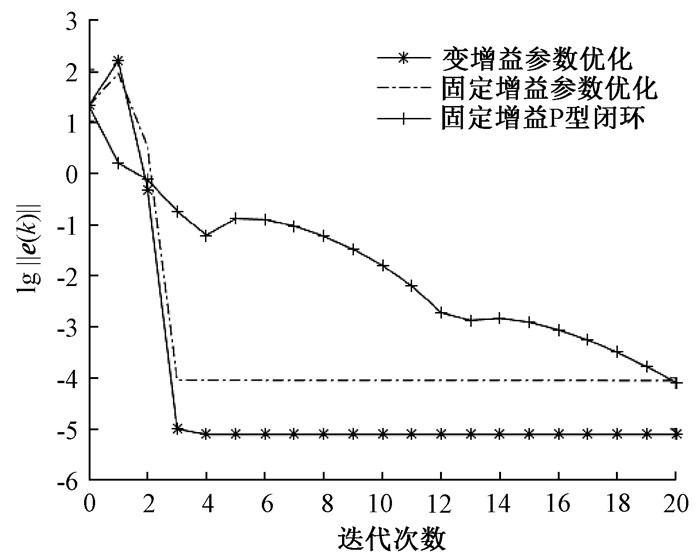
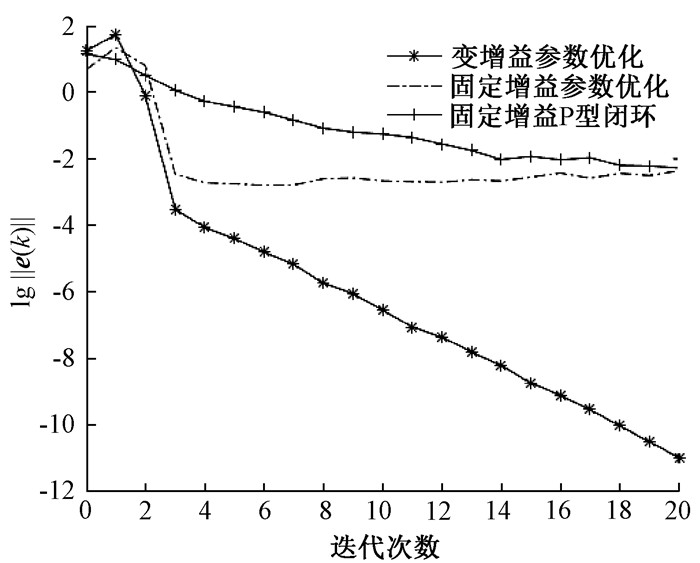
图 5给出了算法(14)、固定更新增益二阶参数优化算法、固定更新增益P型闭环[4]点到点迭代学习控制算法的系统输出误差范数,在迭代域上的收敛情况。图 6给出了存在模型误差ΔG和非重复外部干扰r时,3种算法更新后的参考轨迹,在非跟踪点处的输出与实际输出之间的误差范数在迭代域上的收敛情况。从图 6可以看出,采用算法(14)提高了参考轨迹的更新速率,快速逼近实际输出。
|
图 5 3种算法的跟踪性能比较 Fig. 5 Comparison of tracking performance among the three algorithms |
|
图 6 3种算法的轨迹更新速率比较 Fig. 6 Comparison of trajectory update rates among the three algorithms |
采用算法(14)的优势在于,一方面能够使参考轨迹快速更新;另一方面更多地利用以前多次迭代过程中已获得的信息来构造新的控制输入并对参数优化,提高了算法的收敛速度和跟踪精度。并且高阶算法能够削弱系统噪声对跟踪性能的影响,即使存在建模误差和输出误差等不确定性时,算法(14)仍然能够对系统(15)快速、高精度地跟踪控制。
4 结论针对一类离散线性时不变系统的点到点跟踪控制问题,本文提出一种快速参考轨迹更新的点到点二阶参数优化迭代学习控制算法。将参数优化思想和点到点迭代学习控制结合,用于点到点跟踪控制中,来提高算法的跟踪性能。在控制律的设计中采用时变的学习增益参数βk+1(t)来取代传统固定增益参数βk+1,使得参数的选取更加灵活自由,该算法同样适用于非正定系统。
与以往的研究成果相比,本文算法具有如下两个优点:第一,在进行参考轨迹更新过程中, 加入随迭代过程变化的指数变增益eγ(k),新的参考轨迹能够以更快的速度逼近系统输出;第二,考虑到高阶算法具备更好的跟踪性能,利用以前多次迭代过程的输入、输出信息来构造新的控制输入,并对参数进行优化,从而实现快速、高效的跟踪控制。
| [1] |
HOU Z S, WANG Y, YIN C K, et al. Terminal iterative learning control based station stop control of a train[J]. International journal of control, 2011, 84(7): 1263-1274. DOI:10.1080/00207179.2011.569030 (  0) 0) |
| [2] |
FREEMAN C T. Constrained point-to-point iterative learning control with experimental verification[J]. Control engineering practice, 2012, 20(5): 489-498. DOI:10.1016/j.conengprac.2012.01.003 (  0) 0) |
| [3] |
CHU B, FREEMAN C T, OWENS D H. A novel design framework for point-to-point ILC using suc-cessive projection[J]. IEEE transactions on control systems technology, 2015, 23(3): 1156-1163. DOI:10.1109/TCST.2014.2356931 (  0) 0) |
| [4] |
安通鉴, 刘祥官. 目标轨迹更新的点到点鲁棒迭代学习控制[J]. 浙江大学学报(工学版), 2015, 49(1): 87-92, 122. AN T J, LIU X G. Point-to-point robust iterative learning control via reference trajectory regulating[J]. Journal of Zhejiang university(engineering science), 2015, 49(1): 87-92, 122. (  0) 0) |
| [5] |
陶洪峰, 董晓齐, 杨慧中. 参考轨迹更新的点到点迭代学习控制算法优化及应用[J]. 控制理论与应用, 2016, 33(9): 1207-1213. TAO H F, DONG X Q, YANG H Z. Optimal algorithm and application for point to point iterative learning control via updating reference trajectory[J]. Control theory & applications, 2016, 33(9): 1207-1213. (  0) 0) |
| [6] |
董辉, 黄文嘉, 李林鑫. 变增益反馈D型迭代学习控制系统分析与仿真[J]. 浙江工业大学学报, 2014, 42(2): 214-218. DONG H, HUANG W J, LI L X. Analysis and simulation of iterative learning control system with switching gain D-type feedback[J]. Journal of Zhejiang university of technology, 2014, 42(2): 214-218. DOI:10.3969/j.issn.1006-4303.2014.02.019 (  0) 0) |
| [7] |
兰天一, 林辉. 区间可调节的变增益加速迭代学习控制[J]. 系统工程与电子技术, 2017, 39(4): 883-887. LAN T Y, LIN H. Accelerated iterative learning control algorithm with variable gain and adjustment of learning interval[J]. Systems engineering and electronics, 2017, 39(4): 883-887. (  0) 0) |
| [8] |
OWENS D H, FREEMAN C T, VAN DINH T. Norm-optimal iterative learning control with intermediate point weighting: theory, algorithms, and experimental evaluation[J]. IEEE transactions on control systems technology, 2013, 21(3): 999-1007. DOI:10.1109/TCST.2012.2196281 (  0) 0) |
| [9] |
OWENS D H, FREEMAN C T, CHU B. Generalized norm optimal iterative learning control with in-termediate point and sub-interval tracking[J]. International journal of automation and computing, 2015, 12(3): 243-253. DOI:10.1007/s11633-015-0888-8 (  0) 0) |
| [10] |
FREEMAN C T, TAN Y. Iterative learning control with mixed constraints for point-to-point tracking[J]. IEEE transactions on control systems technology, 2013, 21(3): 604-616. DOI:10.1109/TCST.2012.2187787 (  0) 0) |
| [11] |
JANSSENS P, PIPELEERS G, SWEVERS J. A data-driven constrained norm-optimal iterative learn-ing control framework for LTI systems[J]. IEEE transactions on control systems technology, 2013, 21(2): 546-551. DOI:10.1109/TCST.2012.2185699 (  0) 0) |
| [12] |
CHU B, FREEMAN C T, OWENS D H. A novel design framework for point-to-point ILC using suc-cessive projection[J]. IEEE transactions on control systems technology, 2015, 23(3): 1156-1163. DOI:10.1109/TCST.2014.2356931 (  0) 0) |
| [13] |
SON T D, AHN H S, MOORE K L. Iterative learning control in optimal tracking problems with specified data points[J]. Automatica, 2013, 49(5): 1465-1472. DOI:10.1016/j.automatica.2013.02.008 (  0) 0) |
| [14] |
逄勃, 邵诚. 高阶参数优化迭代学习控制算法[J]. 控制理论与应用, 2015, 32(4): 561-567. PANG B, SHAO C. High-order parameter-optimization iterative learning control algorithm[J]. Control theory & applications, 2015, 32(4): 561-567. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


