随着传统配电网逐步向主动配电网(active distribution network, ADN)[1]转变, 大量接入的光伏能源、风电和各种储能装置使得分布式电源(distributed generator, DG)的渗透率不断提高[2]。外界环境变化会影响风能和太阳能等可再生能源出力,从而使DG发电呈现间歇性,再加上负荷侧需求具有随机的特性,增加了电力系统的不确定性和可变性,导致在配电层面上系统的稳定性和经济性以及向终端用户供电的可靠性都面临巨大的挑战[3]。因此,考虑风光荷的不确定性,结合配电网主动管理措施实现有功-无功协调优化,在提高新能源消纳能力方面具有重要意义。
ADN动态优化模型属于最优潮流的范畴,本质上属于混合整数非线性规划(mixed integer non-linear programming, MINLP)[4]问题。目前,解决此种问题的方法主要有智能算法和数学规划两大类。文献[5]使用基于熵和距离的多目标粒子群算法,对DG接入配电网的优化选址进行分析。文献[6]针对传统粒子群算法种群多、样性少的缺陷,提出基于自学习迁移粒子群算法。但智能算法在计算过程中会反复调用潮流程序,导致求解时间较长,而且还会出现陷入局部最优解的问题。
近年来,以二阶锥规划(second-order cone programming, SOCP)为代表的凸规划技术被广泛应用于最优潮流和有功-无功协调优化等领域。文献[7]考虑了配电网中各种无功控制装置建立优化模型,并使用SOCP对模型中目标和约束条件进行凸处理,但对于风光荷的处理都是界定一个范围区间,并没有考虑风光荷的不确定性。本文考虑了风电和光伏的有功-无功输出特性,结合传统的无功优化措施实现配电网的有功-无功协调优化,以降低网损和提高DG的消纳能力,实现电网经济性运行; 结合风光荷的概率密度函数和比例选择法对风光荷的不确定性进行处理,运用快速前进法对场景进行削减,建立有多种主动管理措施参与的配电网有功-无功协调优化模型; 使用二阶锥松弛(second-order cone relaxation, SOCR)技术和大M法对原模型进行凸处理,进而转化为混合整数二阶锥规划(mixed integer second-order cone programming, MISOCP)问题,并采用IEEE 33节点配电网系统验证优化模型的有效性和精确性。
1 基于场景的随机模型 1.1 风光荷模型的建立 1.1.1 风电模型风电机组出力与当地风力资源紧密相连。目前,国内外研究结果表明,Weibull分布模型具有风速拟合度高、适应范围广的特点。因此,采用Weibull分布模型,风电机组出力与风速之间的关系可以表示为
| $ P_{\mathrm{W}}= \begin{cases}0, & 0 \leqslant v<v_{\mathrm{i}} \text { 或 } v_{\mathrm{o}} \leqslant v ,\\ P_{\mathrm{r}} \frac{v-v_{\mathrm{i}}}{v_{\mathrm{r}}-v_{\mathrm{i}}}, & v_{\mathrm{i}} \leqslant v<v_{\mathrm{r}}, \\ P, & v_{\mathrm{r}} \leqslant v<v_{\mathrm{o}},\end{cases} $ | (1) |
式中:Pr表示风力机组的额定输出功率; vi、vr、vo分别表示切入风速、额定风速、切出风速。
1.1.2 光伏模型光伏出力和光照强度的关系[8]可以表示为
| $ P_{\mathrm{PV}}= \begin{cases}P_{\mathrm{PV}_{\mathrm{r}}} \frac{I}{I_{\max }}, & I \leqslant I_{\max }, \\ P_{\mathrm{PV}_{\mathrm{r}}}, \quad & I>I_{\max },\end{cases} $ | (2) |
式中:PPVr为单个光伏的额定容量; I为当地实际光照强度; Imax为某时段内最大光照强度。
1.1.3 负荷模型负荷模型近似服从正态分布[8],可以表示为
| $ f\left(P_{\text {load }}\right)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π}}} \delta_{\mathrm{p}}}} \exp \left(-\frac{\left(P_{\text {load }}-\mu_{\mathrm{p}}\right)^{2}}{2 \delta_{\mathrm{p}}^{2}}\right), $ | (3) |
式中:Pload为负荷的有功功率; μp、δp2为负荷模型函数的期望和方差。
1.2 场景的建立与削减由于抽样、测量过程存在误差,与过去事件相关的数据可能会有一些不确定性,在预测过程中产生的误差会对数据预测带来影响。因此,含多种随机出力的DG和可变负荷的ADN也应在不确定框架下进行分析,使最终解的可靠性和精度接近现实中的最优解。本文在ADN优化分析中考虑电力负荷需求、风电和光伏出力的随机性,进行不确定性模型的建立。
1.2.1 场景的建立为了在建模时充分考虑不确定性,将与电力负荷需求、风电和光伏出力相关的预测误差视为具有已知概率密度函数(probability density function, PDF)的随机变量,使用比例选择法来产生场景。情景s的电力负荷需求、风电和光伏出力可以表示为
| $ P_{\mathrm{L}, t, s}=P_{\mathrm{L}, t, s}^{\mathrm{forecasted}}+\Delta P_{\mathrm{L}, t, s}, t=1,2, \cdots, 24, s=1,2, \cdots, N_{s}, $ | (4) |
| $ P_{\mathrm{DG}, t, s}=P_{\mathrm{DG}, t, s}^{\mathrm{forecasted}}+\Delta P_{\mathrm{DG}, t, s}, t=1,2, \cdots, 24, s=1,2, \cdots, N_{s}, $ | (5) |
式中:PL, t, sforecasted、PDG, t, sforecasted是现有的负荷预测数据; ΔPDG, t, s和ΔPL, t, s分别是t时刻DG输出有功功率和负荷有功功率预测值的误差,DG中包含风电和光伏出力。
为了针对负荷和DG出力的随机性生成情景,必须将每个随机变量的PDF离散化,目的是将具有连续特性的概率误差函数转变为对应的离散概率误差函数,以方便对各时段的预测误差进行计算。
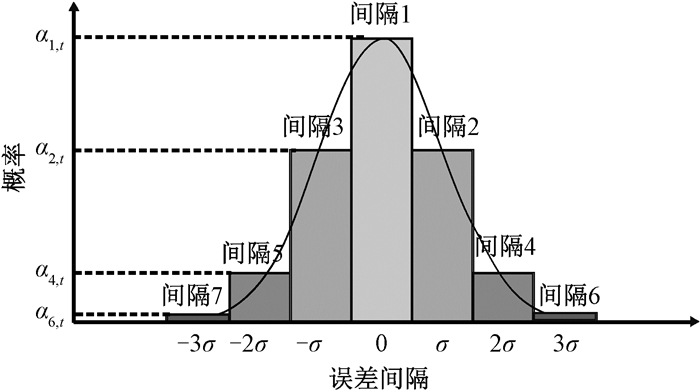
选取负荷需求、光伏、风电的PDF为正态分布随机函数,如图 1所示,考虑了7个以零均值为中心的间隔,每个间隔的宽度等于标准预测误差σ,偏差等于预测值的10%,每个间隔在时间t的概率用αi, t表示。
|
图 1 负荷需求、光伏、风电的PDF Fig. 1 PDF of load demand, photovoltaic and wind power |
为了用一个特定的随机变量来对每个概率水平建模,使用比例选择法[9]。首先产生一个区间为[0, 1]的随机数,然后根据随机数的值,让它落在[0, 1]内代表不同概率值的7个子区间(间隔1~7)中。[0, 1]区间概率累计如图 2所示,子区间对应的概率值为在该随机数选择下预测误差的概率。

|
图 2 [0, 1]区间概率累计 Fig. 2 [0, 1] interval cumulative probability |
引入二进制参数B(i, t, s)uncertainty,该变量与随机选择的负荷、风电和光伏预测误差相关。若产生的随机数落在子区间[a, b],则与此子区间有关的二进制参数B(i, t, s)uncertainty为1,此时选择该区间对应的误差值作为预测误差。
各场景描述可以表示为
| $ {scenario}(s)=\left[B_{(1, t, s)}^{\mathrm{L}}, \cdots, B_{(7, t, s)}^{\mathrm{L}}, B_{(1, t, s)}^{\mathrm{W}}, \cdots, B_{(7, t, s)}^{\mathrm{W}}, B_{(1, t, s)}^{\mathrm{PV}}, \cdots, B_{(7, t, s)}^{\mathrm{PV}}\right]_{t=1,2, \cdots, 24}。$ | (6) |
各场景所对应的概率可以表示为
| $ \pi_{s}=\frac{\prod\limits_{t=1}^{24}\left(\sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{L}} \times \alpha_{i, t}\right) \times \sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{W}} \times \beta_{i, t}\right) \times \sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{PV}} \times \gamma_{i, t}\right)\right)}{\sum\limits_{s=1}^{N_{s}}\left(\prod\limits_{t=1}^{24}\left(\sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{L}} \times \alpha_{i, t}\right) \times \sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{W}} \times \beta_{i, t}\right) \times \sum\limits_{i=1}^{7}\left(B_{(i, t, s)}^{\mathrm{PV}} \times \gamma_{i, t}\right)\right)\right)}, $ | (7) |
式中:B(i, t, s)L、B(i, t, s)W、B(i, t, s)PV分别为用于电力负荷、风力和光伏发电的情景s中t时刻的二进制参数; αi, t、βi, t、γi, t为t时刻电力负荷、风力和光伏发电预测误差对应的概率。
1.2.2 场景削减在场景生成过程之后,可能会出现某些场景是相同的,出现概率低的场景应从场景集中删除,这个过程称为场景削减。所涉及的随机过程的场景数量越多,越能精确地模拟所考虑的风光荷不确定性。然而,大量的场景会使计算过程变得复杂,降低求解速度。
本文采用快速前进法进行场景削减,主要根据各个场景出现的概率计算场景间的相对距离,削减场景中孤立的样本,具体步骤详见文献[10]。
2 有功-无功协调优化模型 2.1 目标函数的建立为了提高电网运行的经济性,同时增大配电系统对新能源的消纳能力,以电网运行成本为目标函数,其包含以下3个部分:购电成本Wgrid; 网络损耗成本Wloss; 燃气轮机二次成本WGT。
目标函数表达式为
| $ \left\{\begin{array}{l} W=W_{\text {grid }}+W_{\text {loss }}+W_{\mathrm{GT}}, \\ W_{\text {grid }}=C_{1} \sum\limits_{t=1}^{24} P_{\text {grid }, t}, \\ W_{\text {loss }}=C_{2}\left|\sum\limits_{i, j \in E} \sum\limits_{t=1}^{24} r_{i j} \frac{P_{i j, t}^{2}+Q_{i j, t}^{2}}{U_{i, t}^{2}}\right|, \\ W_{\mathrm{GT}}=\sum\limits_{t=1}^{24} \sum\limits_{i \in Y}\left(a_{i} P_{i, t}^{2}+b_{i} P_{i, t}+c_{i}\right), \end{array}\right. $ | (8) |
式中:Pgrid为上级电网提供的有功功率; E为有联络关系的支路集合; Pij, t、Qij, t为t时刻节点i流向节点j的有功、无功功率; Ui, t为t时刻节点i的电压幅值; C1为购电系数,本文基于峰谷平电价机制,峰时段09:00—15:00、19:00—21:00为1元/(kW·h),平时段15:00—19:00、21:00—23:00为0.8元/(kW·h),谷时段23:00—09:00为0.5元/(kW·h); C2为网损费用系数,取0.8元/(kW·h)[11]; WGT考虑发电成本一致性[12],使用二次函数表示,ai、bi、ci为发电成本的系数,分别为0.18、418、150;Pi, t为t时刻第i台燃气轮机的有功出力; Y为燃气轮机接入节点的集合。
2.2 约束条件使用有递归特性的Distflow潮流模型,以支路功率为基础建立潮流方程
| $ \left\{\begin{array}{l} \sum\limits_{i \in v(j)}\left(P_{i j, t}-r_{i j} \frac{P_{i j, t}^{2}+Q_{i j, t}^{2}}{U_{i, t}^{2}}\right)=\sum\limits_{k \in w(j)} P_{j k, t}+P_{j, t}, \\ \sum\limits_{i \in v(j)}\left(P_{i j, t}-x_{i j} \frac{P_{i j, t}^{2}+Q_{i j, t}^{2}}{U_{i, t}^{2}}\right)=\sum\limits_{k \in w(j)} Q_{j k, t}+Q_{j, t}, \\ P_{j, t}=P_{j, t}^{\mathrm{GT}}+P_{j, t}^{\operatorname{wind}}+P_{j, t}^{\mathrm{pv}}+P_{j, t}^{\mathrm{dis}}-P_{j, t}^{\mathrm{ch}}-P_{j, t}^{\mathrm{load}}, \\ Q_{j, t}=Q_{j, t}^{\text {wind }}+Q_{j, t}^{\mathrm{pv}}+Q_{j, t}^{\mathrm{SVG}}-Q_{j, t}^{\mathrm{load}}, \end{array}\right. $ | (9) |
| $ U_{j, t}^{2}=U_{i, t}^{2}-2\left(r_{i j} P_{i j, t}+x_{i j} Q_{i j, t}\right)+\left(r_{i j}^{2}+x_{i j}^{2}\right) \frac{P_{i j}^{2}+Q_{i j}^{2}}{U_{i}^{2}}, \quad \forall(i, j) \mid i, j \in E, $ | (10) |
| $ \left(U_{i, t} I_{i j, t}\right)^{2}=P_{i j, t}^{2}+Q_{i j, t}^{2}, \quad \forall(i, j) \mid i, j \in E, $ | (11) |
式中:Pj, tGT是t时刻j节点由上级电网注入的有功功率; Pj, twind、Qj, twind是t时刻j节点注入的风力有功、无功功率; Pj, tpv、Qj, tpv是t时刻j节点注入的光伏有功、无功功率; Pj, tload、Qj, tload是t时刻j节点处的有功、无功负荷; v(j)是以j节点为子节点的支路首端节点集合; w(j)是以j节点为父节点的支路末端节点集合; Pj, tch、Pj, tdis是j节点储能装置t时刻充电、放电功率; Qj, tSVG是t时刻j节点连续无功补偿装置对电网的输送功率。规定:功率正方向由i到j,节点注入的功率为正,节点流出的功率为负。
2.2.1 电网安全运行边界条件约束配电网要安全可靠的运行,必须保证任意时刻满足各电力设备的边界条件。根据本文所建模型,节点电压幅值的标幺值、各支路电流、静止无功补偿装置无功出力、燃气轮机有功和无功出力以及可再生DG有功和无功出力均要在设定的上下限区间内。
2.2.2 有载调压变压器(OLTC)模型约束考虑到变压器的分接头频繁操作会降低其使用寿命,以及为保障变压器设备的正常运行,在OLTC模型中限制分接头每日操作次数。
OLTC任意一个分接头挡位可以表示为
| $ \left\{\begin{array}{l} k_{i j}^{2}=k_{i j, \min }^{2}+\sum\limits_{k_{t}=1}^{N_{\mathrm{T}}^{-1}}\left(k_{t}^{2} \Delta \tau^{2}+2 k_{t}^{2} \Delta \tau k_{i j, \min }\right) \xi_{i j, k_{t}}, \\ \sum\limits_{k_{t}=1}^{N_{\mathrm{T}}-1} \xi_{i j, k_{t}} \leqslant 1, \xi_{i j, k_{t}} \in\{0,1\}, \quad \forall(i, j) \in A, \end{array}\right. $ | (12) |
| $ \sum\limits_{t=1}^{23} \sum\limits_{k_{t}=1}^{N_{\mathrm{T}}}\left|\xi_{i j, k_{t}}-\xi_{i j, k_{t+1}}\right| \leqslant 2 N_{\max }, $ | (13) |
式中:Δτ为OLTC变比的调节步长; NT为分接头挡位数; A为变压器所在支路的集合; ξij, kt表示t时刻分接头挡位kt的使用状态,1代表t时刻使用该分接头,0代表t时刻没有使用该分接头; kij, min代表i-j支路OLTC的最小变比; Nmax代表OLTC分接头每日允许的最大调节次数。
2.2.3 电池储能装置(ESS)约束ESS在电网运行时需要考虑到充放电在同一时刻只能存在一个状态,包括储能装置的总容量、充放电的功率以及日充放电次数允许值。因此,对ESS的约束处理可以表示为
| $ \mu_{i, t}^{\mathrm{ch}}+\mu_{i, t}^{\mathrm{dis}}=1, $ | (14) |
| $ \left\{\begin{array}{l} 0 \leqslant P_{i, t}^{\mathrm{dis}} \leqslant \mu_{i, t}^{\mathrm{dis} } P_{\mathrm{ESS}}^{\mathrm{dis}, \max }, \\ 0 \leqslant P_{i, t}^{\mathrm{ch}} \leqslant \mu_{i, t}^{\mathrm{ch}} P_{\mathrm{ESS}}^{\mathrm{ch}, \max }, \end{array}\right. $ | (15) |
| $ E_{i, t+1}^{\mathrm{ESS}}=E_{i, t}^{\mathrm{ESS}}(1-\eta)+\eta^{\mathrm{ch}} P_{i, t}^{\mathrm{ch}} \Delta T-\frac{1}{\eta^{\mathrm{dis}}} P_{i, t}^{\mathrm{dis}} \Delta T, $ | (16) |
| $ \left\{\begin{array}{l} \sum\limits_{t=1}^{24}\left|\mu_{i, t+1}^{\mathrm{ch}}-\mu_{i, t}^{\mathrm{ch}}\right| \leqslant \lambda_{\max }^{\mathrm{ESS}}, \\ \sum\limits_{t=1}^{24}\left|\mu_{i, t+1}^{\mathrm{dis}}-\mu_{i, t}^{\mathrm{dis}}\right| \leqslant \lambda_{\max }^{\mathrm{ESS}}, \end{array}\right. $ | (17) |
式中:μi, tch、μi, tdis表示t时刻i节点的ESS的充电、放电状态; Ei, tESS为节点i的ESS在t时刻的储电容量; PESSch,max、PESSdis,max表示ESS最大充电、放电功率; η为自放电率; ηch和ηdis为ESS的充电、放电效率; λmaxESS为ESS一天内充放电最大次数,本文设定日最大充放电次数为4。
2.3 模型的分析与简化 2.3.1 基于SOCP的模型简化SOCP约束条件与目标函数均与设置的决策变量呈线性关系,而决策变量可由锥内部数值得到,因此也叫作线性锥规划[13]。引入变量Isqij, t=Iij, t2,Ui, tsq=Ui, t2,消除原模型中约束和目标函数中的二次项,将原问题转化为SOCP问题。
引入的变量Isqij, t、Usqi, t可以根据潮流方程的等价表达式(11),引入旋转二阶锥的约束转化:(Ui, tIij, t)2≤Pij, t2+Qij, t2,通过二阶锥松弛转化为
| $ \left\| \begin{gathered} 2 P_{i j, t} \\ 2 Q_{i j, t} \\ I_{i j, t}^{s q}-U_{i, t}^{s q} \end{gathered}\right\|_2\leqslant I_{i j, t}^{s q} U_{i, t}^{s q}。$ | (18) |
当线性规划问题的约束条件存在等于或大于运算形式时,可以使用大M法进行简化处理。通过引入若干0-1二值变量,将原非线性约束等价地转化为混合整数线性约束[14],大M法的应用主要体现在OLTC模型的转化。
对式(12)进行线性化处理,可得
| $ \left\{\begin{array}{l} k_{i j}^{2} U_{j, t}^{s q}=k_{i j, \min }^{2} U_{j, t}^{s q}+\sum\limits_{k_{t}=1}^{N_{\mathrm{T}}-1} y_{j, k_{t}}\left(k_{t}^{2} \Delta \tau^{2}+2 k_{t}^{2} \Delta \tau k_{i j, \min }\right) ,\\ -M\left(1-\xi_{i j, k_{t}}\right)+U_{j, t}^{s q} \leqslant y_{j, k_{t}} \leqslant M\left(1-\xi_{i j, k_{t}}\right)+U_{j, t}^{s q}, \\ -M \xi_{i j, k_{t}} \leqslant y_{j, k_{t}} \leqslant M \xi_{i j, k_{t}}, \xi_{i j, k_{t}} \in\{0,1\}, \\ \sum\limits_{k_{t}=1}^{N_{\mathrm{T}}-1} \xi_{i j, k_{t}} \leqslant 1。\end{array}\right. $ | (19) |
针对建立的配电网优化模型,在Matlab-Yalmip平台下进行编程,使用Gurobi优化器求解。采用IEEE 33节点配电网系统对所建立的模型进行有效性验证。基准电压为12.66 kV,选取系统基准容量为10 MVA,电压基准标幺值为1.0,设定节点1为平衡节点,考虑到配电网辐射式运行条件,系统节点电压标幺值上限和下限分别为1.05、0.95。其中,OLTC设定位于节点1和节点18,变比可调区间为[0.95, 1.05],调节步长为0.01,共计11个挡位,日最大动作次数为4。SVG安装节点为3、18,调节区间分别为[-0.2, 2]、[-0.1, 1]。系统中接入的风电位于节点5和节点9,额定容量为3 MW; 系统中接入的光伏位于节点6和节点16,额定容量为1 MW。ESS位于节点6(ESS-6)和节点13(ESS-13),其中充电、放电效率分别为0.98和0.85,最大充电、放电功率分别为0.5 MW和0.3 MW,初始电量为0.3 MW·h,最大电量为2 MW·h。燃气轮机(GT)位于节点7(GT-7)和节点27(GT-27),最大有功出力分别为3 MW和0.75 MW,最大无功出力均为1.5 MW。风速、光照强度数据来自数值天气预报(numerical weather prediction,NWP),风电、光伏和负荷的预测误差取为预测值的10%。根据场景法生成1 000个样本数据,利用削减技术将场景削减为10个,选取最大概率的场景作为基础数据输入。
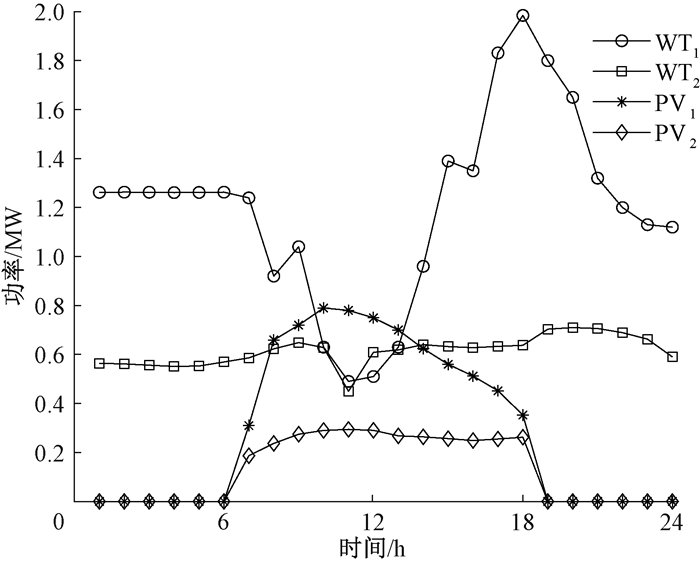
3.2 DG出力情况及系统储能装置优化分析风电、光伏有功出力曲线如图 3所示。可以看出,风电在夜间出力最大,白天出力相对较小,符合风力变化的客观事实; WT1、WT2接入节点5和节点9,节点5为节点9的前端节点,所带负荷更多,因此WT1出力更大; WT1、WT2的有功出力均在3 MW以内。光伏发电在6时至18时有功率输出,在12时输出有功功率达到最大,输出功率在1 MW以内。
|
图 3 风电、光伏有功出力曲线 Fig. 3 Wind power and photovoltaic active power output curve |
储能装置在配电系统中合理的充放电过程可以充分消纳DG过剩出力,改善系统存在的弃风、弃光情况,从而增大系统对风电及光伏出力的消纳水平,减小电网运行总成本。储能系统接入前后,系统对风电及光伏出力的消纳量增加0.57 MW,可以看出,储能装置的接入对过剩的风电及光伏出力起到一定的消纳作用。同时,增加储能装置前后,目标总成本由41 839元缩减到40 617元,节省成本1 222元。
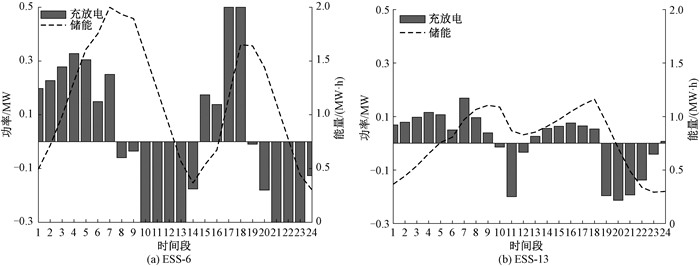
3.3 ESS充放电情况及其荷电状态分析ESS分别接入节点6和节点13,图 4为ESS充放电功率与荷电状态的变化曲线。图中的功率纵轴为ESS充放电状态参考轴,能量纵轴为ESS荷电状态参考轴,柱状图表示充放电过程功率的变化情况。对于ESS-6而言,在[0, 7]、[15, 18]时间段充电,在[8, 14]、[19, 23]时间段放电,日充放电次数为4;对于ESS-13而言,在[0, 9]、[13, 18]时间段充电,在[10, 12]、[19, 23]时间段放电,日充放电次数为4。可以看出,两个储能装置的日充放电次数均满足约束。
|
图 4 ESS充放电功率与荷电状态曲线 Fig. 4 ESS charge and discharge power and state-of-charge curve |
以ESS-6为例,结合图 3的风电、光伏有功出力曲线进行充放电过程分析。ESS-6在光伏出力为0且风电出力较大的[0, 7]、[15, 18]时间段处于充电状态,结合峰谷平电价机制可以得出,充电过程对应着购电价格较低且DG输出较大的时间段,增加了电能消纳能力,在购电谷时储存电能。而放电过程为居民用电高峰期[8, 14]、[19, 23]时间段,该区间对应着购电峰时电价,将在购电谷时储存的电能在购电峰时投入电网,降低了电网的购电成本。
ESS-6、ESS-13的电量在24时为0.3 MW·h,满足在一个优化周期内变化量为0。以ESS-6为例,对储能装置中电量与充放电状态进行对应分析,可以看出,储能装置电量增加的时间段对应着充电过程,[0, 7]时间段风电出力较大时储能装置开始充电,将电量转化为荷电状态,直到7时达到最大,[8, 14]时间段对应储能装置放电状态,此时储存的电量被释放,曲线呈下降趋势。
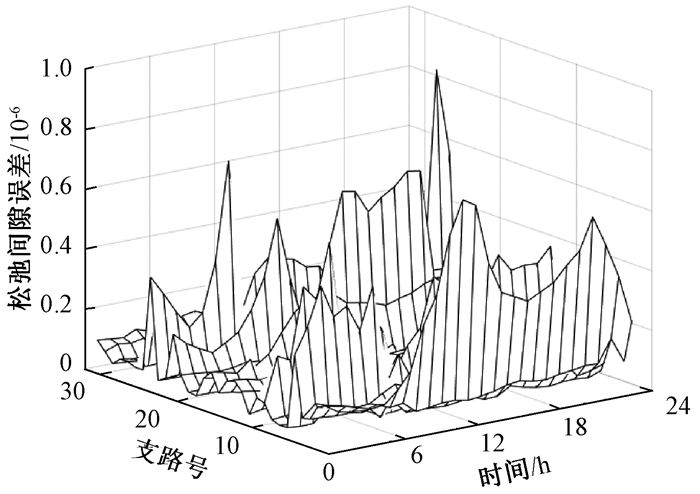
3.4 松弛误差精度分析SOCR的核心思想是将非凸等式松弛为旋转二阶锥的不等式约束,然后运用现阶段成熟的商业软件进行求解。式(18)进行二阶锥松弛后,降低了约束条件求解难度,同时扩大了最优解求解范围,可能会对重构目标最优解对应的决策变量值产生影响,使用error=(Pij, t2+Qij, t2)-Ui, tsqIsqij, t来检验二阶锥松弛精度。图 5为松弛间隙误差图,可以看出,每条支路的二阶锥松弛偏差数量级均小于10-6,满足精度要求。
|
图 5 松弛间隙误差图 Fig. 5 Slack gap error graph |
为了实现对高比例新能源接入的配电网进行协调优化,提高配电网运行的经济性,本文同时考虑风光储接入下配电系统的有功-无功优化问题。首先,针对风光荷的不确定性使用比例选择法进行场景生成,再基于快速前进法进行场景削减; 其次,建立风光储以及多种主动管理措施模型,基于二阶锥松弛技术和大M法对优化模型中混合整数非线性约束进行凸处理,建立了MISOCP模型; 最后,通过对所建立模型的算例分析,验证了协调优化思想的有效性。
| [1] |
陈旭, 张勇军, 黄向敏. 主动配电网背景下无功电压控制方法综述[J]. 电力系统自动化, 2016, 40(1): 143-151. CHEN X, ZHANG Y J, HUANG X M. Review of reactive power and voltage control method in the background of active distribution network[J]. Automation of electric power systems, 2016, 40(1): 143-151. (  0) 0) |
| [2] |
刘东, 陈云辉, 黄玉辉, 等. 主动配电网的分层能量管理与协调控制[J]. 中国电机工程学报, 2014, 34(31): 5500-5506. LIU D, CHEN Y H, HUANG Y H, et al. Hierarchical energy management and coordination control of active distribution network[J]. Proceedings of the CSEE, 2014, 34(31): 5500-5506. (  0) 0) |
| [3] |
吴克河, 王继业, 李为, 等. 面向能源互联网的新一代电力系统运行模式研究[J]. 中国电机工程学报, 2019, 39(4): 966-979. WU K H, WANG J Y, LI W, et al. Research on the operation mode of new generation electric power system for the future energy Internet[J]. Proceedings of the CSEE, 2019, 39(4): 966-979. (  0) 0) |
| [4] |
郑能, 丁晓群, 郑程拓, 等. 含高比例光伏的配电网有功-无功功率多目标协调优化[J]. 电力系统自动化, 2018, 42(6): 33-39, 91. ZHENG N, DING X Q, ZHENG C T, et al. Multi-objective coordinated optimization of active and reactive power for distribution network integrated with high proportion of photovoltaic generation[J]. Automation of electric power systems, 2018, 42(6): 33-39, 91. (  0) 0) |
| [5] |
栗然, 马慧卓, 祝晋尧, 等. 分布式电源接入配电网多目标优化规划[J]. 电力自动化设备, 2014, 34(1): 6-13. LI R, MA H Z, ZHU J Y, et al. Multi-objective optimization for DG integration into distribution system[J]. Electric power automation equipment, 2014, 34(1): 6-13. DOI:10.3969/j.issn.1006-6047.2014.01.002 (  0) 0) |
| [6] |
邓长虹, 马庆, 肖永, 等. 基于自学习迁移粒子群算法及高斯罚函数的无功优化方法[J]. 电网技术, 2014, 38(12): 3341-3346. DENG C H, MA Q, XIAO Y, et al. Reactive power optimization based on self-learning migration particle swarm optimization and Gaussian penalty function[J]. Power system technology, 2014, 38(12): 3341-3346. (  0) 0) |
| [7] |
陆海强, 缪辉. 考虑多种主动管理措施的配电网有功-无功协调优化[J]. 电工技术, 2020(5): 84-89. LU H Q, MIAO H. Active-reactive power coordinated optimization of distribution network considering multiple active management strategies[J]. Electric engineering, 2020(5): 84-89. (  0) 0) |
| [8] |
张沈习, 李珂, 程浩忠, 等. 考虑相关性的间歇性分布式电源选址定容规划[J]. 电力系统自动化, 2015, 39(8): 53-58, 140. ZHANG S X, LI K, CHENG H Z, et al. Optimal siting and sizing of intermittent distributed generator considering correlations[J]. Automation of electric power systems, 2015, 39(8): 53-58, 140. (  0) 0) |
| [9] |
MOHAMMADI S, SOLEYMANI S, MOZAFARI B. Scenario-based stochastic operation management of MicroGrid including wind, photovoltaic, micro-turbine, fuel cell and energy storage devices[J]. International journal of electrical power & energy systems, 2014, 54: 525-535. (  0) 0) |
| [10] |
郑能, 丁晓群, 管志成, 等. 基于场景法的配电网有功-无功协调优化[J]. 电网技术, 2019, 43(5): 1640-1651. ZHENG N, DING X Q, GUAN Z C, et al. Coordinated optimization of active power and reactive power in distribution network based on scenario method[J]. Power system technology, 2019, 43(5): 1640-1651. (  0) 0) |
| [11] |
PINEDA S, CONEJO A J. Scenario reduction for risk-averse electricity trading[J]. IET generation, transmission & distribution, 2010, 4(6): 694-705. (  0) 0) |
| [12] |
席磊, 李玉丹, 黄悦华, 等. 基于虚拟狼群控制策略的智能发电控制[J]. 中国电机工程学报, 2018, 38(10): 2966-2979, 3147. XI L, LI Y D, HUANG Y H, et al. Smart generation control based on the virtual wolf pack control strategy[J]. Proceedings of the CSEE, 2018, 38(10): 2966-2979, 3147. (  0) 0) |
| [13] |
凌武能, 杭乃善, 兰飞. 求解最优潮流问题的混合线性锥规划法[J]. 中国电机工程学报, 2016, 36(10): 2638-2647. LING W N, HANG N S, LAN F. Solution of optimal power flow problems by mixed cone linear programming[J]. Proceedings of the CSEE, 2016, 36(10): 2638-2647. (  0) 0) |
| [14] |
TAYLOR J A, HOVER F S. Convex models of distribution system reconfiguration[J]. IEEE transactions on power systems, 2012, 27(3): 1407-1413. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


