配电网中性点主要的接地方式有中性点不接地系统和中性点经消弧线圈接地系统.中性点经消弧线圈接地系统由于消弧线圈的电感抵消了全系统线路的对地电容,若消弧线圈的参数配置合适,当系统中出现单相接地短路故障时,不会使非故障相对地电压升高数值过大,可以有效地抑制弧光接地过电压,减少甚至消除流经接地点的故障电流.
中性点经消弧线圈接地系统的特征可以概括为:1)有效地减少单相接地故障的故障电流,避免系统出现的弧光接地过电压对电网设备绝缘造成破坏;2)可以使电网出现接地故障时继续带负载运行数小时,给线路检修人员足够的时间去查明故障点和消除故障,而不影响供电;3)由于消弧线圈的过补偿作用,降低了线路故障时的谐振过电压概率,降低了过电压倍数.实践证明,采用了自动调谐消弧线圈后,配电网年平均故障跳闸次数大幅减少.
电网中用于接地系统的消弧线圈主要有分级可调调匝式消弧线圈和直流偏磁式磁控消弧线圈[1-3].目前已有大量的文献对中性点经消弧线圈接地系统进行研究,这些研究主要集中在消弧线圈接地系统的稳态特性分析[4]、暂态特性分析[5-7]以及接地选线判别方面[8-12],这些分析都是基于电网的分布参数为固定值和消弧线圈是一个固定电抗值来分析的,并未考虑接地故障引起电网参数的改变以及消弧线圈的调节过程,这样得出的结果与实际不符,在工程实践中难以得到应用.针对这种情况,本文给出一种考虑消弧线圈调节过程的配电网线路接地故障时暂、稳态分析方法,以满足工程实际的需要.
1 调匝式可控消弧线圈数学模型目前供电部门使用的消弧线圈大部分为调匝式消弧线圈,其由两部分构成:有载调压开关和具备多个调节档位的消弧线圈.消弧线圈的工作特性接近于线性.通过有载调压开关可以接近线性地改变其自身电感.调匝式消弧线圈的工作特性可以用其工作电流iL、两端电压uL、工作档位N及线圈电感L等几个主要参数来描述.调匝式可控消弧线圈的数学模型可用其两端电压uL与线圈电流iL之间的关系来描述,uL=kLdiL/dt+kRL,其中:L、RL为整个消弧线圈的电感和电阻;k为当前工作档位对应电感与线圈总电感的比值.
电流调节范围在I1~IN之间按等差电流调节分接头,其比例系数k=I1/L(I1+Nnow(IN-I1/N)),非等差电流调节分接头的比例系数k可根据当前档位实际电流通过查表方式来获得.
设调匝式消弧线圈开始调匝时刻为T,调匝时间为ΔT,则调匝前后工作电流为
| $ {i_L} = \left\{ {\begin{array}{*{20}{l}} {{i_E} - {i_{C\mathit{\Sigma }}},}&{t \le T + \Delta T}\\ { - \left( {1 + g} \right){i_{C\mathit{\Sigma },}}}&{t > T + \Delta } \end{array},} \right. $ |
其中:iE为流过接地点的故障电流;iCΣ为线路对地总电容电流;g(0<g<1)为由于消弧线圈档位不连续,且为了避免过渡过程中出现谐振,采用过补偿方式引入的过补偿系数.
2 中性点经调匝式消弧线圈接地系统的稳态特性分析不失一般性,考虑系统发生单相接地时的接地电阻的影响,中性点经消弧线圈接地后,消弧线圈将提供一个感性电流,用于补偿系统对地分布电容的容性电流,从而减少发生接地故障后流经故障接地点的故障电流,减少接地燃弧电流及弧光过电压.
根据消弧线圈对电容电流补偿程度的不同,消弧线圈有全补偿(IL=ICΣ)、欠补偿(IL<ICΣ)和过补偿(IL>ICΣ)3种方式.过补偿方式补偿后残余电流为感性,可以避免串联谐振引起的过电压,在实际工程中得到了广泛的应用.
中性点经调匝式消弧线圈接地系统发生单相接地故障后,接地电流分布如图 1所示.
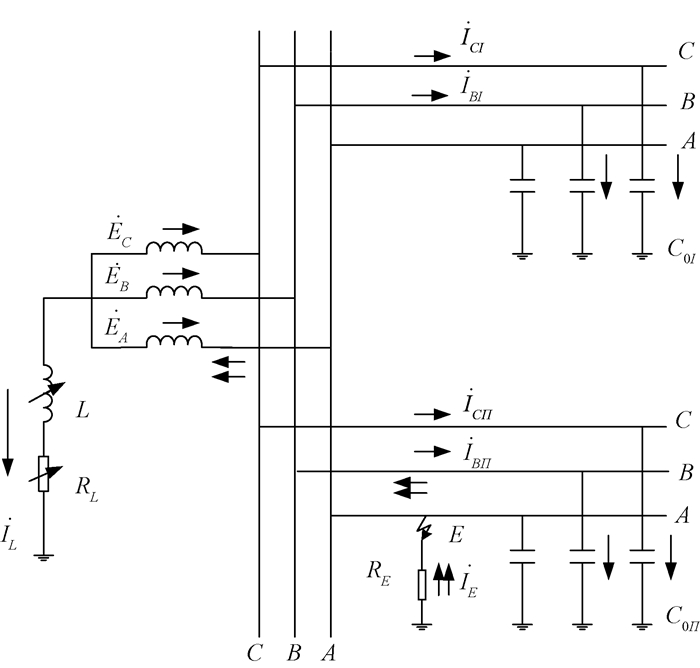
|
图 1 中性点经消弧线圈接地系统单相接地电流分布 Figure 1 Single phase grounding current distribution of neutral point via arc suppression coil grounding system |
下面针对调匝式消弧线圈的调节过程中的各个阶段(以A相接地为例)进行稳态分析.
a) 系统发生接地故障前, 消弧线圈中流经的电流为系统的不平衡零序电流ΔI0,其两端电压为中性点对地零序电压ΔU0,在实际工程中认为这两项都很小,可以忽略不计.
b) 系统发生接地故障时消弧线圈调档前, 此时消弧线圈两端电压接近于系统相电压,设故障点接地电阻为RE,则有
| $ {{\dot I}_L} = \frac{{{{\dot E}_A}}}{{{\rm{j}}\omega \left( {L - 3\omega {C_{0\mathit{\Sigma }}}{R_L}} \right) + \left( {{R_L} - {R_E} + {\omega ^2}L3\omega {C_{0\mathit{\Sigma }}}{R_E}} \right)}};{{\dot I}_E}\frac{{{{\dot E}_A}\left( {1 + {\rm{j}}3\omega {C_{0\mathit{\Sigma }}}{R_L} - 3{\omega ^2}l{C_{0\mathit{\Sigma }}}} \right)}}{{\left( {{R_L} - {R_E} + {\omega ^2}L3\omega {C_{0\mathit{\Sigma }}}{R_E}} \right) + {\rm{j}}\omega \left( {L - 3{C_{0\mathit{\Sigma }}}{R_L}} \right)}}. $ |
以上即为不考虑消弧线圈调节作用时的稳态特性分析方程及分析结果.
c) 系统发生接地故障时消弧线圈调档后, 此时消弧线圈流过补偿的电感电流为
| $ {{\dot I'}_E} = \frac{{{{\dot E}_A}\left( {2 + g} \right){\rm{j}}3\omega {C_{0\mathit{\Sigma }}}\left( {{R_L} + {\rm{j}}\omega L} \right)}}{{\left( {{R_L} - {R_E} + {\omega ^2}L3\omega {C_{0\mathit{\Sigma }}}{R_E}} \right) + {\rm{j}}\omega \left( {L - 3{C_{0\mathit{\Sigma }}}{R_L}} \right)}};{{\dot I'}_L} = \frac{{{{\dot E}_A}\left( {1 + g} \right){\rm{j}}3\omega {C_{0\mathit{\Sigma }}}\left( {{R_L} + {\rm{j}}\omega L} \right)}}{{\left( {{R_L} - {R_E} + {\omega ^2}L3\omega {C_{0\mathit{\Sigma }}}{R_E}} \right) + {\rm{j}}\omega \left( {L - 3{C_{0\mathit{\Sigma }}}{R_L}} \right)}}. $ |
通过上面的分析可以得出以下结论:
1) 中性点经消弧线圈接地系统发生单相接地故障时,系统参数会发生改变,该变化会引起消弧线圈调匝动作.
2) 接地后消弧线圈调匝前流过的电流为系统对地电容电流与流经故障点的电流的差值,调匝后流过的电流为系统对地电容电流的(1+g)倍.
3) 考虑接地电阻的影响后,流过故障点的电流不再与故障相电压存在90°相角关系,故障相零序电流不超前于零序电压90°.
3 调匝式消弧线圈接地系统的暂态特性分析中性点经消弧线圈接地系统发生单相接地时,线路故障电流包括线路对地电容电流和流过消弧线圈的电感电流.线路的对地电容电流的暂态分量虽然持续时间较短,但其分量值往往比稳态量要大得多,暂态电容电流看作为如下两个电流之和:
1) 故障相电压突降而引起的放电电容电流通过母线流入故障点,其电流值衰减较快.
2) 非故障相电压突然升高而引起的充电电容电流由于其流通回路电感较大会衰减较慢.
中性点经消弧线圈接地系统发生单相接地故障后的暂态等值电路如图 2所示.图中R0为零序网络中等值电阻(包括线路及绝缘电阻)以及3倍故障点接地电阻;C0为三相对地电容之和;L0为线路及电源变压器的零模等值电感;u0为故障点零序电压;kRL、kL为消弧线圈的电阻和电感;k为当前工作档位匝数比.

|
图 2 中性点经消弧线圈接地系统的暂态等值电路 Figure 2 Transient equivalent circuit of single-phase earth fault for neutral grounded by arc suppression coil |
1) 暂态电容电流计算.由于消弧线圈的电感远大于系统线路及电源变压器的等值电感L0(L>>L0),因此在分析暂态电容电流时可不考虑消弧线圈支路(L、RL)的作用,计算暂态电容电流的微分方程为
对于架空线路的金属性接地系统和小电流接地故障,由于L0较大,C0较小,一般满足
2) 暂态电感电流的计算.计算电感线圈暂态电流可不考虑暂态电容电流影响,调匝前消弧线圈两端的电压方程为
中性点经消弧线圈接地系统发生单相接地故障后,调匝前的暂态电流为上面计算出的暂态电容电流和电感电流之和,
| $ i = {i_L} + {i_C} = \left( {\omega {C_0}{U_m} - {I_{Lm}}} \right)\cos \left( {\omega t + \varphi } \right) + {I_{Lm}}\cos \varphi {{\rm{e}}^{ - \frac{t}{{{\tau _L}}}}} + \omega {C_0}{U_m}\left( {\left( {\omega '/\omega } \right)\sin \varphi \sin \omega 't -\\ \cos \varphi \cos \omega 't} \right){{\rm{e}}^{ - \delta t}}. $ |
设在t≤ΔT时刻进行调匝,调匝后两端电压方程为
调匝后的消弧线圈电流为
| $ \begin{array}{l} i = {{i'}_L} + {i_C} = \left[ {{{I'}_{Lm}}\cos \left( {\omega t + \varphi } \right) + {{i'}_L}\left( {{0_ + }} \right)} \right]{{\rm{e}}^{ - \frac{t}{{{\tau _L}}}}} - {{I'}_{Lm}}\cos \left( {\omega t + \varphi } \right) + \\ \omega {C_0}{U_m}\left( {\left( {\omega '/\omega } \right)\sin \varphi \sin \omega 't - \cos \varphi \cos \omega 't} \right){{\rm{e}}^{ - \delta t}}. \end{array} $ |
系统仿真中电源变压器一、二次侧电压为110 kV/10 kV,用Y/Y连接方式,线路长度分别为Line1:50 km,Line2:35 km.线路每公里正序电阻为0.012 73 Ω,感抗为0.933 7 mH,容抗为12.74 nF;线路每公里零序电阻为0.386 4 Ω,感抗为4.126 4 mH,容抗为7.751 nF.
仿真时,在t=1 s时,Line2中距离母线10 km处发生A相接地故障,故障接地方式为金属性接地,接地电阻取1 Ω,发生接地故障4 s后,消弧线圈完成调压动作.仿真得到的整个变化过程的三相电压变化波形、消弧线圈电流iL、接地电流iE如图 3~5所示,图中1~5 s时间段所呈现的波形为单相接地后消弧线圈不参与调节时的电压与电流变化波形.
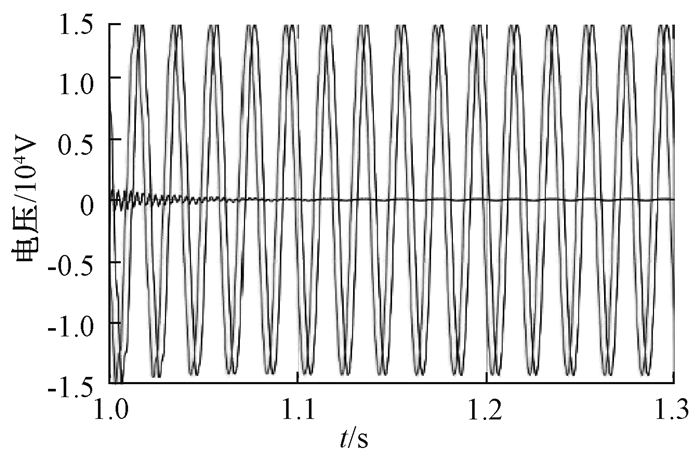
|
图 3 全过程三相电压变化波形 Figure 3 Three phase voltage change waveform in the process of adjustment |
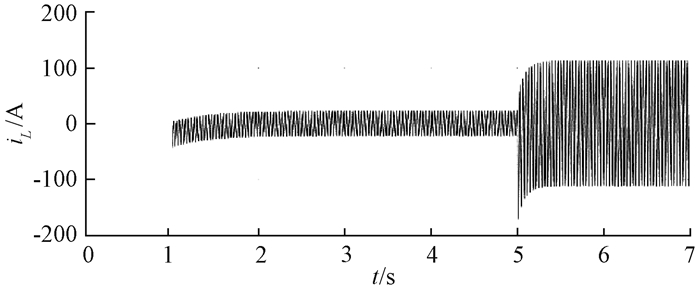
|
图 4 全过程消弧线圈电流变化波形 Figure 4 Current waveform of arc suppression in the process of adjustment |
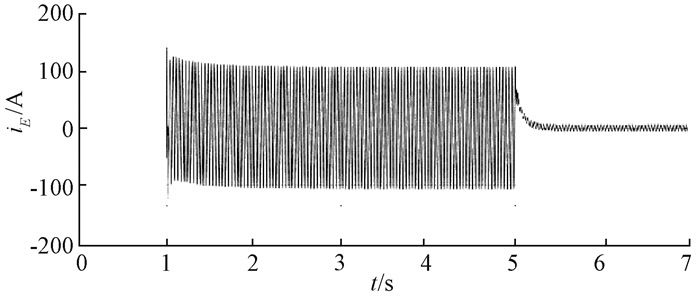
|
图 5 全过程接地电流变化波形 Figure 5 Grounding current waveform in the process of adjustment |
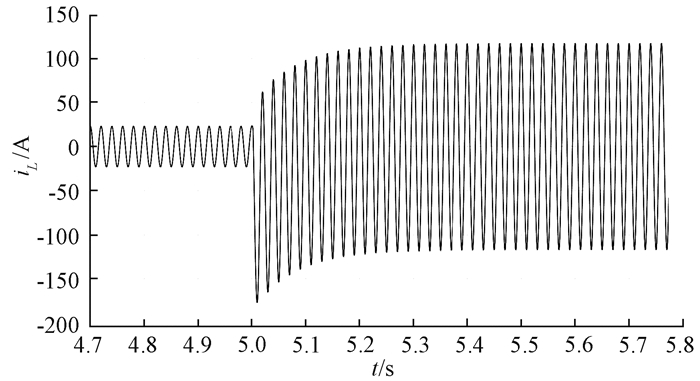
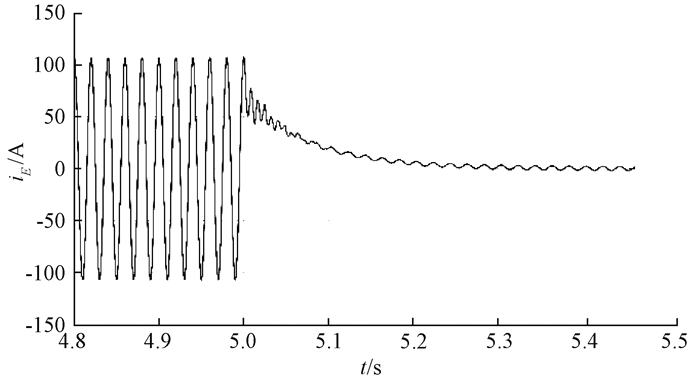
消弧线圈调匝动作完成前后消弧线圈电流iL、接地电流iE的暂态变化波形如图 6~7所示.
|
图 6 调匝前后消弧线圈电流变化波形 Figure 6 Current waveform of arc suppression coil before and after adjusting turns |
|
图 7 调匝前后接地电流变化波形 Figure 7 Grounding current waveform before and after adjusting turns |
通过以上对调匝式消弧线圈接地系统发生单相接地故障时的暂态特性分析和仿真实例分析,可以得出如下结论:
1) 系统未发生单相接地故障时,消弧线圈两端电压接近于零.
2) 发生单相接地故障后,系统接地前后参数发生变化,该变化会引起消弧线圈发生调匝动作,调匝动作完成前后通过消弧线圈的电流以及接地点电流会发生变化,调匝动作完成后通过接地点的电流很小,调匝动作引起的接地相电压改变很小,可忽略.
3) 在系统发生单相接地故障后以及消弧线圈调匝动作完成后的瞬间会出现暂态变化的电流,由于消弧线圈调匝动作一般需要数秒才能完成,在进行调匝时刻出现的暂态电流通常接近与稳态值,调匝完成后会再引起一次暂态电流变化.
4) 计及消弧线圈调匝动作时,接地故障的暂稳态特性分析需要两个阶段来进行,即调匝前暂稳态分析、调匝后暂稳态分析.
| [1] |
徐铮, 袁振海, 李春. 调匝式消弧线圈调谐原理的新研究[J]. 电气应用, 2008, 27(10): 57-60. (  0) 0) |
| [2] |
陈柏超. 新型可控饱和电抗器理论及应用[M]. 武汉: 武汉水利电力大学出版社, 1999: 210-223.
(  0) 0) |
| [3] |
王异凡, 陈国柱, 张曙. 一种连续磁阀式消弧线圈及其数学模型[J]. 电工技术学报, 2014, 25(9): 239-245. DOI:10.3969/j.issn.1000-6753.2014.09.034 (  0) 0) |
| [4] |
要焕年, 曹梅月. 电力系统谐振接地[M]. 北京: 中国电力出版社, 2009: 37-38.
(  0) 0) |
| [5] |
薛永端, 李娟, 徐丙垠. 中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J]. 中国电机工程学报, 2015, 35(22): 5703-5714. (  0) 0) |
| [6] |
薛永端, 李娟, 徐丙垠. 中性点不接地系统小电流接地故障暂态等值电路的建立[J]. 中国电机工程学报, 2013, 33(34): 223-232. (  0) 0) |
| [7] |
薛永端, 冯祖仁, 徐丙垠. 中性点非直接接地电网单相接地故障暂态特征分析[J]. 西安交通大学学报, 2004, 38(2): 195-199. (  0) 0) |
| [8] |
董新洲, 毕见广. 配电线路暂态行波的分析和接地选线研究[J]. 中国电机工程学报, 2005, 23(7): 2-5. (  0) 0) |
| [9] |
齐郑, 高玉华, 杨以涵. 配电网单相接地故障区段定位矩阵算法的研究[J]. 电力系统自动化, 2010, 38(20): 159-163. (  0) 0) |
| [10] |
贾清泉, 刘连光, 杨以涵, 等. 应用小波检测故障突变特性实现配电网小电流故障选线保护[J]. 中国电机工程学报, 2001, 21(10): 78-82. DOI:10.3321/j.issn:0258-8013.2001.10.018 (  0) 0) |
| [11] |
束洪春, 刘娟, 王超, 等. 谐振接地电网故障暂态能量自适应选线新方法[J]. 电力系统自动化, 2006, 30(11): 72-76. DOI:10.3321/j.issn:1000-1026.2006.11.015 (  0) 0) |
| [12] |
朱丹, 贾雅君, 蔡旭. 暂态能量法原理选线[J]. 电力自动化设备, 2004, 24(3): 75-78. DOI:10.3969/j.issn.1006-6047.2004.03.020 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


