基于深度图的人体动作分类自适应算法

引用本文

蒋韦晔, 刘成明. 基于深度图的人体动作分类自适应算法[J]. 郑州大学学报(理学版), 2021, 53(1): 16-21.

JIANG Weiye, LIU Chengming. Adaptive Algorithm for Human Motion Classification Based on Depth Map[J]. Journal of Zhengzhou University(Natural Science Edition), 2021, 53(1): 16-21.

基金项目

国家自然科学青年基金项目(6140240)

通信作者

刘成明(1979—)，男，副教授，主要从事计算图形学、数字图像处理研究，E-mail: cmliu@zzu.edu.cn

作者简介

蒋韦晔(1995—)，男，硕士研究生，主要从事人体动作识别研究，E-mail：837384806@qq.com

文章历史

收稿日期：2019-12-26

Contents Abstract Full text Figures/Tables PDF

基于深度图的人体动作分类自适应算法

蒋韦晔, 刘成明

郑州大学软件学院河南郑州 450002

收稿日期：2019-12-26

基金项目：国家自然科学青年基金项目(6140240)

作者简介：蒋韦晔(1995—)，男，硕士研究生，主要从事人体动作识别研究，E-mail：837384806@qq.com.

通信作者：刘成明(1979—)，男，副教授，主要从事计算图形学、数字图像处理研究，E-mail: cmliu@zzu.edu.cn.

摘要：由于深度相机成本的降低，越来越多的研究人员使用RGB-D(red, green, blue and depth)视频进行人类动作识别(human activity recognition, HAR)。使用深度运动图的局部二值模式进行特征提取，利用自适应差分进化极限学习机(self-adaptive differential evolution extreme learning machine, SaDE-ELM)用于动作分类，其中隐藏节点的学习参数通过自适应差分进化的方法进行修改。为了验证所提出方法的有效性，用3个公共数据集(MSR Action3D，MSRDaily Activity3D，MSRGesture3D)进行了实验。仿真结果表明，该方法优于基于内核的极限学习机(kernel extreme learning machine, KELM)的方法。

关键词：人类动作识别深度运动图差分进化自适应差分进化极限学习机

Adaptive Algorithm for Human Motion Classification Based on Depth Map

JIANG Weiye, LIU Chengming

School of Software, Zhengzhou University, Zhengzhou 450002, China

Abstract: Due to the cost reduction of depth camera, more and more researchers began to use RGB-D (red, green, blue and depth) video for human activity recognition (HAR). The local binary pattern of deep motion map (DMM-LBP) was used for the extraction of features; a self-adaptive extreme learning machine algorithm based on different evolution algorithm (SaDE-ELM) was used for the classification of actions; and the learning parameters of hidden nodes were also modified by SaDE-ELM. In order to verify the effectiveness of the proposed method, experiments were conducted in three public datasets (MSR Action3D, MSR DailyActivity3D and MSR Gesture3D), and the results of simulation showed that this method was better than the kernel extreme learning machine (KEML).

Key words: human action recognition deep motion map differential evolution self-adaptive differential evolution extreme learning machine

0 引言

HAR可以覆盖多种应用，例如基于内容的视频分析和检索、视觉监视和人机交互。对HAR的初步研究基于RGB摄像机。然而，由于RGB摄像机的灵敏度受混乱背景和光照条件的影响，其鲁棒性较差。低成本的深度相机对基于深度HAR领域的研究产生了深远影响，在该领域中，相机拍摄的图像对照明变化和背景杂乱不敏感，从而增强了动作识别效果。

对于动作识别问题，深度运动图(deep motion map，DMM)会从输入深度数据中捕获形状和运动提示，然后将数据从3D转换为2D。DMM是3个正交笛卡尔平面上的投影深度框架之间的累积差异。文献[1]中，深度图像通过投影和累积来生成DMM定向梯度直方图(DMM-histogram of oriented gradients, DMM-HOG)特征描述符^[1]。在DMM-HOG中，对均匀间隔的单元格计算梯度方向直方图，并执行局部对比度归一化，以减少类内差异。文献[2]使用了深度运动图的局部二值模式(deep motion map-local binary pattern，DMM-LBP)特征描述符，其性能优于基于DMM-HOG的特征描述符^[2]。LBP运算简单，并且具有旋转不变性。DMM和LBP的组合提供了有效的基于块的重叠功能。特征提取后，可以使用主成分分析(principal component analysis, PCA)减小特征尺寸。对于动作分类，通常使用KELM方法，与支持向量机的多类别分类相比，它具有更好的泛化性能，并且训练时间较少，KELM模型阶数随样本数量线性增长^[3]。文献[4]使用ELM方法进行动作分类。在ELM的训练阶段未修改隐藏参数，因而可能存在许多节点，这些节点在最小化目标函数方面的贡献较小。通过优化ELM的网络参数可以提高它的性能。近年来，差分进化(differential evolution, DE)在增强ELM的性能方面已获得普遍应用。基于DE和ELM，文献[5]提出了一种称为进化极限学习机(evolutionary-extreme learning machine, E-ELM)的新算法，在该算法中，DE用于网络参数优化，并使用ELM算法计算网络的输出权重。在E-ELM中，必须通过实验手动选择DE的试验载体生成策略和控制参数。选择不适当的策略和控制参数值可能会对网络泛化性能产生不利影响。自适应的差分进化极限学习机(self-adaptive differential evolution extreme learning machine, SaDE-ELM)是一种无梯度方法，是ELM的改进版本。在自适应差分进化算法中，使用DE对ELM的隐藏节点参数进行优化，并以自适应方式选择策略和控制参数。本文结合特征选择方法、DMM-LBP的优点和SaDE-ELM分类器的自适应特性，提出了一种改进的基于深度的人体行为分类方法。

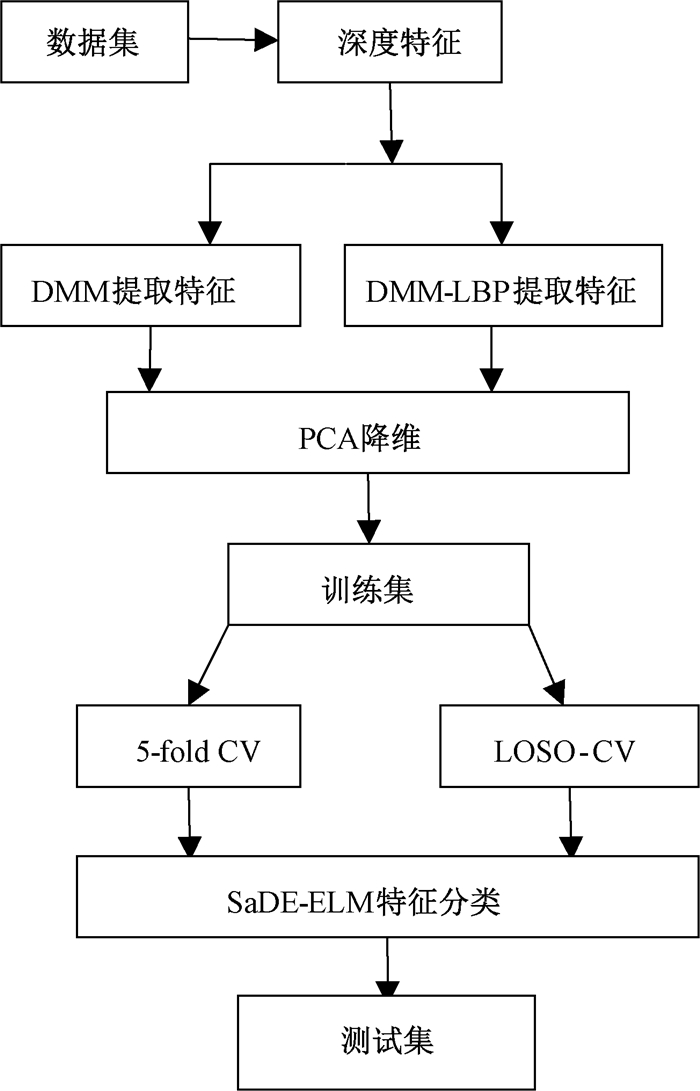
1 本文方法

HAR任务包括根据给定的输入视频自动识别动作标签。图 1显示了基于深度数据集的HAR，首先，使用DMM和DMM-LBP从深度输入中提取特征，然后通过PCA优化特征，使用SaDE-ELM方法对动作分类。我们将所提出的方法与KELM分类的性能在数据集MSR Action3D^[6]，MSRDaily Activity3D^[7]和MSRGesture3D^[8]上进行了比较。

图 1 SaDE-ELM算法流程图 Fig. 1 Flow chart of SaDE-ELM algorithm

1.1 特征提取

特征提取是将时间图像序列转换为分类器可用的特征集的过程。一般采用诸如深度图、3D关节直方图、DMM-HOG和基于骨骼的特征之类的特征提取方法，其中DMM-LBP是更加紧凑而有用的特征。对于N帧给定的深度视频，二维投影视图m_front、m_side、m_top分别对应于正面视图、侧面视图和顶视图。这些图是通过将视频帧投影到3个正交的笛卡尔平面上而生成的。计算方法为$\mathit{\boldsymbol{DM}}{\mathit{\boldsymbol{M}}_{\left\{ {{\rm{front, side, top}}} \right\}}} = \mathop \sum \limits_{k = 1}^{N - 1} \left| {\mathit{\boldsymbol{m}}_{\left\{ {{\rm{front, side, top}}} \right\}}^{k + 1} - \mathit{\boldsymbol{m}}_{\left\{ {{\rm{front, side, top}}} \right\}}^k} \right|$，其中k是帧索引。

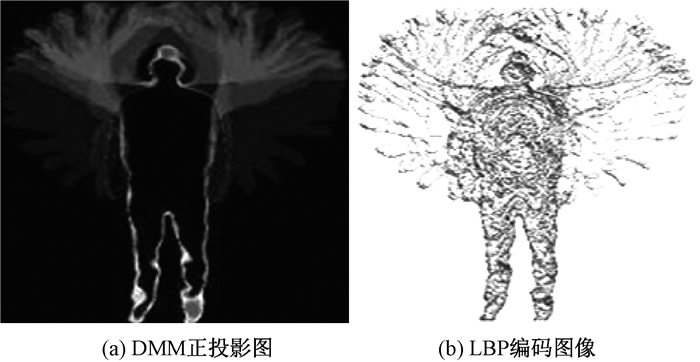
LBP是基于旋转不变纹理的算子。为了产生LBP，对具有中心像素的邻居执行阈值化。如图 2所示，用于两个手波动作的DMM序列正投影(DMM_front)和LBP编码图像。PCA由于其简单性和低噪声敏感性而被广泛用于处理高维数据^[9]，它是用原始数据的大部分方差来代替低维特征子空间。

图 2 两个手波动作的DMM的正投影图像和LBP编码图像 Fig. 2 DMM_front image and LBP coded image for the two hands wave

1.2 特征分类

分类器的目标是根据训练数据集将特征映射到动作标签。

1.2.1 ELM分类器

ELM对隐藏节点参数进行随机选择，使用等式β=L⁺T计算输出权重β，其中：T表示目标输出；L是隐藏层输出矩阵，L⁺=LT(LLT)^-1是摩尔彭罗斯L的广义逆矩阵。

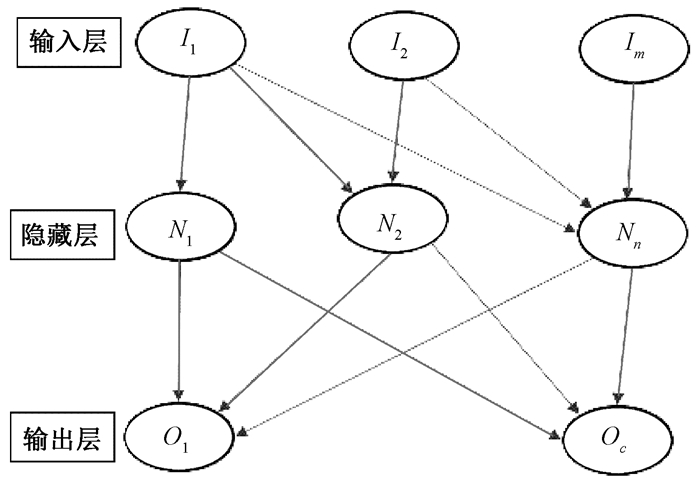
用于训练样本的单层前馈神经网络的通用ELM架构如图 3所示。其输入特征标记为{x_i，y_i}_i=1^a，I_q(q=1，…，m)表示输入层节点，N_r(r=1，…，n)表示隐藏层节点，而O_v(v=1，…，c)表示输出层节点。隐藏层输出矩阵由L=[h(x₁) h(x₂) … h(x_i)]^T表示，其中h(x_q)=g(x_q，w_r，b_r)，g(·)是非线性激活函数，w_r表示将第r个隐藏节点连接到第q个输入节点的权重向量，b_r表示第r个隐藏节点的偏置。

图 3 SLFN的极限学习机架构 Fig. 3 Extreme learning machine architecture of SLFN

当特征映射h(x_q)未知时，使用内核ELM，ELM的内核矩阵为

$ {\mathit{\boldsymbol{\lambda }}_{ELM}} = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^T}:{\mathit{\boldsymbol{\lambda }}_{EM{T_{i, j}}}} = h\left( {{\mathit{\boldsymbol{x}}_i}} \right)\dot h\left( {{\mathit{\boldsymbol{x}}_i}} \right) = R\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right), $

(1)

对于随机输入的样本x_i和x_j，R(x_i，x_j)表示给定输入的径向基函数(RBF)。

KELM算法步骤如下。

输入：动作识别训练集T；测试集T', 内核函数Ω，常数C。

输出：KELM网络的输出用于测试集T'的输出。

1) 根据文献[10]中的方法初始化内核参数。

2) 使用式(1)计算隐藏层输出。

3) 使用公式${f_r}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \left[ {R\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_{\rm{1}}}} \right) \cdots R\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_a}} \right)} \right]{\left( {\frac{1}{C} + {\mathit{\boldsymbol{\lambda }}_{ELM}}} \right)^{ - 1}}\mathit{\boldsymbol{T}}$计算输出。

4) 将标签分配给测试样品。

1.2.2 SaDE-ELM分类器

对于全局优化，DE是进化算法类别中的强大技术。由于DE使用简单、控制参数数量少、空间复杂度低、性能高和收敛速度快等优点，该方法已被广泛用于SLFN的参数优化。通过使用自适应差分进化算法^[11]，可以避免在DE中手动选择试验向量生成策略及其相关的控制参数。

SaDE-ELM算法步骤如下。

输入：数据集，总体大小，隐藏节点数。

输出：权重和最小误差。

初始化：设置索引代数G=0，随机初始化NP 个个体。

1) 使用公式$p{r_{l, G}} = \left\{ \begin{array}{l} \;\;\;\;1/4\;\;\;\;{\rm{}}\;\;\;\;\;\;{\rm{if}}\;\;\;G \Leftarrow LP{\rm{ }}\\ {S_{l, G}}/\mathop \sum \limits_{l = 1}^4 {S_{l, G}}\;\;\;\;{\rm{otherwise}} \end{array} \right.$，为每个目标向量选择一种策略。

2) 生成一个新的组，其中每个试验向量都是基于目标向量生成的策略。

3) 如果有任何变量超出定义的边界，则重新初始化试验向量。

4) 用公式${\theta _{k,G + 1}} = \left\{ {\begin{array}{*{20}{l}} {{u_{p,G + 1}}\;\;\;\;{\rm{if}}RMS{E_{{\theta _{p,G}}}}RMS{E_{{u_{p,G + 1}}}} > \in \cdot RMS{E_{{\theta _{p,G}}}},}\\ {{u_{p,G + 1}}\;\;\;{\rm{if}}\;\;\left| {RMS{E_{{\theta _{p,G}}}} - RMS{E_{{u_{p,G + 1}}}}} \right|{\rm{ ＜ }} \in \cdot RMS{E_{{\theta _{p,G}}}},}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{and}}\;\;\;\;\left\| {{\beta _{{u_{p,G + 1}}}}{\rm{ ＜ }}{\beta _{{\theta _{p,G}}}}} \right\|,}\\ {{\theta _{p,G}}\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}},} \end{array}} \right.$最小化ELM的目标函数。

公式θ_{p, G}=[ω_{1, (p, G)}^T, …, ω_{n, (p, G)}^T, b_{1, (p, G)}, …, b_{n, (p, G)}]给出了第一代总体θ的初始化，其中：权重w和偏差b是NP向量的随机分配参数；n表示隐藏节点的数量；p=1, 2, …，NP；G表示代数。

输出权重β_{p, G}用式β_{p, G}= L_{p, G}⁺T计算，L_{p, G}⁺是L_{p, G}的广义逆矩阵。RMSE用式

$ RMS{E_{p,G}} = \sqrt {\frac{{\sum\limits_{i = 1}^a {\left\| {\sum\limits_{j = 1}^n {{\beta _{jg}}} ({\omega _{(j,(p,G))}},{b_{(j,(p,G))}},{I_i}) - {t_i}} \right\|} }}{{c*a}}} $

来计算，其中：a表示训练样本的数量；c表示总类数和; t_i表示目标输出。

根据概率pr从目标向量生成实验向量，对于选择策略l(l={1，2，3，4})，S_{L, G}由下式给出，

$ {S_{l, G}} = (\mathop \sum \limits_{g = GLP}^{G1} {S_{l, g}})/(\mathop \sum \limits_{g = GLP}^{G1} S{S_{l, g}} + \mathop \sum \limits_{{\rm{ }}g = GLP}^{G1} {f_{l, g}}) + \in , $

其中：l表示策略；g表示生成；f_{l, g}表示在下一代中丢弃的g^th和l^th策略处的试验向量的数量。

2 实验设置及实验分析

实验是在MSR Action3D，MSRDaily Activity3D和MSRGesture3D公开获得的数据集上进行的。

2.1 实验设置

所有实验均在Matlab 2016b上进行。DMM-LBP参数设置类似于文献[10]。在提取DMM并计算LBP之后，使用PCA降低数据集的维数。表 1给出了平均特征大小和降维后的平均特征大小。分类任务由SaDE-ELM算法执行。SaDE-ELM方法的参数选择为20，下界和上限设置为-1和1，最大世代数为60，隐藏节点数为80。专门针对特定的训练数据进行了5折交叉验证和"遗漏一名受试者"(LOSO)。在5-fold CV(5折交叉验证)中，从10名随机选择的受试者中选择5名进行训练，休息时进行测试。

表 1 特征描述 Tab. 1 Feature description

2.2 实验结果及分析

混淆矩阵用于根据精确率、召回率、f值和准确率评估所提出方法的性能，计算公式为Precison=TP/(TP+FP)，Recall=TP/(TP+FN)，f-score=(2*precision*recall)/(precision+recall)，Accuracy=(TP+TN)/(TP+TN+FP+FN)，准确率和召回率是使用"真阳性"(TP)，"假阳性"(FP)和"假阴性"(FN)来计算的，这些值指示正确分类的操作数。被错误标记为肯定类别的操作数，动作应分别标记为肯定类，但错误地标记为否定类的操作数。

表 2和表 3分别提供了MSRGesture3D、MSR Action3D和MSRDaily Activity3D数据集的5-fold CV(5折交叉验证)和LOSO结果。在表 2和表 3中，EAP1、P-AP1、E-AP2和P-AP2对应于由DMM-KELM、DMM-SaDE-ELM，现有方法DMM-LBP-KELM和提出的方法DMM-LBP-SaDE-ELM。我们对方法E-AP1和P-AP1，E-AP2和P-AP2进行了成对比较。从结果中可以看出，与现有方法相比，该方法的中值精确率提高了1%~15%。我们使用Wilcoxon符号秩检验对获得的结果进行了统计分析。对于成对比较(E-AP1，P-AP1、E-AP2和P-AP2), 测试数据集DS1(MSRGesture3D)、DS2(MSR Action3D)和DS3(MSRDaily)Activity3D)得出的p值小于0.05，表明我们提出的方法比现有方法具有更好的性能。所提方法的性能与文献[10]中提出的方法在精确率、准确率、召回率和f值方面进行了比较。表 2和表 3列出了3个基于深度模态的数据集(包括手势、动作和活动)的这些性能指标的最小值、最大值、平均值和中值。

表 2 5-fold CV下的实验结果 Tab. 2 Experimental results under 5-fold CV

单位:%
方法	准确率				精确率				召回率				f值
5-fold	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值
E-AP1 DS1	53	77	68	69	56	80	71	71	53	77	68	68	59	81	73	73
E-AP1 DS1	57	81	71	72	59	83	74	74	58	81	71	72	62	84	75	75
E-AP2 DS1	72	94	82	81	72	95	83	88	70	94	81	88	75	95	83	89
E-AP2 DS1	73	95	86	87	75	95	87	88	71	94	85	89	73	94	86	89
E-AP1 DS2	68	87	79	81	70	89	82	82	68	86	77	78	79	89	84	88
E-AP1 DS2	72	90	80	83	75	90	82	82	72	89	80	88	79	91	85	85
E-AP2 DS2	76	95	85	88	79	95	87	89	76	94	85	85	84	96	89	90
E-AP2 DS2	82	95	87	88	81	95	88	89	79	94	87	89	84	97	89	88
E-AP1 DS3	21	48	35	36	13	54	31	31	17	38	28	29	39	71	57	58
E-AP1 DS3	33	54	44	47	25	64	40	39	28	48	37	38	43	77	60	60
E-AP2 DS3	49	56	49	54	37	59	48	47	41	55	49	48	58	80	68	67
E-AP2 DS3	50	58	52	53	44	60	51	53	45	58	52	51	58	81	70	71

表 2 5-fold CV下的实验结果 Tab. 2 Experimental results under 5-fold CV

表 3 LOSO CV下的实验结果 Tab. 3 Experimental results under LOSO CV

单位:%
方法		准确率				精确率				召回率				f值
LOSO	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值	最小值	最大值	平均值	中值
E-AP1 DS1	50	94	77	78	54	95	77	78	50	94	77	78	63	94	86	90
E-AP1 DS1	67	97	85	84	72	98	86	88	67	97	85	85	74	98	91	92
E-AP2 DS1	68	100	87	88	68	100	88	88	68	100	87	86	81	100	94	94
E-AP2 DS1	77	100	94	96	75	100	94	97	77	100	95	95	84	100	97	98
E-AP1 DS2	64	95	84	86	66	91	83	88	61	92	83	86	82	98	92	93
E-AP1 DS2	79	100	93	94	74	100	92	96	77	100	92	94	88	100	96	97
E-AP2 DS2	81	98	92	92	81	99	91	91	82	98	91	91	92	99	96	96
E-AP2 DS2	88	100	97	96	88	100	95	98	89	100	95	97	94	100	98	99
E-AP1 DS3	31	58	46	47	26	51	40	39	31	57	46	46	63	87	77	77
E-AP1 DS3	56	66	62	62	52	69	62	63	56	66	62	62	74	91	82	82
E-AP2 DS3	47	68	60	62	44	74	58	58	53	68	61	62	75	94	85	85
E-AP2 DS3	67	80	70	73	65	80	71	68	67	81	73	75	81	93	87	87

表 3 LOSO CV下的实验结果 Tab. 3 Experimental results under LOSO CV

考虑到表 2和表 3的中位数精度测度，提出的仅使用带有SaDE-ELM分类器的DMM功能的方法的性能要优于DMM-ELM方法。结合DMM和LBP功能比仅DMM功能具有显著的性能改进，因为与DMM功能相比，它可以生成紧凑的功能，并可以增强图像的边缘。与使用ELM分类器相比，使用SaDE-ELM方法优化前馈网络的隐层权重和偏差，可以使准确性性能的中位数提高1%~15%(使用成对比较)。这是因为初始化参数是在ELM算法中随机生成的，这对输出权重矩阵有重大影响。为了改进ELM算法，采用优化的DE算法(SaDE-ELM)自适应地收集DE算法的未知参数，从而提高了HAR的准确性。

3 结束语

本文提出了一种通用的HAR方法，该方法已应用于动作、活动和手势等模态。针对基于深度的视频提出了一种改进的动作识别方法，包括特征提取、特征组合、特征选择和动作分类。由于DMM-LBP特征的紧凑性和旋转不变性，我们采用了DMM-LBP特征的组合。对于特征选择，我们使用了主成分分析(PCA)。对于动作分类，我们使用了SaDE-ELM方法。在SaDE-ELM方法中，采用基于DE的自适应控制参数，优化前馈网络的隐节点参数，并利用ELM算法确定网络输出权值。该方法不仅利用了ELM较好的泛化性能，而且利用自适应DE为SLFN获得了合适的权重和偏差。我们在3个公开可用的数据集上将该方法与KELM方法的性能进行了比较。

由于多模态数据将基于人和对象之间的交互来细化动作分类任务，因此可以将来自输入视频的多模态数据(骨骼+深度)用于动作识别，作为将来的工作，由于深层网络会自动从视频中提取特征，因此使用深层CNN进行人体行为分类，可以被认为是另一项未来的工作。该工作还可以扩展到数据集，包含从多个摄像机捕获的多个视图。

参考文献

[1]	YANG X, ZHANG C, TIAN Y. Recognizing actions using depth motion maps-based histograms of oriented gradients[C]//Proceedings of the 20th ACM International Conference on Multimedia. New York, 2012: 1057-1060. (0)
[2]	程万里.基于深度数据特征融合的人体动作识别[D].郑州: 郑州大学, 2018. CHENG W L. Human action recognition based on depth data feature fusion[D]. Zhengzhou: Zhengzhou University, 2018. (0)
[3]	WONG C M, VONG C M, WONG P K, et al. Kernel-based multilayer extreme learning machines for representation learning[J]. IEEE transactions on neural networks and learning systems, 2018, 29(3): 757-762. DOI:10.1109/TNNLS.2016.2636834 (0)
[4]	王杰, 刘向晴. 彩色图像分割的FCM预分类核极限学习机方法[J]. 郑州大学学报(理学版), 2018, 50(2): 75-80. WANG J, LIU X Q. FCM pre-classification kernel extreme learning machine algorithm of color image segmentation[J]. Journal of Zhengzhou university(natural science edition), 2018, 50(2): 75-80. (0)
[5]	ZHU Q Y, QIN A K, SUGANTHAN P N, et al. Evolutionary extreme learning machine[J]. Pattern recognition, 2005, 38(10): 1759-1763. DOI:10.1016/j.patcog.2005.03.028 (0)
[6]	MSRaction3D dataset. (2018-01-05)[2019-02-10]. http://research.microsoft.com/enus/um/people/zliu/actionrecorsrc/. (0)
[7]	MSRdailyActivity3D dataset. (2018-09-07)[2019-02-10]. http://users.eecs.northwestern.edu/~jwa368/my_data.html. (0)
[8]	DING W W, LIU K, FU X J, et al. Profile HMMs for skeleton-based human action recognition[J]. Signal processing: image communication, 2016, 42: 109-119. DOI:10.1016/j.image.2016.01.010 (0)
[9]	KARAMIZADEH S, ABDULLAH S M, MANAF A A, et al. An overview of principal component analysis[J]. Journal of signal and information processing, 2013, 4(3): 173-175. DOI:10.4236/jsip.2013.43B031 (0)
[10]	CHEN C, JAFARI R. Action recognition from depth sequences using depth motion maps-based local binary patterns[C]//2015 15th IEEE Winter Conference on Applications of Computer Vision. Waikoloa, 2015: 1092-1099. (0)
[11]	NUNES U M, FARIA D R, PEIXOTO P. A human activity recognition framework using max-min features and key poses with differential evolution random forests classifier[J]. Pattern recognition letters, 2017, 99: 21-31. DOI:10.1016/j.patrec.2017.05.004 (0)