分数阶微积分有着广阔的应用领域和前景,如生物传热、粘弹性力学、图像信号和风力发电等.由于求分数阶微积分方程的解析解存在诸多困难,所以重点研究它的数值解.目前微积分方程的数值解法较多,如有限差分法[1]、有限元法[2]、小波方法[3]、拉格朗日乘子法[4]、变分迭代法[5]、同伦摄动法[6]等,也有与统计力学相结合的随机行走方法[7]等.上述方法较多研究整数阶微积分方程,而分数阶微积分方程更复杂,精确数值模拟分数阶微积分方程的困难更大,现有文献中研究分数阶微积分方程数值解的理论较少,而且很少考虑计算精度或收敛速度等问题.高精度无网格重心插值配点法是一种新型求解分数阶积分方程的数值方法[8],该方法相对其他数值方法而言应用前景广阔,克服了一般插值方法的振荡性和向前稳定性,具有计算精度高,不用划分网格,程序容易实现等诸多优点.重心插值配点法多用于数值模拟积分微分方程和偏微分方程.文献[9]运用线性重心有理插值配置法求解了一阶线性双曲型初值边值问题.文献[10]运用两种重心型插值求解了带初值问题和边值问题的二阶线性微分方程,并将重心插值法与拟谱法以及微分求积法做了比较,得出重心插值法比其他数值方法精度更高.文献[11]使用直接线性重心有理插值(DRQ)求解了线性Fredholm积分函数,用间接线性重心有理插值法(IRQ)求解了线性Volterra积分函数,并给出了误差估计,从而说明了重心插值法的高效性.
与以往插值配点法不同,本文将运用重心插值配点法求解分数阶Fredholm积分方程,从而推导出分数阶Fredholm积分方程重心插值配点法的离散计算公式.通过证明解的存在唯一性、误差估计以及数值算例验证本文方法的高精度和可靠性.
1 重心插值配点法设xj(j=0, 1, …, n+1) 是函数f(x)的n+1个不同的插值节点,其对应的函数值为fj.如果要使用多项式插值,则可以在多项式空间中求插值多项式p(x),使得p(xj)=fj, j=0, 1, …, n,而多项式空间的次数不超过n.
定义 1[12] 重心Lagrange插值公式
| $ p\left( x \right) = \left( {\sum\limits_{j = 0}^n {\frac{{{\omega _j}}}{{x - {x_j}}}{f_j}} } \right)/\left( {\sum\limits_{j = 0}^n {\frac{{{\omega _j}}}{{x - {x_j}}}} } \right) = \sum\limits_{j = 0}^n {{L_j}\left( x \right){f_j}} , $ | (1) |
式中Lj(x)为Lagrange插值基函数,其表达形式为
| $ {\omega _j} = 1/\prod\limits_{j \ne k}^n {\left( {{x_j} - {x_k}} \right)} ,\;\;\;j = 0,1, \cdots ,n. $ | (2) |
由式(1) 可知, 分子和分母都包含重心权ωj, 由式(2) 可知, 重心权只依赖于插值节点的分布,因此插值节点直接影响着重心权.本文主要采用等距节点和第二类Chebyshev节点来研究分数阶积分方程的数值解.
2 分数阶积分方程定义 2[13] 设函数f(t)为定义在
本文主要探讨如下形式的分数阶Fredholm积分方程,
| $ f\left( x \right) - \frac{1}{{\Gamma \left( \alpha \right)}}\int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}K\left( {x,t} \right)f\left( t \right){\rm{d}}t} = g\left( x \right),\;\;\;x \in \left[ {a,b} \right],\alpha > 0, $ | (3) |
其中:f(x)为未知函数;g(x)∈C[a, b]为已知函数;K(x, t)为区间[a, b]×[a, b]上的、关于变量x, t的二元连续积分核函数.将积分方程的积分区间[a, b]离散为a=x0 < x1 < x2 < … < xn=b,则令未知函数f(x)在离散节点x0, x1, x2, …, xn上的函数值为f0, f1, f2, …, fn,记fi=f(xi), i=0, 1, 2, …, n.用重心型插值来近似未知函数f(x),
| $ f\left( x \right) = \sum\limits_{j = 0}^n {{L_j}\left( x \right){f_j}} , $ | (4) |
式中
| $ \sum\limits_{j = 0}^n {{L_j}\left( x \right){f_j}} - \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {\left[ {\int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {x,t} \right){L_j}\left( t \right){\rm{d}}t} } \right]{f_j}} = g\left( x \right), $ | (5) |
令方程(5) 在节点x0, x1, x2, …, xn上均成立,可得
| $ \sum\limits_{j = 0}^n {{L_j}\left( {{x_i}} \right){f_j}} - \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {\left[ {\int_a^b {{{\left( {{x_i} - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {{x_i},t} \right){L_j}\left( t \right){\rm{d}}t} } \right]{f_j}} = g\left( {{x_i}} \right), $ | (6) |
令
| $ \sum\limits_{j = 0}^n {\left[ {\int_a^b {{{\left( {{x_i} - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {{x_i},t} \right){L_j}\left( t \right){\rm{d}}t} } \right]} = \sum\limits_{j = 0}^n {{\mathit{\boldsymbol{K}}_j}\left( {{x_i}} \right)} , $ |
其中
| $ \sum\limits_{j = 0}^n {{L_j}\left( {{x_i}} \right){f_j}} - \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {{\mathit{\boldsymbol{K}}_j}\left( {{x_i}} \right){f_i} = g\left( {{x_i}} \right)} ,\;\;\;i = 0,1,2, \cdots ,n. $ | (7) |
将式(7) 写成矩阵形式为
| $ \left( {\mathit{\boldsymbol{I}} - \frac{1}{{\Gamma \left( \alpha \right)}}\mathit{\boldsymbol{K}}} \right)\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{G}}. $ | (8) |
其中:K=[Kij]:=[Kj(xi)]为未知函数f(x)在节点x0, x1, x2, …, xn的积分矩阵;I为n阶单位矩阵;F=[f(x0), f(x1), f(x2), …, f(xn)]T为f(x)在插值点处函数值;G=[g(x0), g(x1), g(x2), …, g(xn)]T为自由项g(x)所对应的插值点处的函数值.这样式(8) 就给出了积分方程(3) 的重心插值配点法的离散计算公式.
由Gauss公式[14],对给定的xi有
| $ {\mathit{\boldsymbol{K}}_j}\left( {{x_i}} \right) = \int_a^b {\left( {{{\left( {{x_i} - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {{x_i},t} \right){L_j}\left( t \right)} \right){\rm{d}}t} = \frac{{b - a}}{2}\sum\limits_{k = 1}^q {{{\left( {{x_i} - {t_k}} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {{x_i},{t_k}} \right){L_j}\left( {{t_k}} \right){A_\mathit{\boldsymbol{k}}}} . $ |
其中:tk, Ak分别为Gauss求积公式的积分点和积分权;q为积分点的数量,(b-a)/2为定积分的变换系数. Gauss求积公式是一种机械型求积方法,这类方法将积分求值问题转化为函数值的计算问题,积分权Ak紧密依赖于积分点tk的选取,与被积函数f(x)的形式没有关系,而积分点tk的数量q可以直接影响数值结果的好坏,当q越大计算误差越小,当q达到一定数量时,继续增加q对计算误差的影响将变小,但计算时间会变大,故可根据实际问题的需要适当选取q.
4 误差分析 4.1 解的存在唯一性引理 1[15] (Fredholm选择定理)第二类Fredholm积分方程,要么对于所有函数f(x)都有解且解唯一,要么相应的齐次方程至少有一个非平凡解,即至少有一个不恒等于零的解.
引理 2[16] (压缩映射原理)设(X, d)是完备的距离空间,T:X→X是压缩映射.则T在X中存在唯一的不动点x0.
由引理1可知,本文所研究的方程必然有解.在Banach空间中,设核K(x, t)在矩形区域D1=[a, b]×[a, b]上连续,自由项g(x)∈C[a, b],下面利用压缩映射原理(引理2) 证明其解的唯一性.
定理 1 方程(3) 存在唯一解,当且仅当
证明 定义映射T为
| $ Tf\left( x \right) = g\left( x \right) + \frac{1}{{\Gamma \left( \alpha \right)}}\int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {x,t} \right)f\left( t \right){\rm{d}}t} , $ |
则T:C[a, b]→C[a, b], 由于x-t>0, 从而(x-t)α-1>0, 且对于任意的f1, f2∈C[a, b],有
| $ \begin{array}{l} \left\| {T{f_1} - T{f_2}} \right\| = \mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {T{f_1}\left( x \right) - T{f_2}\left( x \right)} \right| \le\\ \frac{1}{{\Gamma \left( \alpha \right)}}\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|\left| {\left( {{f_1}\left( t \right) - {f_2}\left( t \right)} \right)} \right|{\rm{d}}t} \le \\ \frac{1}{{\Gamma \left( \alpha \right)}}\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {{f_1}\left( t \right) - {f_2}\left( t \right)} \right|\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} = \\ \frac{1}{{\Gamma \left( \alpha \right)}}\left\| {{f_1} - {f_2}} \right\|\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left( {\int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} } \right) = \frac{M}{{\Gamma \left( \alpha \right)}}\left\| {{f_1} - {f_2}} \right\|, \end{array} $ |
式中令
本文主要采用两种范数误差来刻画数值解与精确解的逼近程度问题,其中
下面主要运用
定理2 设
| $ M = \mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} ,\omega \left( x \right) = \prod\limits_{i = 0}^n {\left( {x - {x_i}} \right)} ,\xi \in \left[ {a,b} \right]. $ |
证明 设
| $ \begin{array}{l} \left\| {f\left( x \right) - \tilde f\left( x \right)} \right\| = \left\| {\frac{1}{{\Gamma \left( \alpha \right)}}\int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\mathit{\boldsymbol{K}}\left( {x,t} \right)\left( {f\left( t \right) - \tilde f\left( t \right)} \right){\rm{d}}t} } \right\| \le \\ \frac{1}{{\Gamma \left( \alpha \right)}}\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|\left( {f\left( t \right) - \tilde f\left( t \right)} \right){\rm{d}}t} \le \\ \frac{1}{{\Gamma \left( \alpha \right)}}\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {f\left( t \right) - \tilde f\left( t \right)} \right|\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} , \end{array} $ | (9) |
重心Lagrange插值公式(1) 可以写为
若f(x)在[a, b]上存在n+1阶导数,则对
| $ \left| {f\left( x \right) - \tilde f\left( x \right)} \right| \le \frac{{\omega \left( x \right)}}{{Q\left( x \right)}} \cdot \frac{{\left[ {f\left( x \right)Q\left( x \right) - P\left( x \right)} \right]_{x = \xi }^{\left( {n + 1} \right)}}}{{\left( {n + 1} \right)!}}, $ | (10) |
其中:
| $ \begin{array}{l} \left\| {f\left( x \right) - \tilde f\left( x \right)} \right\| \le \frac{1}{{\Gamma \left( \alpha \right)}}\mathop {\max }\limits_{t \in \left[ {a,b} \right]} \left| {f\left( x \right) - \tilde f\left( x \right)} \right|\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} \le \\ \frac{1}{{\Gamma \left( \alpha \right)}}\frac{{\omega \left( x \right)}}{{Q\left( x \right)}}\frac{{\left[ {f\left( x \right)Q\left( x \right) - P\left( x \right)} \right]_{x = \xi }^{\left( {n + 1} \right)}}}{{\left( {n + 1} \right)!}}\mathop {\max }\limits_{t \in \left[ {a,b} \right]} \int_a^b {{{\left( {x - t} \right)}^{\alpha - 1}}\left| {\mathit{\boldsymbol{K}}\left( {x,t} \right)} \right|{\rm{d}}t} \le \\ \frac{{\omega \left( x \right)M}}{{Q\left( x \right)\Gamma \left( \alpha \right)}}\frac{{\left[ {f\left( x \right)Q\left( x \right) - P\left( x \right)} \right]_{x = \xi }^{\left( {n + 1} \right)}}}{{\left( {n + 1} \right)!}}. \end{array} $ |
证毕.
5 数值算例为了验证本文方法的高精度和可靠性,对2个具有精确解的数值算例进行数值模拟.算例中均分别选取等距节点和第二类Chebyshev节点,并对这两种节点下数值结果的
算例1
| $ f\left( x \right) - \frac{1}{{\Gamma \left( \alpha \right)}}\int_0^1 {xt{{\left( {x - t} \right)}^{\alpha - 1}}f\left( t \right){\rm{d}}t} = g\left( x \right),\;\;\;x \in \left[ {0,1} \right], $ |
当α=1,取g(x)=11x/(12-x2)时, 该分数阶方程退化为整数阶积分方程,精确解为f(x)=x(1-x). 表 1为本文方法当α=1,n=10,q=8时两类节点和文献[18]方法的
|
|
表 1 算例1本文方法当α=1,n=10,q=8时两类节点和文献[18]方法的 |
|
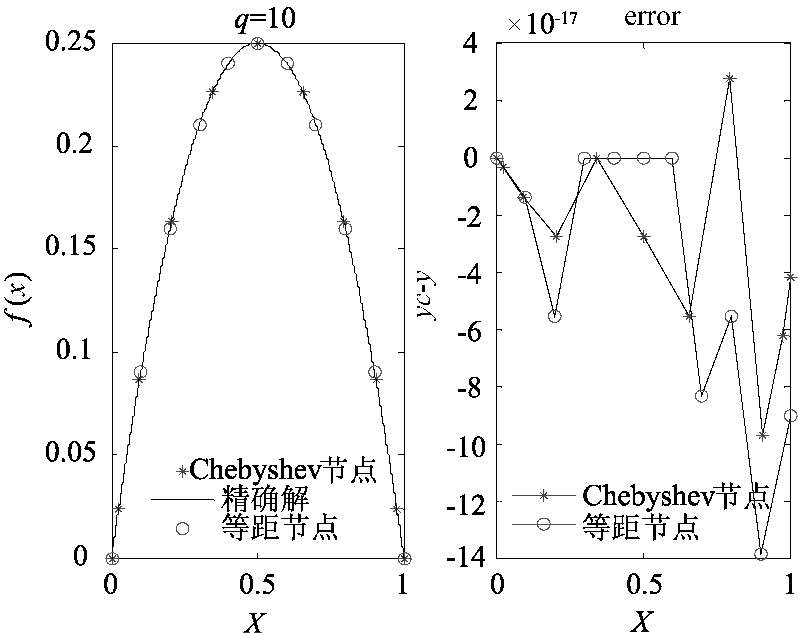
图 1 算例1当α=1,n=10,q=8时两类节点的误差与数值解精确解比较 Figure 1 The computed solution, exact solution and the error estimation with α=1, n=10, q=8 for two knots for example 1 |
|
|
表 2 算例1当α=5/2时两类节点的数值解、精确解、 |
由表 1、表 2和图 1可知,用重心插值配点法求解分数阶Fredholm积分方程时, α增大,q增大时,其计算精度随之增大.当q由10变为100时,精度增加了3个数量级,当q由100变为500时,精度增加了2个数量级,这说明q影响数值解的计算精度为, q越大计算效果越好,但相应计算时间增大.两类节点所得数值解的计算精度都比较高,其中第二类Chebyshev节点比等距节点的计算精度更高.当α=1时,算例1退化为整数阶时,q取10时相对误差达到10-16,与文献[18]的方法相比,本文方法的计算精度更高.
算例 2
| $ f\left( x \right) - \frac{1}{{\Gamma \left( \alpha \right)}}\int_0^1 {{{\rm{e}}^{x - t}}{{\left( {x - t} \right)}^{\alpha - 1}}f\left( t \right){\rm{d}}t} = g\left( x \right),\;\;\;x \in \left[ {0,1} \right]. $ |
当α=5/2时,选取适当的g(x)使算例2的精确解为f(x)=x3(1-x)ex.具体计算中,分别取11个和21个插值节点,即分为n=10和n=20两种情况,q取10.由表 3可以看出,Gauss积分点数量q相同时,n=20比n=10计算效果更好,等距节点比第二类Chebyshev节点更好.
|
|
表 3 算例2当α=5/2时两类节点的 |
综合上述2个算例可知,应用重心插值配点法求解分数阶Fredholm积分方程时,可以得到很高的计算精度.计算精度随着阶数α的增大而增大,并且也受Gauss积分点数量q与插值节点个数n的影响.当α=1,即积分方程由分数阶退化为整数阶,q与n取很小时就能得到很高的计算精度.当α≠1,α越大,q越大,n越大时,分数阶积分方程的计算精度越高.同时也可知,对于分数阶积分方程的精确解为基本初等函数时,第二类Chebyshev节点比等距节点的精度更高,对于其精确解为更加复杂的函数时,等距节点比第二类Chebyshev节点的精度更高一些.
6 小结本文应用重心插值配点法求解了分数阶第二类Fredholm积分方程,推导出了分数阶Fredholm积分方程重心插值配点法的离散计算公式,证明了本文所讨论方程的解的存在唯一性,得出了误差估计,最后利用数值算例通过对比等距节点与第二类Chebyshev节点的数值结果,验证了本文方法的高精度和可靠性,并得出影响精度的条件,也给出两类节点的适用范围.本文利用重心插值配点法对分数阶Fredholm积分方程进行了研究,得到了较好的结果.
| [1] |
丁恒飞. 分数阶偏微分方程的有限差分方法[D]. 上海: 上海大学, 2014.
(  0) 0) |
| [2] |
AGRAWAL O P. A general finite element formulation for fractional variational problems[J]. Journal of mathematical analysis and applications, 2008, 337(1): 1-12. DOI:10.1016/j.jmaa.2007.03.105 (  0) 0) |
| [3] |
HEYDARIA M H, HOOSHMANDASLM R, MOHAMMADIF, et al. Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations[J]. Communication in nonlinear science and numerical simulation, 2014, 19(1): 37-48. DOI:10.1016/j.cnsns.2013.04.026 (  0) 0) |
| [4] | |
| [5] |
HETMANIOK E, NOWAK I, STOA D, et al. A study of the convergence of and error estimation for the homotopy perturbation method for the Volterra-Fredholm integral equations[J]. Applied mathematics letters, 2013, 26(26): 165-169. (  0) 0) |
| [6] |
ZHAN J, CHEN L, FU Y, et al. A new random walk simulation model for study of diffusion behavior of single particle within two-dimensional space[J]. Journal of electrochemistry, 2012, 18(5): 427-436. (  0) 0) |
| [7] |
WU G C. A fractional variational iteration method for solving fractional nonlinear differential equations[J]. Computers and mathematics with applications, 2011, 61(61): 2186-2190. (  0) 0) |
| [8] |
王兆清, 李淑萍, 唐炳涛. 一维重心型插值:公式、算法和应用[J]. 山东建筑大学学报, 2007, 22(5): 448-453. (  0) 0) |
| [9] |
BALTENSPERGER R, BERRUT J P. The linear rational collocation method[J]. Journal of computational and applied mathematics, 2001, 134(1/2): 243-258. (  0) 0) |
| [10] |
李淑萍. 基于重心型插值的数值计算方法[J]. 山东科学, 2010, 23(4): 13-16. (  0) 0) |
| [11] |
KLEIN G, BERRUT J P. Linear barycentric rational quadrature[J]. Bit numerical mathematics, 2012, 52(2): 407-424. DOI:10.1007/s10543-011-0357-x (  0) 0) |
| [12] |
李树忱, 王兆清. 高精度无网格重心插值配点法:算法、程序及工程应用[M]. 北京: 科学出版社, 2012.
(  0) 0) |
| [13] |
OLDHAM K B, SPANIER J. The fractional calculus theory and applications of differentiation and integration toarbitrary order[M]. New York: Dover Publications Inc, 2002.
(  0) 0) |
| [14] |
李岳生, 黄友谦. 数值逼近[M]. 北京: 人民教育出版社, 1978.
(  0) 0) |
| [15] |
吕涛, 黄晋. 积分方程的高精度算法[M]. 北京: 科学出版社, 2013.
(  0) 0) |
| [16] |
匡继昌. 实分析与泛函分析[M]. 北京: 高等教育出版社, 2002.
(  0) 0) |
| [17] |
ZOU L, LI C. Barycentric Lagrange blending rational interpolation based on Padè approximation[C]//Proceeding of the 2011 International Conference on Computational and Information Sciences.Washington, 2011:1124-1127.
(  0) 0) |
| [18] |
张倩, 韩惠丽, 张盼盼. 基于有理Haar小波求解分数阶第2类Fredholm积分方程[J]. 江西师范大学学报(自然科学报), 2014, 38(1): 47-50. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


