2. 中国计量大学 信息工程学院 浙江 杭州 310000
2. College of Information Engineering, China Jiliang University, Hangzhou 310000, China
太阳能是未来清洁能源的关键,它能通过太阳能电池板产生大量电能而不会燃烧化石燃料。全球已经制定了许多能源法规和激励措施,以提高太阳能在未来智能电网中的利用率[1]。但是,太阳能的随机性和间歇性给电网的稳定运行和管理带来了困难[2]。这些不确定性也会降低实时控制性能和经济效益,不利于光伏电站的大规模扩张,因此能够准确预测光伏发电功率(photovoltaic power,PV)的预测方法已成为解决光伏发电规划和建模问题的重要工具,可以减轻对整个电力系统的负面影响,提高系统的稳定性[3]。随着当前电网中高级电表的发展,可以使用更丰富的源数据来建立更复杂的预测模型,以实现更准确的光伏发电功率预测[4]。
光伏发电的预测方法主要有统计方法、物理方法和人工智能方法。统计方法试图建立历史数据和输出功率之间的函数映射关系,例如时间序列法、回归分析方法、灰色理论。统计模型通常依赖于历史数据,并且需要排除不利于这些模型的病态数据点。与统计方法不同,物理方法不需要大量历史数据的支持,它研究了光伏发电设备的特性并建立了相应的数学模型进行功率预测,物理数学模型中使用的气象和地质参数通常通过数值天气预报或地面测量设备进行测量,但是,物理方法需要适当且经常校准的服务设施[5]。人工智能学习方法得益于计算能力的快速增长,利用人工智能算法学习输入和输出之间的映射关系,主要包括非线性映射模型[6]。人工智能方法已广泛应用于各个领域,包括异常检测、电网、能耗、模式识别,已成为预测光伏发电功率较好的工具[7]。
人工智能方法以光伏发电预测技术为核心,有效地提取了与光伏系统有关的历史数据的非线性特征,从而比统计方法和物理方法具有更强的竞争力[8]。此外,人工智能方法可以直接从易于访问的数据中预测光伏输出功率,而无须进行复杂的计算和其他高昂的成本。文献[9]提出了一种基于粒子群优化与极限学习机组合算法的短期光伏发电功率预测模型。文献[10]系统地分析了一些对建立时序预测模型产生影响的因素,设计了一种优化的网络训练方法。近年来随着深度学习的流行,深度学习方法被广泛应用于光伏发电功率预测领域,并取得了出色的成果[11]。深度学习可以自动从数据中学习有用的功能,而不是使用传统的特征选择方法。例如,文献[12]提出了一种高精度的深度神经网络模型来预测光伏系统的输出功率。此外,文献[13]建立了考虑季节天气分类的反向传播神经网络预测模型来预测光伏发电量。文献[14]提出了一种简化的方法,即通过使用径向基函数神经网络来预测光伏系统中输出功率。文献[15]开发了三种不同的人工神经网络模型来预测光伏发电量。文献[16]利用LSTM来预测光伏发电功率。
LSTM作为最重要的深度学习技术之一,在相关工作中得到广泛应用[17],但是LSTM作为单一的深度学习模型,只能提取数据的长期依赖特征。为了进一步提高LSTM的预测精度,本文提出了一种新型域融合深度模型(DWT-CNN-LSTM),通过卷积神经网络(CNN)和离散小波变换(DWT)提取数据的时域和频域特征,再通过长短期记忆神经网络(LSTM)提取其长期依赖特征,以准确地完成预测。
1 基本概念 1.1 小波变换小波变换包括连续小波变换(continuous wavelet transform,CWT)和离散小波变换(DWT)。与CWT相比,DWT可以节省时间和计算资源,同时保持较低的重构误差。因此本文采用DWT分解功耗序列,表示为
| $ D W T(x(t))_{a, b}=\int_{-\infty}^{+\infty} x(t) D W_{a, b}(t) \mathrm{d} t, $ | (1) |
其中:DWT是输入信号x(t)与一组离散小波DWa, b(t)的积分;比例因子为a;时间局部化为b;
| $ D W_{a, b}(t)=\frac{1}{\sqrt{a}} \varphi\left(\frac{t-b}{a}\right),\left\{\begin{array}{l} a=2^{j}, j \in {\bf{Z}} \\ b=k 2^{j}, j, k \in {\bf{Z}} \end{array},\right. $ |
其中φ是特殊的子波母函数。DWT可以形式化为一个缩放函数式(2)和一个离散小波函数式(3)。此外,可以通过式(4)和(5)获得x(t)的DWT系数。
| $ \phi(t)_{j, k}=2^{\frac{-j}{2}} \phi\left(2^{-j} t-k\right), $ | (2) |
| $ \varphi(t)_{j, k}=2^{\frac{-j}{2}} \varphi\left(2^{-j} t-k\right), $ | (3) |
| $ a_{\frac{j}{2}}(k)=\int x(t) \phi_{j, k}(t) \mathrm{d} t, $ | (4) |
| $ d_{\frac{j}{2}}(k)=\int x(t) \varphi_{j, k}^{*}(t) \mathrm{d} t, $ | (5) |
其中φ*是φ的复共轭。DWT的系数由近似部分
特别地,每次分解具有对应于低频特征(近似)和高频特征(细节)的两个分支。在DWT的第一级中,原始信号被分解为低频部分“近似分量1”和高频部分“细节分量1”;接下来,将低频部分“近似分量1”连续分解为“近似分量2”和“细节分量2”。经过上述操作三次,将获得多分辨率频域特征:“近似分量”“细节分量1”“细节分量2”和“细节分量3”,以反映行信号在频率上的共同特征。
1.2 卷积神经网络(CNN)由于CNN出色的特征提取能力,它被成功应用于多个领域,例如图像识别、医学成像、故障诊断和时间序列分类[18]。它主要包含卷积和池化操作两个组件。它们通常交替出现在CNN的结构中。卷积运算的过程为
| $ x_{j}^{l}=f\left(x_{l-1} \times k_{j}^{l}\right), j \in J。$ | (6) |
如果使用不同的J滤波器(偏差为b)对第(l-1)个输出xl-1进行卷积,则每个滤波器定义为kjl。卷积运算后,使用激活函数f(·)激活特征图的值。最流行的激活函数是整流线性单元ReLU,它可以增强特征图的非线性特征表达的能力。
池化操作是为了减少特征图的维数,并加速网络的收敛。合并特征具有尺度不变性的属性,这保证了CNN获得鲁棒的特征表示,共有三个池操作,包括最大、最小和平均池。(7)式给出了最大池化操作的示例,
| $ p_{j}^{l+1}=\max \left(x_{j}^{l}(t)\right), j \in J, $ | (7) |
其中:特征映射xjl(t)是从前一个卷积层获得的;t是合并大小。
1.3 长短期记忆神经网络LSTMLSTM可以在门状结构中记住具有长期依赖性的信息,如图 1所示。LSTM的主要组件包括输入门it、遗忘门ft、输出门Ot和当前候选细胞状态
| $ \boldsymbol{f}_{t}=\sigma\left(\boldsymbol{W}_{f} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]+\boldsymbol{b_{f}}\right) ; $ | (8) |
| $ \boldsymbol{i}_{t}=\sigma\left(\boldsymbol{W}_{i} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]+\boldsymbol{b}_{I}\right) ; $ | (9) |
| $ \boldsymbol{O}_{t}=\sigma\left(\boldsymbol{W}_{o} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]+\boldsymbol{b_{o}}\right) ; $ | (10) |
| $ \tilde{\boldsymbol{C}}_{t}=\tanh \left(\boldsymbol{W_{C}} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]+\boldsymbol{b}_{C}\right) 。$ | (11) |
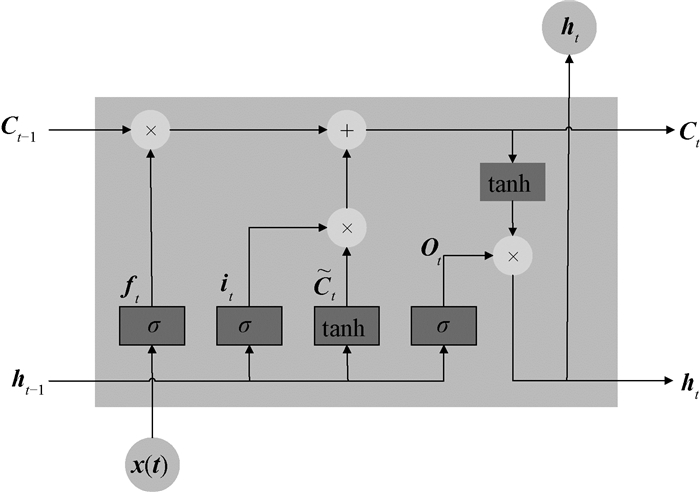
|
图 1 LSTM细胞结构 Fig. 1 LSTM cell structure |
遗忘门和输入门分别决定了当前单元状态Ct中的Ct-1和
| $ \boldsymbol{C}_{t}=\boldsymbol{f}_{t} \cdot \boldsymbol{C}_{t-1}+\boldsymbol{i}_{t} \cdot \tilde{\boldsymbol{C}}_{t} ; $ | (12) |
| $ \boldsymbol{h}_{t}=\boldsymbol{O}_{t} \cdot \tanh \left(\boldsymbol{C}_{t}\right), $ | (13) |
其中:Wf、Wi、Wo分别为遗忘门、输入门、输出门权矩阵;bf、bi和bo分别是遗忘门、输入门和输出门偏置;σ代表sigmoid函数。
2 DWT-CNN-LSTM模型用于超短期光伏发电功率预测的深度模型框架,如图 2所示包括五个步骤:输入,CNN特征提取,LSTM特征提取,特征融合,输出和更新网络。值得注意的是,CNN特征提取包含时域特征提取和频域特征提取。CNN从原始消耗通道和小波分解通道两个通道提取它们。
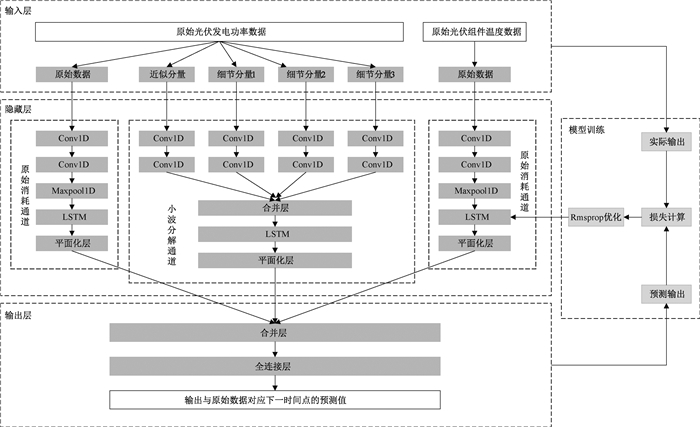
|
图 2 DWT-CNN-LSTM模型 Fig. 2 DWT-CNN-LSTM model |
DWT-CNN-LSTM模型如图 2所示,将原始功率数据进行小波分解,经过实验对比发现小波三级分解优于小波一级分解和小波二级分解,所以使用小波三级分解将光伏功率数据分解为近似分量(approximation)、细节分量1(details1)、细节分量2(details2)和细节分量3(details3)。输入分为三部分:原始功率数据;由小波分解得到的功率数据分量和原始温度数据。
DWT-CNN-LSTM模型预测第i个时间点的功率值,需要前面K个点的功率值和温度值作为输入,称K为序列长度。假设原始功率和温度数据分别为P={p1, p2, …, pn}和T={t1, t2, …, tn},首先把两个样本集划分为训练集Ptrain={p1, p2, …, pm}、Ttrain={t1, t2, …, tm},测试集Ptest={pm+1, pm+2, …,pn}、Ttest={tm+1, tm+2, …, tn},满足m<n, 且m, n∈N。为了加快训练速度以及预测精度,需要对训练集Ptrain和Ttrain中的样本进行归一化处理,根据数据特征,本文选择min-max标准化,所用公式为
| $ \boldsymbol{x}_{i}^{*}=\left(\boldsymbol{x}_{i}-\boldsymbol{x}_{\min }\right) /\left(\boldsymbol{x}_{\max }-\boldsymbol{x}_{\min }\right), $ | (14) |
其中:xi是原始数据;xi*是标准化数据。归一化后的训练集表示为P′train={p′1, p′2, …, p′m}、T′train={t′1, t′2, …, t′m}。将训练集进行样本处理后,就得到了两个(m-K)×K的训练集,rp=Φ′train={φ′1, φ′2, …, φ′m-K}, rt=Ψ′train={ψ′1, ψ′2, …, ψ′m-K},其中:φ′i={p′j-K, p′j-K+1, …, p′j-1};ψ′i={t′j-K, t′j-K+1, …, t′j-1}, 1≤i≤m-K, j=i+K, i, j∈N,一个(m-K)×1训练目标集P′trainY={p′K+1, p′K+2, …, p′m}。原始数据经过预处理之后,样本的时间维度由原来的1维扩张成了K维,解决了原始数据维度过低的问题。测试集通过同样的步骤得到r′p=Φ′test={φ′m+1, φ′m+2, …, φ′n-K},r′t=Ψ′test={ψ′m+1, ψ′m+2, …, ψ′n-K},其中:φ′i={p′j-K, p′j-K+1, …, p′j-1};ψ′i={t′j-K, t′j-K+1, …, t′j-1}, m+1≤i≤n-K, j=i+K, i, j∈ N,P′testY={p′K+m+1, p′K+m+2, …, p′n}。由原始功率训练集Ptrain和测试集Ptest分解的小波分量同样经过上述的数据预处理。
2.2 CNN特征提取将预处理后的数据输入后,使用原始功耗通道和小波分解通道来对超短期光伏功率预测进行建模。原始消耗通道提取时域中的隐藏特征,如图 2中的蓝色虚线框所示,Conv1D的格式为(过滤器个数,过滤器尺寸)。级联了两个一维(1-D)CNN层,以随着增量挖掘不同级别的隐藏特征。两个(1-D) CNN层的详细配置分别是Conv1D(32,5)和Conv1D(64,3)。第一个CNN层用来提取局部特征,而第二个CNN层用于全局特征提取。卷积运算后,使用一个最大池化层(Maxpooling1D),以减小提取特征的尺寸并加快网络速度。从原始消耗通道获得的特征公式为
| $ \left\{\begin{array}{l} \boldsymbol{F}_{\boldsymbol{r}_{p}}= { Maxpooling } 1 D\left({Conv} 1 D_{2}\left(\boldsymbol{r}_{p}^{\prime}\right)\right), \\ \boldsymbol{F}_{\boldsymbol{r}_{t}}= { Maxpooling } 1 D\left({Conv} 1 D_{2}\left(\boldsymbol{r}_{t}^{\prime}\right)\right), \end{array}\right. $ | (15) |
其中: Conv1D2是两个一维卷积层。
DWT通道将获得频域特征,如图 2中红色虚线框所示。DWT转换后的“近似分量”和“细节分量”分别输入一维CNN,以提取频域特征。明显地,多个子细节d1, d2, …, dn包含在“详细信息”部分中。两个(1-D) CNN层分别处理每个组件,格式分别为Conv1D(16,2),Conv1D(32,2)。该过程写为
| $ \left\{\begin{array}{l} F_{a}={Conv} 1 D\left({Conv} 1 D\left(a^{\prime}\right)\right), \\ F_{d_{1}}={Conv} 1 D\left({Conv} 1 D\left(d_{1}^{\prime}\right)\right), \\ F_{d_{2}}={Conv} 1 D\left({Conv} 1 D\left(d_{2}^{\prime}\right)\right), \\ \ \ \vdots \\ F_{d_{n}}={Conv} 1 D\left({Conv} 1 D\left(d_{n}^{\prime}\right)\right), \end{array}\right. $ | (16) |
然后,将来自DWT通道每个分量的一维CNN提取特征进行级联,以获得频域融合特征,公式为
| $ F_{\text {frequency }}= { Concatenate }\left(F_{a}, F_{d_{1}}, F_{d_{2}}, \cdots, F_{d_{n}}\right)。$ | (17) |
尽管之前的操作已经获得了时域和频域特征,但它仍然可能忽略了某些具有长期依赖关系的特征。因此,采用了带有节点为32的LSTM层来提取这种特征。可以用式(18)获得具有长期依赖性的时域和频域特征,其中LSTM()是LSTM操作,
| $ \left\{\begin{array}{l} \boldsymbol{F}_{r_{p}}^{\prime}={LSTM}\left(\boldsymbol{F}_{\boldsymbol{r}_{p}}\right), \\ \boldsymbol{F}_{\boldsymbol{r}_{t}}^{\prime}={LSTM}\left(\boldsymbol{F}_{\boldsymbol{r}_{t}}\right), \\ \boldsymbol{F}_{\text {frequency}}^{\prime}={LSTM}\left(\boldsymbol{F}_{\text {frequency}}\right)。\end{array}\right. $ | (18) |
前面的小节分别从两个通道中提取了具有长期依赖性的时域和频域特征。这个过程是通过使用级联运算来获得具有长期依赖性的时频域融合特征,Flatten()为平面化运算,所用公式为
| $ \begin{aligned} &\boldsymbol{F}_{\text {fusion }}= { Concatenate }\left(F {latten}\left(\boldsymbol{F}_{\boldsymbol{r}_{p}}^{\prime}\right),\right. \\ & { Flatten } \left.\left(\boldsymbol{F}_{\boldsymbol{r}_{t}}^{\prime}\right), { Flatten }\left(\boldsymbol{F}_{\text {frequency}}^{\prime}\right)\right), \end{aligned} $ | (19) |
在模型训练过程中,通过使用梯度算法使预测值与真实值之间的均方误差(MSE)最小化来更新网络。此外,采用优化器RMSProp找到最佳收敛路径,卷积层采用ReLU作为激活函数,全连接层采用sigmoid作为激活函数。使用提出的模型预测下一刻功率的过程公式为
| $ P_{t+1}=D W T-C N N-{LSTM}\left(r_{p}^{\prime}, a^{\prime}, d_{1}^{\prime}, d_{2}^{\prime}, \cdots, d_{n}^{\prime}, r_{t}^{\prime}\right)。$ | (20) |
将原始功率序列r′p、DWT分解分量(a′, d′1, d′2, d′3)和温度序列r′t输入到训练后的DWT-CNN-LSTM模型中,预测下一时刻的功率Pt+1。
3 实验结果 3.1 实验数据实验中使用的数据是2014—2018年从位于浙江省一个光伏发电站收集而来的。数据的测量从早到晚持续大约12 h,测量间隔时间为7.5 min。以2014年10月至2017年2月的数据作为训练集,2017年3月至2018年2月的数据作为测试集。
3.2 评价指标本文采用了平均绝对反正切百分比误差(mean absolute arctan percentage error,MAAPE)、均方根误差(root mean squared error,RMSE)和平均绝对误差(mean absolute error,MAE)三个评价指标对模型的性能进行了评价,它们分别定义为
| $ M A A P E=\left(\sum\limits_{i=1}^{n} \arctan \left(\frac{\left|x_{\text {model }, i}-x_{\text {actual }, i}\right|}{x_{\text {actual }, i}}\right)\right) / n, $ | (21) |
| $ R M S E=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(x_{\text {model }, i}-x_{\text {actual }, i}\right)^{2}}, $ | (22) |
| $ M A E=\frac{1}{n} \sum\limits_{i=1}^{n}\left|x_{\text {model }, i}-x_{\text {actual }, i}\right|, $ | (23) |
其中:xmodel, i为预测值;xactual, i为实际值。
3.3 对比模型文中使用多层感知机(multilayer perceptron,MLP)、支持向量回归(support vector regression,SVR)、CNN和LSTM与本文模型对比。SVR作为机器学习的代表,MLP、CNN、LSTM作为深度学习的代表模型进行对比实验。使用CNN和LSTM与DWT-CNN-LSTM作对比,进一步说明组合模型的性能,以及小波分解对CNN和LSTM的影响。
3.4 预测结果使用Python 3.8.5和Keras 2.3.1版实现了DWT-CNN-LSTM模型。DWT使用了三级分解,CNN使用了两层卷积和一层池化,LSTM层使用32个隐藏单元,而全连接层使用128个隐藏单元。通过随机初始化重建两个DWT-CNN-LSTM模型,重复实验10次,我们将DWT-CNN-LSTM、LSTM、CNN、SVR和MLP模型在春夏秋冬四个季节时间间隔分别为7.5 min、15 min、30 min、60 min的预测结果进行了比较。为了考察DWT-CNN-LSTM模型在不同时刻的预测性能,本文分别在7.5 min、15 min、30 min和60 min的时间间隔进行了实验,预测了一年内的光伏功率。表 1~3列出了五个模型每月和全年的MAAPE、RMSE和MAE三个评价指标值的比较。DWT-CNN-LSTM模型的三个误差度量值大部分低于MLP、CNN、SVR和LSTM模型。说明了DWT通道可以通过提取频域特征进一步提高CNN和LSTM的预测精度。从表中可以看出,相对于其他模型,DWT-CNN-LSTM模型具有最佳性能。
|
|
表 1 不同时间间隔测试数据的MAAPE值 Tab. 1 MAAPE value of test data at different time intervals |
|
|
表 2 不同时间间隔测试数据的RMSE值 Tab. 2 RMSE value of test data at different time intervals |
|
|
表 3 不同时间间隔测试数据的MAE值 Tab. 3 MAE value of test data at different time intervals |
图 3显示了五种预测模型在不同时间范围内的MAE、RMSE和MAAPE柱状图。当时间间隔为7.5 min时,由RMSE和MAE柱状图可以看出,SVR模型的表现优于DWT-CNN-LSTM模型,但从MAAPE柱状图上看,DWT-CNN-LSTM模型的表现优于SVR模型,因此在此时间间隔内,两者预测能力相差不大,而在其他时间间隔DWT-CNN-LSTM模型表现更好。由上述三种柱状图可以看出,当时间间隔为7.5 min时,五种模型都有较好的预测性能,但随着时间间隔的增大,模型预测性能都有明显的下降。根据MAAPE、RMSE和MAE柱状图总体来看,MLP表现最差,显然CNN、SVR、LSTM作为近几年比较流行的单一模型,预测性能要优于MLP,而DWT-CNN-LSTM的各个误差值都明显低于MLP、CNN、SVR和LSTM。总之,与另外四种模型相比,使用MAAPE、RMSE和MAE三种误差指标,DWT-CNN-LSTM具有明显的优势。
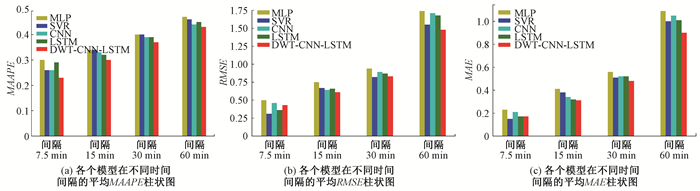
|
图 3 不同预测评价指标的比较 Fig. 3 Comparison of different predictive evaluation indicators |
为了验证本文提出的DWT-CNN-LSTM模型的性能,从网上找到了14个月光伏发电功率的公开数据集进行验证,数据包括2018年1月到2019年4月,从中取2018年1月到2019年2月作为训练集,2019年3月到2019年4月作为测试集,进行模型训练和预测。由于时间间隔为7.5 min的预测结果各个模型相差不大,因此只进行时间间隔为15 min、30 min和60 min的实验。
实验结果依然使用MAAPE、RMSE和MAE三个评价指标进行评估,结果如表 4~6所示。本文提出的DWT-CNN-LSTM方法在MAAPE指标上和其他方法相比较,比MLP、CNN、LSTM分别提升了8.82%、3.13%、6.06%。在RMSE指标上和其他方法相比较,比MLP、SVR、CNN、LSTM分别提升了9.40%、7.02%、7.02%、5.36%。在MAE指标上和其他方法相比较,比MLP、SVR、CNN、LSTM分别提升了12.68%、7.46%、7.46%、4.62%。因此经过实验验证,DWT-CNN-LSTM模型相对于其他模型有较好的预测性能。
|
|
表 4 两个月不同时间间隔的MAAPE的比较 Tab. 4 Comparison of MAAPE at different time intervals of two months |
|
|
表 5 两个月不同时间间隔的RMSE的比较 Tab. 5 Comparison of RMSE at different time intervals of two months |
|
|
表 6 两个月不同时间间隔的MAE的比较 Tab. 6 Comparison of MAE at different time intervals of two months |
光伏发电功率预测对于维护电网安全、协调资源利用具有重要意义。本文提出了一种基于离散小波变换(DWT)、卷积神经网络(CNN)和长短期记忆神经网络(LSTM)的新型域融合深度模型。与传统的预测模型不同,DWT-CNN-LSTM模型除了利用CNN提取时域特征之外,还利用CNN通过DWT通道提取频域特征,再利用LSTM学习长期依赖信息,增强了CNN和LSTM模型的预测能力。
实验中,我们使用了一个真实的数据集。通过比较研究,得出了在四个季节不同时间间隔中MLP、SVR、CNN、LSTM和DWT-CNN-LSTM模型的三个不同的误差指标。结果表明,与其他方法相比,DWT-CNN-LSTM具有明显的优势。
本研究的未来工作包括将DWT-CNN-LSTM模型应用到风力发电预测中,针对不同的领域,进一步检验此模型算法的性能。
| [1] |
WANG H Z, YI H Y, PENG J C, et al. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network[J]. Energy conversion and management, 2017, 153: 409-422. DOI:10.1016/j.enconman.2017.10.008 (  0) 0) |
| [2] |
LI, WANG, ZHANG, et al. Recurrent neural networks based photovoltaic power forecasting approach[J]. Energies, 2019, 12(13): 2538. DOI:10.3390/en12132538 (  0) 0) |
| [3] |
ANTONANZAS J, OSORIO N, ESCOBAR R, et al. Review of photovoltaic power forecasting[J]. Solar energy, 2016, 136: 78-111. DOI:10.1016/j.solener.2016.06.069 (  0) 0) |
| [4] |
WANG H Z, LEI Z X, ZHANG X, et al. A review of deep learning for renewable energy forecasting[J]. Energy conversion and management, 2019, 198: 111799. DOI:10.1016/j.enconman.2019.111799 (  0) 0) |
| [5] |
ALONSO-MONTESINOS J, BATLLES F J. Solar radiation forecasting in the short- and medium-term under all sky conditions[J]. Energy, 2015, 83: 387-393. DOI:10.1016/j.energy.2015.02.036 (  0) 0) |
| [6] |
WANG H Z, LI G Q, WANG G B, et al. Deep learning based ensemble approach for probabilistic wind power forecasting[J]. Applied energy, 2017, 188: 56-70. DOI:10.1016/j.apenergy.2016.11.111 (  0) 0) |
| [7] |
YANG T G, LI B, XUN Q. LSTM-attention-embedding model-based day-ahead prediction of photovoltaic power output using Bayesian optimization[J]. IEEE access, 2019, 7: 171471-171484. DOI:10.1109/ACCESS.2019.2954290 (  0) 0) |
| [8] |
WANG H Z, WANG G B, LI G Q, et al. Deep belief network based deterministic and probabilistic wind speed forecasting approach[J]. Applied energy, 2016, 182: 80-93. DOI:10.1016/j.apenergy.2016.08.108 (  0) 0) |
| [9] |
蒋建东, 余沣, 董存, 等. 基于PSO与ELM组合算法的短期光伏发电功率预测模型[J]. 郑州大学学报(理学版), 2019, 51(3): 120-126. JIANG J D, YU F, DONG C, et al. A short-term photovoltaic power forecasting model based on PSO and ELM combined algorithm[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(3): 120-126. (  0) 0) |
| [10] |
徐华, 刘红琳. 一种基于神经网络的时序建模预测方法[J]. 郑州大学学报(自然科学版), 1998, 30(2): 23-26, 39. XU H, LIU H L. A time series prediction and system modeling method based neural network[J]. Journal of zhengzhuou university (natural science edition), 1998, 30(2): 23-26, 39. (  0) 0) |
| [11] |
SRIVASTAVA S, LESSMANN S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data[J]. Solar energy, 2018, 162: 232-247. DOI:10.1016/j.solener.2018.01.005 (  0) 0) |
| [12] |
HUANG C J, KUO P H. Multiple-input deep convolutional neural network model for short-term photovoltaic power forecasting[J]. IEEE access, 2019, 7: 74822-74834. DOI:10.1109/ACCESS.2019.2921238 (  0) 0) |
| [13] |
LIU J, FANG W L, ZHANG X D, et al. An improved photovoltaic power forecasting model with the assistance of aerosol index data[J]. IEEE transactions on sustainable energy, 2015, 6(2): 434-442. DOI:10.1109/TSTE.2014.2381224 (  0) 0) |
| [14] |
CHEN C S, DUAN S X, CAI T, et al. Online 24-h solar power forecasting based on weather type classification using artificial neural network[J]. Solar energy, 2011, 85(11): 2856-2870. DOI:10.1016/j.solener.2011.08.027 (  0) 0) |
| [15] |
MELLIT A, MASSI PAVAN A, LUGHI V. Short-term forecasting of power production in a large-scale photovoltaic plant[J]. Solar energy, 2014, 105: 401-413. DOI:10.1016/j.solener.2014.03.018 (  0) 0) |
| [16] |
ABDEL-NASSER M, MAHMOUD K. Accurate photovoltaic power forecasting models using deep LSTM-RNN[J]. Neural computing and applications, 2019, 31(7): 2727-2740. DOI:10.1007/s00521-017-3225-z (  0) 0) |
| [17] |
李畸勇, 班斓. 基于长短记忆神经网络的短期光伏发电预测技术研究[J]. 华北电力大学学报(自然科学版), 2020, 47(4): 46-52. LI J Y, BAN L. Research on short-term photovoltaic power forecasting technology based on LSTM[J]. Journal of North China electric power university (natural science edition), 2020, 47(4): 46-52. DOI:10.3969/j.ISSN.1007-2691.2020.04.06 (  0) 0) |
| [18] |
SHAO X R, SOO KIM C, GEUN KIM D. Accurate multi-scale feature fusion CNN for time series classification in smart factory[J]. Computers, materials & continua, 2020, 65(1): 543-561. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


