2. 北方工业大学 大规模流数据集成与分析实验室 北京 100144
2. Beijing Key Laboratory on Integration and Analysis of Large-Scale Stream Data, North China University of Technology, Beijing 100144, China
工作流普遍应用于大规模科学问题和工业控制问题的建模领域中,通常被建模为通过数据或计算依赖相互连接的一组任务。云计算环境作为最新兴的分布式计算环境,为工作流的调度与执行带来了更有效的平台与技术支撑[1]。云以虚拟机的形式提供计算资源,而工作流中任务与计算资源间的映射问题即为工作流调度问题[2]。
过去工作中所提出的任务调度算法,根据调度目标的数量,可以分为针对单一目标优化的传统任务调度和针对多目标优化的启发式思想的智能化算法[3]。单目标优化的任务调度算法[4]重点在于单一目标的最优解,通常会局限于某个目标最优,而无法考虑到全局,导致这些研究的应用场景十分有限。
当需要同时考虑用户提出的多个服务质量(quality of service,QoS)目标时,可以通过智能化算法进行求解[5-6]。在目前所提出的相关工作中,主要是根据工作流以及云环境参数等,将工作流在云上的调度问题建模为多目标优化问题,然后采用基于生物启发或基于群体智能的算法计算结果,如粒子群算法(particle swarm optimization,PSO)[7],第二代非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)等。
然而对于需要周期性提交的数据处理类工作流而言,不同时段任务负载的变化可能会改变已经建模的多目标优化问题的一些环境参数。而静态的多目标优化算法,在迭代选择过程中具有一定的趋同性,可能导致在新环境下种群多样性的缺失,最终无法在新环境下得出多样性较好的非支配解集。如果重启算法,算法重新收敛的过程则可能无法满足实时性要求。因此,将此类工作流调度问题作为动态多目标优化问题进行建模求解更为合适,并且在算法中还需要对环境变化做出及时响应和调整。
目前对于动态多目标优化问题所提出的环境变化响应策略主要可以分为四类: 多样性保持;记忆策略;迁移学习;预测机制[8]。多样性保持通过维持或提高种群的多样性,提升动态多目标优化求解问题的能力[9]。但是,对于变化形式复杂或变化程度较强的动态多目标优化问题,该方式可能会导致较差的问题追踪性能。记忆策略通常适用于解决具有周期变化特性的动态多目标优化问题,通过隐式或显式地找到存储在过去环境中的解,当环境发生变化时,重用存储的解的历史信息实现对当前环境下最优解的快速跟踪[10-11]。然而,此类方法适用范围有限,当环境变化多样性较高时,这类方法需要存储大量的数据,不仅消耗大量的存储资源,在重用这些历史信息时,算法的效率也会降低。迁移学习充分利用具有相似特性的问题信息,指导当前问题的预测或分类,为动态多目标优化问题提供了新的解决思路,但是,在动态多目标优化问题求解上的应用还处于起步阶段。预测模型的方法是近年来的研究热点,主要是采用预测的方法,从过去的环境中提取信息,然后预测新环境下的解[12-13]。此类方法比多样性保持和记忆策略具有更广泛的适用性,但是该方法的有效性依赖于数据集的质量以及模型的选择和训练。若预测误差较大则会影响对寻优过程的准确引导。
在本文中,将数据处理类工作流的调度问题建模为动态多目标优化问题,其中动态变化来源于任务的数据负载量变化。我们采用预测模型的方式作为环境变化响应策略,结合序列到序列模型(sequence to sequence model, Seq2Seq),提出了动态第二代非支配排序结合Seq2Seq模型遗传算法(dynamic non-dominated sorting genetic algorithm-Ⅱ-Seq2Seq,DNSGA-Ⅱ-Seq2Seq)。
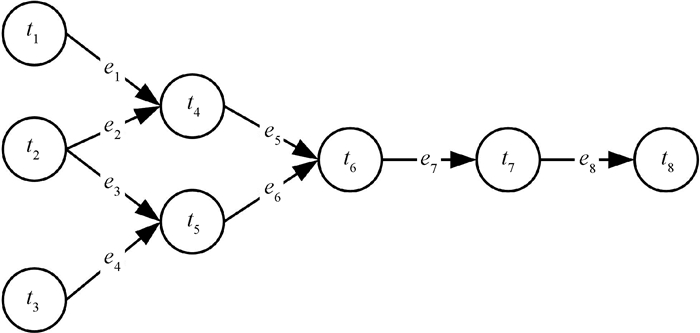
1 动态工作流调度问题建模 1.1 工作流应用建模工作流应用通常被建模为一个有向无环图W=(T, E),其中:T=(t1, t2, …, tn)代表任务集合;E=(e1, e2, …, em)代表有向边集合。如图 1所示。
|
图 1 工作流应用建模图 Fig. 1 Workflow application modeling diagram |
对于需要周期性调度的数据处理类工作流而言,数据源产生数据的速率会发生变化,因此工作流中单个任务单位时间需要处理的数据量也会发生变化。对此,我们进一步将编号为i的任务建模为ti=(MIi, λi, γi),其中:MIi表示处理一个单位数据需要的工作量;λi表示接入的数据流速率;γi表示该服务产生的数据流速率。
我们对云、边、端的混合环境进行了简化,只是在设置带宽和计算能力的时候,将区别出云中的主机和边缘服务器上的主机。我们将其建模为多个集群的拓扑连接Q=(C, B, D), 其中:C=(c1, c2, …, cn)代表集群;B、D分别是带宽矩阵和数据传输代价矩阵。对于单个编号为g的集群中心cg,有cg=(vm1g, vm2g, …, vmkg, Ug), 其中:vmkg表示编号为k的具体虚拟机;Ug表示集群中的各虚拟机内部的带宽。对于单台虚拟机vmkg,有vmkg=(MIPSvmkg, costvmkg), 其中:MIPSvmkg代表计算能力;costvmkg代表单位计算代价。
1.2 优化目标在本文中,我们所考虑的需要优化的QoS目标是总成本、最大完工时间和任务分配不平衡度,下面对这三个目标进行介绍。
1.2.1 总成本总成本也称总代价,本文中由计算代价和传输代价两部分组成,当任务实例运行开始后,接入该任务的数据需要传输代价,处理数据过程需要计算代价。总代价计算公式为
| $ {cost}(W)=\sum\limits_{t_i \in T}\left( {transfer}\left(t_i\right)+ {exec}\left(t_i\right)\right), $ | (1) |
其中:transfer(ti)代表单个任务ti的传输代价;exec(ti)代表单个任务的计算代价。
计算代价的计算方式是根据部署的虚拟机每秒运算的浮点数转化为需要执行的时间,再根据执行时间加上单位时间所需的计算代价转化为单个任务的计算代价。单个任务ti的计算代价的计算公式为
| $ {exec}\left(t_i\right)= {cost}_{v m_k^g} * {in}\left(t_i\right) * M I_{t_i} / M I P S_{v m_k^g}, $ | (2) |
其中:costvmkg表示该任务所部署的虚拟机的单位计算代价;MIPSvmkg代表该任务所部署的虚拟机计算能力;MIti表示该任务处理一个单位数据需要的工作量;in(ti)表示输入该任务的数据量。
传输代价指的是由所有的父亲节点传输到该任务中的数据传输代价之和,单个任务ti的传输代价的计算公式为
| $ {transfer}\left(t_i\right)=\sum\limits_{t_j \in { parent }\left(t_i\right)} c\left(t_j\right), $ | (3) |
| $ c\left(t_i\right)=\left\{\begin{array}{l} 0, \quad \text { if } t_i \text { 与 } t_j \text { 在相同虚拟机上, } \\ { out }\left(t_j\right) * \boldsymbol{D}\left(C_g\left(t_j\right), C_g\left(t_i\right)\right), \quad \text { 其他。} \end{array}\right. $ | (4) |
其中:parent(ti)表示任务ti的所有父节点;out(tj)表示父节点tj传输给ti的数据量;D(Cg(tj), Cg(ti))表示带宽矩阵中对应tj和ti的值。
1.2.2 系统最大完成时间系统最大完成时间指的是工作流中所有任务都完成的时间。工作流中任务的执行必须满足其定义的数据依赖关系,所以每个任务执行必须等待其所有前驱任务执行完毕。因此,对于单个任务ti,有公式(5)和(6):
| $ T_{t_i}^{\text {Begin }} \geqslant \max \limits_{t_j \in { parent }\left(t_i\right)}\left\{T_{t_j}^{\text {End }}+T_{t_j}^{\text {Trans }}\left(C_g\left(t_j\right), C_g\left(t_i\right)\right)\right\} ; $ | (5) |
| $ T_{t_i}^{\text {End }}=T_{t_i}^{\text {Begin }}+T_{ {exec }}\left(t_i, v m_k^g\right) 。$ | (6) |
综上可得,系统最大完成时间TWFinal的计算公式为
| $ T_W^{\text {Final }}=\max \limits_{t_i \in T}\left\{T_{t_i}^{\text {End }}\right\}。$ | (7) |
其中:TtiBegin表示任务ti的开始时间;TtjEnd代表任务ti的一个父节点tj的结束时间;TtjTrans(Cg(tj),Cg(ti))代表数据传输时间;TtiEnd表示任务ti的结束时间;Texec(ti, vmkg)代表任务ti在vmkg虚拟机上的计算时间。
1.2.3 任务分配不平衡度任务分配的不平衡度主要计算分配到不同集群中心上任务个数的差异,计算方式为
| $ { Unbalance }=\left(N_{\max }-N_{\min }\right) / N_{\text {avg }} , $ | (8) |
其中:Nmax代表被分配任务最多的数据中心的任务个数;Nmin代表被分配任务最少的数据中心的任务个数;Navg代表分配任务个数的均值。
2 工作流动态调度多目标进化算法 2.1 NSGA-Ⅱ算法NSGA-Ⅱ算法是求解静态的多目标优化问题的常用算法,它通过基于非支配排序的方法保留了种群中的优良个体,提出了快速非支配排序算法,引入精英策略、拥挤度和拥挤度比较算子,降低算法时间复杂度的同时保证种群多样性。
然而,用于解决静态多目标优化问题的NSGA-Ⅱ算法在出现环境参数变化时,可能会出现种群多样性缺失问题,从而无法在新环境下得到多样性较好的非支配解集。对此,我们对NSGA-Ⅱ算法进行了改进,提出了DNSGA-Ⅱ-Seq2Seq算法,下面进行介绍。
2.2 DNSGA-Ⅱ-Seq2Seq算法我们采用了基于预测模型的方法来解决NSGA-Ⅱ算法在动态变化环境下可能出现的种群多样性缺失问题。主要有两方面考虑,首先是算法的收敛速度,随机初始化种群中的部分或全部个体可能会导致算法收敛速度降低; 其次是算法使用的存储资源,对于数据负载的连续变化,若采用记忆策略的算法,则可能需要存储大量的数据,不仅耗费的存储资源较多,且重用速率也会相应降低。
Seq2Seq模型是目前自然语言处理技术中使用较多的一个模型,常用于将一个语言序列翻译成另一种语言序列。它由编码器(encoder)和解码器(decoder)两部分组成,其中encoder和decoder可以由卷积神经网络(convolutional neural network,CNN)、循环神经网络(recurrent neural network,RNN)、Transformer模型三种结构中的任意一种组合。我们将调度方案看作虚拟机编号的序列,然后采用Seq2Seq模型来学习局部最优解的变化规律,算法伪代码如算法1所示。
算法1 DNSGA-Ⅱ-Seq2Seq算法
输入:构建好的训练集T。
输出:非支配解集Pareto,即最优调度方案。
1) 通过T训练Seq2Seq模型;
2) 随机初始化种群;
3) WHILE未达到终止条件DO
4) IF环境发生变化THEN
5) 通过模型预测新环境下的解Solution;
6) 将Solution添加到种群中;
7) END IF
8) 种群个体非支配排序和拥挤度计算;
9) 挑选种群中非支配个体;
10) 产生子代;
11) END WHILE;
12) 产生非支配解集Pareto。
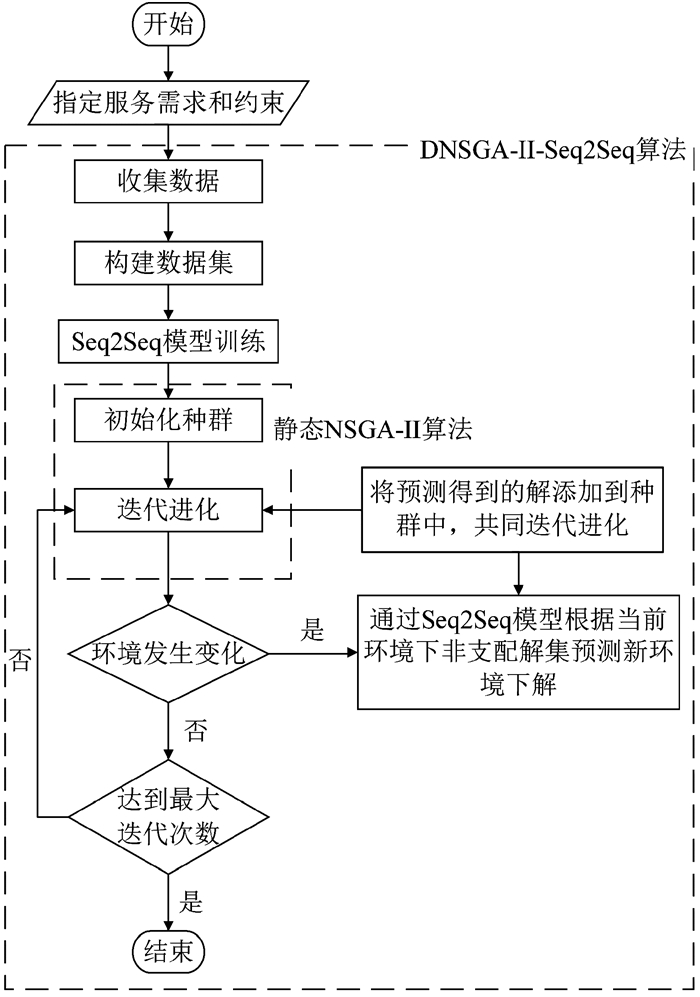
将DNSGA-Ⅱ-Seq2Seq算法用于动态工作流调度问题的算法流程如图 2所示,在提交工作流应用并指定需要优化的目标和约束之后,首先收集历史连续环境下的局部最优解(即非支配解集),然后根据环境的连续性以及解的对应关系构建数据集,基于该数据集训练Seq2Seq模型。在静态的NSGA-Ⅱ算法的种群迭代过程中,如果发生了环境变化,则可以通过Seq2Seq模型,根据当前环境下的局部最优解预测新环境下的能较好适应环境的解,将这些解加入种群中共同进化,可解决种群多样性缺失的问题。达到最大迭代次数后,可以得到多样性和收敛性都较好的解,将这些解作为调度方案来部署工作流任务,分配虚拟机资源。
|
图 2 DNSGA-Ⅱ-Seq2Seq算法流程图 Fig. 2 Flow chart of DNSGA-Ⅱ-Seq2Seq algorithm |
由NSGA-Ⅱ算法得到的非支配解集可以很好地表示从每个子区域中找到的局部最优解。但NGSA-Ⅱ算法中种群的随机初始化和种群迭代选择过程给算法带来了一些随机性,因此如果在某种环境下只做一次NSGA-Ⅱ算法,得到的非支配解集的准确性和多样性较差,从而带来一些噪声,影响模型的训练和预测精度。针对此问题,可以对同一环境重复a次NSGA-Ⅱ算法,得到a个不同的非支配解集,然后对这些非支配解集进行合并去重,再进行快速非支配排序,最终只取合并后的解集中的非支配解。这样处理后的解集在多样性和准确性上将会优于单次实验所得出的非支配解集。每个环境下最终获取的非支配解集称为存档R。
2.2.2 数据集构建通过上一步收集的每一种环境下的存档R1, R2, …, Ra构建训练集来学习局部最优解的变化规律。为了达到这一点,数据集中必须包含局部最优解在连续不同环境下的变化信息。由于环境参数的变化往往是连续的,所以对于同一局部子区域,环境变化前后的局部最优解可能非常接近。因此,我们将连续两个环境下的邻近局部最优解考虑为同一局部子区域,将其进行配对,即可表示在环境变化时局部最优解的变化规律。
因此可以通过计算决策空间的欧氏距离来找寻解的对应关系,计算方法为
| $E L(\boldsymbol{p}, \boldsymbol{q})=\sqrt{\sum\limits_{l=1}^L\left(p_l-q_l\right)^2}, $ | (9) |
其中:p、q分别代表来自两个相邻环境的存档Rd-1和Rd的解;L代表决策空间的维数。通过不断找出距离最近的非支配解对,可以得到能反映环境变化信息的训练集数据Train={(p1, q1), (p2, q2), …, (pv, qv)}。需要说明的有两点:第一每个非支配解只能配对一次;第二是上一环境存档的解和下一环境存档的解的数量可能不相同。在这种情况下,只取欧氏距离最近的非支配解对,直至某一个环境的所有解都匹配完成。若保存的非支配解对不是距离最近的,可能无法表示同一区域的非支配解的变化规律,从而影响数据集质量。
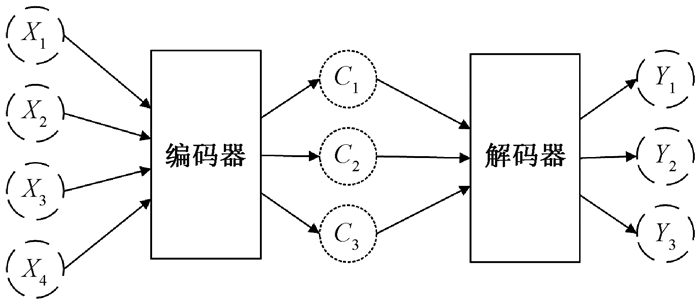
2.2.3 基于历史数据训练Seq2Seq模型在基于历史数据完成数据集的构建之后,我们采用Seq2Seq模型来学习局部最优解的变化规律,模型的结构如图 3所示。
|
图 3 Seq2Seq模型结构图 Fig. 3 Seq2Seq model structure diagram |
在本文中,Seq2Seq模型的编码器和解码器均采用RNN来实现,每层的神经元个数为128。首先,编码器的输入为上一环境的局部最优解,即所构建的非支配解集对中的样例数据,通过RNN输出最后一个时刻μ的隐藏状态信息(hμ, cμ)作为语义向量M。然后解码器将M作为初始状态输入RNN中,根据语义向量生成新的隐藏状态向量(h′θ, c′θ),θ∈(0, μ)。最后由一个线性层将解码器输出的隐藏状态信息转换成最终的输出序列。
在该模型中,由于输出层采用Softmax激活函数,所以得到的是序列中每个位置上不同分类的概率分布,因此我们采用CrossEntropyLoss作为损失函数,即交叉熵,它主要刻画的是实际输出的概率分布与期望输出的概率分布的距离,假设概率分布β为期望输出,概率分布ρ为实际输出,则交叉熵计算方法为
| $ \begin{aligned} & H(\boldsymbol{\beta}, \boldsymbol{\rho})=-\sum\limits_x(\boldsymbol{\beta}(x) \log \boldsymbol{\rho}(x)+ \\ & (1-\boldsymbol{\beta}(x)) \log (1-\boldsymbol{\rho}(x)))。\end{aligned} $ | (10) |
本文中所采用的优化器为Adam优化器。模型构建完成后,将上述所获得的数据集输入,进行模型的训练,当损失函数所计算的值收敛到较低的值时,认为该模型已训练完成。
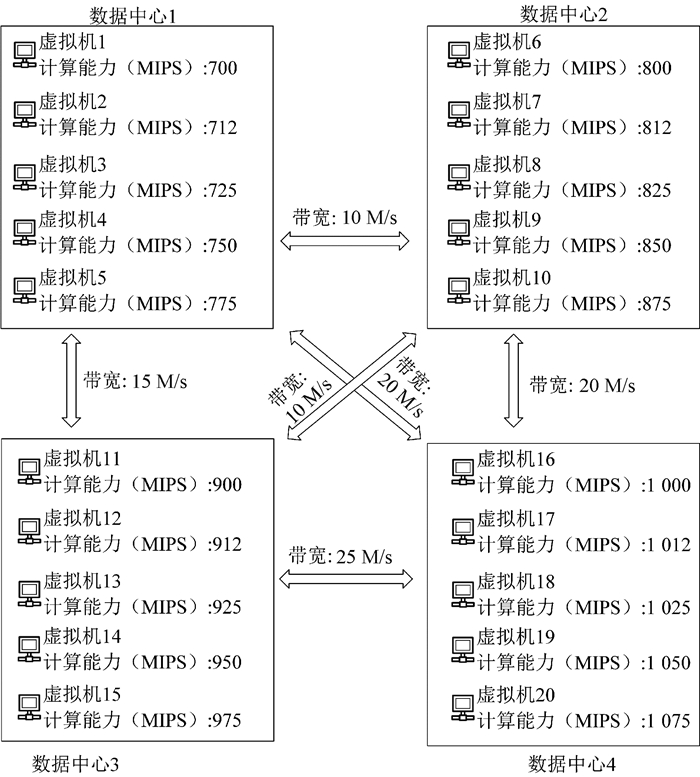
3 实验 3.1 实验设置本文的实验是基于改进后的WorkflowSim仿真平台完成的。在集群中心和虚拟机配置上,设置了四个不同的数据中心。每个数据中心包括了五个主机,每个虚拟机计算能力均不相同,数据中心之间的带宽也不相同,具体的拓扑图如图 4所示。
|
图 4 数据中心和虚拟机配置拓扑图 Fig. 4 Data center and virtual machine configuration topography |
本文实验所采用的工作流为常见的科学工作流中的Montage工作流,常用于天文图像数据分析处理,本实验中采用的任务数为20个。
为了体现数据负载的变化,我们设置了φ值,将该值乘以工作流任务所设置的数据负载量,得出实际参与计算的数据负载量,以此模拟工作流中的任务的数据负载量变化。
3.2 对比算法为了验证我们所提出的DNSGA-Ⅱ-Seq2Seq算法的有效性,选取了另外两种动态多目标优化算法,包括DNSGA-Ⅱ-A算法和NN-DNSGA-Ⅱ算法。
DNSGA-Ⅱ-A算法是基于多样性的环境响应策略的方法,当环境发生变化时,随机初始化种群中的一些个体,以此引入多样性。该算法原理简单并易于实现,但是不恰当的替代比例可能导致种群丧失有效信息,甚至误导后续进化过程。同时,算法的随机性也可能带来性能和结果上的波动。本实验设置的随机初始化比例为0.3。
NN-DNSGA-Ⅱ算法基于预测模型的方法来改进NSGA-Ⅱ算法,采用的是简单的全连接网络。该算法一方面没有通过上述提到的多次实验并聚合处理的方式提高数据集质量,另一方面简单的全连接网络并不能很好地学习到局部最优解的变化规律。在本实验中,全连接网络设置为三层结构,包括一个输入层、一个隐藏层和一个输出层。输入层和输出层的神经元数量等于工作流中的任务数量,隐藏层中的神经元数量等于任务数量的两倍。
3.3 评价指标我们将从两个方面来说明DNSGA-Ⅱ-Seq2Seq算法的有效性。一是产生的新个体的好坏,另一方面则是评价加入这些个体后的NSGA-Ⅱ算法在新环境下收敛得出的非支配解集的好坏。评价新个体的好坏,采用的是超体积(hypervolume,HV)指标。该指标可以测量在非支配解相对于参考点所覆盖的空间量,计算公式为
| $H V(P O F)=\delta * \cup _{\boldsymbol{I} \in P O F} V\left(\boldsymbol{I}, \boldsymbol{I}^*\right), $ | (11) |
其中:O代表目标空间;I代表单个非支配解;POF代表非支配解集;δ代表勒森伯格测度;V(I,I*)表示参照点I*与非支配解I构成超立方体体积。
HV指标越大,则说明相对于参考点,非支配解集分布得越好,解的多样性越高。我们先将所有目标函数的值进行标准化,然后以(1, 1, 1)点为参考点计算HV指标。我们采用三个指标来确定算法得出非支配解集的好坏:第一个是上述提到的HV指标;第二个是非支配解集在目标空间上各维度的最低值,该指标可以很直观地评价结果的优劣;第三个是斯科特间距(Schott′s spacing,Spacing),该指标主要度量每个解到其他解的最小距离的标准差,该指标越小,说明解集分布越均匀,计算公式为
| $ {Spacing}(P O F)=\sqrt{\frac{1}{|P O F|-1} \sum\limits_{i=1}^{|P O F|}\left(\boldsymbol{S}_I-\overline{\boldsymbol{S}}\right)^2} \text {, } $ | (12) |
其中:POF表示非支配解集;|POF|代表非支配解的个数;SI表示非支配解I与最邻近非支配解的欧氏距离;SI代表所有SI的均值。
3.4 实验结果为了评价加入种群的个体的好坏,我们进行了多次连续实验,实验结果如表 1所示,最左列T代表连续实验的次数,表格中的数值为多次连续实验HV指标的均值,表中加黑数值表示在三种算法横向对比中HV值最大,效果最好。可以看出,在相同的条件下,DNSGA-Ⅱ-Seq2Seq算法产生的个体在新环境下HV指标均优于其他算法,个体的多样性更好,更有利于增加种群的多样性,从而更好地解决算法在动态环境下种群多样性缺失的问题。
|
|
表 1 评价个体实验结果 Tab. 1 Evaluation of individual experimental results |
同样,我们也做了多次连续实验来评价DNSGA-Ⅱ-Seq2Seq算法,如表 2和表 3所示,其中负载φ值代表的工作流负载的增大倍数。表 2展示的是这三种算法在新环境下收敛后非支配解集在目标空间上各个维度上的最小值,Unbalance代表的是不平衡度,Time代表的是最大完成时间,Cost代表总成本。表 3展示的是这三种算法得到的非支配解集的HV指标和Spacing指标,表中的加黑数值表示在三种算法横向对比中该算法效果最好。
|
|
表 2 评价非支配解集实验结果1 Tab. 2 Evaluation of non-dominated set experimental results 1 |
|
|
表 3 评价非支配解集实验结果2 Tab. 3 Evaluation of non-dominated set experimental results 2 |
根据实验结果可以看出,尽管NSGA-Ⅱ算法的种群随机初始化过程为最终的结果带来了一些随机性,DNSGA-Ⅱ-Seq2Seq算法的最终结果无论从目标函数值还是从HV指标和Spacing指标来看,在大多数情况下均优于其他两种经典算法,证明了DNSGA-Ⅱ-Seq2Seq算法在解决动态多目标优化问题上的有效性。
4 结论本文针对需要周期性提交的数据处理类工作流在云环境上的调度问题,提出了DNSGA-Ⅱ-Seq2Seq算法,考虑到此类数据工作流在不同时段进行调度时任务的工作负载动态变化特性,将该问题建模为动态多目标优化问题,优化目标包括不平衡度、总成本和最大完成时间。为了解决NSGA-Ⅱ算法在面对环境变化时存在的种群多样性缺失问题,通过Seq2Seq模型学习历史环境下局部最优解的变化规律,在环境变化时根据当前环境下的非支配解预测新环境下的解,帮助NSGA-Ⅱ算法在新环境下增加种群多样性并快速收敛。在改进后的WorkflowSim仿真平台进行了仿真实验,验证了DNSGA-Ⅱ-Seq2Seq算法的有效性。
| [1] |
田倬璟, 黄震春, 张益农. 云计算环境任务调度方法研究综述[J]. 计算机工程与应用, 2021, 57(2): 1-11. TIAN Z J, HUANG Z C, ZHANG Y N. Review of task scheduling methods in cloud computing environment[J]. Computer engineering and applications, 2021, 57(2): 1-11. (  0) 0) |
| [2] |
姜春茂, 王凯旋. 基于三支队列的实时云任务节能调度算法[J]. 郑州大学学报(理学版), 2019, 51(2): 66-71. JIANG C M, WANG K X. Real-time cloud tasks schedule algorithm for saving energy based on tri-queue system[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(2): 66-71. (  0) 0) |
| [3] |
杨戈, 赵鑫, 黄静. 面向云计算的任务调度算法综述[J]. 计算机系统应用, 2020, 29(3): 11-19. YANG G, ZHAO X, HUANG J. Survey on task scheduling algorithms for cloud computing[J]. Computer systems & applications, 2020, 29(3): 11-19. (  0) 0) |
| [4] |
RODRIGUEZ M A, BUYYA R. Deadline based resource provisioningand scheduling algorithm for scientific workflows on clouds[J]. IEEE transactions on cloud computing, 2014, 2(2): 222-235. DOI:10.1109/TCC.2014.2314655 (  0) 0) |
| [5] |
GARG R, SINGH A K. Multi-objective workflow grid scheduling using ε-fuzzy dominance sort based discrete particle swarm optimization[J]. The journal of supercomputing, 2014, 68(2): 709-732. DOI:10.1007/s11227-013-1059-8 (  0) 0) |
| [6] |
GARG R, SINGH A K. Multi-objective workflow grid scheduling based on discrete particle swarm optimization[C]//Swarm, Evolutionary, and Memetic Computing. Berlin: Springer, 2011: 183-190.
(  0) 0) |
| [7] |
何留杰, 李波. 满足帕累托最优的多目标云工作流调度算法[J]. 计算机应用与软件, 2019, 36(5): 289-297. HE L J, LI B. Multi-objective cloud workflow scheduling algorithm satisfying Pareto optimality[J]. Computer applications and software, 2019, 36(5): 289-297. (  0) 0) |
| [8] |
肖晓伟, 肖迪, 林锦国, 等. 多目标优化问题的研究概述[J]. 计算机应用研究, 2011, 28(3): 805-808. XIAO X W, XIAO D, LIN J G, et al. Overview on multi-objective optimization problem research[J]. Application research of computers, 2011, 28(3): 805-808. DOI:10.3969/j.issn.1001-3695.2011.03.002 (  0) 0) |
| [9] |
SAHMOUD S, TOPCUOGLU H R. Sensor-based change detection schemes for dynamic multi-objective optimization problems[C]//2016 IEEE Symposium Series on Computational Intelligence. Athens: IEEE Press, 2016: 1-8.
(  0) 0) |
| [10] |
YANG S X, YAO X. Population-based incremental learning with associative memory for dynamic environments[J]. IEEE transactions on evolutionary computation, 2008, 12(5): 542-561. (  0) 0) |
| [11] |
SAHMOUD S, TOPCUOGLU H R. A memory-based NSGA-Ⅱ algorithm for dynamic multi-objective optimization problems[C]//European Conference on the Applications of Evolutionary Computation. Porto: Springer International Publishing, 2016: 296-310.
(  0) 0) |
| [12] |
丁进良, 杨翠娥, 陈立鹏, 等. 基于参考点预测的动态多目标优化算法[J]. 自动化学报, 2017, 43(2): 313-320. DING J L, YANG C E, CHEN L P, et al. Dynamic multi-objective optimization algorithm based on reference point prediction[J]. Acta automatica sinica, 2017, 43(2): 313-320. (  0) 0) |
| [13] |
LIU X F, ZHAN Z H, ZHANG J. Neural network for change direction prediction in dynamic optimization[J]. IEEE access, 2018, 6: 72649-72662. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


