0 引言

子空间聚类假定数据点来自多个潜在低维子空间，然后对处于多个潜在低维子空间上的高维数据点进行聚类。子空间聚类方法得到了很好的发展，涌现出许多子空间聚类模型来揭示数据分布的这些低维子空间，以便可以正确分割数据中的所有簇，并且每个簇都在一个低维子空间。近年来已经开发了许多子空间聚类方法，例如基于迭代的方法^[1-2]、基于因子分解的方法^[3-4]、统计方法^[5]以及基于谱聚类的方法^[6-7]。文献[8]提出低秩子空间分割以找到具有低秩表示的子空间结构。文献[9]提出稀疏子空间聚类以找到与来自相同子空间的数据点相对应的稀疏表示，在获得子空间表示后，可以对这种新的表示执行谱聚类。目前，以谱聚类^[10]为基础的子空间聚类方法受到广泛关注。谱聚类是一种以图论为基础的聚类方法, 它将数据集中的每个数据当作图的顶点, 数据之间的相似度当作带权的边, 这样就转化为对图的划分来解决数据聚类^[11]。基于谱聚类的子空间聚类方法，其基本过程为:通过找出样本在低维子空间的表示系数来构造相似度矩阵, 然后利用谱聚类方法获得数据的聚类结果。上述方法主要关注单一数据来源的特征，而不是多个数据来源的特征。本文将对具有多视图特征的数据集应用子空间聚类，以寻找数据集的子空间结构并对其进行聚类。

计算机视觉中的许多问题与由多个不同视图的特征集表示的数据有关，不同的特征集表示有关数据集不同且部分独立的信息。这些不同的特征可以从不同的角度来提供有用的信息，从而提高数据的聚类性能，多视图聚类是将这些特征集集成在一起来执行聚类。文献[12]提出多视图谱聚类模型，以集成异构视觉的特征来进行图像分类。文献[13]引入正则化多视图谱聚类，以在具有正则约束的同时对不同视图执行聚类。为了解决大规模多视图聚类问题，文献[14]提出了多视图K-means聚类方法。文献[9]提出一种基于结构化稀疏学习的多视图聚类方法，以同时执行特征选择和多视图聚类。但是，这些方法仅直接关注于聚类，而不是挖掘数据特征所隐藏的结构。本文提出一种新颖的多视图子空间聚类模型，对不同视图的特征进行降维以获得各自的低维子空间表示，然后把各个视图的低维子空间表示融合映射到一个共享的公共子空间表示，从而获得多视图一致的低维子空间表示。简单来说，就是从单个的视图数据特征学习一个低维子空间表示，再将多个视图的低维子空间表示融合学习到一个一致的低维子空间表示，把融合得到的子空间表示进行谱聚类。在3个基准数据集上的对比实验结果证明了所提出方法的有效性。

1 相关工作 1.1 子空间聚类

很多数据集的数据分布于底层的低维子空间中，而不是均匀分布于整个空间。因此，数据点可以由低维子空间来进行表示。在获得数据集的低维子空间结构后，可以基于子空间表示来进行聚类而不是通过对整个空间执行聚类。通用的子空间聚类公式可以表示为

$ \mathop {\min }\limits_\mathit{\boldsymbol{Z}} \alpha \mathit{\boldsymbol{L}}(\mathit{\boldsymbol{X}},\mathit{\boldsymbol{XZ}}) + \Omega (\mathit{\boldsymbol{Z}}),{\rm{ s}}{\rm{. t}}{\rm{. }}0 \le {Z_{i,j}} \le 1,{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},\alpha > 0, $

(1)

式中：标量α>0是重构误差的权重系数；q是全为1的列向量，Z^Tq=q是指子空间表示Z的每列和为1；L(X, XZ)和Ω(Z)分别表示重构损失函数和正则化项，通常会根据不同的假设来进行定义。例如，稀疏子空间聚类^[9]是基于$\ell $₁-norm在无限多个可能的表示中搜索最稀疏的表示；低秩表示聚类^[15]试图揭示具有低秩表示的聚类结构；平滑表示聚类^[16]深入分析了基于自我表示方法的分组效果。基于子空间表示矩阵Z，一般会用W=$\frac{1}{2}$(|Z|+|Z^T|)来构造相似度矩阵。而后，基于相似度矩阵W，通常对其执行谱聚类算法来得到最终的聚类结果^{[9, 15-16]}。

1.2 多视图子空间聚类

在子空间聚类中组合多个视图的特征是很具有挑战性的，较为直接的方法是将所有视图的特征串联在一起，然后对所串联的特征执行聚类。但是在这种方法中，信息量更多的视图和信息量较少的视图将被同等对待，因此解决方案不是最佳的。还有另外一种多视图子空间聚类方式，是对原始的多个视图的数据特征进行融合得到一个视图，然后再对这个视图进行子空间聚类。本文则提出一种直接对每个视图的低维子空间表示进行融合的多视图子空间聚类方法。

2 多视图子空间聚类算法 2.1 基于子空间融合的多视图聚类模型的建立 2.1.1 多视图子空间表示的建立

给定数据集X=[X¹, X², …, X^m]^T∈R^d×n，其中d=$\sum\limits_{v = 1}^m {{d_v}} $，d_v是第v个视图中特征的维度；X^v∈R^d_v×n表示第v个视图中的特征(v=1, 2, …, m，总共有m个视图)。如果在每个单视图上执行子空间学习，即可获得第v个视图的子空间表示Z^v，Z^v中的非零元素对应于来自同一子空间的数据点。利用通用的子空间聚类方法模型，可以得到多视图数据的每个视图所对应的子空间表示，即

$ \min \alpha \sum\limits_{v = 1}^m {\left\| {{\mathit{\boldsymbol{X}}^v} - {\mathit{\boldsymbol{X}}^v}{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \sum\limits_{v = 1}^m {\left\| {{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} ,{\rm{s}}.{\rm{t}}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le Z_{i,j}^v \le 1,{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},\alpha > 0 。$

(2)

2.1.2 子空间表示融合

在式(2)中，每个视图都可以得到一个各自的子空间表示矩阵Z^v。但是在多视图聚类中，数据原本的分布是一致的，相似的样本属于同一个簇，并且不同视图之间的子空间表示矩阵应具有一致结构。因此，将所有子空间表示矩阵融合为一个公共的子空间表示，使得公共的子空间表示能够综合所有视图子空间所包含的数据分布结构，其数学表示式为

$ \begin{array}{*{20}{l}} {\mathop {\min }\limits_{\mathit{\boldsymbol{Z}},{\mathit{\boldsymbol{Z}}^v},{r_v}} \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2,} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}0 \le Z_{i,j}^v \le 1,{{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},0 \le {Z_{i,j}} \le 1,{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1,} \end{array} $

(3)

式中：r_v是每一个视图的子空间表示矩阵的权重。虽然每一个视图的数据分布是一致的，但是一般会侧重于不同的数据。这m个子空间表示可能存在着一些共有的数据点分布结构，也会有每个视图所独有的数据点分布结构。因此，将所有视图的子空间表示矩阵以不同的权重融合起来，得到一个公共的子空间表示矩阵Z，使其尽可能包含数据的所有簇的分布情况。

一个好的聚类结构一般会具有一个性质，就是邻接矩阵中连通分量的数目和最终聚类的簇的数目相等。根据文献[17]可知，相似度矩阵中连通分量的个数等于其对应的拉普拉斯矩阵中0特征值的个数。假设数据集中簇的个数为k, 则相似度矩阵所对应的拉普拉斯矩阵中0特征值的个数等于k才是最好的结果，用数学方式表示为rank(L)=n-k。将这个约束加入(3)，使得到的公共子空间表示矩阵Z具有上述性质。一般来说，秩的约束会让优化问题变得很难求解。根据Ky Fan定理可得$\sum\limits_{i = 1}^k {{\sigma _i}\left( \mathit{\boldsymbol{L}} \right)} $=arg min Tr(F^TLF^v)，其中σ_i(L)为L的第i小的特征值。显而易见，L的秩等于n-k意味着$\sum\limits_{i = 1}^k {{\sigma _i}\left( \mathit{\boldsymbol{L}} \right) = 0} $。将以上约束加入式(3)后的结果为

$ \begin{array}{*{20}{l}} {\min \alpha \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \beta {\mathop{\rm Tr}\nolimits} \left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{LF}}} \right),}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}0 \le Z_{i,j}^v \le 1,{{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},0 \le {Z_{i,j}} \le 1,{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1,{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{I}},} \end{array} $

(4)

式中：L=D-$\frac{1}{2}$(Z+Z^T)，D是Z的度矩阵，其对角线的第i个元素${D_{i, i}} = \sum\limits_{j = 1}^n {{Z_{i, j}}} $。

2.1.3 目标函数

将式(2)和式(4)相结合，可以得到整个算法的框架为

$ \begin{array}{*{20}{l}} {\mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^v},\mathit{\boldsymbol{Z}},{r_v}} \alpha \sum\limits_{v = 1}^m {\left\| {{\mathit{\boldsymbol{X}}^v} - {\mathit{\boldsymbol{X}}^v}{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \beta {\mathop{\rm Tr}\nolimits} \left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{LF}}} \right),}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}0 \le Z_{i,j}^v \le 1,{{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},\alpha > 0,\beta > 0,0 \le {Z_{i,j}} \le 1,{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}},0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1,{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{I}}} 。\end{array} $

(5)

式(5)中第1项是构造每个视图的子空间表示，第2项是子空间的融合过程，第3项是公共子空间表示的拉普拉斯矩阵的构造。通过这种方式，融合得到的公共子空间表示矩阵可以综合各个视图的子空间表示，并且能够尽可能照顾到各个子空间所独有的数据簇的分布，使得聚类效果达到最好。

2.2 优化过程 2.2.1 固定Z^v、r_v, 优化Z

忽略其他无关项，目标函数的优化式可以转化为

$ \mathop {\min }\limits_\mathit{\boldsymbol{Z}} \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \beta {\mathop{\rm Tr}\nolimits} \left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{LF}}} \right),{\rm{s}}.{\rm{ t}}{\rm{. }}0 \le {Z_{i,j}} \le 1,{\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}} 。$

(6)

因为Z^v、r_v是固定的，故可令$\mathit{\boldsymbol{G}} = \sum\limits_{v = 1}^m {{r_v}{\mathit{\boldsymbol{Z}}^v}} $，对式(6)进行元素展开，可得

$ \mathop {\min }\limits_{{Z_{i,j}}} {\left( {{Z_{i,j}} - {G_{i,j}}} \right)^2} + \beta {\left\| {{\mathit{\boldsymbol{f}}_i} - {\mathit{\boldsymbol{f}}_j}} \right\|^2}{Z_{i,j}}, $

(7)

式中：f_i是F的第i行。再通过对Z_{i, j}求导并令导数为0，可以得到Z_{i, j}的闭式解为

$ {Z_{i,j}} = \frac{1}{2}\left( {2\mathit{\boldsymbol{G}} - \beta {{\left\| {{\mathit{\boldsymbol{f}}_i} - {\mathit{\boldsymbol{f}}_j}} \right\|}^2}} \right) 。$

(8)

2.2.2 固定Z^v、Z, 优化r_v

忽略其他无关项，目标函数的优化式可以转化为

$ \mathop {\min }\limits_{{r_v}} \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} ,{\rm{s}}.{\rm{ t}}{\rm{. }}0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1 。$

(9)

易知式(9)可以等价为

$ \mathop {\min }\limits_{{r_v}} \sum\limits_{v = 1}^m {\sum\limits_{c = 1}^m {{r_v}} } {r_c}{\mathop{\rm Tr}\nolimits} \left( {{{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{Z}}^c}} \right) - 2\sum\limits_{v = 1}^m {{r_v}} {\mathop{\rm Tr}\nolimits} \left( {{{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Z}}} \right),{\rm{s}}.{\rm{ t}}{\rm{. }}0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1 。$

(10)

令M=Tr((Z^v)^TZ^c)，则M∈R^m×m。令f=Tr((Z^v)^TZ)，则f∈R^m×1。故式(10)可以等价为

$ \mathop {\min }\limits_{{r_v}} {\mathit{\boldsymbol{r}}^{\rm{T}}}\mathit{\boldsymbol{Mr}} - 2{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{r}},{\rm{s}}.{\rm{ t}}{\rm{. }}0 \le {r_v} \le 1,\sum\limits_{v = 1}^m {{r_v}} = 1, $

(11)

式中：r=[r₁, r₂, …, r_m]^T∈R^m×1。易知，这个问题可以通过求解QP问题得到r的最优解。

2.2.3 固定Z、r_v, 优化Z^v

忽略其他无关项，目标函数的优化式可以转化为

$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^v}} \sum\limits_{v = 1}^m {\left\| {\mathit{\boldsymbol{Z}} - \sum\limits_{v = 1}^m {{r_v}} {\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} + \alpha \sum\limits_{v = 1}^m {\left\| {{\mathit{\boldsymbol{X}}^v} - {\mathit{\boldsymbol{X}}^v}{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2} ,{\rm{ s}}{\rm{.t}}{\rm{. }}0 \le Z_{i,j}^v \le 1,{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}} 。$

(12)

因为Z^v的优化只跟第v个视图的子空间表达有关，可令$\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{Z}} - \sum\limits_{c = 1, c \ne v}^m {{\mathit{\boldsymbol{r}}_c}{\mathit{\boldsymbol{Z}}^c}, \mathit{\boldsymbol{B}} = \alpha } \sum\limits_{c = 1, c \ne v}^m {\left\| {{\mathit{\boldsymbol{X}}^c} - {\mathit{\boldsymbol{X}}^c}{\mathit{\boldsymbol{Z}}^c}} \right\|_F^2} $。故式(8)可以等价为

$ \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}^v}} \left\| {\mathit{\boldsymbol{A}} - {r_v}{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2 + \alpha \left\| {{\mathit{\boldsymbol{X}}^v} - {\mathit{\boldsymbol{X}}^v}{\mathit{\boldsymbol{Z}}^v}} \right\|_F^2 + \mathit{\boldsymbol{B}},{\rm{s}}.{\rm{ t}}{\rm{. }}0 \le Z_{i,j}^v \le 1,{\left( {{\mathit{\boldsymbol{Z}}^v}} \right)^{\rm{T}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{q}} 。$

(13)

对式(13)进行展开并求导，可得Z^v的优化结果为

$ {\mathit{\boldsymbol{Z}}^v} = {\left( {r_v^2\mathit{\boldsymbol{I}} + \alpha {{\left( {{\mathit{\boldsymbol{X}}^v}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{X}}^v}} \right)^{ - 1}}\left( {{r_v}\mathit{\boldsymbol{A}} + \alpha {{\left( {{\mathit{\boldsymbol{X}}^v}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{X}}^v}} \right) 。$

(14)

多视图子空间聚类算法的流程如下。

输入：样本{X^v}_v=1^m，聚类个数k，超参数α、β。

输出：聚类标签矩阵Y。

初始化：初始化Z^v、Z，初始化r使得每个视图子空间表示矩阵所占权重相等，随机正交初始化F。

1 判断是否收敛；

2 通过解式(8)来优化Z；

3 通过解式(11)来优化r；

4 通过解式(14)来优化Z^v；

5 循环直至目标函数值收敛；

6 将融合得到的公共子空间表示Z输入到谱聚类中，最终返回聚类标签矩阵Y。

每种视图数据的样本数为n，算法的时间复杂度为O(n³)。

3 实验结果及分析 3.1 数据集和对比算法

在3个广泛使用的数据集上进行了实验评估，这3个数据集为Caltech101-7数据集^[18]、bbcsport_seg14of4数据集^[19]以及WebKB数据集^[20]。Caltech101-7是图像数据集Caltech101广泛使用的子集，在此子集中有7个类别，并且从这7个类别中总共选择了1 474张图像，每个样本提取了6个视图；bbcsport_seg14of4是图像数据集BBCsports的一个子集，包含4个视图、5个类别，每个类别选取了116个样本；WebKB数据集包含1 051个来自4所大学的网页，相应的标记分类为教授、学生、项目或其他网页，共有2个视图，此数据集的目的是开发一个反映万维网内容的概率性、象征性知识库，使网络上的文本信息以计算机可理解的形式提供，从而实现更复杂的信息检索和问题解决方案。

4种对比算法如下：MLRR_Con^[8]是一种基准方法，直接将多个视图的特征拼接在一起，然后对其执行K-means得到最终结果；Co-reg^[12]使用协同正则化方法，使得不同视图的划分达成一致，这里对比其中的“成对”方法；RMKMC^[21]通过获得共同的聚类指示矩阵并引入${\ell _{2, 1}}$范数，使得该方法对输入数据的异常值具有鲁棒性；FMR^[22]通过希尔伯特-史密斯独立性准则构造包含互补和一致信息的潜在表示，然后对潜在表示进行数据重建得到子空间表示。这4种算法均按照文献中所推荐的参数范围进行网格搜索并选取最好的结果。

3.2 实验结果分析

本文使用准确率(ACC)、调和平均数(F-score)和纯度(P)3个指标来衡量聚类的效果。不同算法在Caltech101-7、bbcsport_seg14of4、WebKB数据集下的性能结果如表 1所示。可以看出，在大多数情况下，直接对特征进行串联拼接的MLRR_Con方法的性能最差，本文算法在3个真实数据集下ACC、F-score和P值均为最高。这说明多视图聚类算法对探索不同视图之间的互补信息的确是可行的。

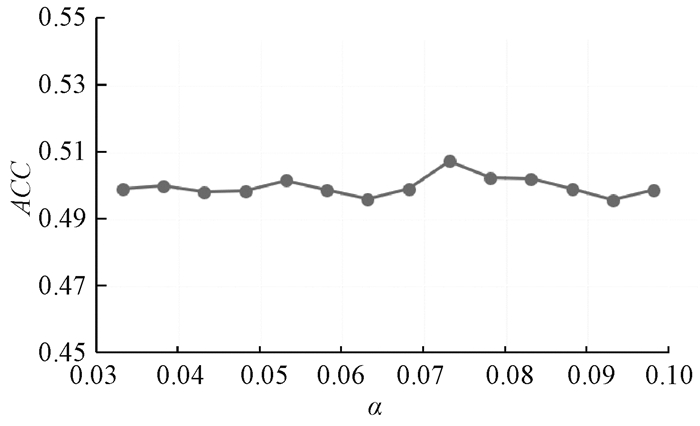
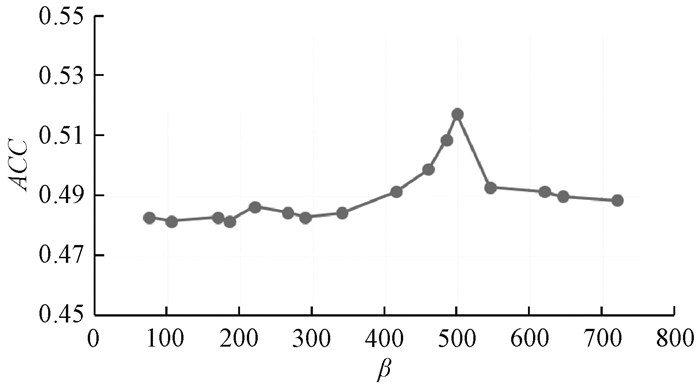
以bbcsport_seg14of4数据集为例，对两个超参数进行敏感性分析。初始化参数β值为100，参数α值的敏感性分析结果如图 1所示。可以看出，在0.03~0.10区间内，α值波动不大，ACC值对于α值敏感度不高，α值约等于0.072时ACC值最高。α值为0.072，对参数β值进行敏感性分析，结果如图 2所示。可以看出，β值为500左右时ACC值最高。β值对于ACC值的影响稍大，因此取一个比较好的β值对于实验结果会有所提升。

4 小结

本文提出了一种新颖的多视图子空间聚类模型。为了利用不同视图的互补信息，分别对各个视图执行子空间表示，然后将它们统一起来得到公共的子空间表示，再将公共的子空间表示进行谱聚类。本文模型充分利用了不同子空间表示所隐藏的数据簇的分布信息，这与之前的直接对原始数据进行融合的方法不同。后续研究将在以上工作的基础上继续开展，考虑大规模数据并将低秩表示算法引入模型中。