2. 常熟理工学院 计算机科学与工程学院 江苏 常熟 215500
2. School of Computer Science and Engineering, Changshu Institute of Technology, Changshu 215500, China
近年来,随着网络技术的不断进步,互联网逐渐渗透到生活的各个层面,人类社会活动逐渐网络化。生物网络[1]、航班网络[2]、推荐网络[3]、网络舆情监控[4]等都可以抽象为由节点和边构成的复杂网络。而复杂网络非同质的拓扑结构决定了网络本身的复杂程度, 少许关键节点的丢失会导致整个复杂网络稳定性失效。因此,挖掘复杂网络中的关键节点,有助于理解复杂网络的演化机制。
带有抽象时间信息的网络称作时序网络(temporal network),时序网络在高效捕获复杂网络节点交互关系上有着重要意义[5]。在针对时序网络关键节点的识别问题中,研究方法大致从两方面出发:从局部或者全局单个指标和因素获取节点的重要性排名;将多个指标融合获取节点的重要性排名。
关于第一类方法,Kim等[6]将动态网络建模为时间有序的有向图,简化成静态图,提出了基于有序图的时序接近中心性的算法。邓冬梅等[7]在基于静态网络上使用节点边缘贡献值评价节点重要性的基础上,提出节点的具体感染方式,并考虑了网络的时间属性,同时提出了时序网络中重要节点的排序方法。Ye等[8]提出了K-shell分解方法,将时序网络构建成加权网络,并且切分成m个时间切片。Huang等[9]提出的动态敏感中心性的基础上考虑节点的传播动力学,将动态中心性概念扩展到时间网络来对节点进行排序。Qu等[10]提出了时序网络的时间信息收集(TIG)过程,并且认为节点的重要性与时序信息有关系。Zhan[11]提出一种信息扩散模式GB,认为具有时间特征的节点对更容易出现在扩散轨迹中。
多个指标融合获取节点的重要性排名比单个指标更加合理,效率更高。Taylor等[12]用多层耦合分析的方法,将时序网络按层内关系和层间关系建立超邻接矩阵(supra-adjacency matrix, SAM),并定义了基于特征向量的中心性指标和节点重要性评价指标。但SAM方法将节点的层间关系定义为一个不可改变的参数,忽略了不同节点层间关系的差异性。Yang等[13]在此基础上将各层之间的连接用邻居拓扑重叠系数表示,提出了基于节点层间相似性的超邻接矩阵(similarity-based supra-adjacency matrix, SSAM)时序网络构建方法,同样结合层内关系和层间关系来求得时序网络的节点重要性排序。Lv等[14]提出基于PageRank中心度的层间相似度,计算多层时态网络中每层的PageRank中心度向量,然后通过计算PageRank中心度向量的距离来定义任意两层之间的相似度。Yan等[15]提出一种多信息随机游走的方法(IFMNE),其融合了节点信息和网络拓扑信息,同时考虑节点公共邻居的数量和聚类系数,相比之前的研究,最大限度地保留了节点的网络特征。Jiang等[16]提出一种引入衰减因子的层间度量指标(enhance-similarity index, ESI),还提出基于层间耦合强度衰减的超邻接矩阵(attenuation based supra-adjacency matrix, ASAM) 时序网络建模方法。
然而,上述节点重要性的研究主要集中在无权时序网络上,对于节点同时受到链接强度和时间属性的研究比较少。针对这一问题,本文提出一种更通用和符合实际的模型。首先,结合多层网络的局部交互强度和拓扑变化,提出了一种新的多指标交互算法来度量相邻和非相邻时间层之间的耦合关系;然后,基于时间因素对权重的影响,提出一种新的层内邻间矩阵,综合层内和层间关系建立了加权超邻接矩阵(weighted supra-adjacency matrix, WSAM)模型。同时,考虑到多个指标的偏重比例对层间耦合强度有不同影响,引入了偏重系数来更准确地描述不同时间层节点的耦合强度。
1 理论基础 1.1 加权时序网络定义给定一个无向加权网络模型为三元组G={V, E, W},其中:V={v1, v2, …, vn}、E={e1, e2, …, et}分别表示节点与边的集合;t表示两个节点建立连接的时间,即在t时刻,节点vi与节点vj之间出现连边;(vi, vj)∈E表示从节点vi到节点vj的连边。无向加权网络的邻间矩阵满足wij=wji。
1.2 时序网络层内关系分析经典的模型在对层内节点交互关系描述时,只考虑边是否存在,而没有考虑链接强度,本文提出时近分数来描述层内边的链接概率。
定义1(时近分数) 一个人在较近时间内与之互动的接触可能比距离较远时间内形成的交互更重要。时近分数是一个在区间[0, 1]的实数TScore(k),
| $ T_{\text {Score }}(k)=2^{-\sigma(T-k)}, $ | (1) |
其中:k为当前时间窗口; σ为变量参数。
定义2(基于时近分数的链接强度) 总的链接强度计算公式为
| $ T_{\text {Strength }}\left(w_{i j}\right)=T_{\text {Score }}(k) w_{i j}, $ | (2) |
其中:wij为节点真实权值。设WΓ为总的链接强度矩阵,记录两个节点交互的链接强度变化,即
| $ \boldsymbol{W}^{{\mathit{\Gamma}}}=T_{i j}=T_{\text {Strength }}\left(w_{i j}\right), $ | (3) |
链接强度矩阵作为层内邻间矩阵,进行后面的模型嵌入。
1.3 时序网络层间关系分析在无权时序网络中,共同邻居指标[17]、资源分配指标[18]、优先链接指标[19]经常被作为层间耦合关系指标,但不能直接应用于加权时序网络,而文献[20]认为在这三个相似性指标中,优先链接(preferential attchment,PA)指标所挖掘出来的重要节点准确度高,因此,本文将PA指标改进成适应于加权时序网络的加权优先链接指标,并将其作为一种基准算法与本文算法对比。
定义3(WPA指标) 加权优先链接(WPA)指标指两个节点之间产生新链接的概率正比与两个节点的强度的乘积,
| $ W P A_{j}=\sum\limits_{i, j \in {\mathit{\Gamma}}(t)} w_{i j}^{t} \sum\limits_{i, j \in {\mathit{\Gamma}}(t+1)} w_{i j}^{t+1}, $ | (4) |
定义4(多指标交互算法) 多指标交互算法(TWCR)将共同邻居指标和资源分配指标融合,将节点的时间属性考虑进去,同时考虑节点的自身邻居节点和两个时间层节点的公共邻居节点,定义为
| $ TWCR_{j}^{(t, t+1)}=\alpha TWCN(j)+(1-\alpha) T W R A(j), $ | (5) |
| $ {TWCN}_{(j)}=\sum\limits_{j \in\left({\mathit{\Gamma}}_{i}^{t} \cap {\mathit{\Gamma}}_{i}^{t+1}\right)} T_{i j}^{t} T_{i j}^{t+1}, $ | (6) |
| $ TWRA_{(j)}=\sum\limits_{j \in\left({\mathit{\Gamma}}_{i}^{t} \cap {\mathit{\Gamma}}_{i}^{t+1}\right)} \frac{I}{\min \left(T_{i j}\right)}, $ | (7) |
其中:当α>I/2时,节点的自身邻居的交互被认为对节点的重要性影响程度更大;当α < I/2时,节点的共同邻居的交互被认为对节点的重要性影响程度更大[21]。
2 加权时序网络模型构建经典时序网络模型在表示不同时间层网络间关系中使用了相同的参数, 忽略了不同节点层间连接关系的差异性。对于一个中心节点,其中一个邻居节点进行信息传播时,在考虑该邻居节点本身的交互频率时,还应该把时间因素考虑进去。因此,针对SAM模型存在的问题,同时对层内节点关系和层间节点关系进行改进,提出改进的WSAM模型。
2.1 SAM时序网络模型文献[12]基于时序网络模型的多层耦合关系, 提出了经典的SAM时序网络模型。
| $ \boldsymbol{S} \boldsymbol{A} \boldsymbol{M}=\left[\begin{array}{cccc} A^{(1)} & \omega I & 0 & \cdots \\ \omega I & A^{(2)} & \omega I & \cdots \\ 0 & \omega I & & \ldots \\ \cdots & \cdots & \cdots & A^{({\mathit{\Gamma}})} \end{array}\right], $ | (8) |
其中:A(1)、A(2)、…、A(T)表示层内连接关系,这里用等距切分的Γ个时间层网络对应的邻接矩阵表示,依次位于SAM模型的对角线上。
2.2 改进时序网络模型由以上分析可知,节点之间的影响程度同时受到节点所在时间段、节点与近邻节点的交互强度、节点与跨层节点的交互强度的多重制约,因此,我们提出了WSAM网络模型,其具体表示形式为
| $ \boldsymbol{W S A} \boldsymbol{M}=\left[\begin{array}{cccc} W^{(1)} & R^{(1, 2)} & \cdots & R^{(1, n)} \\ R^{(1, 2)} & W^{(2)} & \cdots & R^{(2, n)} \\ \vdots & \vdots & & \vdots \\ R^{(1, n)} & R^{(2, n)} & \cdots & W^{({\mathit{\Gamma}})} \end{array}\right], $ | (9) |
其中:W(1)、W(2)、…、W(Γ)表示Γ个时间层对应的层内关系,R(1, 2)、R(2, 3), …表示相邻层之间的耦合关系,R(1, 3)、R(2, 4), …表示非相邻层之间的耦合关系。层内邻接矩阵WΓ的表示形式为
| $ \boldsymbol{W}^{{\mathit{\Gamma}}}=\left[\begin{array}{cccc} 0 & T_{12} & \cdots & T_{1 n} \\ T_{12} & 0 & \cdots & T_{2 n} \\ \vdots & \vdots & & \vdots \\ T_{1 n} & T_{2 n} & \cdots & 0 \end{array}\right] 。$ | (10) |
图 1给出一个加权时序网络模型的构建。
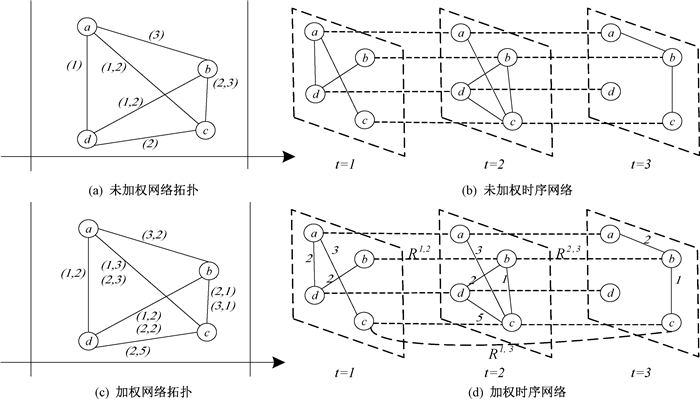
|
图 1 加权时序网络模型构建 Fig. 1 Construction of weighted temporal network model |
为了衡量节点排序的准确性, 本文选取特征向量中心性作为节点重要性排序方法。根据加权超邻接矩阵求其主特征值对应的特征向量v={v1, v2, v3, …, vnt}Γ,则向量v的第n(t-1)+i项表示节点i在第t个时间切片上的特征向量中心性,将其记为n×t的矩阵F={fit}n×t,定义为
| $ f_{i t}=v_{n(t-1)}+i。$ | (11) |
节点重要性不仅体现在网络对信息的传播能力, 也体现在节点被移除后对网络连通的破坏性[8]。时序最大连通分量[16]是衡量网络连通性的一个重要方法,定义为
| $ LCC=\frac{1}{m} \sum\limits_{t=1}^{m} \frac{\max\limits_{1 \leqslant i \leqslant k}|n|_{i}^{t}}{N}, $ | (12) |
其中:|n|it表示第t个时间切片中第i个连通子图中的节点数目;k表示图中连通分量的数目;LCC∈[0, 1]。由于节点的移除会破坏网络的连通性和鲁棒性,随着一部分节点的删除,时序网络最大连通分量越小,表明删除的节点对网络连通性的破坏越大,则该节点越重要。反之,节点的重要性较弱。
3.2.2 性能变化为了更直观地描述本文所提出方法的效果,通过删除一定比例的节点后利用公式(13)计算网络的性能变化[26],定义为
| $ E=\left(e(N)-e\left(\frac{q}{N}\right)\right) /(e(N)), $ | (13) |
其中:e(N)表示未删除节点前的时序网络性能;e(q/N)表示累积删除q比例后的时序网络性能,E的值越大,说明删除的节点对网络性能的影响越大,评价方法越准确。
3.2.3 容错性分析容错性指标[27]反映了某种指标下节点排序的准确性,定义为
| $ I(f)=\sum\limits_{i=1}^{n}\left|f_{i}^{\prime}-f_{i}\right|_{t}, $ | (14) |
其中:fi和fi′分别是由原图和修改后的图得到的特征向量中心性排序,其值越小,排序越准确。
4 实验数据及分析 4.1 实验数据在本文实验中,我们采用Workspace[28]、Email[29]和StarWars这三个真实的动态社交网络数据集进行实验结果验证。三个数据集的基本信息如表 1所示。
|
|
表 1 数据集基本信息 Tab. 1 Basic information of datasets |
为了验证本文算法的效果,基于上述三个数据集,分别与SAM、SSAM和WPA方法进行实验对比,同时验证我们的算法优于未加权的算法和加权算法。
如图 2所示,q为删除比例,取变量σ=1,Workspace网络、Email网络、StarWars网络的最大连通分量变化情况。Workspace网络中,分别删除各个时间切片中特征向量中心性排名前15、20、30的节点。Email网络中,分别删除各个时间切片中特征向量中心性排名前20、30、40的节点。StarWars网络中,分别删除各个时间切片中特征向量中心性排名前5、10、15的节点。在三个网络中,本文算法的最大连通分量都明显下降,其中在Email网络中的效果最为明显。而WPA方法得到的时序网络最大连通分量普遍高于SAM方法或者SSAM方法所得到的结果,进一步说明简单的加权并不能有效提升网络的性能,反而可能会影响网络的连通性。
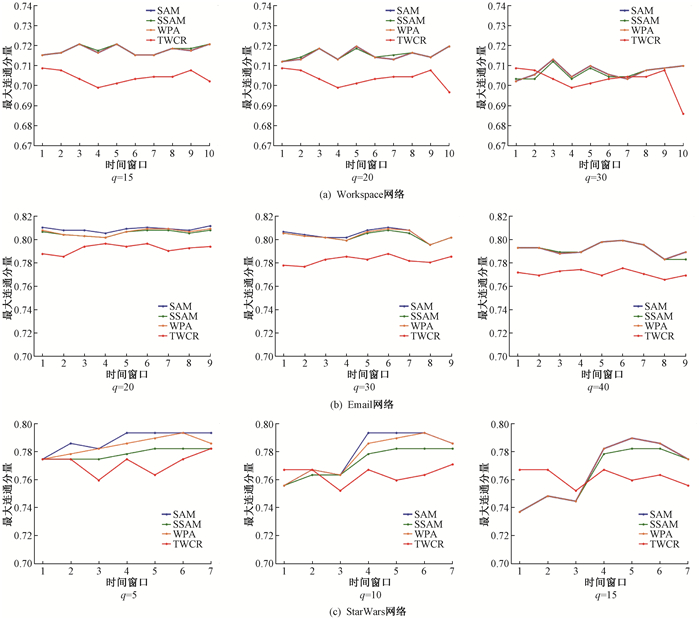
|
图 2 不同网络中的LCC变化情况 Fig. 2 LCC changes of different networks |
图 3分别展示了Workspace网络、Email网络、StarWars网络随着删除比例q的递增,网络的各个时间切片的性能变化情况。从图 3可以看出来,用WSAM模型构建的加权时序网络对应的性能明显强于基准算法,在三个数据集的时间切片上,本文方法的性能总体上高于对比算法。Workspace网络中,删除排名前20、30的节点,本文方法和SAM方法、SSAM方法、WPA方法相比,效果最为明显。StarWars网络中,在时间窗口3以后,性能开始提高,当删除前15的节点后,时间窗口为1和2时,性能低于基准算法,可能是由于实际数据的影响造成的。
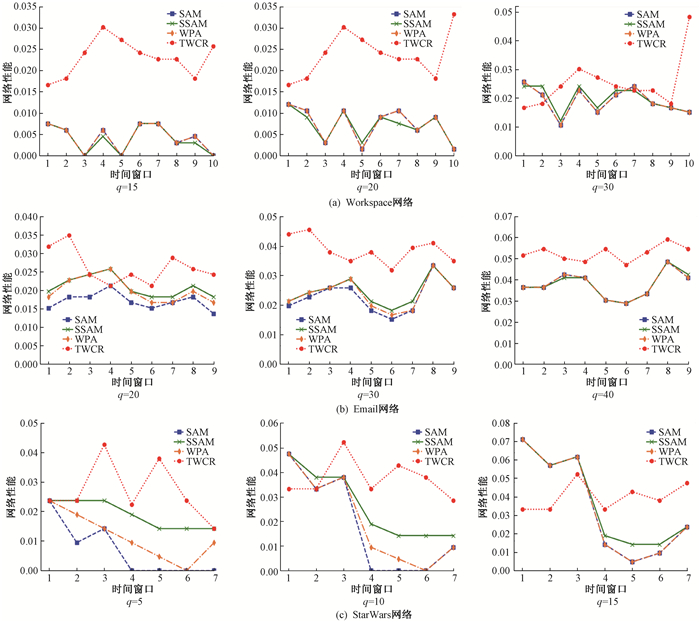
|
图 3 不同网络中的性能变化 Fig. 3 Performance changes of different networks |
在StarWars网络中,变量σ=1和σ=4时,使用公式(14)与WPA算法进行容错性比较,实验结果如表 2所示。
|
|
表 2 StarWars网络I(f)值 Tab. 2 I(f) value of StarWars network |
从表 2可以看出本文提出的WSAM模型,随着变量取不同值,与WPA算法相比,整体上I(f)值略小。说明本文算法的排序结果更准确,要比直接使用权重更适用社交网络。
5 结束语本文结合节点与节点的层内关系与层间关系提出一种新的多指标交互算法,着重考察节点交互链接强度对网络结构的影响,同时构建了基于多指标交互算法的超邻接矩阵模型。实验证明移除部分节点后造成网络连通性更大程度的下降和网络性能大幅度提升、容错性更强,说明该方法可以更为恰当地描述时序网络,从而更准确地识别关键节点。
然而,本文针对节点之间权重的设计需要更为准确的方法来描述。其次,如何将本文方法进一步扩展到有向加权的时序网络也是一个亟待解决的问题。
| [1] |
PRASAD K, KHATOON F, RASHID S, et al. Targeting hub genes and pathways of innate immune response in COVID-19: a network biology perspective[J]. International journal of biological macromolecules, 2020, 163: 1-8. DOI:10.1016/j.ijbiomac.2020.06.228 (  0) 0) |
| [2] |
CHEN Y H, LIN J J. Determinants of flight delays at East Asian Airports from an airport, route and network perspective[J]. Journal of air transport management, 2021, 94: 102064. DOI:10.1016/j.jairtraman.2021.102064 (  0) 0) |
| [3] |
郭阳, 李全龙, 李骐. 基于学习者兴趣挖掘的个性化课程推荐方法[J]. 郑州大学学报(理学版), 2021, 53(4): 77-82. GUO Y, LI Q L, LI Q. Personalized course recommendation based on learner interest mining[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(4): 77-82. (  0) 0) |
| [4] |
何佳, 周长胜, 石显锋. 网络舆情监控系统的实现方法[J]. 郑州大学学报(理学版), 2010, 42(1): 82-85. HE J, ZHOU C S, SHI X F. Implementation method for network public opinion monitoring system[J]. Journal of Zhengzhou university (natural science edition), 2010, 42(1): 82-85. (  0) 0) |
| [5] |
GUNTURI V M V, SHEKHAR S, JOSEPH K, et al. Scalable computational techniques for centrality metrics on temporally detailed social network[J]. Machine learning, 2017, 106(8): 1133-1169. DOI:10.1007/s10994-016-5583-7 (  0) 0) |
| [6] |
KIM H, ANDERSON R. Temporal node centrality in complex networks[J]. Physical review E, statistical, nonlinear, and soft matter physics, 2012, 85(2): 026107. DOI:10.1103/PhysRevE.85.026107 (  0) 0) |
| [7] |
邓冬梅. 时序网络结构特性实证分析及研究[D]. 成都: 电子科技大学, 2014. DENG D M. The structure characteristics empirical analysis and research in temporal network[D]. Chengdu: University of Electronic Science and Technology of China, 2014. (  0) 0) |
| [8] |
YE Z H, ZHAN X X, ZHOU Y Z, et al. Identifying vital nodes on temporal networks: an edge-based K-shell decomposition[C]//201736th Chinese Control Conference (CCC). Piscataway: IEEE Press, 2017: 1402-1407.
(  0) 0) |
| [9] |
HUANG D W, YU Z G. Dynamic-Sensitive centrality of nodes in temporal networks[J]. Scientific reports, 2017, 7: 41454. DOI:10.1038/srep41454 (  0) 0) |
| [10] |
QU C Q, ZHAN X X, WANG G H, et al. Temporal information gathering process for node ranking in time-varying networks[J]. Chaos: an interdisciplinary journal of nonlinear science, 2019, 29(3): 033116. DOI:10.1063/1.5086059 (  0) 0) |
| [11] |
ZHAN X X, HANJALIC A, WANG H J. Information diffusion backbones in temporal networks[J]. Scientific reports, 2019, 9: 6798. DOI:10.1038/s41598-019-43029-5 (  0) 0) |
| [12] |
TAYLOR D, MYERS S A, CLAUSET A, et al. Eigenvector-based centrality measures for temporal networks[J]. Multiscale modeling & simulation: a SIAM interdisciplinary journal, 2017, 15(1): 537-574. (  0) 0) |
| [13] |
YANG J N, LIU J G, GUO Q, et al. Node importance idenfication for temporal network based on inter-layer similarity[J]. Acta physica sinica, 2018, 67(4): 048901. DOI:10.7498/aps.67.20172255 (  0) 0) |
| [14] |
LV L, ZHANG K, ZHANG T, et al. Eigenvector-based centralities for multilayer temporal networks under the framework of tensor computation[J]. Expert systems with applications, 2021, 184: 115471. DOI:10.1016/j.eswa.2021.115471 (  0) 0) |
| [15] |
YAN G H, LI Z, LUO H, et al. Multilayer network representation learning method based on random walk of multiple information[J]. IEEE access, 9: 53178-53189. DOI:10.1109/ACCESS.2021.3070318 (  0) 0) |
| [16] |
JIANG J L, FANG H, LI S Q, et al. Identifying important nodes for temporal networks based on the ASAM model[J]. Physica a: statistical mechanics and its applications, 2022, 586: 126455. DOI:10.1016/j.physa.2021.126455 (  0) 0) |
| [17] |
LORRAIN F, WHITE H C. Structural equivalence of individuals in social networks[J]. The journal of mathematical sociology, 1971, 1(1): 49-80. DOI:10.1080/0022250X.1971.9989788 (  0) 0) |
| [18] |
ZHOU T, LV L, ZHANG Y C. Predicting missing links via local information[J]. The European physical journal B, 2009, 71(4): 623-630. DOI:10.1140/epjb/e2009-00335-8 (  0) 0) |
| [19] |
MURATA T, MORIYASU S. Link prediction of social networks based on weighted proximity measures[C]//IEEE/WIC/ACM International Conference on Web Intelligence. Piscataway: IEEE Press, 85-88.
(  0) 0) |
| [20] |
ASSARI A, MAHESH T M, ASSARI E. Role of public participation in sustainability of historical city: usage of TOPSIS method[J]. Indian journal of science and technology, 2012, 5(3): 1-6. (  0) 0) |
| [21] |
YANG Y Z, WANG X, CHEN Y, et al. A novel centrality of influential nodes identification in complex networks[J]. IEEE access, 8: 58742-58751. DOI:10.1109/ACCESS.2020.2983053 (  0) 0) |
| [22] |
LIU J G, REN Z M, GUO Q, et al. Node importance ranking of complex networks[J]. Acta physica sinica, 2013, 62(17): 178901. DOI:10.7498/aps.62.178901 (  0) 0) |
| [23] |
ZHANG Z K, LIU C, ZHAN X X, et al. Dynamics of information diffusion and its applications on complex networks[J]. Physics reports, 2016, 651: 1-34. DOI:10.1016/j.physrep.2016.07.002 (  0) 0) |
| [24] |
LV L, ZHANG Y C, YEUNG C H, et al. Leaders in social networks, the Delicious case[J]. PLoS one, 2011, 6(6): e21202. DOI:10.1371/journal.pone.0021202 (  0) 0) |
| [25] |
GÉNOIS M, VESTERGAARD C L, FOURNET J, et al. Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers[J]. Network science, 2015, 3(3): 326-347. DOI:10.1017/nws.2015.10 (  0) 0) |
| [26] |
PARANJAPE A, BENSON A R, LESKOVEC J. Motifs in temporal networks[EB/OL]. (2017-02-01)[2022-06-10]. https://dl.acm.org/doi/pdf/10.1145/3018661.3018731.
(  0) 0) |
 2024, Vol. 56
2024, Vol. 56


