100多年以来, 湍流的研究无论是在它的实际应用方面还是在本质研究方面都取得了非常大的进步.最早的模型化思想是由Boussinesq在1872年提出的, 后来如Prandtl、Taylor、Von Karman等著名流体力学家的工作奠定了其理论基础.在此基础上随着流体力学的发展, 流体力学家们建立各种关于雷诺应力的模型假设, 使雷诺应力模型方程得以封闭[1].学者们面对计算复杂的雷诺应力模型, 追求更加可靠和高级的湍流模型, 但仍不能定量地给出和详细地描述复杂湍流流动的特性[1].工程应用的湍流研究主要是对实际流动与现存湍流模型进行对比, 找出不同模型之间的差异以及应用范围, 并在此基础上改进、提出新的模型并应用到实践中[1].现阶段运用最广泛的湍流模型主要有:Baldwin-Lomax零方程模型, SA一方程模型, SST两方程模型[2].由于计算中流动的模拟精度除了受所用格式精度的影响外, 还与选取的湍流模型相关, 因此对比分析不同种类的湍流模型在跨声速绕流中的模拟精确度及特性是十分有必要的.
本文以典型的ONERA-M6(M6)机翼为计算模型, 空间离散格式采用稳定性较好、计算精度较高、计算量小的Roe格式, 在时间离散上采用计算效率高、稳定性好的隐式LU SGS时间推进方法[2].将NS方程与应用广泛的SA、SST两种湍流模型分别耦合的结果与实验数据对比分析, 探究两种模型的计算精确度及气动力特性, 并验证该方法的可行性, 为今后计算流体力学模型的选取和更高准确度湍流模型的建立提供参考.
1 数值计算方法 1.1 控制方程在一般的直角坐标系下, 时间相关可压缩流动的三维Navier-Stokes无量纲化守恒型方程的一般形式为
| $ \frac{{\partial Q}}{{\partial t}} + \frac{{\partial E}}{{\partial x}} + \frac{{\partial F}}{{\partial y}} + \frac{{\partial G}}{{\partial z}} = \frac{1}{{{\mathop{\rm Re}\nolimits} }}(\frac{{\partial {E_v}}}{{\partial x}} + \frac{{\partial {F_v}}}{{\partial y}} + \frac{{\partial {G_v}}}{{\partial z}}), $ | (1) |
其中:Q为守恒型变量; E、F、G分别为无黏通量; Ev、Fv、Gv分别为黏性通量; Re为雷诺数.在Re湍流流动下, 只有补充计算湍流黏性系数的相关公式才能使方程(1)封闭[1-2].
本文计算方法是格心式有限体积法, 该方法能有效地避免差分方法固有的奇异性问题, 并且对网格质量的依赖程度相对较小, 边界条件处理起来也相对简单[2-3].无黏项采用稳定性较好、具有强的激波捕捉能力和高的分辨接触间断能力的Roe格式[3].为了提高格式的精度, 对单元左、右两侧网格面上的变量采用具有保单调性的MUSCL(monotone upstream centered scheme for conservation laws)插值, 为了消除激波附近非物理振荡, 采用了三阶迎风偏置修正限制器.时间推进采用隐式LU SGS方法[2].为了加快收敛速度, 提高计算效率, 采用了三重W循环的多重网格方法.边界条件主要使用物面边界、远场边界和块连接边界条件.
1.2 湍流模型 1.2.1 SA模型SA湍流模型[4-5]是针对简单流动而逐步补充发展起来的一方程模型, 核心是引入相关变量
| $ \begin{array}{l} \frac{{\partial \tilde w}}{{\partial t}} = \left( {0.1355} \right)[1 - {h_{t2}}]\tilde x\tilde w + \frac{1}{{2/3}}[\nabla \left( {\left( {w + \tilde w} \right)\nabla \tilde w} \right) + \\ \left( {0.622} \right){\left( {\nabla \tilde w} \right)^2}] - ({C_{v1}}{h_v}) - \frac{{0.1355}}{{{{\left( {0.41} \right)}^2}}}{h_{t2}}{\left( {\frac{{\tilde w}}{d}} \right)^2} + {h_{t1}}\Delta {U^2}, \end{array} $ |
其中:μL为湍流黏性系数, 计算公式为
| $ {\mu _L} = \rho \tilde w{h_{w1}}, {h_{w1}} = ({Y^3})/({Y^3} + C_{W1}^3), Y = \frac{{\tilde w}}{w}; $ |
w是分子黏性系数, 生成项为
| $ \tilde x = \mathit{\Omega } + \tilde w{h_{w2}}/{\left( {0.41} \right)^2}{d^2}, {h_{w2}} = 1 - Y/(1 + Y{h_{w1}}). $ |
SST模型[4, 6-8]通过引入混合函数把Wilcox模型和k-ω模型合并为一个模型.SST模型与Wilcox模型的湍流动能d方程相同, SST模型的湍流频率μ方程的表达式为
| $ \begin{array}{l} \frac{{\partial \left( {\rho \mu } \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}[\rho {v_j}\mu - (\omega + {\sigma _\mu }{v_T})] = \\ {T_\mu } - \alpha \rho {\mu ^2} + 2(1 - {H_1})\frac{{\rho \left( {0.856} \right)}}{\mu }\frac{{\partial k\partial \mu }}{{\partial {x_j}\partial {x_j}}}, \end{array} $ |
其中:湍流黏性系数ωT定义为ωT=min[ρk/μ, (0.31ρk)/(ΩH2)]; 生成项Tμ为Tμ=γρΩ2; 函数定义为
| $ \begin{array}{*{20}{c}} {{H_1} = \tanh ({\mathit{\Gamma }^4}), \mathit{\Gamma } = \min [\max ({\mathit{\Gamma }_1}, {\mathit{\Gamma }_3}), {\mathit{\Gamma }_2}], }\\ {{\mathit{\Gamma }_1} = \left( {500\mu } \right)/(\rho {y^2}\omega ), {\mathit{\Gamma }_2} = (4\rho {\sigma _{\omega 2}}k)/({y^2}(C{D_{k\omega }})), {\mathit{\Gamma }_3} = \sqrt k /\left( {0.99y\omega } \right).} \end{array} $ |
k-ω模型中的交叉扩散表达式为
| $ C{D_{k\omega }} = \max (\frac{{2\rho {\sigma _{\omega 2}}}}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}}, 1 \times {10^{ - 20}}). $ |
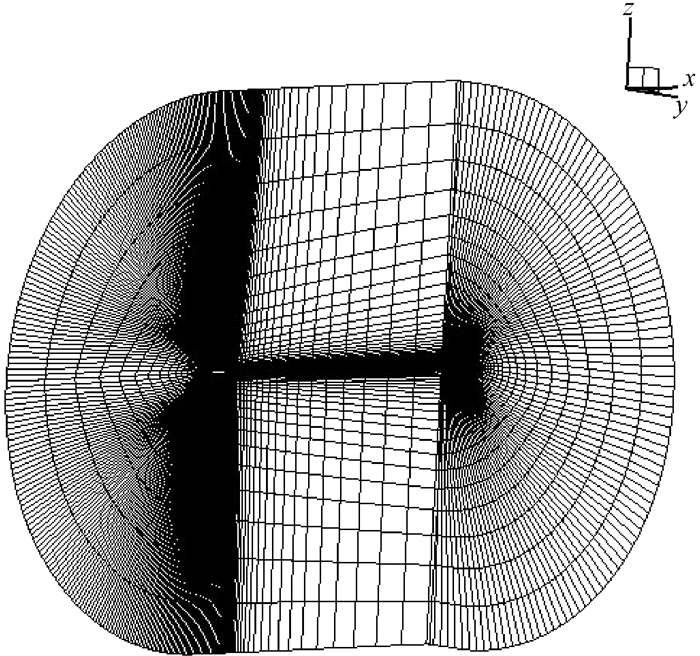
M6机翼与其他类型的机翼相比, 其几何外形简单, 机翼表面的绕流能表现出激波和局部超音速流动等各种复杂的流动状态, 常应用于CFD算法的测试和模型的检验[9].计算状态为M∞=0.839 4, 攻角α=3.06°, 雷诺数Re=1.814×107, 参考面积S=0.526 296 m2, 参考弦长c=0.646 070 m, 参考展长b=1.196 300 m, 采用的计算网格为“C-O”型的结构网格, 图 1和图 2分别表示M6机翼的表面网格和空间网格.本文分别进行了NS方程耦合SA模型和SST模型的湍流计算.并将计算结果与实验数据进行了比较.图 3表示M6机翼表面6个展向位置处的本文计算压力系数分布与实验数据的比较.

|
图 1 M6机翼表面网格 Fig. 1 The surface grid of M6 wing |
|
图 2 M6机翼空间网格 Fig. 2 The space grid of M6 wing |
|
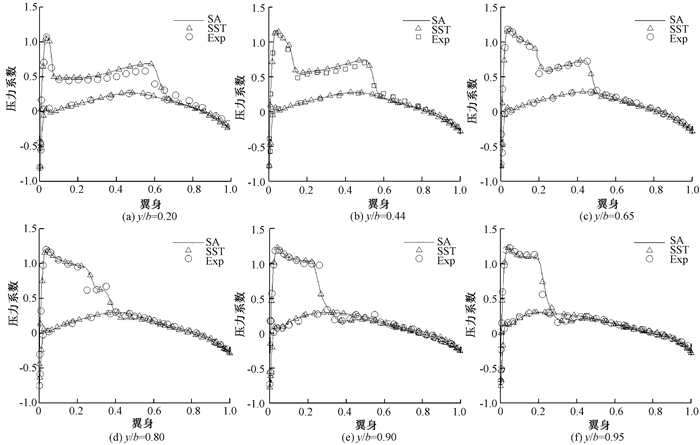
图 3 两种湍流模型压力系数分布的比较 Fig. 3 Comparison of pressure coefficient distribution of two turbulence models |
图 3中的结果表明两种模型预测的机翼表面激波位置和压力系数分布很接近.随着机翼表面展向位置由翼根向翼稍推移, 第1道激波向翼稍方向移动, 第2道激波向翼根方向移动, 在展向y/b=0.80位置处, 两道激波清晰可见.与实验结果相比, 两种模型预测到的第1道激波向后推的速度稍快, 第2道激波的位置与实验数据吻合较好.在展向y/b=0.90位置处, 两道激波几乎重叠.
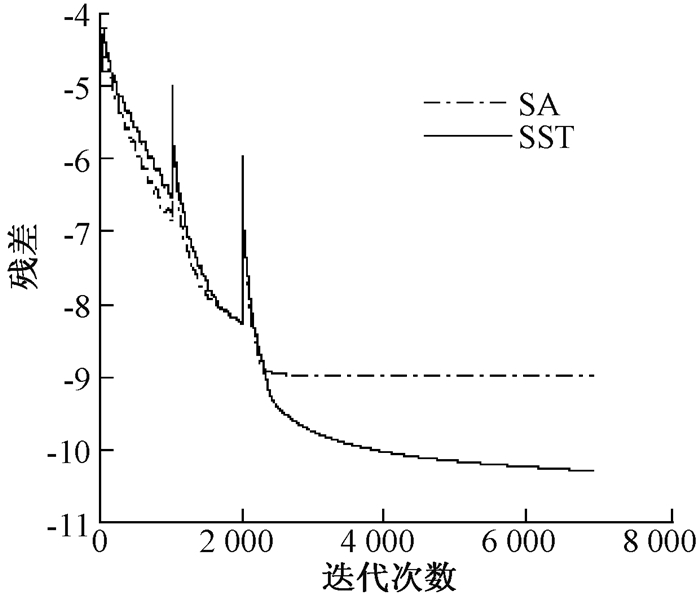
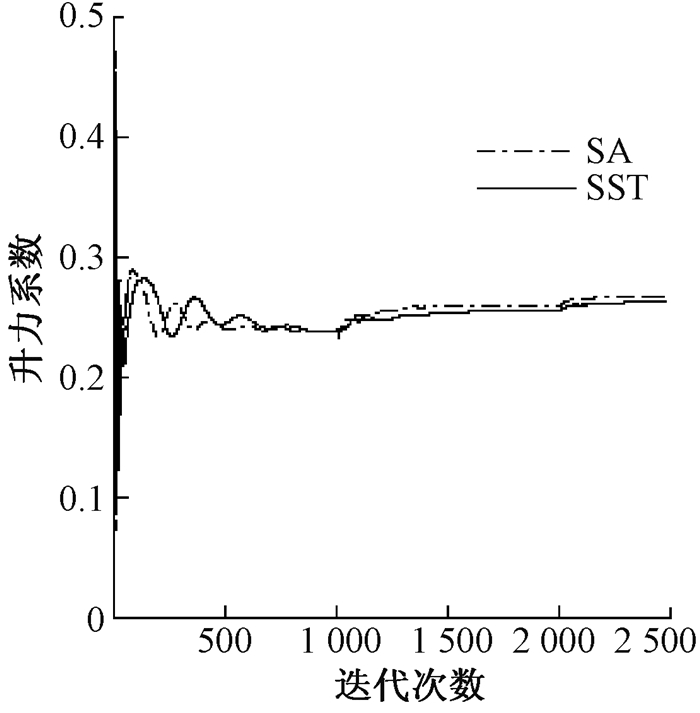
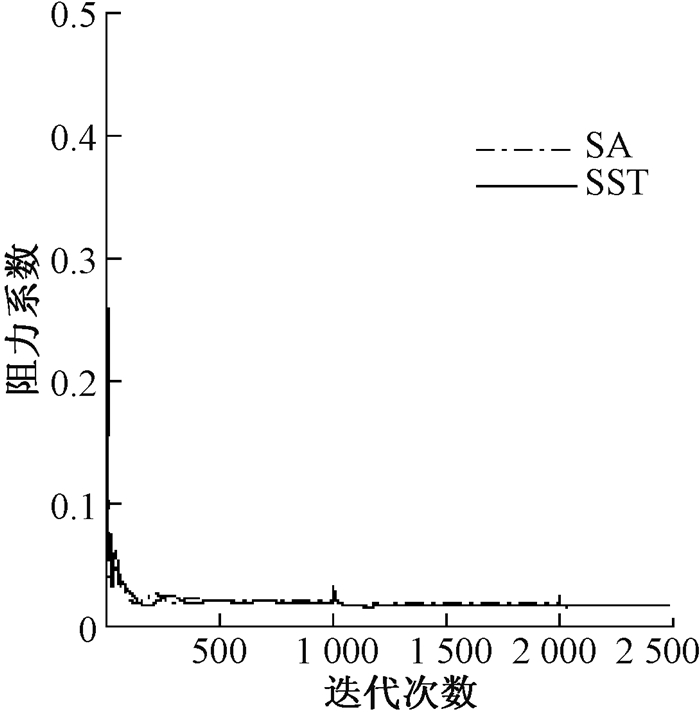
图 4~6分别是SA模型和SST模型下的残值、升力、阻力系数收敛史的比较.从图 4可看出, SA模型在2 500步左右基本达到稳定状态, 收敛误差约为10-9; SST模型在4 000步左右基本趋于稳定, 收敛误差约为10-10, 即SA模型表现出高的收敛速度, SST模型具有较高的计算精度.从图 5和6可以看出, 两种模型下的升力系数、阻力系数迭代到1 500步左右时几乎同时达到稳定状态, 但SST模型的稳定性稍高于SA模型.
|
图 4 残值收敛历程 Fig. 4 Course of the convergence of residual value |
|
图 5 升力系数收敛史 Fig. 5 History of the convergence of lift coefficients |
|
图 6 阻力系数收敛史 Fig. 6 History of the convergence of drag coefficients |
在统计分析的基础上通过比较变异系数的大小, 判断气动力特性受湍流模型的影响程度, 即变异系数越大影响就越大, 反之则小.表 1给出了升力系数、阻力系数及黏性阻力系数在两种湍流模型下的计算结果和其他方法下的计算结果[2, 11].从表 1可得出:黏性阻力系数的变异系数最大, 升力系数的变异系数最小; 两种湍流模型的升力、阻力、黏性阻力系数与其他计算结果相比较, SA模型的误差分别为0.001 55、0.000 11、0.000 02;SST模型的误差分别为0.002 79、0.000 95、0.004 522.表 1不仅表明升力系数受湍流模型的影响没有阻力系数大, 且验证了本文的计算结果是较好的, 特别是SA模型表现出的气动力特性要略好一些.
|
|
表 1 两种湍流模型对气动力的影响及与其他计算结果的比较 Tab. 1 The influence of two turbulence models on aerodynamic force and comparison with other computational results |
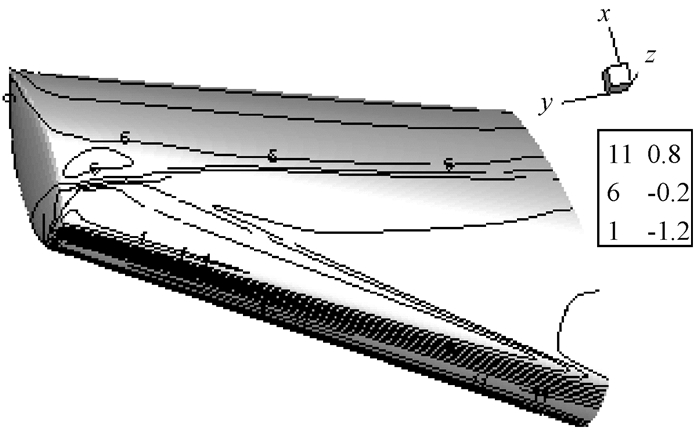
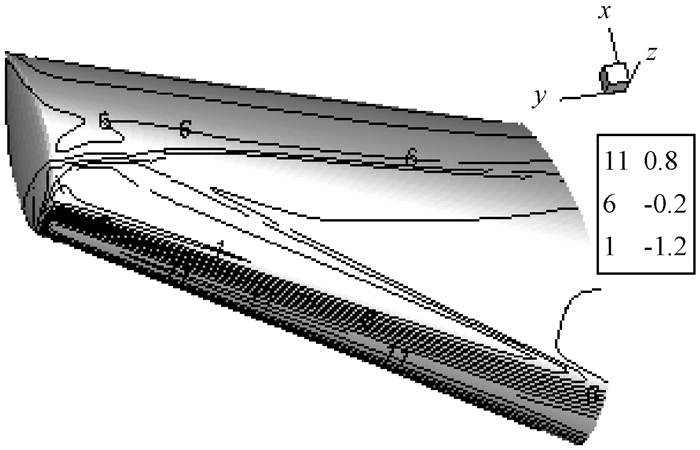
如图 7和8所示, M6机翼在SA、SST模型下的上表面等压力线差异较小; M6机翼上表面翼根的两道激波到翼稍处逐渐汇合, SA、SST模型预测到的λ型激波结构与实验结果几乎一致.由M6机翼在SA、SST模型下3个典型展向处的等马赫线对比, 可知M6机翼表面的马赫数沿着翼展方向增大幅度逐渐减小; 在展向y/b分别为0.20、0.65处有两道激波, 并在展向y/b为0.80处逐渐汇合; SST模型预测到的激波变化过程略好于SA模型预测到的激波变化过程; 与图 3中两种湍流模型下的压力系数分布的激波变化一致.由此可得, SA模型对激波的模拟能力没有SST模型的好, SST模型能更精确地模拟激波和接触激波.
|
图 7 SA模型下M6机翼上表面等压力线 Fig. 7 The pressure line on the upper surface of the M6 under SA model |
|
图 8 SST模型下M6机翼上表面等压力线 Fig. 8 SST model under the M6 wing upper surface pressure line |
本文通过求解NS方程, 分别耦合SA、SST模型的全湍流数值模拟结果, 与实验结果进行对比、分析, 得出以下结论.
1) 与实验数据相比, 两种湍流模型预测的机翼表面压力系数分布结果很好, 从而验证了求解技术及计算程序的可行性.
2) SA模型的收敛速度和计算效率略高于SST模型, 但SST模型的计算精度和稳定性略高于SA模型.
3) 湍流模型对阻力特别是黏性阻力的影响最大, 升力受湍流模型的影响没有阻力的大, SA模型表现出的气动力特性要略好一些.
4) 相对于SA模型来说, SST模型对激波的模拟能力较强, 精度较高.
| [1] |
朱自强. 应用计算流体力学[M]. 北京: 北京航空航天大学出版社, 1998.
(  0) 0) |
| [2] |
郑秋亚.基于Navier-Stokes方程的复杂流动数值模拟精度与并行计算研究[D].西安: 西安电子科技大学, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1958785
(  0) 0) |
| [3] |
ROE P L. Approximate riemann solvers, parameter vectors, and difference schemes[J]. Journal of computational physics, 1981, 43: 357-372. DOI:10.1016/0021-9991(81)90128-5 (  0) 0) |
| [4] |
涂国华, 燕振国, 赵晓慧, 等. SA和SST湍流模型对高超声速边界层强制转捩的适应性[J]. 航空学报, 2015, 36(5): 1471-1479. (  0) 0) |
| [5] |
SPALART P, ALLMARAS S. An one-equation turbulent model for aerodynamic flows[C]//30th Aerospace Sciences Meeting and Exhibit. Reno, NV, 1992: 439. http://www.researchgate.net/publication/236888804_A_One-Equation_Turbulence_Model_for_Aerodynamic_Flows
(  0) 0) |
| [6] |
MENTER F, RUMSEY L. Assessment of two-equation turbulent models for transonic flows[C]//Fluid Dynamics Conference 1994. Colorado Springs, CO, 1994: 2326. https://arc.aiaa.org/doi/abs/10.2514/6.1994-2343
(  0) 0) |
| [7] |
石磊, 杨云军, 周伟江. 两种湍流模型在高速旋转翼身组合弹箭中的对比研究[J]. 力学学报, 2017, 49(1): 85-92. (  0) 0) |
| [8] |
刘景源. SST湍流模型在高超声速绕流中的改进[J]. 航空学报, 2012, 33(12): 2192-2201. (  0) 0) |
| [9] |
韩涛. 湍流模型在民机跨声速绕流计算的应用研究[J]. 航空计算技术, 2013, 43(3): 77-79. (  0) 0) |
| [10] |
唐雨萌, 柳阳威, 陆利蓬. 高升力翼型复杂流动模拟型性能评估[J]. 航空动力学报, 2016, 31(12): 2860-2869. (  0) 0) |
| [11] |
尹翔, 冯金福, 张俊祥. 一种典型翼型在湍流模型中的数值仿真分析[J]. 计算机仿真, 2013, 30(4): 116-141. DOI:10.3969/j.issn.1006-9348.2013.04.027 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


