产品表面缺陷检测是检测工业产品是否满足质量要求的主要手段.随着工业自动化的快速发展,传统的人工表面检测已经不能满足现代工业快速、稳定、可靠的要求.而机器视觉技术[1-2]具有高度自动化、稳定性好、无损检测等优势,很好地满足了工业生产中批量大、精度高的需求.因此,在现代表面检测领域得到了广泛的应用[3-6].
目前,国内外很多学者针对表面缺陷检测进行了大量的研究[7-10].文献[7]提出了基于Sobel与分数阶微分的边缘检测算法,对圣女果表面进行缺陷检测.文献[8]通过处理数字颜色信号来判断金属表面缺陷的检测.文献[9]通过对圆柱型零件进行旋转拍摄来实现了缺陷的检测.文献[10]采用“实时浓妆补正技术”对轴承钢珠表面的缺陷进行检测.在这些研究中,对物体表面缺陷的检测,都有针对性和局限性.边缘检测算法不适用于表面粗糙的目标体,处理数字颜色信号的方法对金属缺陷的检测只适用于特定的反光材料,通过旋转拍摄很难检测到复杂纹理的缺陷,“实时浓妆补正技术”只针对特定的金属进行检测.因此,本文对微小圆柱端面检测提出了一种新的测量方法,即通过基于双光栅型结构光交叉打光的方式[11-12],提取物体表面特征信息,滤除复杂的图像背景,建立高斯混合模型[13-14](Gaussian mixture model, GMM),对交叉点特征进行分类,从而得到端面的形状特征,实现对缺陷区域的提取和检测.
1 系统组成缺陷检测系统[15]主要由图像采集、图像处理与判断两部分组成.图像采集通常包含相机、镜头、光源及计算机等,根据不同接口类型相机,可选择是否采用图像采集卡.采集到的图像经计算机算法处理后,判断被检测物的缺陷状态.然后,根据工业标准对元件进行分选.
2 图像采集与特征提取 2.1 图像采集图像采集是整个机器视觉检测的基础,获取高质量的图像对后续处理十分重要.本文检测的元件对象为包含中心孔的微小圆柱端面,其中心孔直径大约1.6 mm,圆柱直径大约5.5 mm,本底颜色为灰黑色.采用通常的打光成像方法,比如平行光、环形光,获取的图像背景复杂,很难从中提取到物体表面特征信息.而采用结构光打光模式,可以滤除复杂背景,将表面特征显著呈现.
本文采用的光栅型结构光,可以产生单光条宽50 μm、光条间距200 μm的超细平行光束,其投射到检测物体表面,光条纹形状会随着圆柱端面形状变化而发生扭曲变形,通过测量光条纹的扭曲变形程度,可反推圆柱端面形状特征.经过模型计算与实验表明,条纹扭曲变形程度也取决于结构光条纹与缺陷边缘的相对走向.结构光对走向垂直于光条纹的缺陷边缘反应较为敏感,而当缺陷边缘与结构光条纹走向相同时,光条纹形状变化较小.因此,本文采用2组结构光从两侧对称打光,两个方向的条纹夹角为90°,可以将各种走向的缺陷全部突显出来.图 1(a)为平行光下的图像,图 1(b)、图 1(c)分别为左右结构光各自打光时的图像.具体图像采集结构图如图 2所示.

|
图 1 打光成像模式对比 Fig. 1 Comparison of light imaging mode |
|
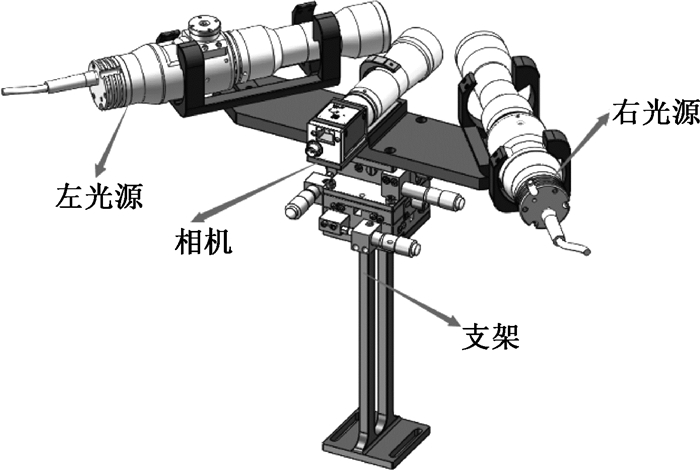
图 2 采集系统结构图 Fig. 2 Acquisition structure system |
对微小圆柱端面的缺陷检测,需要提取出有效的感兴趣区域,剔除其他干扰.首先,对2幅图像进行叠加、阈值后进行闭运算,可得到微小圆柱的中心孔,然后通过微小圆柱中心向外确定外直径,得到其所需的圆形感兴趣区域.接下来,提取感兴趣区当中的光条纹及交叉点.整个过程如图 3所示.交叉点的特征很大程度反映了光栅条纹的扭曲程度,因此,可以通过对交叉点特征的分类和条纹本身形态变化的分析,判断圆柱端面缺陷区域.

|
图 3 交叉点提取过程 Fig. 3 Crosspoint-extraction processing |
采用高斯混合模型对感兴趣区域内交叉点进行分类,其困难在于特征参数的选取.本文提取以下5个特征来建立高斯混合模型.
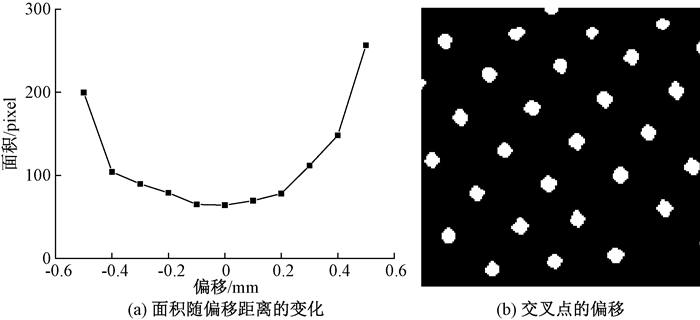
1) 交叉点面积.交叉点面积大小随着端面高低起伏而变化,与点到焦平面的距离成近似正比关系,如图 4(a)所示,横坐标零点为焦平面所在位置.2)交叉点最小外接椭圆长轴Ra.缺陷边缘和斜面上的交叉点一般呈椭圆状,有较大的Ra值.3)交叉点所属条纹宽度特征,它可以增加缺陷区域判定的置信度.4)交叉点所属条纹左偏移特征. 5)交叉点所属条纹右偏移特征.正常区域图像条纹之间的距离为固定值,而缺陷区域条纹之间则会发生偏移,交叉点排列发生错乱,如图 4(b)所示.求交叉点与离它最近的左结构光条的距离,作为左偏移特征.求交叉点与离它最近的右结构光条的距离,作为右偏移特征.
|
图 4 特征的选择 Fig. 4 Feature selection |
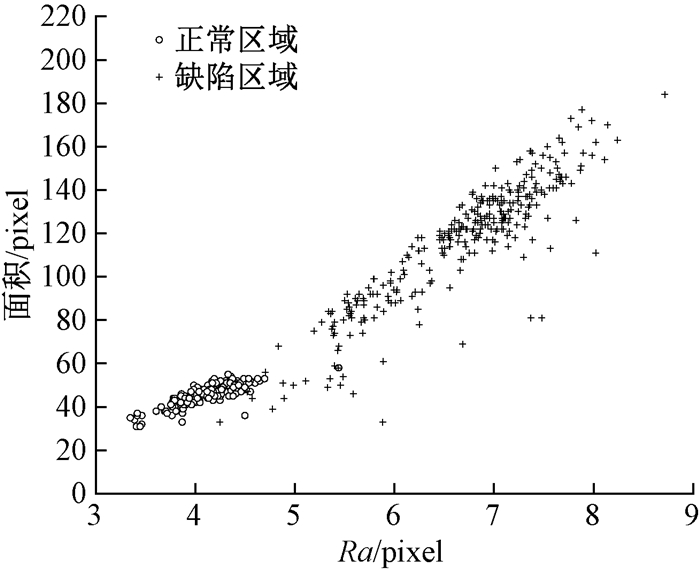
人工随机提取300个完好区域与300个缺陷区域的特征值,对其数据的分布进行分析,结果如图 5所示.其中,横坐标为交叉点椭圆长轴Ra,纵坐标为交叉点面积A.从图 5可以看出,正常区域与缺陷区域的分布特征区分显著.
|
图 5 特征分布 Fig. 5 Characteristic distribution |
高斯混合模型是用若干个高斯概率密度函数来拟合各种事物分布的模型,也被视为一种聚类的方法.利用其高鲁棒性的特点进行交叉点的分类,其概率密度函数为
| $ p(\boldsymbol{x} | \boldsymbol{\mu}, \boldsymbol{\Sigma}, \boldsymbol{\pi})=\sum\limits_{k=1}^{K} \boldsymbol{\pi}_{k} N\left(\boldsymbol{x} | \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}\right), $ | (1) |
其中:N(x|μk, Σk)为n维高斯函数,与x的维度保持一致,维度即特征数量,本文为5.
| $ N\left( {\mathit{\boldsymbol{x}}|{\mathit{\boldsymbol{\mu }}_k}, {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k}} \right) = \frac{1}{{{{(2\mathit{\boldsymbol{\pi }})}^{\frac{n}{2}}}\det {{(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})}^{\frac{1}{2}}}}}\exp \left\{ { - \frac{1}{2}{{(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\mu }})}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{ - 1}}(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\mu }})} \right\}, $ | (2) |
其中:x为某个样本;K表示高斯混合模型中包含K个高斯分布;μk表示第K个高斯分布的均值;Σk表示第K个高斯分布的协方差矩阵;π是权重因子;第K个分布的权重为πk,πk>0,且
通常使用最大期望(expectation maximization,EM)算法来求解高斯混合模型,EM算法是一种迭代求解期望最大值的算法.求解前需预设初始化参数θ0=[π0, μ0, Σ0].本文使用高斯混合模型对交叉点进行分类,包含2个高斯分布,即K为2类(完好区域点和缺陷区域点).引入隐变量z,其纬度与K保持一致.zk∈{0, 1},且
| $ P(z) = p\left( {{z_1}} \right)p\left( {{z_2}} \right) \cdots p\left( {{z_k}} \right) = \prod\limits_{k = 1}^K {\pi _k^{{z_k}}} , $ | (3) |
其中:z中只有一个zk为1,另一个为零.所以zk=1的概率为πk.
EM算法一般共分为两步求解.第一步,根据贝叶斯准则,用上一次迭代后的参数(第一次为初始参数)计算后验概率p(z|x).
| $ {\gamma _{ik}} = p\left( {{z_k} = 1|{x_i}} \right) = \left( {{\pi _k}N\left( {{x_i}|{\mathit{\boldsymbol{\mu }}_k}, {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k}} \right)} \right)/\left( {\sum\limits_{j = 1}^K {{\pi _j}} N\left( {{x_i}|{\mathit{\boldsymbol{\mu }}_j}, {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_j}} \right)} \right). $ | (4) |
第二步,使用第一步的后验概率最大化似然函数,重新估计参数的值,其中N为样本数.求解各个参数的最大化似然函数得到
| $ {\pi _k} = \sum\limits_{i = 1}^N {{\gamma _{ik}}} /N, {\mathit{\boldsymbol{\mu }}_k} = \left( {\sum\limits_{i = 1}^N {{\gamma _{ik}}} {x_i}} \right)/\\ \left( {\sum\limits_{i = 1}^N {{\gamma _{ik}}} } \right), {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k} = \left( {\sum\limits_{i = 1}^N {{\gamma _{ik}}} \left( {{x_i} - {\mathit{\boldsymbol{\mu }}_i}} \right){{\left( {{x_i} - {\mathit{\boldsymbol{\mu }}_i}} \right)}^{\rm{T}}}} \right)/\left( {\sum\limits_{i = 1}^N {{\gamma _{ik}}} } \right). $ |
然后将第二步重新得到的参数代入第一步进行循环,直到算法收敛.求解最大似然函数时,由于小于1的概率连乘后得到较小的值,一般对似然函数取log.收敛条件为达到最大迭代次数或者最大似然函数值,两次迭代的差值小于预设值.
3.3 交叉点的筛选根据2.2提取图像交叉点的特征,代入3.2训练后的高斯混合模型,比较2个类的概率大小,选取概率大的类作为此交叉点的分类结果.由于缺陷部分可能丢失交叉点信息,因此,统计正常交叉点个数,与微小元件内外直径做对比,得到缺陷比例.
4 实验结果分析为了验证高斯混合模型对微小圆柱元件缺陷检测的准确性和稳定性,随机选择100个微小圆柱进行测试,包含25个缺陷圆柱和75个正常圆柱,对单个圆柱重复测量5次.高斯混合模型对5次分类后的结果如表 1所示.其中,部分缺陷圆柱的缺陷比例经过河南省计量院的精确计量,误差小于1%,计量缺陷圆柱的重复测量结果如表 2所示.根据需求,缺陷比例小于10%的为完好圆柱,大于等于10%的为缺陷圆柱.则缺陷检出率R和算法总识别率V为R=R0/N0, V=V0/N,其中:R0为正确检出缺陷圆柱的数量;N0为缺陷圆柱的总数量;V0为正确检测圆柱的数量;N为检测圆柱的总数量.
|
|
表 1 分类结果 Tab. 1 Classification result |
|
|
表 2 重复测量结果 Tab. 2 Multiple results |
实验结果表明,高斯混合模型对微小圆柱元件端面的缺陷分类效果较好,缺陷检出率达96.8%,重复测量结果在计量值的4%以内波动,验证了本文方法的可行性和稳定性,其中内外边缘出现的倒角可能会对结果造成一定的影响.使用训练后的高斯模型进行检测,每个微小圆柱端面判断的时间不超过0.4 s,满足工业生产的要求.图 6为随机选择的缺陷分类结果图.

|
图 6 提取结果 Fig. 6 Extraction result |
引入文献[11]中的三角剖分算法,对5次采集的元件图像进行测量.在时间、缺陷检出率和总识别率上作了对比:本文算法与文献[11]的算法所用时间分别为0.38 s和1.20 s;缺陷检出率分别为96.8%和68.8%;算法识别率分别为99.2%和87.2%.本文提出的方法针对微小圆柱元件在时间上仅为三角剖分算法的1/3,并且缺陷检出率有明显优势,表明了本文方法的可靠性和实用性.
5 结束语本文采用双光栅型结构光交叉打光的方式,将元件端面的形态变化通过光条的扭曲反映出来.通过图像处理技术,将光条的形态变化提取转化成对交叉点的处理,大幅度降低了图像处理的复杂度.通过高斯混合模型对交叉点形态特征及条纹宽度、偏移特征进行分类组合,实现了复杂背景下微小圆柱元件端面缺陷快速、准确的测量.实验结果表明,本文设计的方法测量稳定,缺陷检出率可达96.8%,同时测量时间不大于0.4 s,满足工业自动化检测的要求.
| [1] |
李涛涛, 杨峰, 许献磊. 基于多视觉线结构光传感器的大尺度测量方法[J]. 中国激光, 2017, 44(11): 1104003. (  0) 0) |
| [2] |
SHIM J H, NAM T H. Machine vision based automatic measurement algorithm of concentricity for large size mechanical parts[J]. Journal of physics: conference series, 2017, 806: 012002. DOI:10.1088/1742-6596/806/1/012002 (  0) 0) |
| [3] |
李慧娴.基于图像处理的微小元件端面裂纹及缺陷检测算法的研究[D].郑州: 郑州大学, 2018.
(  0) 0) |
| [4] |
刘丹.基于机器视觉的微小圆柱元件端面缺陷检测方法的研究[D].郑州: 郑州大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10459-1018107900.htm
(  0) 0) |
| [5] |
ALEIXOS N, BLASCO J, NAVARRÓN F, et al. Multispectral inspection of citrus in real-time using machine vision and digital signal processors[J]. Computers and electronics in agriculture, 2002, 33(2): 121-137. (  0) 0) |
| [6] |
吴思远, 张召, 邹洋. 基于2D Gabor小波和HSV空间的木材缺陷检测[J]. 郑州大学学报(理学版), 2010, 42(1): 93-97. (  0) 0) |
| [7] |
杜永忠, 平雪良, 何佳唯. 圣女果表面缺陷检测与分级系统研究[J]. 农业机械学报, 2013, 44(S1): 194-199. (  0) 0) |
| [8] |
LEE S, CHANG L M, SKIBNIEWSKI M. Automated recognition of surface defects using digital color image processing[J]. Automation in construction, 2006, 15(4): 540-549. DOI:10.1016/j.autcon.2005.08.001 (  0) 0) |
| [9] |
苏俊宏, 刘胜利. 圆柱型高精密零件表面缺陷检测及形貌分析[J]. 激光与光电子学进展, 2014, 51(4): 041202. (  0) 0) |
| [10] |
陈青云. 基恩士视觉产品手册[M]. 上海: 基恩士国际贸易(上海)有限公司, 2013: 628-633.
(  0) 0) |
| [11] |
马晨.基于结构光的三维形貌视觉测量方法研究[D].西安: 西安理工大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10700-1018835214.htm
(  0) 0) |
| [12] |
朱禄.基于线结构光的三维测量系统研究[D].广州: 广东工业大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-11845-1018865501.htm
(  0) 0) |
| [13] |
麻妙玲, 戴敏, 孟丹阳, 等. 基于高斯混合模型的标准心电波形筛选[J]. 天津理工大学学报, 2018, 34(5): 20-24. DOI:10.3969/j.issn.1673-095X.2018.05.005 (  0) 0) |
| [14] |
李新会, 罗红元, 徐晓琴, 等. 基于主成分分析和高斯混合模型的茶叶分类研究[J]. 郑州大学学报(理学版), 2015, 47(4): 62-65. DOI:10.3969/j.issn.1671-6841.2015.04.012 (  0) 0) |
| [15] |
赵海峰, 郭燕, 崔吉, 等. 基于机器视觉的小微零件缺陷检测技术及装置研究[J]. 工具技术, 2018, 52(11): 147-149. DOI:10.3969/j.issn.1000-7008.2018.11.048 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


