2. 郑州大学 化学与分子工程学院 河南 郑州 450001
2. College of Chemistry and Molecular Engineering, Zhengzhou University, Zhengzhou 450001, China
工业4.0是将设备和生产流程进行联网的第四次工业革命,实现从基础原料到终端产品在一套完整的生产线上连续生产,充分体现了高效率、节能环保、降低人力和物力成本等优点[1-2].塑料加工业实现工业4.0的重点在于生产效率、灵活性、自动化、适用性和产品质量的全面改善,为塑料加工企业带来巨大的发展机遇,对原料综合性能的要求不断提高.
尼龙,特别是尼龙66是一种重要的工程塑料,在国民生产中占据重要的位置.快速成型尼龙66是一种能满足工业4.0要求的新材料,但在加工过程中必然要经历非等温过程.因此,研究快速成型尼龙66在非等温条件下的结晶动力学具有直接而现实的意义.
非等温结晶动力学过程非常复杂,目前理论及数据处理方法已有十余种,如Ziabicki方程、Avrami方程、Jeziomy方程、Ozawa方程、Mandelkern方程、Patel方程和Mo Zhishen方程等,但仍无一种令人满意的方法[3-8].本文采用DSC方法,并借助Jeziomy方程、Ozawa方程和Mo Zhishen方程对快速成型尼龙66的非等温结晶动力学行为进行分析,为尼龙66在工程塑料领域的应用开发提供理论支持.
1 实验部分 1.1 原料快速成型尼龙66(RP PA66)切片由宁波七诺新材料科技有限公司提供.
1.2 仪器与测试方法测试仪器是美国TA Instruments生产的差示扫描量热仪(DSC Q20).
DSC测试步骤如下:称取8~10 mg快速成型尼龙66切片放置在专用DSC坩埚中,以标准空坩埚作为对比样,在高纯氮气的保护下以10 ℃/min的速率升温至280 ℃,保持5 min以消除热历史,然后以2、5、10、15、20、50 ℃/min的速率降温至30 ℃,记录这个阶段的热流-时间-温度曲线,得到一系列不同降温速率的非等温结晶DSC结晶曲线.
2 结果与讨论 2.1 非等温结晶过程与小分子结晶相比较,聚合物结晶过程在结晶机理、结晶动力学和结晶热力学等方面都具有特殊性.聚合物结晶过程是链段松弛过程,需要一定时间完成结晶过程,表现为结晶过程滞后于降温过程.降温速率越快,滞后期越明显,结晶峰位置随降温速率的增加而移向低温区.
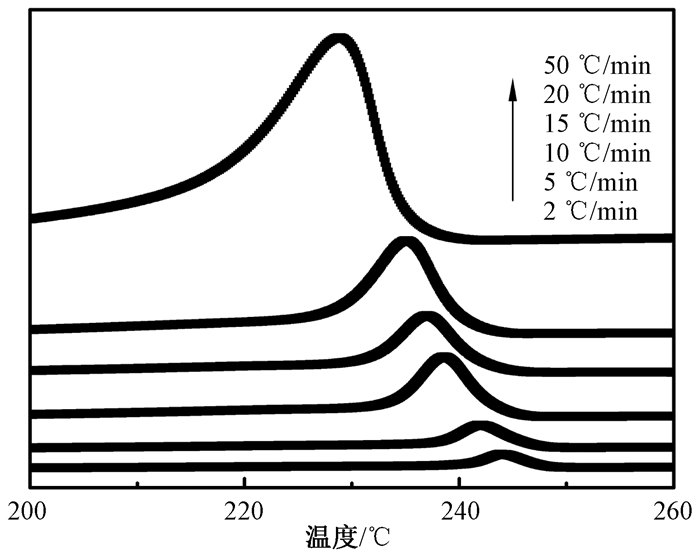
图 1为快速成型尼龙66在不同降温速率条件下的DSC曲线.可以看出,对于快速成型尼龙66而言,随着降温速率增加,结晶峰的温度范围变宽.这是因为降温速率大时,结晶时间缩短,聚合物链段没有足够的时间进行迁移、取向和重排堆砌;在相同的时间区间内,聚合物经历的温度区间变大,所以结晶峰温度变宽.
|
图 1 快速成型尼龙66在不同降温速率条件下的DSC曲线 Figure 1 The DSC plots of RP PA66 with different cooling rates |
结晶峰值温度对应于结晶速度达到最大时的温度.表 1列出了快速成型尼龙66降温结晶过程中的热力学参数.可以看出,结晶起始温度和结晶峰值温度随着降温速率的增加而下降,而过冷度随之增加,进一步证明降温速率越大,结晶滞后现象越明显.同时,随着降温速率的增加,结晶起始到结晶速率最大的时间(峰值结晶时间)变短.半结晶时间越短,说明快速成型尼龙66的结晶速率随降温速率的增加而增加.
|
|
表 1 快速成型尼龙66降温结晶过程中的热力学参数 Table 1 The thermodynamic parameters of RP PA66 in cooling crystallization process |
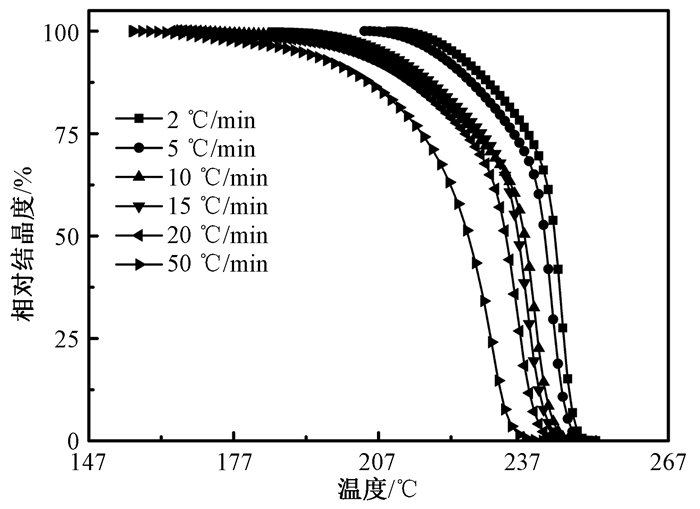
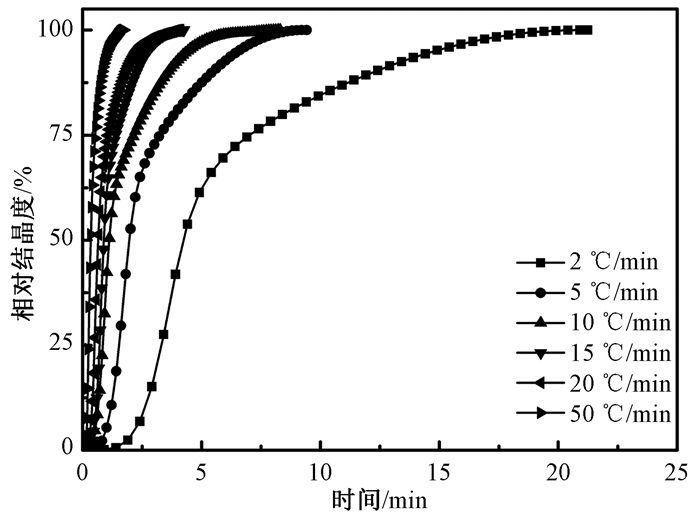
图 2和图 3分别为快速成型尼龙66的相对结晶度随温度和时间的变化关系图.快速成型尼龙66的结晶过程分为诱导期、主结晶期和后结晶期3个阶段.图 2和图 3表明,在诱导期,熔体温度高,链段运动能力强,生成的取向结构或晶体易被破坏;而在低温区,链段运动能力下降,生成的取向结构趋向稳定,有利于促使链段在成核剂周围聚集并生长成为晶体.体系停留在高温区的时间随着降温速率的增加而减少,相应地,诱导期时间随着降温速率的增加而减少.此外,当快速成型尼龙66的相对结晶度比较低时,相对结晶度随结晶时间增加或温度降低而迅速增加;当快速成型尼龙66的相对结晶度增大到一定程度时,晶体之间相互膨胀与挤压,出现次结晶现象,根据降温速率的不同,转变点发生在相对结晶度为75%±10%区间.由图 2可见,次结晶温度跨度大于主结晶期.这是因为在结晶后期,生成的晶体互相碰撞、挤压导致晶体生长速率下降,同时体系中自由链段越来越少,温度下降导致链段运动能力降低所致.
|
图 2 快速成型尼龙66的相对结晶度与结晶温度之间的关系 Figure 2 The relationship between the relative crystallinity and crystallization temperature of RP PA66 |
|
图 3 快速成型尼龙66的相对结晶度与结晶时间之间的关系 Figure 3 The relationship between the relative crystallinity and crystallization time of RP PA66 |
与等温结晶过程不同,聚合物的非等温结晶过程受温度、时间、冷却速率等多维度因素的影响,目前还没有一种广为接受的方法来分析非等温结晶过程.绝大多数的聚合物加工都是在非等温条件下进行的,研究非等温结晶过程对聚合物的应用开发具有非常重要的实践意义.
2.2.1 Jeziomy法Jeziomy方程是在Avrami方程基础上演变而来的.Avrami方程是相对结晶度与结晶时间的双对数关系式,只适合描述聚合物结晶的初期过程,其作为一个分析聚合物结晶动力学的理论,尽管相关参数的物理意义尚不明确,但在比较分析时仍有一定的指导意义.
Avrami方程为
| $ \log \left[{-\ln \left( {1-{X_t}} \right)} \right] = \log \;{Z_t} + n\log \;t, $ |
Jeziomy方程为
| $ \log \left[{-\ln \left( {1-{X_t}} \right)} \right] = \log \;{Z_c} + n\log \;t, $ |
式中:Xt为温度t时的相对结晶度;Z为结晶速率常数;n为Avrami指数.Jeziomy方程考虑了降温速率Φ的影响,两个方程之间的关系在于:log Zc=log Zt/Φ.
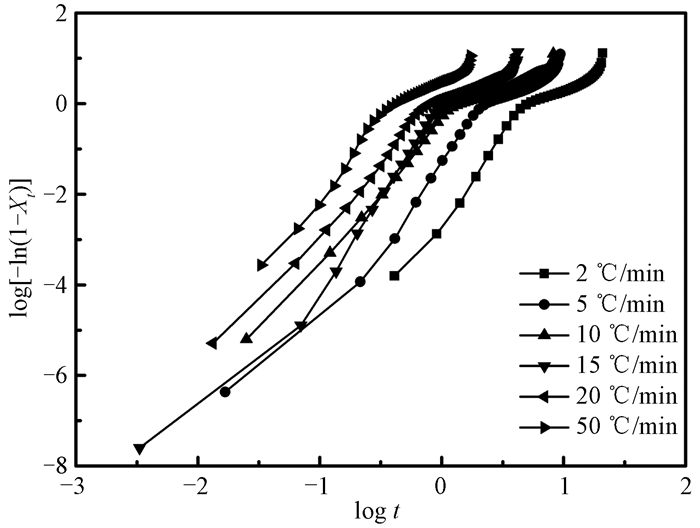
图 4是快速成型尼龙66的log[-ln(1-Xt)]~log t关系图,两者之间并不存在线性关系,对接近线性部分分别进行拟合,相应的结晶动力学参数列于表 2中.可以看出,在主结晶期,Avrami指数n是一个接近于3的常数,表明快速成型尼龙66的结晶按三维球晶方式生长;但-log Zt和-log Zc表现为先减小而后增大的趋势,表明快速成型尼龙66的结晶过程具有复杂性.
|
图 4 快速成型尼龙66的log[-ln(1-Xt)]和log t关系图 Figure 4 Plots of log[-ln(1-Xt)] versus log t for RP PA66 |
|
|
表 2 基于Jeziomy方程的非等温结晶过程的动力学参数 Table 2 The dynamic parameters of the non-isothermal crystallization process based on Jeziomy equation |
在后结晶期,快速成型尼龙66的Avrami指数n基本随着降温速率的增加而缓慢增加,这与降温速率增加,样品冷却速率随之增加,链段运动能力下降,生成的晶体缺陷随着降温速率的增加而增多,在后结晶期不完善晶体趋向稳定和未结晶部分继续结晶有关.
鉴于快速成型尼龙66的log[-ln(1-Xt)]与log t之间并不存在线性关系,并且对线性区间进行拟合,所获得的Avrami指数n和结晶动力学参数并不趋于常数,且二者的变化趋势步调并不一致.因此,Jeziomy方程不适合描述快速成型尼龙66的结晶过程.
2.2.2 Ozawa法Ozawa方程是基于Evans理论,从聚合物结晶的成核和生长出发而推导出的等速变温时的结晶动力学方程.
Ozawa方程为
| $ \log \left[{-\ln \left( {1-{C_T}} \right)} \right] = \log \;K\left( T \right) -m\log \;\mathit{\Phi }, $ |
式中:CT为温度T时的相对结晶度;Φ为升温或降温速率;m为Ozawa指数;K(T)与成核方式、成核速率、晶核的生长速率等因素有关,是温度的函数,在等速降温结晶过程中成为冷却函数.
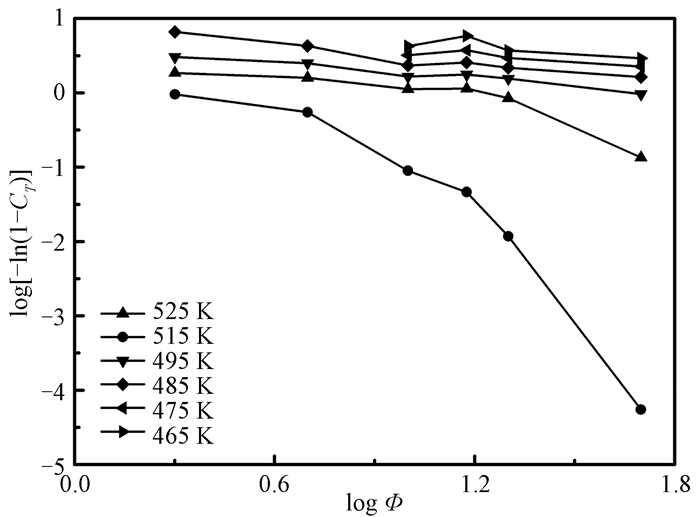
图 5是快速成型尼龙66的log[-ln(1-CT)]~log Φ关系图,从图中各曲线的变化趋势可见,在有效的实验区间内,log[-ln(1-CT)]与log Φ之间并不存在线性关系.因此,Ozawa方程不适合描述快速成型尼龙66的结晶过程.
|
图 5 快速成型尼龙66的log[-ln(1-CT)]和log Φ关系图 Figure 5 Plots of log [-ln(1-CT)] versus log Φ for RP PA66 |
莫志深教授在Avrami方程和Ozawa方程的基础上,将两个方程结合在一起,使降温速率Φ和结晶时间t之间存在关系.
Mo Zhishen方程为
| $ \log \;\mathit{\Phi }{\rm{ = log}}\;F\left( T \right)-a\log \;t, $ |
式中:F(T)为某一体系在单位时间内达到某一相对结晶度时必须选取的冷却(或加热)的速率值,可作为表征聚合物结晶快慢的参数; a=n/m, 其中n为表观Avrami指数,m为Ozawa指数.
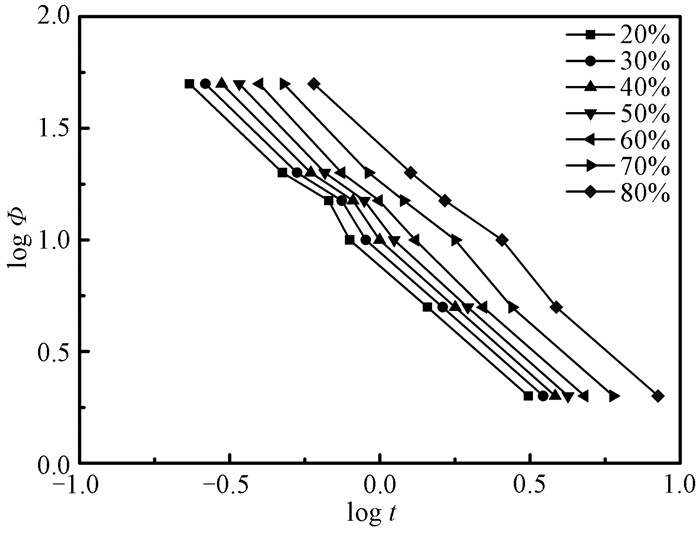
图 6是快速成型尼龙66的log Φ和log t关系图.可以看出,在比较低的相对结晶度时,log Φ与log t之间存在良好的线性关系,随着相对结晶度的增加,二者之间的线性关系逐渐变差,表明在主结晶期Mo Zhishen方程适用于描述快速成型尼龙66的结晶行为.
|
图 6 快速成型尼龙66的log Φ和log t关系图 Figure 6 Plots of log Φ versus log t for RP PA66 |
相应的结晶动力学参数列于表 3中.从表中数据可以看出,a值是一个居于1.20~1.30之间的近似常数,而log F(T)值随着降温速率的增加而增加,表明在单位时间内,快速成型尼龙66要达到较高的相对结晶度,必须要选择较高的降温速率.
|
|
表 3 基于Mo Zhishen方程的非等温结晶过程的动力学参数 Table 3 The dynamic parameters of the non-isothermal crystallization process based on Mo Zhishen equation |
随着降温速率的增加,快速成型尼龙66的结晶峰移向低温区,并且峰宽增加,特别是在高速降温条件下,结晶峰的形状比纯粹尼龙66有了明显的改善;Jeziomy方程和Ozawa方程不适合描述快速成型尼龙66的结晶行为,而Mo Zhishen方程适用于描述快速成型尼龙66的结晶行为.提高降温速率有利于加快快速成型尼龙66的结晶速率.
| [1] |
李建广, 颜春, 李红周, 等. 尼龙6/石墨复合材料非等温结晶动力学研究[J]. 塑料工业, 2013, 41(1): 67-71. (  0) 0) |
| [2] |
张声春. 聚苯硫醚/尼龙6非等温结晶动力学的研究[J]. 现代塑料加工应用, 2007, 19(2): 37-39. (  0) 0) |
| [3] |
王劭妤, 赵欢敏, 石坚. 碳纳米管/尼龙6复合材料的非等温结晶动力学研究[J]. 塑料工业, 2012, 40(2): 71-74. (  0) 0) |
| [4] |
杨坡, 胡国胜, 王标兵. 尼龙6/11共聚物的非等温结晶动力学研究[J]. 中北大学学报(自然科学版), 2008, 29(2): 156-159. (  0) 0) |
| [5] |
张子勇, 林鹏英, 饶华新. 尼龙-64的非等温结晶动力学研究[J]. 材料导报, 2010, 24(6): 111-114. (  0) 0) |
| [6] |
张声春, 韩冰, 张春祥, 等. 半芳香共聚尼龙6T/6的非等温结晶动力学研究[J]. 塑料工业, 2013, 41(11): 91-94. DOI:10.3969/j.issn.1005-5770.2013.11.021 (  0) 0) |
| [7] |
付鹏, 杨韶辉, 曹凯凯, 等. 半芳香尼龙6T/66的合成和非等温结晶动力学的研究[J]. 高分子通报, 2010(1): 73-76. (  0) 0) |
| [8] |
林庆辉, 陈大俊. 有光和半消光尼龙6切片的非等温结晶动力学研究[J]. 合成纤维工业, 2015, 38(5): 21-25. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49

