2. 郑州大学第一附属医院 河南 郑州 450052
2. The First Affiliated Hospital of Zhengzhou University, Zhengzhou 450052, China
随着第二代高通量测序技术的发展,越来越多的生物数据可以方便快捷地供科研工作者使用。生物数据具有高维度、高噪声、样本量低且不同特征点之间关系复杂的普遍特征[1],如RNA表达量,其维度通常达到数万,相对而言样本量却极少, 这种现象在机器学习领域被称为“维数灾难”[2]。为了克服“维数灾难”,研究者做了大量的相关工作,例如利用传统机器学习的方法进行降维,减轻“维数灾难”对后续研究的影响[3-4]。但是由于生物数据相邻特征点联系紧密,某个特征点的异常可能导致不同程度的机体癌变,一般的降维算法无法有效提取其重要特征[5-7]。为了更直观地检测一维数据,同时降低对数据完整性的破坏程度,文献[8]提出利用希尔伯特曲线对股票走势进行维度转换的概念; 文献[9]利用希尔伯特曲线将随机生成的一维长向量映射为二维矩阵,并实现了数据的可视化。现有算法在进行肿瘤相关分析时通常只涉及一种数据,但生物体内部结构复杂,且肿瘤形成受多种因素的影响,故单一数据无法有效说明其成因[6]。本文提出基于融合数据的希尔伯特曲线-卷积神经网络(H-CNN)模型完成肿瘤类型的预测。首先对数据进行对数转化,去除缺失特征点, 然后根据染色体编号对每个样本的特征点进行重新排序,使相邻的特征点具有局部相似性,以便后续充分发挥CNN网络的性能; 重排序后使用变分自编码器将RNA表达量和DNA甲基化两种数据进行有效融合, 运用希尔伯特曲线完成融合数据一维到二维的映射; 将生成的二维数据送入CNN进行训练,利用训练好的模型对新样本进行分类,即对新样本进行肿瘤类型的预测。结果表明,基于融合数据的H-CNN模型在实验中表现出优异的性能。
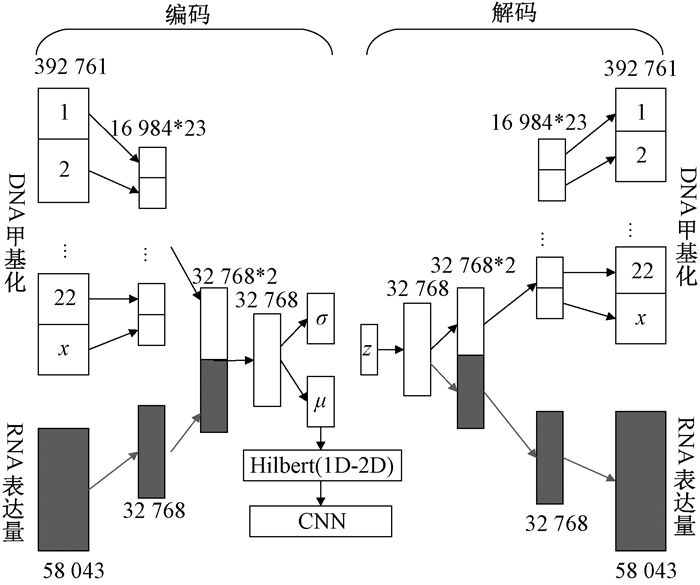
1 实验方法 1.1 网络结构网络结构流程如图 1所示,主要由变分自编码器(VAE)、希尔伯特曲线和卷积神经网络三个部分组成。
|
图 1 网络结构流程 Fig. 1 Network structure process |
在进行肿瘤类型预测、亚型分析、免疫治疗分析以及风险预测时,通常使用的数据有基因突变数据、RNA表达量数据、DNA甲基化数据、临床数据等。本文从TCGA数据库中获取19 683个肿瘤样本的RNA表达量和DNA甲基化数据,其中共包括32种肿瘤类型。
1.2.1 RNA表达量RNA是遗传信息在传递过程中的桥梁。RNA表达量原始样本形式为一维长向量,维度通常达到数万。RNA表达量的高低主要说明此时细胞分裂是否处于旺盛阶段:如果处于分裂旺盛状态,则RNA的表达量较高,否则RNA表达量较低。一般癌细胞生长周期短,其在生长阶段分裂始终处于旺盛状态,不同的癌变类型表现为RNA表达量不同程度的异常。
1.2.2 DNA甲基化DNA甲基化的数据形式与RNA表达量类似。DNA甲基化是DNA修饰途径之一,在甲基转移酶的催化下,DNA的CG两个核苷酸的胞嘧啶被选择性地添加甲基,形成5-甲基胞嘧啶。大量研究结果证实,某些基因出现高甲基化或者低甲基化都有可能导致不同类型肿瘤的形成[10]。
1.2.3 数据预处理数据预处理的目的主要是去除噪声和偏置信号。对于RNA表达量:去除位于Y染色体上的外显子(n=594),去除表达量为0的外显子(n=1 904),去除在所有样本中缺失率大于10%的外显子(n=248),最后保留的外显子的个数为58 043。对于DNA甲基化:去除无法匹配到人类参考基因组的探针(n=89 512),去除无法定位到染色体上的探针(n=2 545),去除位于Y染色体上的探针(n=346)以及缺失率大于10%的探针(n=414),最后保留的探针的个数为392 761。数据过滤之后,对两种数据进行对数转化。由于同一染色体上的特征点数值大小相近,故按照染色体编号对两种数据分别进行特征点的重新排序,使一维数据中的特征点具有局部相似性。
1.3 变分自编码器(VAE)VAE是一个强大的深度生成模型,能够从高维数据中学习到有意义的数据[11]。本文使用VAE对DNA甲基化和RNA表达量两种数据进行降维和重要特征提取,并将两种数据进行有效融合。假设输入数据为x={x1, x2, …, xn},VAE希望可以获得x的分布p(x), 从而得到x的值。VAE通过隐藏层z来计算x的分布,其实现方法为∫p(x|z)p(z)dz,其中p(x|z)可以表述为z生成x的过程。对于每一个样本x,认为其存在一个后验分布p(z|x),并假设其服从标准正态分布,需要通过编码器的不断学习拟合出来,在训练过程中达到μ无限接近0,σ2无限接近1。
为了使p(z|x)服从标准正态分布,使用相对熵(kl散度)对其进行优化,相对熵公式为kl(p(z|x)‖N(0, 1)),其值越小,表示两个概率分布越相似。最小化相对熵的过程可以表述为
| $ {L_{kl}} = \min (kl(p(z\mid x)\left\| N \right.(0, 1)))。$ | (1) |
式(1)经过计算可以变换为
| $ {L_{kl}} = \min \left( {\frac{1}{2}\sum\limits_{i = 1}^d {\left( {\mu _i^2 + \sigma _i^2 - \log \sigma _i^2 - 1} \right)} } \right), $ | (2) |
式中:d表示隐藏层维度; μi和σi2分别表示样本xi对应生成的p(zi|xi)所服从的正态分布的均值和方差。p(z|x)服从正态分布,z是从p(z|x)中采样而得,故z服从正态分布。为了对z进行采样,VAE采用重参数技巧,对z进行如下变换:
| $ z \sim N\left( {\mu , {\sigma ^2}} \right) \Rightarrow \left( {z - \mu } \right)/\sigma \sim \left( {0, 1} \right)。$ | (3) |
假设β服从标准正态分布,令(z-μ)/σ=β可得z=σβ+μ,取样β即可获得z。得到z的值后对输入数据进行重构,重构过程的目标函数可以表示为
| $ {L_{{\rm{VAE}}}} = \alpha {L_{lk}} + {E_{{\rm{VAE}}}}\left( {x, {x^\prime }} \right) + \gamma \cdot {\rm{ }}regularization, {\rm{ }} $ | (4) |
式中:α和γ分别为控制Llk和正则项的超参数。VAE模型优化过程就是通过最小化LVAE来实现的。EVAE(x, x′)表示x和x′之间的重构误差,可用式(5)误差或式(6)交叉熵分别表示为
| $ {E_{{\rm{VAE}}}}\left( {x, x'} \right) = \left\| {x - x'} \right\|, $ | (5) |
| $ E_{\mathrm{VAE}}\left(x, x^{\prime}\right)=-\sum\limits_{i=1}^{n}\left(x_{i} \log x_{i}^{\prime}+(1-x) \log \left(1-x_{i}\right)\right)。$ | (6) |
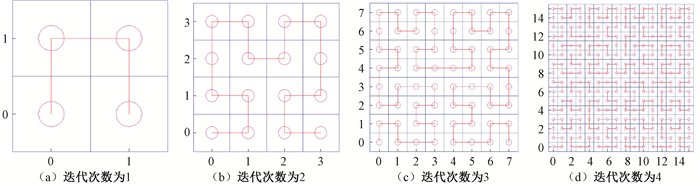
希尔伯特曲线的构造方法[9]为:当迭代次数为1时,把一个正方形分出4个相等的小正方形,然后从左下象限的小正方形开始至右下象限的小正方形结束,依次把小正方形的中心用线段连接起来; 当迭代次数为2时,把每个小正方形分成4个相等的更小的正方形,然后用上述方法把其中心连接起来,将这种操作方式无限进行下去,最终得到的极限情况的曲线就可以填满整个平面。结果表明,一维形式中相邻的特征点在二维形式中仍然处于相邻的位置,最大程度减小了对原始数据结构的破坏。图 2展示了迭代次数不同时希尔伯特曲线的制作过程。实验验证,通过希尔伯特曲线变换得到的二维图像中的某一点,即使迭代次数不同,其在图中所处的位置几乎不发生改变,随着迭代次数的增加,此点趋于一个固定的位置。这就意味着即使迭代次数发生改变,后续CNN网络不用重新训练,只需要对某些参数进行微调。
|
图 2 希尔伯特曲线的制作过程 Fig. 2 Making process of Hilbert curve |
对一维形式中的某一像素点进行追踪,发现其在不同迭代次数时所处的位置几乎不变。图 3给出了某一像素点在不同迭代次数时的位置。数据通过VAE融合后引入希尔伯特曲线,将19 683个肿瘤样本的融合数据从一维长向量映射为二维形式,不同的像素值布满二维空间。当迭代次数为8时,得到的图片分辨率为256*256。一维形式中的每个数值代表二维形式中的一个像素值,一维形式中的峰值对应二维形式中的阴影部分。峰值越高,对应颜色越深; 峰值所占的区间越大,二维形式中阴影部分对应的区域越大。

|
图 3 某一像素点在不同迭代次数时的位置 Fig. 3 The position of certain pixel at different iterations |
图 4和图 5分别为食道癌和结肠癌示例图。从图 4和图 5可以直观地看出,两者的差别主要集中在图的右侧中部。

|
图 4 食道癌示例图 Fig. 4 Schematic diagram of esophageal cancer |

|
图 5 结肠癌示例图 Fig. 5 Schematic diagram of colon cancer |
CNN主要由输入层、卷积层、激活层、池化层、全连接层、输出层组成[12]。其中,卷积层作为CNN的核心,通过局部感知和参数共享的方式达到降维和特征提取的目的; 激活层将前一层的输出通过非线性激活函数进行处理,用于模拟任意函数,增强网络的表征能力; 池化层可以降低数据的规模,增强CNN的泛化处理能力; 全连接层的作用相当于多层感知机,可以起到分类器的作用。本文在全连接层加入Dropout,Dropout可以通过阻止特征检测器的共同作用来提高神经网络的性能。前向传播时,让某个神经元以一定的概率停止工作,这样可以使模型泛化性更强。第一层卷积层包含64个卷积核,第二层和第三层卷积层分别包含128和256个卷积核。ReLU为本模型的激活函数,因为ReLU函数在随机梯度下降算法中收敛速度最快,而且不会出现梯度消失的问题。三个全连接层分别包含32 768、1 024、512个神经元,输出层个数为32,使用的CNN架构如图 6所示。

|
图 6 CNN架构 Fig. 6 CNN framework |
使用十折交叉验证的方法计算了准确率(A)、精确率(P)、召回率(R)、F1值等性能指标[13],计算公式为
| $ A = \frac{{TP + TN}}{{TP + TN + FP + FN}}, P = \frac{{TP}}{{TP + FP}}, R = \frac{{TP}}{{TP + FN}}, F1 = \frac{{2PR}}{{P + R}}。$ |
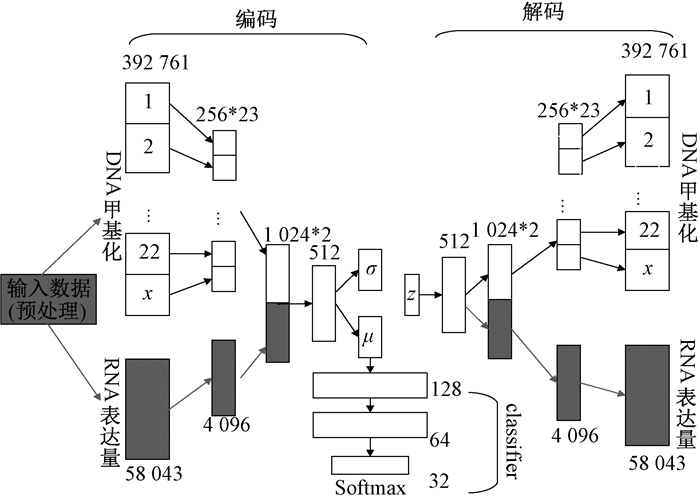
分别用VAE+CNN方法和VAE+classifier方法, 与本文方法(VAE+H-CNN)进行性能比较。此处的VAE+CNN为使用Python包NumPy完成融合数据一维到二维的转化后用CNN分类。VAE+classifier模型如图 7所示。
|
图 7 VAE+classifier模型 Fig. 7 VAE+classifier model |
为了验证融合数据的有效性,进行了不同类型数据的对比实验,结果如表 1所示。可以看出,本文方法在性能上优于其他两种方法,与用NumPy进行维度转化相比,希尔伯特曲线在一定程度上保留了原始数据的结构,各个位点的连续性得到的破坏程度相对最小,在数据降维及融合的过程中引入VAE保留了引起癌变的重要位点。较Softmax分类器而言,本文方法分类效果更佳, 说明通过本文方法处理后得到的数据有效性更强。同时,融合后的数据在总体性能上优于单一数据,RNA表达量和DNA甲基化从不同的层面影响了肿瘤的形成,VAE对两种数据的有效融合和提取数据的重要特征,使得肿瘤的预测更加精确。
|
|
表 1 不同类型数据的实验结果对比 Tab. 1 Comparison of experimental results with different types of data |
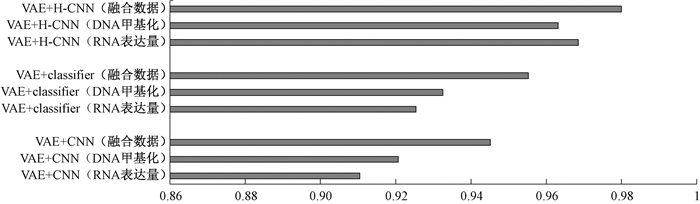
此外,本文对比了几种不同类型数据在三种方法上的分类精度,结果如图 8所示。可以看出,融合数据分类精度均高于单一数据类型,说明VAE在数据降维以及融合的过程中能够更好地提取数据特征,且在融合数据上本文方法优于其他两种方法。在三种数据类型上,VAE+CNN的分类精度都是最低的,表明用NumPy进行数据维度转化对数据结构的破坏程度较大。
|
图 8 分类精度的比较 Fig. 8 Comparison of classification accuracy |
为了对比不同方法在二分类问题上性能的优劣,挑选了神经细胞瘤和急性白血病的融合数据作为后续的实验数据。采用随机抽样的方式把共计4 240个样本分成两部分,其中2 968个样本作为训练集,1 272个样本作为测试集。将网络结构所对应的输出层参数进行调整,分别计算出不同性能指标的值,结果列于表 2。可以看出,在各个性能指标上,VAE+H-CNN均具有明显的优势,说明本文提出的网络结构在二分类问题上仍然具有很好的效果。
|
|
表 2 二分类问题性能比较 Tab. 2 Performance comparison of binary classification problems |
本文利用VAE对DNA甲基化和RNA表达量两种数据进行有效融合,将融合后的数据送入H-CNN网络,并运用希尔伯特曲线完成融合数据一维到二维的映射,将映射后的数据送入CNN网络进行后续分类。结果表明,无论是在多分类还是二分类任务上,各个性能指标均得到很大提升,在实验中表现出优异的性能,可以为肿瘤的临床诊断提供更加精确的指导。本文使用两种数据进行融合,提高了分类性能,如果能与病人的临床数据例如病人年龄、性别等进行结合,可能会进一步提高分类性能。
| [1] |
马敬敬. 基于智能算法的高维生物医学数据集的特征选择策略研究[D]. 开封: 河南大学, 2019. MA J J. Research on feature selection strategy of high-dimensional biomedical data set based on intelligent algorithm[D]. Kaifeng: Henan University, 2019. (  0) 0) |
| [2] |
封建邦. 基于主动学习的高维数据聚类算法研究[D]. 福州: 福州大学, 2016. FENG J B. High-dimensional data clustering algorithms based on active learning[D]. Fuzhou: Fuzhou University, 2016. (  0) 0) |
| [3] |
赵智通. 高维数据集降维优化研究[D]. 呼和浩特: 内蒙古大学, 2020. ZHAO Z T. A research on dimensionality reduction optimization for high-dimensional dataset[D]. Hohhot: Inner Mongolia University, 2020. (  0) 0) |
| [4] |
FERNÁNDEZ-MARTÍNEZ J L, FERNÁNDEZ-MUÑIZ Z. The curse of dimensionality in inverse problems[J]. Journal of computational and applied mathematics, 2020, 369: 112571. DOI:10.1016/j.cam.2019.112571 (  0) 0) |
| [5] |
师越, 董冬. 循环肿瘤DNA在肾细胞癌中的应用研究进展[J]. 检验医学, 2020, 35(9): 952-956. SHI Y, DONG D. Research progress of circulating tumor DNA in renal cell carcinoma[J]. Laboratory medicine, 2020, 35(9): 952-956. DOI:10.3969/j.issn.1673-8640.2020.09.023 (  0) 0) |
| [6] |
张亚丽, 李丝冰, 王艺, 等. 甲状腺癌中LZTS2蛋白表达及与BRAFV600E基因突变的关系[J]. 临床与实验病理学杂志, 2020, 36(9): 1057-1061. ZHANG Y L, LI S B, WANG Y, et al. Expression of LZTS2 protein in thyroid carcinoma and its correlation with BRAFV600E gene mutation[J]. Chinese journal of clinical and experimental pathology, 2020, 36(9): 1057-1061. (  0) 0) |
| [7] |
朱理, 汪翼. DNA甲基化与膀胱癌关系的研究进展[J]. 西南军医, 2020, 22(5): 424-428. ZHU L, WANG Y. Advances in the relation between DNA methylation and bladder cancer[J]. Journal of military surgeon in southwest China, 2020, 22(5): 424-428. DOI:10.3969/j.issn.1672-7193.2020.05.007 (  0) 0) |
| [8] |
KEIM D A. Pixel-oriented visualization techniques for exploring very large data bases[J]. Journal of computational and graphical statistics, 1996, 5(1): 58-77. (  0) 0) |
| [9] |
ANDERS S. Visualising very long data vectors with the Hilbert curve[R]. Cambridge: European Bioinformatics Institute, 2009.
(  0) 0) |
| [10] |
王攀, 赵洪林, 施睿峰, 等. 血浆中CDO1甲基化在肺癌早期诊断中的作用研究[J]. 中国肺癌杂志, 2020, 23(5): 314-320. WANG P, ZHAO H L, SHI R F, et al. The role of plasma CDO1 methylation in the early diagnosis of lung cancer[J]. Chinese journal of lung cancer, 2020, 23(5): 314-320. (  0) 0) |
| [11] |
翟正利, 梁振明, 周炜, 等. 变分自编码器模型综述[J]. 计算机工程与应用, 2019, 55(3): 1-9. ZHAI Z L, LIANG Z M, ZHOU W, et al. Research overview of variational auto-encoders models[J]. Computer engineering and applications, 2019, 55(3): 1-9. (  0) 0) |
| [12] |
沈克琳, 吉秉彧, 李然. 基于卷积神经网络的英文篇章情感量化方法[J]. 信阳师范学院学报(自然科学版), 2021, 34(1): 130-137. SHEN K L, JI B Y, LI R. Sentiment quantization of English texts based on convolutional neural networks[J]. Journal of Xinyang normal university (natural science edition), 2021, 34(1): 130-137. DOI:10.3969/j.issn.1003-0972.2021.01.022 (  0) 0) |
| [13] |
张玉宏. 深度学习之美[M]. 北京: 电子工业出版社, 2018. ZHANG Y H. The beauty of deep learning[M]. Beijing: Publishing House of Electronics Industry, 2018. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


