在各种灾害或战争后,地面通信设施往往无法正常使用,给救援任务带来了很大的困难[1-2]。因此,在紧急情况下恢复受影响地区的通信是极其重要的。无人机作为空中基站辅助通信,具有机动性高、成本低、灵活性大、覆盖范围广等优点,近年来得到了广泛的应用[3-4]。而面对日益复杂且多变的环境,单无人机难以满足任务需求,无人机集群协同作业将成为未来发展主流。
无人机集群辅助通信在工业界和学术界都得到了广泛的研究。许多研究者提出了通过优化目标函数[5]来改善无人机部署策略[6-12]。例如,最大化无人机的覆盖范围[3],最小化无人机消耗的能量[6],最小化无人机的发射功率[7],优化无人机轨迹[8-9],最小化无人机的数量[11-12]等。Zhao等[3]通过优化无人机覆盖的灾区范围,建立了一个统一的无人机辅助应急网络框架。Yang等[6]通过优化无人机的轨迹,研究了节能无人机与地面终端的通信。Sawalmeh等[7]使用粒子群算法和遗传算法优化无人机的动态轨迹,最小化无人机的发射功率,为灾区救援队提供无线覆盖。刘琨等[8]针对无人机航迹规划问题,提出了一种改进的人工蜂群算法,并采用禁忌搜索策略,将局部极值存入禁忌表中,帮助算法跳出局部最优解。Zhang等[11]通过优化无人机的三维定位优化了无人机的部署数量,并提出了一种基于人工蜂群的无人机部署数量最小化算法。Li等[12]提出了一种基于匹配交换理论的启发式算法,分配每个子周期访问无人机的用户来处理用户调度问题,并考虑了无人机能源效率的最大化。针对车辆计算任务的系统成本最小化问题,Zhao等[13]提出了一种基于软件定义网络(software defined network,SDN)的无人机辅助车辆计算卸载优化框架。
近年来,许多学习类算法也被应用到无人机集群通信工作中[14-17]。Liu等[14]提出了一种去中心化的深度学习框架,用以最大化任务中所有无人机的覆盖比例,并最大化潜在搜索地点的地理公平性,同时最小化总能耗。Cui等[15]开发了一个多智能体强化学习框架,使每个智能体通过学习发现其基于局部观察的最优策略,并提出了一个基于学习的动态资源分配算法。认识到加强灾害恢复能力的必要性,Erdelj等[16]描述了利用无线传感器网络技术和无人机来增强网络辅助灾害预测、评估和响应能力,并认为在自然灾害中,灾害管理人员的反应时间是挽救受灾地区人民生命的关键,并提出了针对地球物理、气候和气象灾害的网络架构。Kato等[17]提出利用人工智能优化天空地综合网络(space-air-ground integrated network,SAGIN),利用SAGIN提高用户的服务质量,并提出利用深度学习技术提高SAGIN的性能。
但在上述文献中,大多数对场景的假设过于简单,如:假设地面用户均匀静态分布;使用同构的无人机。这些都不符合实际。本文考虑了更现实的受灾地区用户移动的场景,在无人机网络连通性、地面用户覆盖阈值等约束条件下,提出并形式化将问题转化为无人机网络存活时间最大化的优化问题。同时提出了一种基于深度强化学习算法来解决这一问题,以达到实时决策。实验结果表明,与先进的深度强化学习算法相比,本文算法具有更快的收敛速度和较低的复杂度。
1 系统模型与问题描述本文考虑一个灾区紧急恢复网络的场景,其中多个异构无人机服务于指定水平区域的多个移动用户。假设集合M={1,2,…,m}表示地面移动用户。类似地,假设集合N={1, 2, …, n}表示无人机的集合。假设无人机使用不同的频率进行空对地和空对空通信,并分配正交信道以避免干扰。部署无人机后,地面用户绑定信噪比最高的无人机。
1.1 无人机与用户移动模型假设用户m随机分布,原始位置为(xm,ym,0)。无人机作为中继节点为地面移动用户提供网络服务,无人机i的三维坐标为(Xi,Yi,H)。假设所有的无人机都在一个恒定的高度H上飞行,对于用户m的位置表述为wm=(xm,ym,0),m∈M;同样地,对于无人机i的位置可以表示为Wi=(xi,yi,H),i∈N。
要求用户m的速度小于阈值Vmax,即
| $ \begin{equation*} 0 \leqslant v_{m} \leqslant V_{\max } 。\end{equation*} $ | (1) |
由于无人机是异构的,无人机i的最大飞行速度表示为Vmaxi,用户的最大速度不超过任意无人机最大速度,即
| $ \begin{equation*} V_{\text {max }} \leqslant \min \left\{V_{\max }^{i}\right\}, \forall i \in N 。\end{equation*} $ | (2) |
移动模型描述了不同网络场景下不同类型的用户移动行为或节点移动模式。可以分为个人用户/节点移动模型和群体移动模型。
假设用θi∈{0,1}给出无人机i的运行状态,要么不移动,要么移动。另外无人机i在t时刻的速度为vi, t=[vx,i,t,vy,i,t]。
如果移动用户要通过无人机服务,移动用户必须在无人机覆盖范围内,则需要满足的约束为
| $ \begin{equation*} d_{i, m}^{M, N} \leqslant R, \forall i \in N, m \in M, \end{equation*} $ | (3) |
其中:R为每个无人机的覆盖半径。
任意一个无人机与其相邻最近的无人机必须保持一定距离以避免碰撞,并保证一定距离以保持连接,
| $ \begin{equation*} d_{\min }^{M N} \leqslant d_{i j}^{N N} \leqslant d_{\max }^{N N}, \forall i, j \in N。\end{equation*} $ | (4) |
无人机之间使用空对空信道,这主要是视距(line of sight,LoS)连接。因此,无人机i和无人机j之间的路径损耗可以被建模为自由空间的传播损耗。即
| $ P L_{a}^{i j}=20 \lg d_{i j}+20 \lg f_{a}+20 \lg (4 \mathtt{π} / c), $ |
其中:dij是无人机i和无人机j之间的欧氏距离;fa是空对空信道的载波频率;c是光速。
1.2.2 空对地通信模型空对地信道通常分为LoS和非视线(NLoS)两部分连接。无人机i和用户m之间的路径损耗可表示为
| $ \begin{align*} P L_{g}^{i m}=p\left(L o S, \theta_{i m}\right) & \times P L_{L o S}^{i m}+ \\ \left(1-p\left(L o S, \theta_{i m}\right)\right) & \times P L_{N L o S}^{i m} \end{align*} $ | (5) |
其中: p(LoS, θim)是无人机i和用户m之间在仰角θim处出现LoS的概率;PLLoSim和PLNLoSim分别是LoS和NLoS连接的路径损耗。公式(5)中的p(LoS, θim)计算公式为
| $ p\left(L o S, \theta_{i m}\right)=\frac{1}{1+a \times \mathrm{e}^{-b\left(180 \theta_{i m} / \mathtt{π}-a\right)}}, $ |
其中:a和b是反映农村、城市等环境的恒定景观参数。公式(5)中的路径损失PLLoSim和PLNLoSim可分别表示为
| $ P L_{L o S}^{i m}=20 \lg d_{i m}+20 \lg f_{g}+20 \lg (4 \mathtt{π} / c)+\eta L o S, \\ P L_{N L o S}^{i m}=20 \lg d_{i m}+20 \lg f_{g}+20 \lg (4 \mathtt{π} / c)+\eta N L o S, $ |
其中:dim为无人机i与用户m之间的欧氏距离;fg为空对地信道的载波频率;ηLoS和ηNLoS分别为LOS和NLOS下的过度路径损耗,它们的值取决于环境。
考虑到上述的路径损耗模型,用户m与无人机i的信噪比SNRim可以计算为
| $ S N R^{i m}=10 \times \lg \frac{P W_{g}^{i} \times 10^{\frac{-P t_{g}^{i m}}{10}}}{N_{g w}}, $ |
其中:PWgi为无人机i的发射功率;PLgim为无人机i与用户m之间的路径损耗;Ngw代表稳定的高斯白噪声。
1.3 问题描述文献[10]中研究了在灾区部署最小数量异构无人机的问题。该工作在考虑地面用户移动的基础上进行,目的是在高度动态的无人机网络中最大化覆盖网络的生存时间。
为了使无人机网络的生存时间最大化,定义了以下约束。一个维数为1×N的无人机选择矩阵中的元素可以定义为
| $ a_{i}=\left\{\begin{array}{ll} 1, & \text { 如果无人机 } i \text { 被部署 }, \\ 0, & \text { 其他 }, \end{array} \forall i \in N。\right. $ |
则维数为M×N的无人机-用户关联矩阵中的元素可定义为
| $ b_{i m}= \begin{cases}1, & \text { 如果用户连接到无人机上, } \\ 0, & \text { 其他, } \end{cases} \\ \quad\quad\quad\quad\quad \forall i \in N, m \in M, $ |
要求任何地面用户只能被不超过一个无人机服务,表示为
| $ \begin{equation*} \sum\limits_{i \in N} b_{i m} \leqslant 1, \quad \forall m \in M , \end{equation*} $ | (6) |
此外,任何无人机同时服务的用户数量不能大于允许接入的最大并发连接数,表示为
| $ \begin{equation*} \sum\limits_{m \in M} b_{i m} \leqslant C_{i}, \forall i \in N_{\circ} \end{equation*} $ | (7) |
未部署的无人机不能服务于任何地面用户,即
| $ \begin{equation*} b_{i m} \leqslant a_{i}, \forall i \in N, m \in M_{\circ} \end{equation*} $ | (8) |
进一步定义维数为N×N的无人机-无人机连接矩阵中的元素,
| $ L_{i j}= \begin{cases}1, & \text { 如果 } S N R_{i j} \geqslant S N R_{a}, \\ 0, & \text { 其他 }, \end{cases} $ |
其中:SNRij代表从无人机i到j无线传输的信噪比;SNRa表示无人机之间的连接阈值。只有当SNRij≥SNRa时,无人机i才能与无人机j通信。SNRg表示无人机与地面用户的连接阈值,只有当SNRim≥SNRg时,无人机i才能为用户m服务。
在所有的无人机中,有些能够直接进入广域网(wide area network,WAN)进行数据上传。有些则要通过无人机自组织网多跳转发上传数据,无人机i的二元参数Ai表示可访问性,那么有
| $ A_{i}=\left\{\begin{array}{ll} 1, & \text { 如果无人机 } i \text { 连接到 WAN, } \\ 0, & \text { 其他 }, \end{array} \forall i \in N 。\right. $ |
接下来根据连接矩阵中的元素Lij定义无人机i的单跳邻居集Ni1为
| $ j \in N_{i}^{1}, L_{i j}=1, \forall i, j \in N。$ |
依此类推,可定义无人机k属于无人机i的2跳邻居集Ni2,即
| $ n \in N_{i}^{2}, k \in N_{j}^{1} \cup j \in N_{i}^{1}, \forall i, j, k \in N。$ |
类似的定义可以很容易扩展到无人机i的多跳邻居集。如果一个无人机属于至少一个可进入广域网的无人机的多跳邻居集,它就能进入广域网。因此,将无人机与广域网的连接性约束定义为
| $ \begin{equation*} \sum\limits_{n \in N_{i}^{*}, n \in N, * \in \mathbf{Z}} A_{i} \geqslant 1, \forall i \in N , \end{equation*} $ | (9) |
其中无人机n属于无人机i的*跳邻居集。
最后,所覆盖用户的百分比需要大于预定义的阈值τ,即
| $ \begin{equation*} \sum\limits_{i \in N} \sum\limits_{m \in M} b_{i m} \geqslant \tau \times M。\end{equation*} $ | (10) |
假设用户m被服务的时间为Tm,优化目标是将所有用户中最短被服务时间最大化,因此问题可以描述为
| $ \begin{equation*} \max\limits_{w_{i}, b_{i m}} \min T_{m}, \forall i \in N, m \in M。\end{equation*} $ | (11) |
同时受限于公式(1)~(10)。
文献[18]中证明了一般的无人机群部署是NP难问题。在连通性及覆盖率限制的条件下,要确定无人机能否通过移动对地面用户覆盖最长时间,这是本文的可行性问题。
2 基于DDPG的无人机多智能体深度强化学习改进算法 2.1 多智能体强化学习标准强化学习问题通常可以描述为马尔可夫决策过程(Markov decision processes,MDP),其中单个代理从与环境的交互中学习以实现特定目标。基于价值的方法,如深度Q网络(deep Q-network,DQN),已广泛应用于解决强化学习问题,然而由于动作空间的连续性,不能直接用于解决本文的强化学习问题。相比之下,诸如深度确定性策略梯度(deep deterministic policy gradirent,DDPG)这样的“演员-评论家”(Actor-Critic)结构可以通过学习策略空间上优化的参数化策略来处理此类问题。将代理的策略建模为θ参数化的βθ,主要思想是直接将θ沿策略梯度的方向调整,使奖励最大化。策略梯度可表示为
然而,从代理的角度上看,每个无人机都应用DDPG会使环境不稳定,降低整体性能。因此选择使用多智能体深度确定性策略梯度(multi-agent deep deterministic policy gradient,MADDPG)技术,该技术以集中的方式训练,同时促进测试中的分布式执行。多智能体的强化学习网络包含多架无人机,用户可在本地观察,其可以描述为多主体分散部分可观测马尔可夫决策过程(decentralized partially observable Markov decision process,Dec-POMDP),这是MDP的扩展。具体而言,Dec-POMDP由状态空间S、动作空间A和每个代理的观察空间O来定义。
在多智能体的深度强化学习中,代理在T个离散时间步长内顺序地与环境交互,在每个时间片t,代理的状态为st,其中第n个代理获得其局部观测on, t∈O(on, t是st的一部分),并产生动作an, t =βn, t(on, t)∈A,代理n根据自身的策略βn, t(on, t)完成动作,当所有的代理完成自己的动作时,代理n获得奖励值rn, t,状态st转变为新的状态st+1。对于多智能体任务,所有代理的目标是最大化总的预期回报
由于无人机间的连通性以及与用户的覆盖关系都取决于无人机与无人机(用户)的位置,因此每个无人机的观测向量都包括其位置以及用户的位置。第n个无人机的观测向量可以表示为
| $ \boldsymbol{o}_{n, t}=\left[w_{1, t}, w_{2, t}, \cdots, w_{M, t}, W_{1, t}, W_{2, t}, \cdots, W_{N, t}\right]。$ |
在获得局部观察后,每个代理使用其局部策略βn, t独立地确定自己的动作。对于本文的无人机代理,第n个无人机的动作为an, t=[vx, n, t, vy, n, t]。
2.1.3 无人机群奖励设置奖励设置最直接的方式是将第n个无人机所服务的最短用户时间减去其能量成本,另外加入保证连通性的惩罚项。即
| $ r_{t}=\sum\limits_{n=1}^{N} \sum\limits_{m \in M_{n}} \min \left\{T_{m}\right\}-\lambda \sum\limits_{n=1}^{N}\left(W_{n, t+1}-W_{n, t}\right)+\sum\limits_{n=1}^{N} c_{n}^{\text {con }}, $ |
其中:Mn是无人机n服务的用户集合,cncon是为保证无人机连通性而引入的惩罚项。
本文采用团队奖励值作为每个代理的奖励,这样每个代理的奖励变得相同,可以显著地降低训练复杂度。
2.2 算法结构模型考虑到每个代理都有相同的奖励,因此每个无人机代理的Q值应该是相同的。然而在MADDPG中每个代理都有自己的Critic网络,这就相当于每个代理都有自己单独的奖励,这不能利用每个无人机奖励相同这个设定。因此本文提出将Critic网络进行简化的改进MADDPG算法。
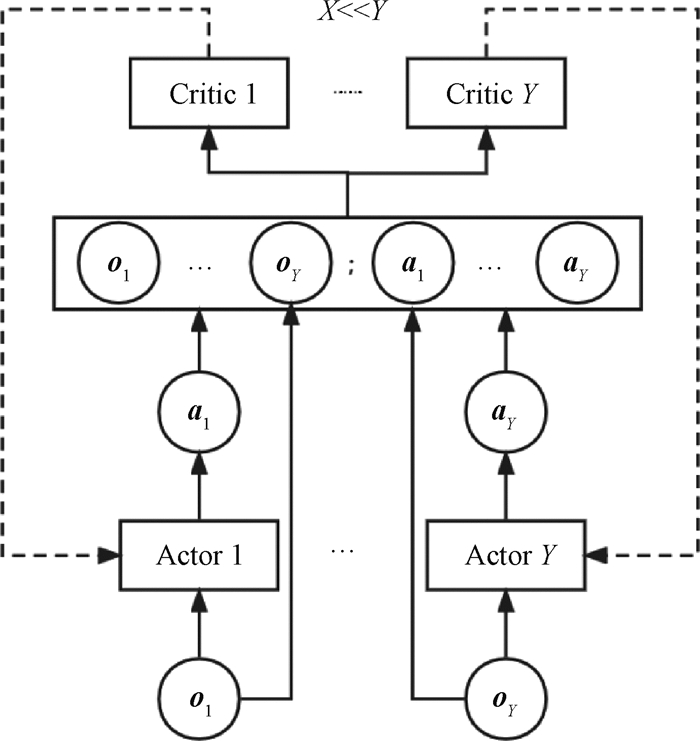
改进的MADDPG为所有的代理只训练少量的Critic网络,每个Critic网络将多个代理的行动和观察作为输入。因此,只使用少量的Critic网络就能够捕捉所有代理的策略变化,从而消除非平稳性。如图 1所示,算法中所有Y个代理共享X个Critic网络,其中X远小于Y,与标准的MADDPG算法相比,改进的算法大大降低了训练复杂度。
|
图 1 算法训练模型图 Fig. 1 Algorithm training model diagram |
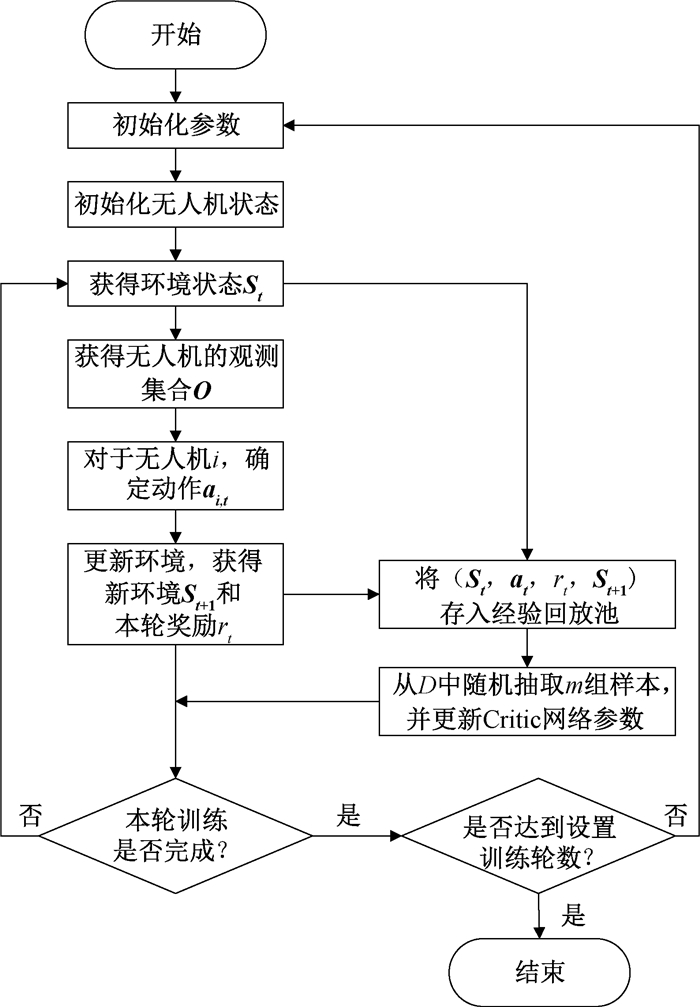
基于MADDPG的改进算法对无人机群进行训练,流程图如图 2所示。
|
图 2 算法流程图 Fig. 2 Algorithm flow chart |
本文使用tensorflow2.6.0在PyCharm上利用Python语言进行仿真模拟实验。实验场景借助OpenAI Gym进行模拟,该场景设置了一个1 000 m×1 000 m的区域,其中:M=20个;N=4架,海拔高度为H=100 m。只有“地平线距离”小于Dth=300 m的用户才能被无人机发现并连接到无人机。主要实验参数见表 1。
|
|
表 1 主要实验参数 Tab. 1 Main experimental parameters |
本文比较了五种基于深度强化学习的无人机轨迹控制方法,分别为:1) DDPG。为了解决连续动作控制问题而提出的一种深度确定性的策略梯度算法;2) MADDPG。DDPG在多智能体任务中的一种扩展;3) DQN。基于深度学习的一种Q-learning算法;4) Double DQN。针对对Q值过高估计的一种DQN改进算法;5) Dueling DQN。DQN的另一种改进算法。
本文分别从收敛效果和训练复杂度两个方面进行比较。
在设定的场景下进行25 000轮训练,不同训练轮次下的无人机群奖励值如图 3所示,MADDPG算法相比于DDPG具有更高的奖励,因为MADDPG采用的集中式Critic方法消除了训练过程中的非平稳问题。而DDPG的性能好于Double DQN和Dueling DQN,这是因为基于值的方法的操作空间只是DDPG的一个子集。而本文提出的算法比MADDPG有更快的收敛速度和收敛精度,比DDPG算法具有更高的奖励值。

|
图 3 无人机群在各算法下的奖励值 Fig. 3 Reward values for UAV swarms with various algorithm |
将奖励函数中的覆盖用户得到的奖励值输出进行对比,本文算法与标准的MADDPG所得到的目标奖励函数相近并超过DQN算法的奖励函数,如图 3所示。但是与MADDPG相比,本文所提出的算法通过减少Critic网络数量,大幅度降低了算法整体复杂度。本文算法的Critic网络参数量复杂度为
本文采用了多智能体深度强化学习方法对使用无人机群辅助通信覆盖问题进行了研究,以最大限度延长网络覆盖时间。无人机和环境之间的交互由Dec-POMDP建模。为了消除训练的非平稳性,支持分散决策能力,采用了集中式训练和分布式执行框架。通过优化MADDPG的网络结构,提出了一种改进的MADDPG算法。与其他深度强化学习算法进行仿真比较,本文提出的算法具有更快的收敛效果和更低的训练复杂度。
| [1] |
PANDA K G, DAS S, SEN D, et al. Design and deployment of UAV-aided post-disaster emergency network[J]. IEEE access, 2019, 7: 102985-102999. DOI:10.1109/ACCESS.2019.2931539 (  0) 0) |
| [2] |
SAKANO T, FADLULLAH Z M, NGO T, et al. Disaster-resilient networking: a new vision based on movable and deployable resource units[J]. IEEE network, 2013, 27(4): 40-46. DOI:10.1109/MNET.2013.6574664 (  0) 0) |
| [3] |
ZHAO N, LU W D, SHENG M, et al. UAV-assisted emergency networks in disasters[J]. IEEE wireless communications, 2019, 26(1): 45-51. DOI:10.1109/MWC.2018.1800160 (  0) 0) |
| [4] |
LIU Z, ZHAN C, CUI Y, et al. Robust edge computing in UAV systems via scalable computing and cooperative computing[J]. IEEE wireless communications, 2021, 28(5): 36-42. DOI:10.1109/MWC.121.2100041 (  0) 0) |
| [5] |
SHAKHATREH H, SAWALMEH A H, AL-FUQAHA A, et al. Unmanned aerial vehicles (UAVs): a survey on civil applications and key research challenges[J]. IEEE access, 2019, 7: 48572-48634. DOI:10.1109/ACCESS.2019.2909530 (  0) 0) |
| [6] |
YANG J N, CHEN J J, YANG Z L. Energy-efficient UAV communication with trajectory optimization[C]//2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE). Piscataway: IEEE Press, 2022: 508-514.
(  0) 0) |
| [7] |
SAWALMEH A H, OTHMAN N S, SHAKHATREH H, et al. Wireless coverage for mobile users in dynamic environments using UAV[J]. IEEE access, 2019, 7: 126376-126390. DOI:10.1109/ACCESS.2019.2938272 (  0) 0) |
| [8] |
刘琨, 封硕. 面向无人机航迹规划的改进人工蜂群算法[J]. 郑州大学学报(理学版), 2021, 53(1): 74-79. LIU K, FENG S. Improved artificial bee colony algorithm for UAV path planning[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(1): 74-79. (  0) 0) |
| [9] |
CALAMONERI T, CORÒ F, MANCINI S. A realistic model to support rescue operations after an earthquake via UAVs[J]. IEEE access, 2022, 10: 6109-6125. DOI:10.1109/ACCESS.2022.3141216 (  0) 0) |
| [10] |
ZHANG B, SONG J P, LIU Z, et al. Genetic algorithm enabled particle swarm optimization for aerial base station deployment[C]//2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall). Piscataway: IEEE Press, 2021: 1-7.
(  0) 0) |
| [11] |
ZHANG C, ZHANG L Y, ZHU L P, et al. 3D deployment of multiple UAV-mounted base stations for UAV communications[J]. IEEE transactions on communications, 2021, 69(4): 2473-2488. DOI:10.1109/TCOMM.2021.3049387 (  0) 0) |
| [12] |
LI Y B, ZHANG H J, LONG K P, et al. Joint resource allocation and trajectory optimization with QoS in UAV-based NOMA wireless networks[J]. IEEE transactions on wireless communications, 2021, 20(10): 6343-6355. DOI:10.1109/TWC.2021.3073570 (  0) 0) |
| [13] |
ZHAO L, YANG K Q, TAN Z Y, et al. A novel cost optimization strategy for SDN-enabled UAV-assisted vehicular computation offloading[J]. IEEE transactions on intelligent transportation systems, 2021, 22(6): 3664-3674. DOI:10.1109/TITS.2020.3024186 (  0) 0) |
| [14] |
LIU C H, MA X X, GAO X D, et al. Distributed energy-efficient multi-UAV navigation for long-term communication coverage by deep reinforcement learning[J]. IEEE transactions on mobile computing, 2020, 19(6): 1274-1285. DOI:10.1109/TMC.2019.2908171 (  0) 0) |
| [15] |
CUI J J, LIU Y W, NALLANATHAN A. Multi-agent reinforcement learning-based resource allocation for UAV networks[J]. IEEE transactions on wireless communications, 2019, 19(2): 729-743. (  0) 0) |
| [16] |
ERDELJ M, NATALIZIO E, CHOWDHURY K R, et al. Help from the sky: leveraging UAVs for disaster management[J]. IEEE pervasive computing, 2017, 16(1): 24-32. DOI:10.1109/MPRV.2017.11 (  0) 0) |
| [17] |
KATO N, FADLULLAH Z M, TANG F X, et al. Optimizing space-air-ground integrated networks by artificial intelligence[J]. IEEE wireless communications, 2019, 26(4): 140-147. DOI:10.1109/MWC.2018.1800365 (  0) 0) |
| [18] |
ZHANG X, DUAN L J. Energy-saving deployment algorithms of UAV swarm for sustainable wireless coverage[J]. IEEE transactions on vehicular technology, 2020, 69(9): 10320-10335. DOI:10.1109/TVT.2020.3004855 (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


