图像处理中常用的圆检测算法有:基于Hough变换的圆检测[1-2]算法; 基于随机抽样一致性(random sampling consistency, RANSAC)算法的圆检测.Hough变换圆检测算法要遍历三维参数空间,对内存和时间的消耗特别大,且检测结果精度受参数离散化程度的影响也大.文献[3]提出了随机Hough变换(RHT)算法,该算法随机抽取图像空间中的3个点,对应到参数空间中的1个点,再从参数空间中选取候选圆并进一步挑出真实圆,从而大大减少了内存消耗.RANSAC算法[4]与RHT算法相似,但其抽样的目的在于估计出一个能包含尽可能多的边界点的圆模型,只用圆模型上的点来拟合真实圆.这两种算法的共同缺点在于大量圆外点会带来大量无效抽样和累积.文献[5]用梯度法预先判断3点是否在候选圆上,减少了无效采样,但计算梯度本身也要消耗不少时间.文献[6]则对每条连续边界3等分,再分别取点进行圆拟合,该方法仅对连续边界进行取样,大大减少了对无效点的抽样.但这两种改进算法都只用3个点得到圆参数,准确度有限.文献[7]用最小二乘法改进了RHT算法,先用4点确定初始圆参数,再对得到的圆上点迭代使用最小二乘法,直至没有新点加入,该方法准确性较好,但所需迭代次数受初始参数影响大.本文设计了一种改进的RANSAC圆检测算法,可以进一步减少检测圆所需时间并保证其准确度.
1 RANSAC算法传统RANSAC圆检测算法的具体步骤如下:
1) 对待检测的图像进行预处理及边缘提取,建立由所有边缘点坐标构成的点集D.令当前循环次数k=0.
2) 初始化局内点点集Inpts=NULL.从边界点点集D中随机抽取3个点,计算这3个点所确定的圆的参数[a, b, r](圆心(a, b).半径r),若圆的半径r的范围在预设的范围之内,则转3);否则转6).
3) 计算各边界点到2)中所得到的圆的圆心的距离d,若d-r≤ε(ε为可接受的局内点偏离裕度),则认为该点为局内点,将其坐标存入局内点点集Inpts,否则视为局外点.
4) 计算该圆上的局内点点数M,若M大于阈值Mmin,则认为此次估计出的圆模型足够合理,这些局内点也可视为有效点,转5);否则转6).
5) 对点集Inpts中的所有点用最小二乘法重新计算圆的参数模型,得到最终结果.
6) k=k+1,若k>Kmax,则结束; 否则转2).
2 改进的RANSAC算法传统RANSAC算法中抽样耗时占算法总耗时的比重较大,而非圆边界点(即局外点)的数量又是影响所需抽样次数的最主要的因素.所以,减少局外点数量对减少算法总耗时有较大作用.另外,传统算法通过三点预估圆方法选取的局内点点集的随意性较大,这使得最终得到的检测结果的随意性也较大,为改善这一点,可以考虑综合使用多组局内点点集进一步地拟合和筛选.本文根据以上思路对原算法进行改进.
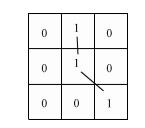
2.1 图像预处理为减少边缘提取中伪边缘带来的非圆边界点,本文在预处理环节中采用陷波滤波[8],针对性地滤去图像中金属本身的纹路.常用的边缘提取方法有:1)使用Sobel、Canny等算子直接提取.2)使用模糊分割等分割算法进行区域分割[9],再用形态学算法提取边缘.综合考虑算法准确性和耗时长短,本文使用Canny检测法进行边缘提取.待处理的图像如图 1所示.提取出的边缘如图 2所示.从图中可以看出,凹痕圆的边界基本被提取,金属纹路伪边缘大大减少.接着,为进一步减少凹痕固有的小裂纹带来的非圆边界点,本文对提取出的边缘进行连通域检测,并对检测出的所有8邻接连通区域进行标记.8邻接的示意图如图 3所示.然后,将这些连通区域存储到一个元胞数组中,每1个元胞代表 1个连通区域(即一条连续边界).最后通过统计的方法将小边界去除,仅对较长的连续边界进行抽样.

|
图 1 待检测凹痕图像 Figure 1 The picture of dent for detection |
|
图 3 8邻接示意图 Figure 3 The sketch of 8-adjacency pixels |
|
|
表 1 3种算法检测结果 Table 1 The detection results of three algorithms |
通常,由三点确定圆参数的方法是将三点的坐标代入圆的方程,联立三元方程求解得到.本文则利用圆的圆心到弦的中点的连线垂直于弦这一特性,联立二元方程求出圆心坐标,然后求圆心到任意一点的距离即可得出半径.由于只需求解二元方程,比原算法更为简便.
假设圆心坐标为Z(a, b),三点坐标分别为A(x1, y1),B(x2, y2),C (x3, y3),可以得到二元方程:
| $ \left\{ \begin{array}{l} b - \frac{{{y_1} + {y_2}}}{2} = \frac{{{x_2} - {x_1}}}{{{y_2} - {y_1}}}(\frac{{{x_1} + {x_2}}}{2} - a), \\ b - \frac{{{y_1} + {y_3}}}{2} = \frac{{{x_3} - {x_1}}}{{{y_3} - {y_1}}}(\frac{{{x_1} + {x_3}}}{2} - a). \end{array} \right. $ | (1) |
从而可以很容易地得到圆心坐标(a, b),而半径即为[5]
| $ r = \sqrt {{{(a - {x_1})}^2} + {{(b - {y_1})}^2}.} $ |
在判定某点是否属于局内点时,本文由原判定公式|d-r|≤ε,得出(r-ε)2≤ d2≤(r+ε)2,若设某次估计出的圆的圆心为Z(a, b),某点坐标为I(xi, yi),则该公式变成(r-ε)2≤(xi-a)2+(yi-b)2≤(r+ε)2,从而避免了原方法中计算边界点到圆心的距离d时的开方运算,加快了速度.
若抽样所得圆的局内点个数大于阈值Mmin,则可判定该圆为候选圆.由于后期还有进一步的筛选,阈值可以根据多次试验的结果取一个相对较小的值以减少抽样时间.如果是第一次取到候选圆,我们可以综合原来判定候选圆局内点时的阈值ε估计出一个阈值ε2(ε2>ε),并认为满足d-r>ε2的点不属于所求圆的边界并将其排除,仅对剩下的点抽样以进一步提高后续抽样取到候选圆的概率.实验证明,在第一次得到候选圆后,可以很容易地连续得到候选圆.
如果在随机抽样中,已经有3~4次能够得到候选圆,那么真实圆的边缘存在于这些候选圆局内点中的概率就已经很大了.再继续抽样的意义不大.为控制总的检测时间,本文以4次为阈值,只要4次取到候选圆,就可以结束抽样循环
2.4 确定最终圆参数得到候选圆后,用最小二乘法对以上候选圆的局内点再进行圆拟合,可以得到更为精准的候选圆[10].然后,设定一个很小的距离阈值ε3(ε3 < ε),把原局内点中到新圆的边缘的径向距离小于阈值ε3的点作为新候选圆的局内点,比较各新候选圆局内点的个数N,选择N最大的新候选圆作为最终真实圆.相比原算法只选出一个候选圆进行最小二乘法拟合,本算法对多个候选圆进行拟合与精选,可以得到更准确更稳定的结果.
2.5 本文算法的具体步骤1) 对待检测的图像进行预处理及边缘提取,检测边缘点中所有的8邻接连通区域,排除长度较小的连通域,用剩余的较长的连续边界上的点构建边界点集D,初始化候选圆局内点单元集Pcir=NULL,候选圆参数单元集P=NULL,当前循环次数k=0,候选圆个数Nt=0.然后,为最大抽样次数Kmax设定一初始值.
2) 初始化局内点点集Inpts=NULL.从边界点点集D中随机抽取3个点,计算这3个点所确定的圆的参数[a, b, r](圆心(a, b),半径r),若半径r的范围在预设的圆的半径范围之内,则转3);否则转6).
3) 计算各边界点到2)中所得到的圆的圆心的距离d,若|d-r|≤ε(ε为可接受的局内点偏离圆的边缘的裕度),则认为该点为局内点,将其坐标存入局内点点集Inpts,否则视为局外点.
4) 计算该圆上的局内点点数M,若M大于阈值Mmin,则认为该圆可以作为候选圆,将局内点点集Inpts作为一个单元pcir,存入候选圆局内点单元集Pcir,转5);否则转6).
5) Nt=Nt+1, 若Nt≥4,则结束循环,转8);若Nt=1,则计算边界点到该候选圆的圆心的距离d,从边界点点集D中排除满足|d-r|>ε2的点,再转6);若1 < Nt < 4,直接转6).
6) k=k+1,若k>Kmax,则结束循环,转7);否则转2).
7) 若Nt < 2,则Kmax自加10,再转2);否则转8).
8) 对各候选圆局内点单元pciri(i=1, 2, …,Nt)分别进行最小二乘法圆拟合,将得到的新的候选圆参数pi=[ai, bi, ri]作为一个单元存入候选圆参数单元集P中,计算各候选圆的局内点到由该候选圆重新拟合出的圆心[ai, bi]的距离di,从这些局内点中找出满足|di-ri|≤ε3的局内点,并排除pciri中其他的点.初始化候选圆局内点数目集NP=NULL,将新的候选圆局内点的个数存入NP中.比较各候选圆的局内点个数,找出局内点个数最大的候选圆,并将其参数[ai, bi, ri]作为最终得到的真实圆的圆参数.
3 实验结果为了检验本文算法的有效性,用该算法在VS2013平台下编写了实验程序,并将其用于布氏硬度压痕直径自动化测量仪器研制中.图 1即为用HB-3000B硬度计,10 mm直径淬硬钢球在用正火处理过的T10钢板上压出的凹痕图像,实验载荷为29.42 kN,成像用的CCD像素数为1 920×1 560.本实验用该方法在同一块钢板上共得到了10个凹痕(凹痕分布相对集中).实验要求测出凹痕直径并查表得出布氏硬度值[11].本文分别用上述3种算法对这10个凹痕进行检测,其结果如表 1所示.其中随机Hough变换(RHT)圆检测算法的具体步骤见文献[3].
表 1中的参考直径是用读数显微镜对这10个凹痕进行测量所得到的直径的平均值(括号内为测量所得直径的取值范围).从表中可以看出,本文算法所得直径相比其他两种算法更接近参考值,测量结果的方差也比其他两种方法更小.因此,本文算法提高了测量结果的准确性和稳定性.从检测时间上看,本文算法的耗时也明显比其他两种算法更短.
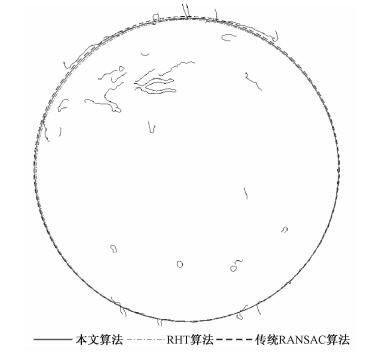
用以上3种算法检测得到的圆参数在图 2所示的边缘图像上画圆,其对比效果如图 4所示.从图中可以看出,3种算法检测出的圆对左上角的边缘的贴合程度有微小差异.为了更清楚地看出这些差异,图 5为图 4左上角的局部放大图.从图中可以看出,本文算法所得结果对图像边缘的贴合效果也优于其他两种算法.
|
图 4 3种算法拟合的圆的对比 Figure 4 The differences among the fitting circles in three algorithms |
4 结论
本文对传统的RANSAC圆检测算法从无效点的排除、候选圆的选取、真实圆的确定等方面进行了改进,实验结果表明,该算法结果在准确性、稳定性、运算时间3个方面均明显优于传统RANSAC圆检测算法,而且也优于目前常用的RHT圆检测算法,完全能够满足实时检测需求.
| [1] |
LI G Q, ZHANG L X, YU Z P, et al. Research of edge detection algorithm based on Canny algorithm and Hough transform[J]. Advanced materials research, 2014, 1039: 262-265. DOI:10.4028/www.scientific.net/AMR.1039 (  0) 0) |
| [2] |
BOUKHAROUBA A. A new algorithm for skew correction and baseline detection based on the randomized Hough transform[J]. Journal of King Saud university-computer and information sciences, 2017, 29(1): 29-38. DOI:10.1016/j.jksuci.2016.02.002 (  0) 0) |
| [3] |
王新, 张元东, 王莉. 一种随机Hough变换检测圆的优化方法[J]. 测控技术, 2016, 35(6): 112-116. (  0) 0) |
| [4] |
袁清珂, 张振亚, 毕庆. 改进的RANSAC算法在直线拟合中的应用[J]. 组合机床与自动化加工技术, 2015, 1(1): 123-125. (  0) 0) |
| [5] |
袁理, 曹智睿. 改进的随机Hough变换圆检测算法[J]. 计算机应用, 2010, 30(S1): 174-176. (  0) 0) |
| [6] |
陈小艳, 王强, 李柏林. 改进的Hough变换检测圆方法[J]. 计算机系统应用, 2015, 24(8): 197-201. (  0) 0) |
| [7] |
霍建亮, 曾翎, 王德胜, 等. 基于最小二乘法改进的随机圆检测算法[J]. 光电工程, 2011, 38(5): 145-150. (  0) 0) |
| [8] |
阮秋琦. 数字图像处理学[M]. 北京: 电子工业出版社, 2013.
(  0) 0) |
| [9] |
刘洪普, 杨乐, 侯向丹, 等. 一种改进的模糊C均值图像分割算法[J]. 郑州大学学报(理学版), 2017, 49(2): 66-71. (  0) 0) |
| [10] |
牛方君, 曹慧慧. 利用最小二乘法测量半径样板半径[J]. 电子产品可靠性与环境试验, 2015, 33(6): 56-58. (  0) 0) |
| [11] |
文九巴. 金属材料学[M]. 北京: 机械工业出版社, 2011.
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50



