我国残疾人数量较为庞大,就目前的医疗水平而言,穿戴假肢是其恢复行动能力的唯一途径.随着科技的发展,传统的被动型假肢已无法满足截肢者的需求.因此,主动型假肢的研究十分关键[1].国外对于主动型假肢的研究起步较早,其中应用较为广泛的控制方法如有限状态机、鲁棒控制等[2-4].目前较为成熟的假肢产品如德国Otto Bock公司的C-Leg、Genium系列假肢,冰岛Ossur公司的Symbionic Leg、Rheo Knee系列假肢等[5].近年来,国内对于主动型假肢的研究也取得了很多成果,设计了一些智能假肢膝关节[6-8].但由于主动型假肢结构复杂且受到的内外扰动较多, 这些特点给假肢控制器的设计带来很大困难,限制了假肢性能的进一步提高.
自抗扰控制(active disturbance rejection control,ADRC)是在经典PID控制的基础上提出的一种非线性控制策略[9-11].其继承了经典PID方法不依赖于模型的优点,仅利用误差反馈进行控制,同时,又通过建立扩张状态观测器(extended state observer,ESO)对内外扰动进行估计和补偿,进而将误差的线性组合改为非线性组合,进一步改善了控制效果.考虑到自抗扰控制器的上述优点,以及假肢系统对于控制性能的要求,本文将自抗扰控制应用到主动型下肢假肢的控制中,建立了下肢假肢动力学模型,并为其设计了一种自抗扰控制策略.仿真实验结果表明,这种控制方法控制精度较高,可以实现假肢侧与健肢侧的协调摆动,从而使得残疾人能够正常行走.
1 下肢动力学模型分析分析人体下肢运动,首先需要建立其动力学模型.在之前的下肢动力学研究中,往往在建模分析时对下肢进行一定程度上的简化,这样的模型并不能真实地反映下肢的运动状态.而且,由于人体下肢运动的复杂性和外作用力的时变性,直接对其应用机理建模法进行动力学建模确实难度较大.因此,本文借鉴文献[12]中的建模方法,利用实际测量得到的人体行走时的下肢膝关节的力矩数据和角度数据,应用曲线拟合的辨识方法得到膝关节的力矩-角度关系,进而得到下肢运动的动力学模型.文献[13]中所建立的关节力矩-角度模型是一阶系统,这与现实情况略有不符.由物理学规律可知,对于一个多连杆系统而言,其动力学方程[14]可以表示为
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{q,\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{q}} \right), $ | (1) |
式中:q、
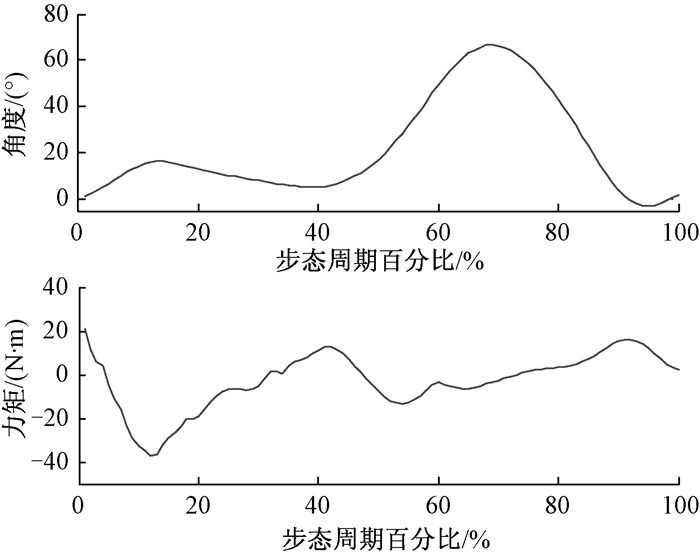
|
图 1 一个步态周期内的下肢动力学数据 Figure 1 The normal dynamical gait data in a stride |
本文应用Matlab软件中的System Identification工具箱对系统进行建模.源数据的采样时间为0.01 s,一个步态周期为0.99 s,共100个点.在进行曲线拟合时发现,一个完整的步态周期的动力学数据无法借助一个单一的二阶系统进行描述,故将一个步态周期的数据分为四段分别进行建模,时间区间为[0, 0.24]、[0.25, 0.45]、[0.46, 0.86]、[0.87, 0.99],从而得到完整的下肢动力学模型为
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - 111.7{x_1} - 9.818{x_2} - 10.38\tau ,\\ y = {x_1}, \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - 0.002\;693{x_1} - 7.516{x_2} + 190.3\tau ,\\ y = {x_1}, \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - 97.95{x_1} - 11.95{x_2} - 831.7\tau ,\\ y = {x_1}, \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = - 57.3{x_1} - 0.133\;6{x_2} + 390.1\tau ,\\ y = {x_1}, \end{array} \right. $ | (5) |
式中:y表示膝关节角度;τ表示膝关节力矩.
为了保证所得模型的正确性,需要对其进行检验.将四段膝关节力矩作为模型的输入,对比得到的输出与对应的膝关节角度,曲线拟合结果如图 2所示.可见,所建立的模型能准确地描述下肢的真实运动状态.
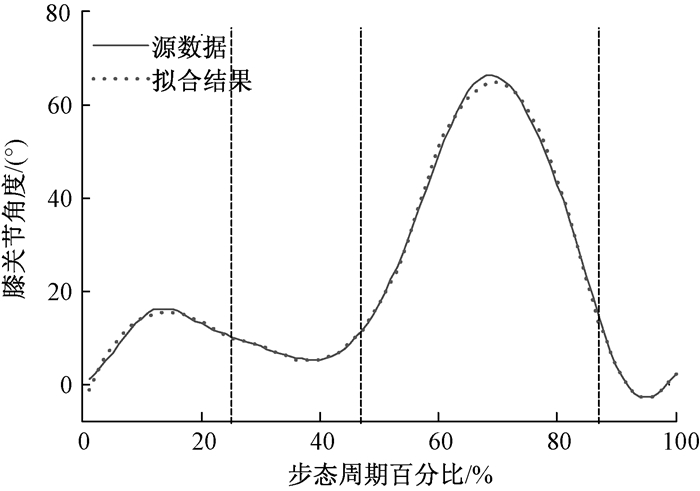
|
图 2 曲线拟合结果 Figure 2 The curve of fitting result |
为使下肢截肢者能恢复正常行走能力,须保证假肢侧与健肢侧的运动协调一致.本文研究中所采用的下肢假肢结构如图 3所示,由于主要研究对下肢假肢膝关节的控制,故只在假肢膝关节处设置了动力驱动装置,假肢踝关节处仍采用被动型踝关节.动力装置选择直线电机,优点在于结构简单,运动平稳,定位精度高.
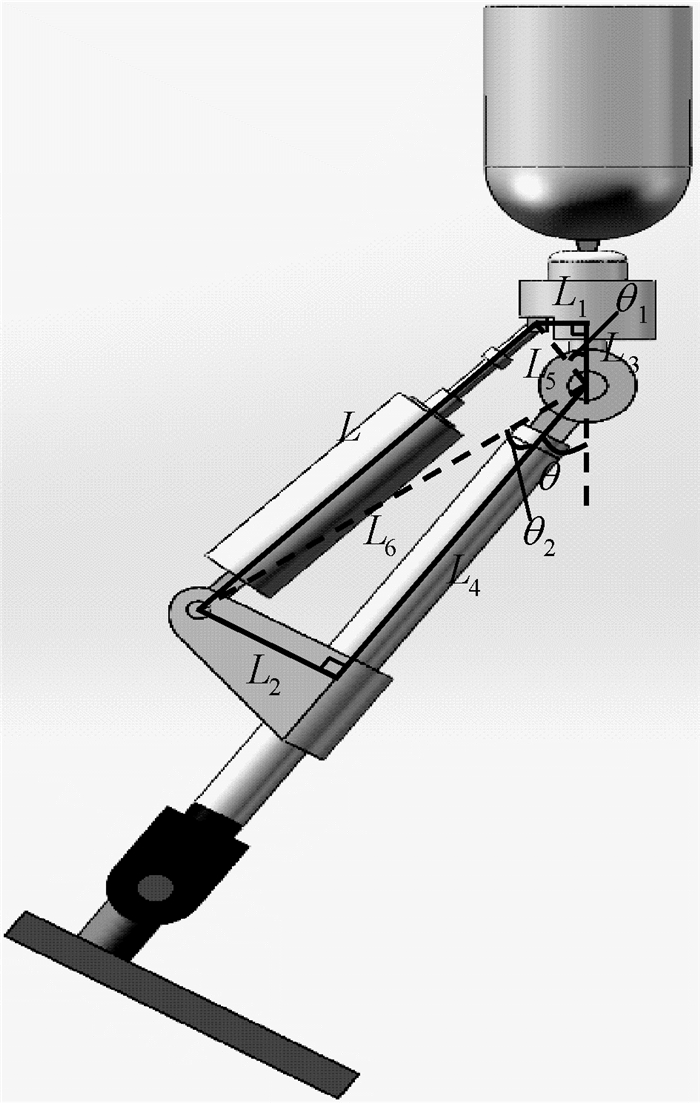
|
图 3 下肢假肢结构 Figure 3 The structure of the lower limb prosthesis |
假肢的驱动原理十分简单,电机的一端固定于假肢大腿杆处,接受腔下方,另一端固定于小腿杆处.残疾人行走时,假肢接受腔及大腿杆随残肢一起摆动,在步态周期的不同时刻,只要适当地调节电机的输出力,即可改变电机轴的伸缩长度,从而使小腿杆摆动到合适的位置,实现对正常行走状态的模拟.
根据得到的健康人行走时的膝关节力矩,结合电机的结构参数以及其在假肢大腿杆和小腿杆上的安装尺寸,可以计算出一个步态周期内电机输出力的大小.如图 3所示,L为电机的总长度,θ为膝关节角度,L1、L2、L3、L4、θ1、θ2为假肢的结构参数,其中L1、L2、L3、L4分别为26、75、42、238 mm,θ1为31.76°,θ2为17.49°.
由假肢的机械结构及余弦定理可得
| $ L_1^2 + L_3^2 - L_5^2 = 2{L_1}{L_3}\cos {\theta _1}, $ | (6) |
| $ L_2^2 + L_4^2 - L_6^2 = 2{L_2}{L_4}\cos {\theta _2}, $ | (7) |
| $ L_5^2 + L_6^2 - {L^2} = 2{L_5}{L_6}\cos {\theta _3}, $ | (8) |
式中:θ3=π-θ1-θ2-θ,其余变量的含义见图 3.膝关节驱动电机的输出力F与膝关节力矩τ存在如下关系:
| $ F = \tau \frac{{{\rm{d}}{\theta _3}}}{{{\rm{d}}L}} = \frac{{\tau \sqrt {L_5^2 + L_6^2 - 2{L_5}{L_6}\cos {\theta _3}} }}{{{L_5}{L_6}\sin {\theta _3}}}, $ | (9) |
其中L5、L6可由式(6)、(7)计算得到.由式(9)可得到一个步态周期内电机输出力曲线,结果如图 4所示.
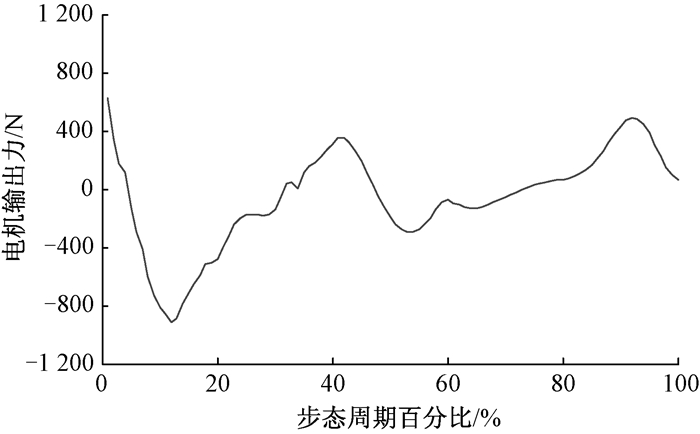
|
图 4 电机输出力曲线 Figure 4 The output force curve of the motor |
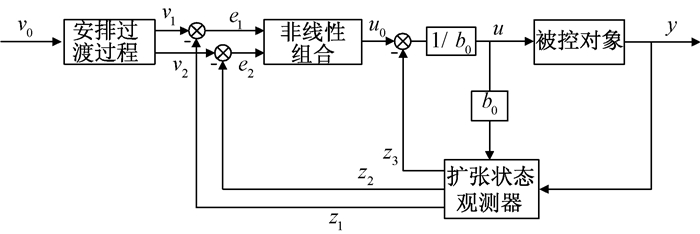
自抗扰控制是一种对模型精确程度要求较低的控制算法,它可以较好地抑制系统中存在的扰动,比较适合假肢这类存在各种不确定性的非线性系统.因此,本文将自抗扰控制方法应用于主动型膝上假肢的控制.典型二阶系统的自抗扰控制系统如图 5所示,它由跟踪微分器、扩张状态观测器误差的非线性组合和扰动补偿等环节组成.
|
图 5 自抗扰控制系统 Figure 5 The active disturbance rejection control system |
为优化控制过程的动态特性,自抗扰控制方法中引入了跟踪微分器,实现了对设定信号及其一阶微分的双重跟踪,从而柔化了误差信号.跟踪微分器的形式可以表示为
| $ \left\{ \begin{array}{l} e = {v_1} - {v_0},\\ {v_1} = {v_1} + h{v_2},\\ {v_2} = {v_2} + h \cdot fhan\left( {e,{v_2},r,h} \right), \end{array} \right. $ | (10) |
式中:v0为设定信号;v1是对v0的跟踪信号;v2是对v1的微分信号;h为系统的采样时间;fhan(·)是最速综合函数,含有r和h两个参数,决定了对设定信号跟踪的快慢程度.对于形如fhan(x1, x2, r, h)的最速综合函数,其具体表达形式为
| $ \left\{ \begin{array}{l} d = rh,\\ {d_0} = hd,\\ y = {x_1} + h{x_2},\\ {a_0} = \sqrt {{d^2} + 8r\left| y \right|} ,\\ a = \left\{ {\begin{array}{*{20}{l}} {{x_2} + \frac{{{a_0} - d}}{2}{\rm{sign}}\left( y \right),}&{\left| y \right| > {d_0},}\\ {{x_2} + y/h,}&{\left| y \right| \le {d_0},} \end{array}} \right.\\ fhan = - \left\{ {\begin{array}{*{20}{l}} {r{\rm{sign}}\left( a \right),}&{\left| a \right| > d,}\\ {ra/d,}&{\left| a \right| \le d.} \end{array}} \right. \end{array} \right. $ | (11) |
主动型膝上假肢在工作过程中受到多种不确定性因素的影响,为对其进行补偿,本文通过构造扩张状态观测器对系统的各状态量进行估计并补偿.扩张状态观测器的形式可以表示为
| $ \left\{ \begin{array}{l} e = {z_1} - y,\\ {{\dot z}_1} = {z_2} - {\beta _{01}}e,\\ {{\dot z}_2} = {z_3} - {\beta _{02}} \cdot fal\left( {e,0.5,\delta } \right) + {b_0}u,\\ {{\dot z}_3} = - {\beta _{03}} \cdot fal\left( {e,0.25,\delta } \right), \end{array} \right. $ | (12) |
式中:y为系统输出;z1、z2、z3分别为系统输出y、输出的一阶微分
| $ fal\left( {e,\alpha ,\delta } \right) = \left\{ {\begin{array}{*{20}{l}} {e/{\delta ^{\alpha - 1}},}&{\left| e \right| \le \delta ,}\\ {{{\left| e \right|}^\alpha }{\rm{sign}}\left( e \right),}&{\left| e \right| > \delta .} \end{array}} \right. $ | (13) |
通过扩张状态观测器可以对系统的扰动a进行很好的估计,从而在控制过程中进行补偿.自抗扰控制的状态误差反馈率是对系统输出误差e及系统输出微分的误差
| $ \left\{ \begin{array}{l} {e_1} = {v_1} - {z_1},\\ {e_2} = {v_2} - {z_2},\\ {u_0} = {\beta _1} \cdot fal\left( {{e_1},{\alpha _1},\delta } \right) + {\beta _2} \cdot fal\left( {{e_2},{\alpha _2},\delta } \right), \end{array} \right. $ | (14) |
式中:fal(·)为式(13)所示的非线性函数;β1、β2为一组参数.
最后,对系统的误差反馈控制量u0用扰动估计值z3的补偿来确定最终控制量,可以表示为
| $ u = \frac{{{u_0} - {z_3}}}{{{b_0}}}, $ | (15) |
式中:b0为补偿因子,可以通过调节其大小来改变补偿作用的强弱.
4 仿真实验为验证所提出的控制方法的可行性,利用Solidworks、Adams和Matlab软件对残疾人的平地行走运动进行仿真,通过观察模型的行走过程是否平稳、正常,来判断控制效果的优劣.
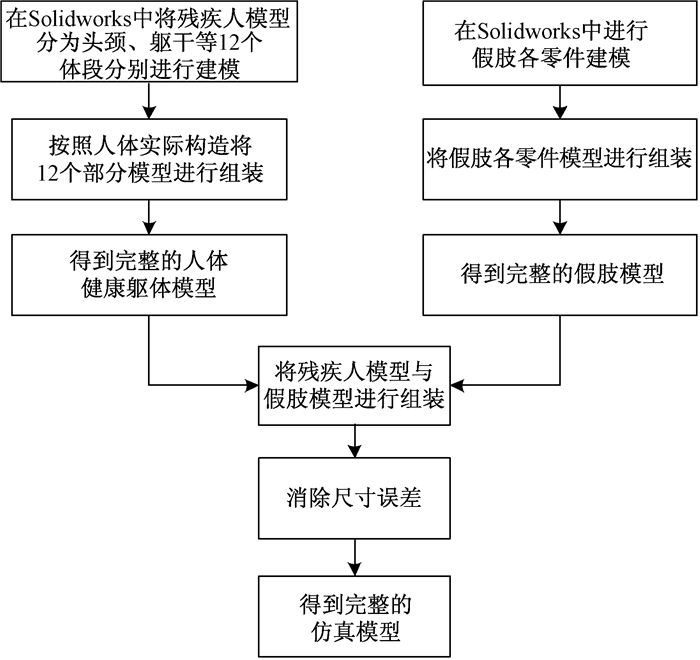
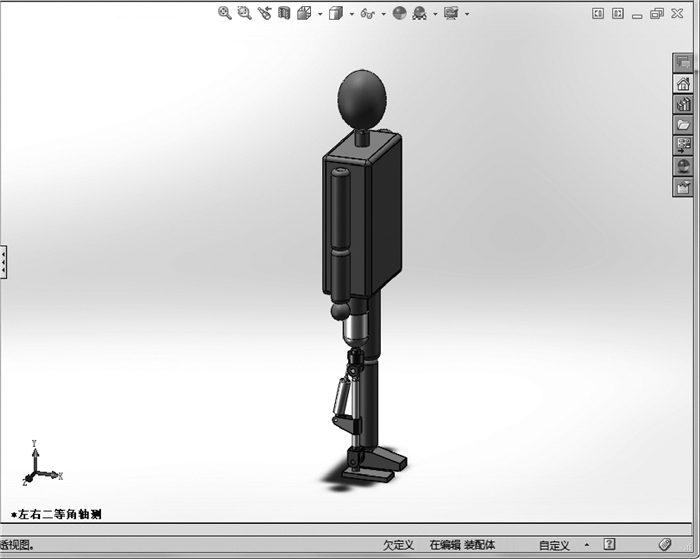
4.1 Solidworks三维实体建模进行残疾人平地行走仿真,首先需要在Solidworks软件中建立残疾人和下肢假肢的三维实体模型.本文在保证残疾人的运动特征和主要参数不变的情况下,对残疾人模型进行了一定程度的简化.在建模过程中,将残疾人分为头颈,躯干,左右上臂,左右前臂,左右手,健肢侧大腿、小腿、足以及残肢等12个体段分别进行建模,各体段的尺寸参数由GB/T 10000—1988《中国成年人人体尺寸》[15]得到.建模流程如图 6所示,在Solidworks软件中建立的残疾人与假肢装配模型如图 7所示.
|
图 6 Solidworks建模流程 Figure 6 Modeling process in Solidworks |
|
图 7 Solidworks装配模型 Figure 7 The assembly model in Solidworks |
三维实体模型创建完成后,导入到Adams软件中实现残疾人的平地行走仿真,进行仿真时所涉及的各体段的质量、质心位置、转动惯量等参数参照GB/T 17245—2004《成年人人体惯性参数》[16].假肢部分的动力学参数则参照其设计参数进行设置.此外,进行残疾人的行走仿真,还需要在软件中建立平地模型.
各部分的动力学参数设置完成后,需要根据实际的人体运动确定各体段间的相对运动形式,以对其添加运动约束.由于本文研究的主要是下肢的运动,故将头颈、躯干、左右手臂等体段以固定副的形式连接在一起.大腿与躯干之间的相对运动形式为旋转运动,故在躯干与大腿之间添加旋转副以模拟髋关节.同理,在大腿与小腿之间添加旋转副以模拟膝关节,在小腿与脚之间添加旋转副以模拟踝关节.假肢部分的运动约束同样根据其机械结构进行设置.对于地面模型而言,其在仿真过程中是固定的,所以对其添加固定副.除此之外,由于本文只研究残疾人在矢状面内的行走运动,所以在残疾人模型与地面模型之间添加平行约束,以保证其在行走过程中不会出现冠状面内的倾倒现象.
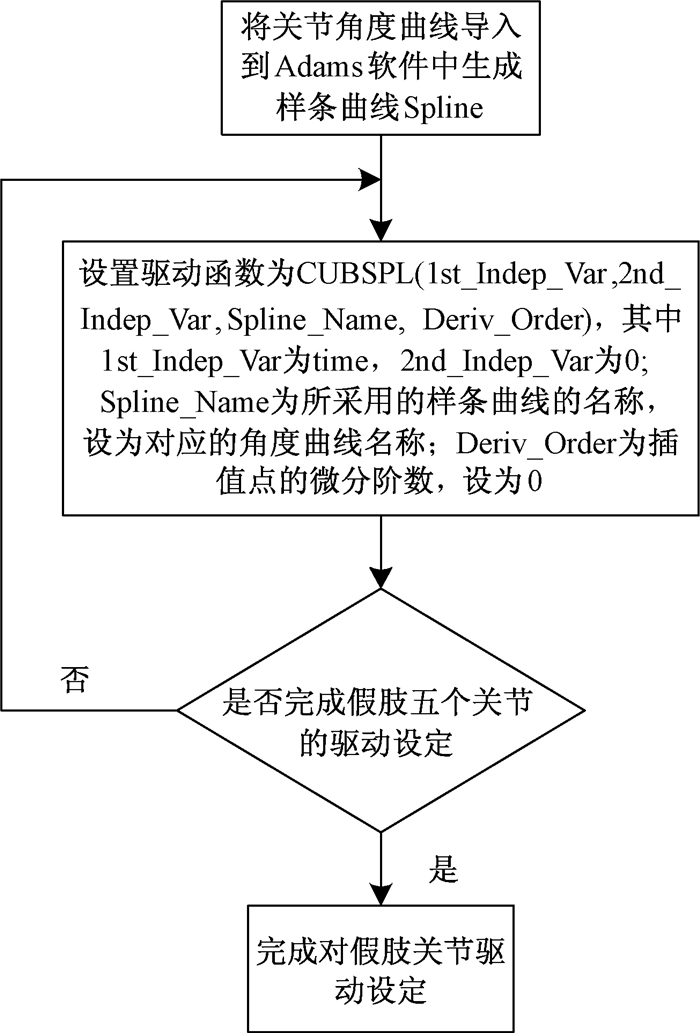
为使模型能够实现预期的运动,还需要在各约束上添加适当的驱动,并设置模型足部与地面间的接触形式.在Adams软件中,对运动副的驱动形式主要分为平动驱动和转动驱动两种,而可以作为驱动的物理量则有多种,如角度、角速度、位移、速度、力、力矩等.由于本文所验证的主要是假肢膝关节的控制方法的可行性,故对于模型健肢侧髋、膝、踝关节和残肢侧髋、踝关节的驱动均选择转动驱动,驱动变量选择角度,而残肢侧膝关节是由电机提供动力而进行运动的,故在假肢模型的电机处设置平动驱动,驱动变量选择力.两腿侧5个关节的驱动设置流程如图 8所示.
|
图 8 关节驱动设置流程 Figure 8 Joint drive setting process |
对于假肢电机处的作用力,为达到验证控制方法的目的,将其定义为状态变量,在Adams软件中定义一个状态变量Force,然后利用VARVAL函数将其与模型中的电机输出力关联起来,作为仿真系统的输入变量.利用相同方法将假肢膝关节状态变量Angle进行关联.对于模型足部与地面间的接触作用,在软件中依靠Contact功能实现,作用类型选择刚体对刚体,设置模型足部与地面间各接触参数,最终创建完成Adams仿真模型.
最后,利用软件中的Adams/Controls模块搭建Adams与Matlab两个软件的通信接口,设置好系统的输入、输出变量以及联合仿真的目标软件,从而将创建好的Adams模型导出生成m文件,此文件可以在Matlab软件中打开,生成对应的Simulink模块,此模块即作为控制系统的被控对象.进而,根据所采用的自抗扰控制方案完成整个控制系统的搭建.
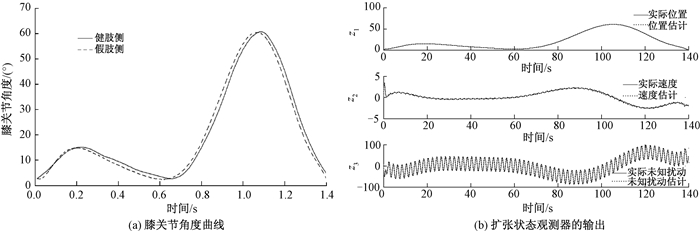
4.3 Adams与Matlab联合仿真仿真进行时,Matlab软件与Adams软件进行实时的数据交互,数据交换的时间可以人为设定,本文取0.05 s.在控制程序运行时,Matlab软件将计算得到的系统控制量,即电机的输出力Force实时传送到Adams软件中,Adams软件根据输入的控制量进行实时的三维运动仿真,并将系统的状态量,即假肢膝关节角度Angle反馈给Matlab,从而进行下一步控制量的计算.平地行走时控制效果如图 9所示.从图 9(a)可以看出,跟踪效果良好,能够快速无超调地跟随健肢侧输入.图 9(b)为扩张状态观测器的输出,分别为平地行走时的位置估计、速度估计以及未知扰动估计.通过将假肢未知以及未建模部分作为内部扰动并反馈补偿,控制系统取得良好的轨迹跟踪及控制性能,可见模型的行走过程平稳、正常,说明了本文所提出的控制方法是正确、有效的.
|
图 9 控制效果图 Figure 9 The diagram of control effect |
对主动型下肢假肢的控制问题进行了深入研究,将自抗扰控制方法应用到假肢的控制当中.首先分析了人体下肢的动力学特性,利用曲线拟合的方法建立其动力学模型,然后分析了下肢假肢的结构.在此基础上,考虑到模型中的不确定性和内外干扰等影响,本文设计了一种自抗扰控制方法.利用Solidworks、Adams和Matlab软件搭建了残疾人行走仿真系统,对所设计的控制方法进行仿真实验.结果表明,所设计的控制方法控制效果好、精度高,能实现残疾人健肢与残肢的协调摆动,从而使其恢复行走能力.
| [1] |
杨鹏, 刘作军, 耿艳利, 等. 智能下肢假肢关键技术研究进展[J]. 河北工业大学学报, 2013, 42(1): 76-80. (  0) 0) |
| [2] |
SUP F, VAROL H A, GOLDFARB M. Upslope walking with a powered knee and ankle prosthesis: initial results with an amputee subject[J]. IEEE transactions on neural systems and rehabilitation engineering, 2011, 19(1): 71-78. DOI:10.1109/TNSRE.2010.2087360 (  0) 0) |
| [3] |
RICHTER H, SIMON D. Robust tracking control of a prosthesis test robot[J]. Journal of dynamic systems, measurement, and control, 2014, 136(3): 031011. DOI:10.1115/1.4026342 (  0) 0) |
| [4] |
GOLDFARB M, BARTH E J, GOGOLA M A, et al. Design and energetic characterization of a liquid-propellant-powered actuator for self-powered robots[J]. IEEE/ASME transactions on mechatronics, 2003, 8(2): 254-262. DOI:10.1109/TMECH.2003.812842 (  0) 0) |
| [5] |
SUP F, BOHARA A, GOLDFARB M. Design and control of a powered knee and ankle prosthesis[C]//IEEE International Conference on Robotics and Automation. Roma, 2007: 4134-4139.
(  0) 0) |
| [6] |
JIN D W, YANG J K, ZHANG R H, et al. Terrain identification for prosthetic knees based on electromyographic signal features[J]. Tsinghua science and technology, 2006, 11(1): 74-79. DOI:10.1016/S1007-0214(06)70157-2 (  0) 0) |
| [7] |
谭冠政, 蔡光超, 曾庆冬, 等. CIP-I智能仿生人工腿手持控制系统研究与设计[J]. 计算机测量与控制, 2006, 14(1): 47-50. (  0) 0) |
| [8] |
耿艳利, 杨鹏, 许晓云, 等. 动力型假肢膝关节设计与仿真研究[J]. 河北工业大学学报, 2011, 40(5): 1-4. DOI:10.3969/j.issn.1007-2373.2011.05.001 (  0) 0) |
| [9] |
韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2008.
(  0) 0) |
| [10] |
HAN J. From PID to active disturbance rejection control[J]. IEEE transactions on industrial electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 (  0) 0) |
| [11] |
韩京清. 自抗扰控制技术[J]. 前沿科学, 2007, 1(1): 24-31. DOI:10.3969/j.issn.1673-8128.2007.01.004 (  0) 0) |
| [12] |
SUP F, VAROL H A, MITCHELL J, et al. Preliminary evaluations of a self-contained anthropomorphic transfemoral prosthesis[J]. IEEE/ASME transactions on mechatronics, 2009, 14(6): 667-676. DOI:10.1109/TMECH.2009.2032688 (  0) 0) |
| [13] |
蔡自兴, 谢斌. 机器人学[M]. 北京: 清华大学出版社, 2015.
(  0) 0) |
| [14] |
WINTER D A. Biomechanics and motor control of human movement[M]. New York: John Wiley & Sons Inc, 2009.
(  0) 0) |
| [15] |
GB/T 10000—1988中国成年人人体尺寸[S].中国标准出版社, 1988.
(  0) 0) |
| [16] |
GB/T 17245—2004成年人人体惯性参数[S].中国标准出版社, 2004.
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


