2. 广西云安全与云服务工程技术研究中心 广西壮族自治区 桂林 541004
2. Guangxi Cloud Security and Cloud Service Engineering Technology Research Center, Guilin 541004, China
在我国,随着市民公共交通出行需求逐渐增加,轨道交通成为市民重要的出行方式。准确的轨道交通客流预测有助于公共安全和车辆调度,对智慧交通的发展有着重要意义。本文的目标是根据轨道交通站点历史刷卡数据提供准确的站点客流量短期预测。在轨道交通网络中,站点刷卡设备记录的乘客刷卡数据可以生成交通时间序列数据和地理信息,为轨道交通预测提供了丰富的数据。早期,研究人员使用时序分析模型解决轨道交通客流量预测问题,但这些模型很难处理动态的非线性数据。后来,研究人员采用机器学习对客流量进行预测,但是仍然难以同时考虑高维交通数据的时空相关性。由于轨道交通客流有着复杂的时空相关性以及较大的波动性,采用传统的机器学习算法实现轨道交通客流预测有较大的难度。近年来,研究者采用深度学习方法来处理高维时空数据,即采用卷积神经网络(convolutional neural network,CNN)有效提取网格数据的空间特征[1]或采用图卷积神经网络(graph convolutional neural network,GCN)描述基于图的数据空间相关性[2]。然而,这些方法仍然不能同时对交通数据的时空特征和动态相关性进行建模。
针对上述问题,本文提出了一种基于注意力机制和多图视角图神经网络的轨道交通客流预测模型(multi-graph convolutional neural network for spatial and temporal attention,MGCNSTA)。该模型可以直接在原始的基于图形的交通网络上处理交通数据,有效地捕捉动态时空特征。本文的主要贡献有:设计了一种基于邻接图和出发地-目的地(OD)图的多图视角模型,用于建模交通数据的时空相关性;设计了一种时空注意力机制和时空卷积模型来捕获轨道交通数据的动态时空相关性,该模型使用空间注意力机制以及图卷积模块捕获不同站点间动态的空间关系,并使用时间注意力机制以及时间卷积模块捕捉不同时间之间的动态时间相关性;使用真实地铁刷卡交通数据集进行大量实验,验证了本文的模型优于基线方法。
1 相关工作对于轨道交通的客流量预测,当前研究方法主要有下面几种。
1) 统计模型及线性方法。在交通流量预测领域,早期研究人员提出了许多统计学方法和线性模型来预测交通流量。如动态线性方法[3]、自回归移动平均(auto-regressive moving average, ARMA)预测模型[4]、基于概率树的客运量模型[5]、卡尔曼滤波方法[6]等。由于客流具有显著的非线性特征,这些方法对于复杂的交通流量预测效果不佳。
2) 非线性模型及机器学习方法。研究人员根据交通流量的非线性特征建立了如小波分析和SVM相结合的模型[7]、BP(back propagation)神经网络[8]等方法对交通流量进行预测。然而,这些传统的机器学习方法需要特征工程的支持,将原始数据转换为合适的内部特征以匹配模型。同时,轨道交通客流预测的重要特征是时空相关性[9],但通过特征工程难以建立时空相关性的特征。
3) 深度学习方法及多模型融合方法。随着传感技术的发展,人们可通过交通监控设备获取大量的交通信息化数据,这便促成研究人员使用深度学习或多模型融合的方法对交通流量进行预测。有学者采用LSTM(long-short term memory)及其改进方法[10]来对交通流量进行预测。这些模型比传统机器学习的预测方法具有更好的准确性,但LSTM无法捕获空间相关性信息导致其预测效果有限。有研究人员采用CNN构建二维网格的形式描述路网进行建模。但这种方法未考虑道路网络的拓扑依赖关系。对于轨道交通这种图结构网络,采用GCN或GCN的改进方法挖掘图结构的空间相关性可取得更好的效果[11]。还有一些研究人员创建基于时空相关性的STGCN[12]、ASTGCN[13]、STFGNN[14]、MCSTGCN[15]、FC-LSTM[16]、CVSTGCN[17]等混合模型来预测公共交通流量。STGCN可以有效地捕捉道路网络空间结构的相关性。ASTGCN是在STGCN的基础上增加了注意力机制,并且加上周、日和近期三个时间段的信息输入,能够更好地捕获到交通网络流量中时间和空间信息,从而达到较好的预测效果。而STFGNN则提出了时空图的概念,把时间维度和空间维度的信息结合在一起,能够使模型捕获到更直观的时空信息。但以上模型大都运用在道路车流量网络,而在轨道交通客流预测上的研究甚少。并且ASTGCN模型过于庞大,而STFGNN虽然结合了近期的时间维度,但未彻底解决无法学习长期时间维度上的问题。CVSTGCN结合坐标方法来指定不同特征信息在不同时空维度上的影响程度,通过图卷积网络来指定不同时空维度的时空信息。
本文提出的MGCNSTA针对轨道交通的时间空间相关性特征以及刷卡数据产生的OD图视角,运用基于注意力机制和多图视角的卷积神经网络对轨道交通客流数据预测进行建模。
2 模型设计 2.1 变量定义轨道交通网络由站点通过对应的线路连接组成。本文用符号G表示轨道交通站点形成的网络,定义G=(V, E),其中:V表示轨道交通网络中的站点集合,|V|=N,N表示轨道交通网络中站点的个数,v∈V为网络中的一个站点;E表示轨道交通网络中的边集,即站点间相连接的线路。用四元组Tkt(k, t, p, v)表示乘客p在t时刻从站点v进站或出站的记录,k为进站或出站标志。用t=[tstart, tend)表示某个时间区间,则在时间区间t内,可根据站点生成的进站、出站记录计算站点上产生的进站、出站流量,进站和出站流量的计算公式为
| $ \begin{aligned} & x_v^{\mathrm{in}, t}=count\left(\left\{T \mid T . k=x_{\mathrm{in}}\right.\right. \text { and } \\ & T . v=v \text { and } T . \tau \in t\}), \end{aligned} $ | (1) |
| $ \begin{aligned} & x_v^{\text {out }, t}=count\left(\left\{T \mid T . k=x_{\text {out }}\right.\right. \text { and } \\ & T . v=v \text { and } T . \tau \in t\}), \end{aligned} $ | (2) |
其中:xin、xout分别为进站、出站客流量;τ为当前时刻表示。
计算轨道交通站点一段时间的总体客流量时,用Fvt表示在时间区间t内站点v的总客流量大小,Fvt的计算公式为
| $ F_v^t=x_t^{\mathrm{in}, v}+x_t^{\text {out }, v} 。$ | (3) |
图 1展示了本文提出的MGCNSTA模型总体框架,其中
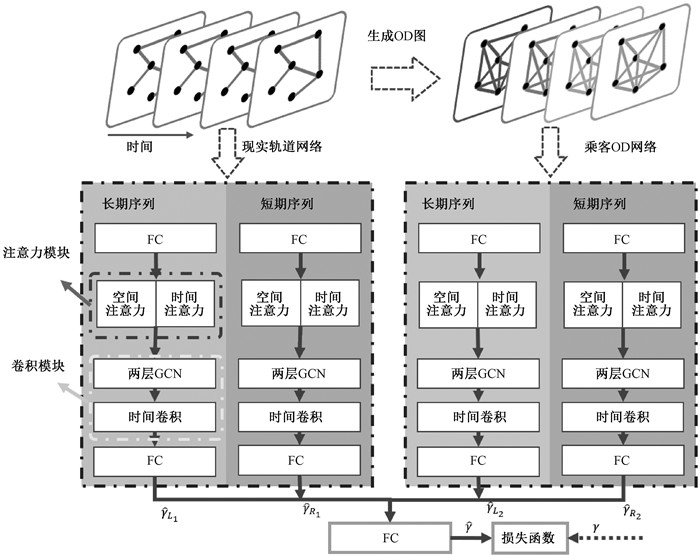
|
图 1 MGCNSTA模型总体架构 Fig. 1 MGCNSTA general framework |
1) 站点网络连接和OD网络连接。轨道交通网络有固定的运行路线和站点,乘客的出行活动与站点位置、运行路线的分布有相关性。同时,轨道交通实行的是“一程一票”方式,对于一个完整正常的乘坐活动,包含一次进站和一次出站。因此由乘客出发地-目的地路径构成的OD网络图也与客流量有相关性。本文分别用站点邻接矩阵和t时间区间内的OD矩阵表示站点图数据和OD图数据。在t时间区间内,乘客p的一次乘坐记录进站点i到出站点j表示为边eijp。所有该段时间内乘客的乘坐记录构成OD图,表示为GOD=(V, EODt),其中EODt为t时间内所有eijp的集合。轨道交通网络中站点个数为N邻接矩阵Aadj=[aij]N×N,构建如式(4),OD矩阵AOD=[aijOD]N×N,aij、aijOD构建式为
| $ a_{i j}= \begin{cases}1, & e_{v_i v_j} \in E, \\ 0, & \text { 其他 , }\end{cases} $ | (4) |
| $ a_{i j}^{O D}= \begin{cases}\ln \left(count\left(e_{i j}^p\right)\right), & e_{i j}^p \in E_{O D}^t, \\ 0, & \text { 其他。}\end{cases} $ | (5) |
取该时间段内乘坐i至j的所有乘客的乘坐记录数之和再取对数,这是为了避免OD图边的权值有较大的差值。
2) 长期序列和短期序列。轨道交通网络具有长期时间和短期时间的时间相关性。为了捕获数据长期序列与短期序列的周期特征,本文设置了长期与短期两种序列采样方式。假设采样频率为每天n次,当前时间为t0,待预测时间段为Wf,本文按照时间序列截取M和L两种长度的时间序列片段,分别作为短期和长期分量的输入,均为Wf的整数倍。短期分量为连续序列,其输入的截取为
| $ \boldsymbol{X}_M=\left(\boldsymbol{X}_{t_0-M+1}, \boldsymbol{X}_{t_0-M+2}, \cdots, \boldsymbol{X}_{t_0}\right) \in \mathbf{R}^{N \times R} \text { 。} $ | (6) |
长期分量为离散序列,其输入的截取公式为
| $ \begin{aligned} & \boldsymbol{X}_L=\left(x_{t_0-\left(L / W_f\right) * n+1}, \cdots, x_{t_0-\left(L / W_f\right) * n+W_f}, \cdots, \right. \\ & x_{t_0-\left(L / W_f-1\right) * n+1}, \cdots, x_{t_0-\left(L / W_f-1\right) * n+W_f}, \cdots, \\ & \left.x_{t_0-n+1}, \cdots, x_{t_0-n+W_f}\right) \in \mathbf{R}^{N \times L} 。\end{aligned} $ | (7) |
3) 注意力机制模块。在轨道交通网络中站点在不同的时间片段下相关性是不一样的,例如在上下班高峰时期,商业区、工业区和住宅区的站点客流量会有明显增高。因此在不同的时间片段下对所计算站点的客流量影响也是动态变化的。本文运用注意力机制动态捕获站点在不同时间下当前相关性较大的关键特征。空间和时间注意力矩阵计算公式分别为
| $ \boldsymbol{S}_A=\operatorname{Softmax}\left(\left(\boldsymbol{W}_K^1 \boldsymbol{X}_v\right)^{\mathrm{T}} \cdot \boldsymbol{W}_Q^1 \boldsymbol{X}_v\right) \cdot \boldsymbol{W}_V^1 \boldsymbol{X}_v, $ | (8) |
| $ \boldsymbol{T}_A=\operatorname{Softmax}\left(\left(\boldsymbol{W}_K^2 \boldsymbol{X}_t\right)^{\mathrm{T}} \cdot \boldsymbol{W}_Q^2 \boldsymbol{X}_t\right) \cdot \boldsymbol{W}_V^2 \boldsymbol{X}_t, $ | (9) |
其中:WK1,WQ1,WV1∈ RN×N,WK2,WQ2,WV2∈ RN×1皆为可学习参数矩阵,其作用是学习到轨道交通网络中各个站点在各个时间片段下的权值大小;X =(x1, x2, …, xα)∈ RN×α为全连接(fully connected,FC)层输出,α为FC输出时间维度,而Xv和 Xt分别为以节点和以时间切分的数据。式(8)的空间注意力机制是计算各个节点间的特征相关性,式(9)是计算各个时间片段特征的相关性。此处的注意力机制的计算参考了Transformer中的自注意力机制的计算[18]。SA中的元素表示轨道交通站点的空间维度权重,TA中的元素大小表示轨道交通站点的时间维度权重。经过注意力机制模块后输出为
| $ \hat{\boldsymbol{X}}=\boldsymbol{S}_A \odot \boldsymbol{X} \odot \boldsymbol{T}_A, $ | (10) |
将原数据 X 经 SA和 TA加权后得到
4) 卷积模块。卷积模块分为图卷积单元和时间卷积单元。图卷积单元由两层GCN网络组成。图卷积单元包括基于邻居图的时空捕获模块和基于OD图的时空捕获模块。用
| $ \tilde{\boldsymbol{x}}_N^{(l)}=\operatorname{ReLU}\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_N^{(l)} *{ }_{G_N} \tilde{x}_N^{(l)}\right) \in \mathbf{R}^{T_N^{(l)} \times N}, $ | (11) |
| $ \tilde{\boldsymbol{x}}_{\mathrm{OD}}^{(l)}=\operatorname{ReLU}\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\mathrm{OD}}^{(l)} *{ }_{G_{\mathrm{OD}}} \tilde{x}_{\mathrm{OD}}^{(t)}\right) \in \mathbf{R}^{T_{\mathrm{OD}}^{(l)} \times N} 。$ | (12) |
在数据经过GCN计算后进入时间卷积单元,时间卷积单元使用卷积神经网络,输入为TN(l)×N的矩阵,而时间卷积单元卷积核维度为1×TN(l)的CNN卷积核。时间卷积单元通过相邻时间片的节点更新当前节点的信号,计算公式
| $ \ddot{\boldsymbol{x}}=\operatorname{ReLU}\left(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^* \tilde{\boldsymbol{x}}\right)。$ | (13) |
其中:Φ为卷积核;*为卷积操作。
经过卷积模块后进入FC调整,分别得到数值
| $ \hat{\gamma}=\operatorname{ReLU}\left(f\left(\hat{\gamma}_{L_1}, \hat{\gamma}_{R_2}, \hat{\gamma}_{L_2}, \hat{\gamma}_{R_2}\right)\right)。$ | (14) |
本文模型训练首先根据地铁站点连接关系构建邻接矩阵,根据时间区间内乘客进站、出站记录构建OD矩阵,随后设定每个样本的输入序列长度和预测窗口长度,采用滑动窗口的方法依次向前滑动训练窗口和预测窗口,构建训练、验证和测试数据集,接着使用训练集对模型进行训练。在模型训练过程中,采用均方误差损失函数(mean squared error loss function,MSE)作为损失函数,采用Adam作为优化器,最后得到训练完成的MGCNSTA模型。当使用训练完成的模型进行流量预测时,直接将测试样本以及交通站点邻接矩阵输入到模型中,即可得到预测的流量值。模型训练的步骤如算法1所示。
算法1 MGCNSTA模型训练算法
输入:轨道交通历史流量序列X ={ XR, XL}, 站点邻接矩阵Aadj,站点OD矩阵AOD, 输出的时间序列长度Wf, batch_size, epochs。
输出:训练完成后的模型以及模型参数。
01) For i=1 to n-Tin-Tout+1 {
02) xi=(XRi, XLi);
03) yi=(Xi+1, Xi+2, …, Xi+Wf);
04) Data_tarinadd (Xi, yi);
05) }
06) 初始化模型net;
07) While epochs! =0 {
08) Data_batch=Data_train[batch_size];
09) OD_graph_module(Data_batch.xi){
10)
11)
12) };
13) Station_graph_module(Data_batch.xi){
14)
15)
16) };
17)
18) 计算训练输出和真实值误差;
19) 反向传播更新模型参数;
20) epochs=epochs-1;
21) }
3 实验验证 3.1 实验环境和参数设置本文实验所用计算机CPU为AMD 2700,GPU为GTX1080,内存容量64 GB,操作系统为window 10。实验使用Pytorch框架搭建模型。
采用杭州地铁轨道交通数据集验证本文模型。该数据集由乘客进站、出站刷卡记录数据生成的。轨道交通网络包含81个站点,包括2019年1月1日至26日共六千五百多万条刷卡数据。由于夜间地铁不运行,不产生流量,因此只选取6:00—23:59的数据,并通过线性插值法补全空缺值。实验每隔10 min截取计算客流量,因此设置时间步长为10 min。选取数据的80%作为训练集,10%作为验证集,10%作为测试集进行实验。
在训练中,MGCNSTA模型中时间卷积层的卷积核时间维度为2,参数设置如表 1所示。
|
|
表 1 MGCNSTA模型训练参数设置 Tab. 1 MGCNSTA training parameter setting |
本文实验选取均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)评估模型优劣,其计算公式分别为
| $ RMSE=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}, $ | (15) |
| $ MAE=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left|\hat{y}_i-y_i\right|} 。$ | (16) |
采用GCN、TGCN[2]、GRU、Chebnet、LSTM[10]和ASTGCN[13]作为基线模型来对比预测结果。
各模型的输入序列总长度与MGCNSTA一致,在预测时间步长为6时,即预测一个小时各个站点的客流,各模型预测结果如表 2所示。实验表明MGCNSTA相对于基线模型中表现最优的ASTGCN, 在MAE上有15.06%的改进,在RMSE上有20.05%的改进。本文所使用的数据集为真实的轨道交通数据集,预测难度较高,其预测难度主要体现在模型不仅要考虑时间和流量的相关性,而且要考虑到站点连接上的空间相关性。同时,数据由人的刷卡行为产生,人的乘坐意愿即源和目的地的空间相关性也需要被考虑。轨道交通客流量存在短时间的高峰时期和低谷时期,并且高峰时期和低谷时期的流量差距较大,每日的流量波动也受天气、节假日、政策等影响,这也是轨道交通与普通路网交通的流量预测差别。而GCN、Chebnet只关注了空间结构的信息,因此效果较差。GCN相对Chebnet可学习参数较少,没有学习到更多的空间信息。而GRU和LSTM同为RNN模型,LSTM能够捕获长时间信息的效果更好。TGCN由于不能对局部流量的变化精准预测,即TGCN输出效果更为平滑,不能准确预测轨道交通实际的波动较大的客流变化,导致整体的预测效果较差。ASTGCN是交通流量预测的优秀模型,优于其他基线模型。但其对数据要求较高,在本文数据集中,仅有26天的数据,可用于训练的数据只用20天。在这种小规模的数据上,ASTGCN并不能很好地发挥作用。并且因为ASTGCN没有考虑到轨道交通站点与乘客源和目的地的特殊性。本文方法MGCNSTA能够捕获到时间空间信息,并且结合了注意力机制,选取长期序列和短期序列输入模型,并且考虑乘客的源和目的地的空间相关性构建OD图视角进行学习,因此在所有模型中,预测结果是最优的。
|
|
表 2 与基线模型预测效果对比 Tab. 2 Compared with baseline model |
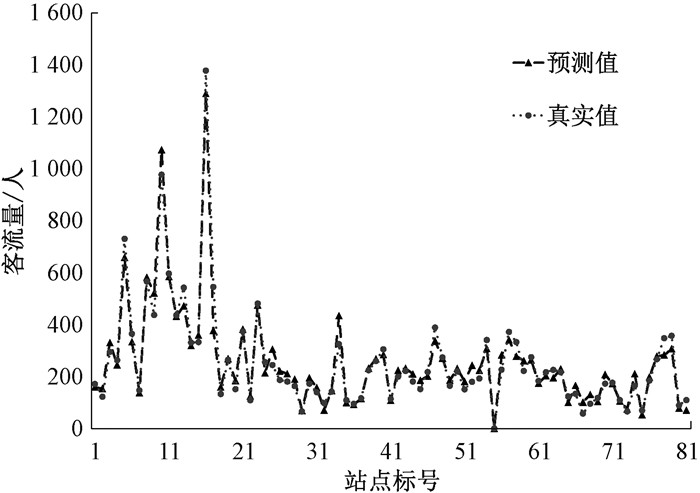
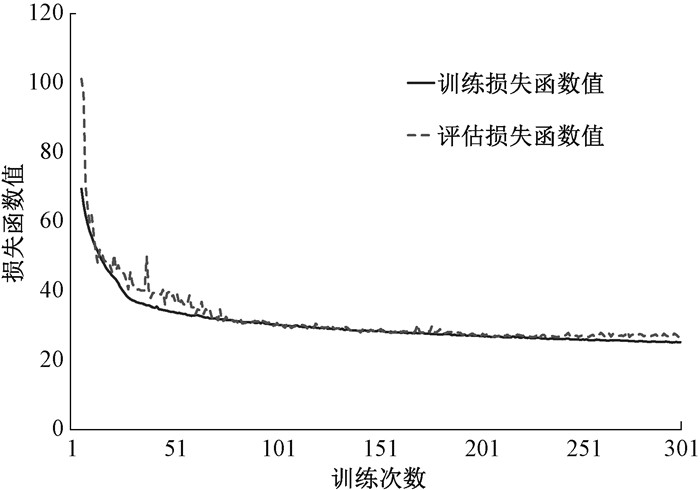
图 2为MGCNSTA模型的预测值和真实值的对比,选取的测试数据为测试集中随机一个预测时间片。实验表明MGCNSTA不仅能够学习流量的趋势,在局部变化较大时,也能够准确预测。图 3为训练损失值和评估损失值下降比较,在300个epoch前模型已经收敛。
|
图 2 MGCNSTA预测值与真实值的可视化 Fig. 2 Visualization of MGCNSTA predicted value and real value |
|
图 3 MGCNSTA训练损失函数值和评估损失函数值对比 Fig. 3 MGCNSTA training loss function value and evaluation loss function value comparison |
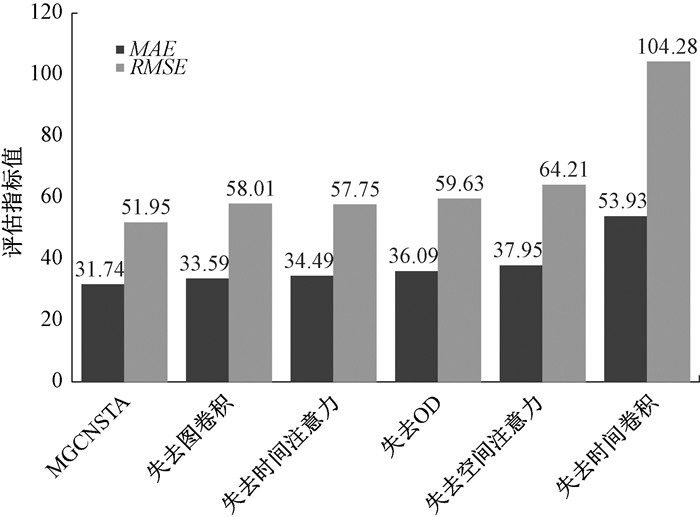
此外,本文还做了MGCNSTA的消融实验,实验输入、输出与前文实验一致,实验结果如图 4所示。对于流量预测的任务,本质上仍然是时间序列的预测。因此在消融实验中,MGCNSTA模型发挥最大作用的是时间卷积模块,时间卷积模块能够学习到站点在时间维度的相关性。空间注意力在MGCN中也发挥了重要作用,这是因为在轨道交通中,如果只运用图卷积神经网络去捕获空间信息会忽略掉轨道交通本身的轨道线路的物理条件。虽然有换乘站点能够使不同线路的乘客任意搭乘,但是在列车运行时,通过站点换乘的乘客数量是要少于列车行进方向的站点下车的乘客。因此,通过注意力机制能够让模型学习不同站点的空间相关性。而OD图则是能让模型学习乘客在不同时间下源和目的地的相关性,即跨物理连接的站点空间相关性。这对于轨道交通来说是十分重要的。在普通路网下,不存在固定的站点,也不存在固定站点连接路线,无法为OD图建模。而轨道交通数据可建立OD图,因此能够使用OD图让模型学习更多的隐含信息,显著提升了预测结果。实验表明MGCNSTA的各个模块都发挥了不可或缺的作用,各个模块的结合使得MGCNSTA在轨道交通流量预测上有优秀的效果。
|
图 4 MGCNSTA消融实验 Fig. 4 MGCNSTA ablation experiment |
本文设计了一种时空注意力机制和时空卷积模型来捕获轨道交通数据的动态时空相关性。该模型的空间注意力机制以及图卷积模块用于捕获不同站点间动态的空间关系。时间注意力机制以及时间卷积模块用于捕捉不同时间之间的动态时间相关性。并且该模型基于邻接图和OD图多图视角的图卷积模型,用于建模交通数据的时空相关性。本文使用杭州地铁刷卡交通数据集进行大量实验,验证了本文的模型与基线方法相比具有较优结果。目前本文模型在适用性上有待改进,并且未来考虑强化轨道交通线路的时空信息捕获,在更多的轨道数据集上进行验证。
| [1] |
MA X L, DAI Z, HE Z B, et al. Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors (Basel, Switzerland), 2017, 17(4): 818. DOI:10.3390/s17040818 (  0) 0) |
| [2] |
ZHAO L, SONG Y J, ZHANG C, et al. T-GCN: a temporal graph convolutional network for traffic prediction[J]. IEEE transactions on intelligent transportation systems, 2020, 21(9): 3848-3858. DOI:10.1109/TITS.2019.2935152 (  0) 0) |
| [3] |
FEI X, LU C C, LIU K. A Bayesian dynamic linear model approach for real-time short-term freeway travel time prediction[J]. Transportation research part C: emerging technologies, 2011, 19(6): 1306-1318. DOI:10.1016/j.trc.2010.10.005 (  0) 0) |
| [4] |
CAO L, LIU S G, ZENG X H, et al. Passenger flow prediction based on particle filter optimization[J]. Applied mechanics and materials, 2013, 373/374/375: 1256-1260. (  0) 0) |
| [5] |
LENG B, ZENG J B, XIONG Z, et al. Probability tree based passenger flow prediction and its application to the Beijing subway system[J]. Frontiers of computer science, 2013, 7(2): 195-203. DOI:10.1007/s11704-013-2057-y (  0) 0) |
| [6] |
JIAO P P, LI R M, SUN T, et al. Three revised Kalman filtering models for short-term rail transit passenger flow prediction[J]. Mathematical problems in engineering, 2016, 2016: 9717582. (  0) 0) |
| [7] |
SUN Y X, LENG B, GUAN W. A novel wavelet-SVM short-time passenger flow prediction in Beijing subway system[J]. Neurocomputing, 2015, 166: 109-121. DOI:10.1016/j.neucom.2015.03.085 (  0) 0) |
| [8] |
LI Q, QIN Y, WANG Z Y, et al. The research of urban rail transit sectional passenger flow prediction method[J]. Journal of intelligent learning systems and applications, 2013, 5(4): 227-231. DOI:10.4236/jilsa.2013.54026 (  0) 0) |
| [9] |
CHEN J, PEI T, SHAW S L, et al. Fine-grained prediction of urban population using mobile phone location data[J]. International journal of geographical information science, 2018, 32(9): 1770-1786. DOI:10.1080/13658816.2018.1460753 (  0) 0) |
| [10] |
LIU Y, LIU Z Y, JIA R. DeepPF: a deep learning based architecture for metro passenger flow prediction[J]. Transportation research part C: emerging technologies, 2019, 101: 18-34. DOI:10.1016/j.trc.2019.01.027 (  0) 0) |
| [11] |
刘玉强, 顾晶晶, 孙明, 等. 基于城市区域多模态融合的人群流量预测[J]. 郑州大学学报(理学版), 2022, 54(1): 25-31. LIU Y Q, GU J J, SUN M, et al. Exploring the multimodal fusion of urban regions for crowd flow prediction[J]. Journal of Zhengzhou university (natural science edition), 2022, 54(1): 25-31. (  0) 0) |
| [12] |
YU B, YIN H T, ZHU Z X. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting[C]//Proceedings of the 27th International Joint Conference on Artificial Intelligence. Piscataway: IEEE Press, 2018: 3634-3640.
(  0) 0) |
| [13] |
GUO S N, LIN Y F, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Menlo Park: AAAI Press, 2019: 922-929.
(  0) 0) |
| [14] |
LI M Z, ZHU Z X. Spatial-temporal fusion graph neural networks for traffic flow forecasting[EB/OL]. (2020-12-15)[2022-03-12]. https://arxiv.org/pdf/2012.09641.
(  0) 0) |
| [15] |
冯宁, 郭晟楠, 宋超, 等. 面向交通流量预测的多组件时空图卷积网络[J]. 软件学报, 2019, 30(3): 759-769. FENG N, GUO S N, SONG C, et al. Multi-component spatial-temporal graph convolution networks for traffic flow forecasting[J]. Journal of software, 2019, 30(3): 759-769. (  0) 0) |
| [16] |
SHUAI C Y, WANG W C, XU G, et al. Short-term traffic flow prediction of expressway considering spatial influences[J]. Journal of transportation engineering, 2022, 148(6): 4022026. DOI:10.1061/JTEPBS.0000660 (  0) 0) |
| [17] |
LI M, LI M S, LIU B L, et al. Spatio-temporal traffic flow prediction based on coordinated attention[J]. Sustainability, 2022, 14(12): 7394. DOI:10.3390/su14127394 (  0) 0) |
 2023, Vol. 55
2023, Vol. 55

