2. 中国海洋大学 信息科学与工程学院 山东 青岛 266100
2. College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China
海洋物联网广泛应用于海洋学等领域,例如海洋数据收集、环境监测、资源勘探和海军军事[1].在这些应用中,收集的数据必须与位置信息匹配[2-3].因此,研究海洋物联网定位具有重要现实意义.
近年来,海洋物联网定位技术发展日渐成熟[4],但是与陆地物联网定位技术相比,依然存在着较大差距[5].陆地物联网定位通过全球定位系统(global positioning system,GPS)或者是直接定位方法快速实现节点定位,GPS技术得到了广泛应用[6].但在海洋物联网水下环境中,主要通过声波进行通信,声波在水中传播速度受到多种因素的影响,例如:发射信号的功率低、噪声大、信号能量衰减快以及信道的冲激响应等[7].
水下信号的传播介质与陆地上的传播介质相差较大,GPS信号会迅速衰减,以至于无法定位[8-9].并且海洋物联网中的节点位置会随着海流移动而变化,从而增加了水下节点定位的误差[10].因此,陆地定位技术不能直接应用于海洋物联网,并且后者因很多限制因素而难以实现.目前,陆地物联网定位技术一般分两种:基于距离的定位算法(range-based)和距离无关的定位算法(range-free)[11-12].range-based主要依据相邻节点间的精确距离计算来测量节点的位置.包括多种算法机制,如:到达时间(time of arrival,TOA)、到达角度(angle of arrival,AoA)[13]、接收信号强度(received signal strength indicator,RSSI)[14]等.range-free不需要精确的节点位置即可定位.很多算法采用了这种技术,如:质心算法[15]、距离向量-跳段算法(distance vector-hop,DV-Hop)[16].由于水下和陆地环境的差异,这些方法不能用于海洋物联网.
大多数基于距离的定位算法都需要高精度的时间同步算法.其中,多跳拟合定位方法(multihops fitting localization approach,MFLA)[17]用于定位孤立未知节点.此算法中使用的中间节点设置为路由器,通过贪婪方法构建路径,多跳路径近似描述为直线,通过三边定位方程来计算未知节点位置.Cheng等[18]提出了一种不需要时间同步的定位方案,这种大规模定位(localization scheme for large scale underwater networks,LSLS)采用到达时间差异方法测量不同传感器的距离,LSLS算法应用于大规模水下网络定位.
距离无关的定位算法仅提供节点位置的模糊估计.Hu等[19]介绍了蒙特卡洛定位方法, 可以在节点的移动性不可控制的情况下,改善节点定位的精度和准确度.一些研究人员使用无人机进行海洋定位,多直升机协同网络物理系统是一种无人驾驶四轴飞行器的网络物理系统,进行空气污染源的定位.在该系统中,采用了GPS定位,为系统提供连续和精确的定位信息,四轴飞行器需要布置大量传感器定位污染源,通过射频方式将所得信息返回到基站.然而射频信号在水下传输距离较短,并且传感器节点布置困难,此系统很难直接应用于水下节点定位[20].
虽然这些算法涉及了在静动态海洋环境中,信标节点部署以及水下节点定位的问题,但都没有同时考虑多信源节点静动态定位以及速度对单信标节点移动的影响等问题,从而无法在不同的海洋环境中精确部署节点,不能达到准确定位.为解决上述问题,基于海洋物联网的特点,本文提出了一种新的多信源海洋物联网定位算法.该算法包括多信源静态定位算法MSL和多信源动态定位算法MDL.该算法解决了信标节点难以准确部署的问题,节约了定位成本.同时,由于定位过程中,没有辅助节点的参与,大大缩短了定位时间,减少了定位误差.除此之外,本文算法较之前算法,更好地解决了当前海洋物联网定位的问题.
本文的贡献主要是3个方面:1)基于多信源海洋物联网的特点,将位置精确的岸边建筑物、海面舰船和航标等作为信标节点辅助定位,减少了定位过程所需要信标节点的数量(多信源静态定位算法:近海海域需要的信标节点的数量为4个,远海海域需要的信标节点数量为2个;多信源动态定位算法中需要的信标节点的数量仅为1个).2)分析了海洋物联网节点定位的基本原理,并说明了信标节点与水下待定位节点之间的通信过程,设计了针对不同海洋环境的多源定位算法.3)与其他定位算法进行仿真比较,通过仿真结果,总结分析了不同海洋环境下MSL算法和MDL算法的性能.
1 算法设计为了实现水下目标位置和轨迹的精确预判,需要利用信标节点来进行辅助定位.但是在实际部署过程中,由于受到海域外在条件限制,信标节点的部署工作难以顺利进行.在海洋物联网中,岸边基站、建筑物以及海面船舶等具有精确位置的物体可作为信标节点来辅助定位.本节设计了多信源海洋物联网定位算法用于水下静态、动态节点定位.
1.1 多信源静态节点定位算法本节设计了多信源静态节点定位算法MSL,用于水下待定位节点定位过程中保持静止的情况.
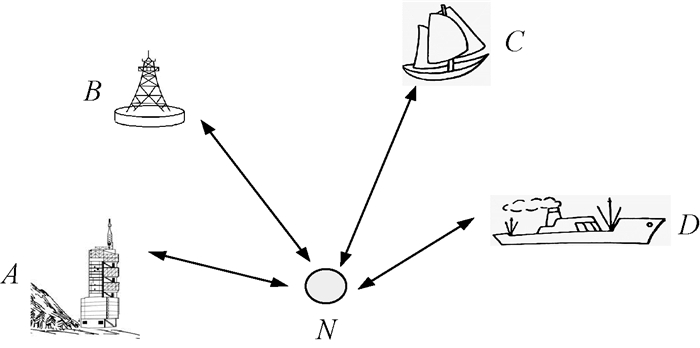
图 1标明了信标节点和水下待定位节点的分类,岸边建筑物A、浮标B、海面帆船C、轮船D作为信标节点,这类信标节点可以利用携带的定位装置时刻确定自身位置,节点N作为水下待定位节点.水下待定位节点N以广播形式发出定位请求信息,信标节点在收到水下待定位节点N的请求定位信息后,采用TOA测距方法计算出其与水下待定位节点N之间的距离,具体公式为
| $ {d_{i, N}} = c \times {t_{i, N}}, $ | (1) |
|
图 1 近海多信源静态节点定位图 Fig. 1 Multi-source static node localization in the offshore area |
其中:c为节点之间通信的水下声波速度;ti, N为节点之间通信时间;i=A, B, C, D.
信标节点和水下待定位节点通信过程中水下声波速度公式[21]为
| $ \begin{array}{l} c = 1449.\;30 + 4.\;6T - 0.\;055{T^2} + 0.000\;29{T^3} + \\ \left( {1.\;34 - 0.\;010T} \right) \times \left( {S - 35} \right) + 0.\;168P, \end{array} $ | (2) |
其中:T表示节点所在海域水下温度;S代表节点所在海域海水盐度;P为节点在海域水下位置的压强.
信标节点返回自身位置信息和它们与水下待定位节点N之间的距离.水下待定位节点N收到信标节点返回的信息,利用多边定位原理,得到多边距离公式
| $ \left\{ {\begin{array}{*{20}{c}} {{{\left( {{x_A} - {x_N}} \right)}^2} + {{\left( {{y_A} - {y_N}} \right)}^2} + {{\left( {{z_A} - {z_N}} \right)}^2} = d_{AN}^2}\\ {{{\left( {{x_B} - {x_N}} \right)}^2} + {{\left( {{y_B} - {y_N}} \right)}^2} + {{\left( {{z_B} - {z_N}} \right)}^2} = d_{BN}^2}\\ {{{\left( {{x_C} - {x_N}} \right)}^2} + {{\left( {{y_C} - {y_N}} \right)}^2} + {{\left( {{z_C} - {z_N}} \right)}^2} = d_{CN}^2}\\ {{{\left( {{x_D} - {x_N}} \right)}^2} + {{\left( {{y_D} - {y_N}} \right)}^2} + {{\left( {{z_D} - {z_N}} \right)}^2} = d_{DN}^2} \end{array}} \right. $ | (3) |
其中:(xA, yA, zA)、(xB, yB, zB)、(xC, yC, zC)和(xD, yD, zD)分别是岸边建筑物A、浮标B、海面帆船C和轮船D的坐标;(xN, yN, zN)表示水下待定位节点N坐标;dAN、dBN、dCN、dDN分别是岸边建筑物A、浮标B、海面帆船C和轮船D与水下待定位节点N之间的距离.根据多边公式(3)可以求得水下待定位节点N的坐标.MSL算法精度高、计算量小,但是在定位过程中,至少需要4个信标节点.
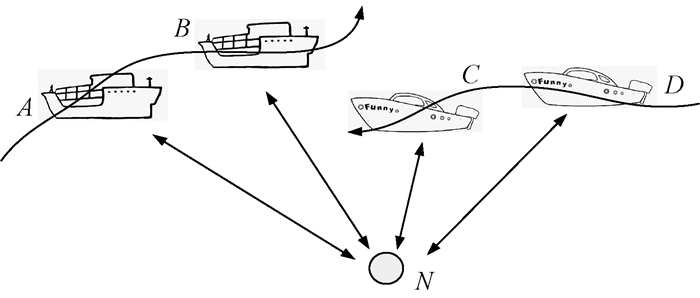
在远海,舰船、航标、建筑物等分布相对稀疏,造成信标节点数目有限,当返回的位置信息数目不能达到使用定位算法中信标节点数目下限时,水下待定位节点利用与移动的船舶多次通信完成位置坐标的计算.图 2展现了这一过程.水下待定位节点N利用公式(3)计算得到位置.
|
图 2 远海多信源静态节点定位图 Fig. 2 Multi-source static node localization in the remote sea |
MSL算法定位过程如下.
|
|
通常,水下节点在洋流等的影响下会随水流移动,这样就造成了作为信标节点的船舶和水下待定位节点位置会随着时间的变化而改变.在近海海域,分布着充足的信标节点,水下待定位节点发送一次定位请求信息,就可以得到充足定位信息.节点的移动不会影响最终算法性能.在远海,信标节点数目不足,水下待定位节点收到定位信息不会达到定位需求,这就会给节点定位带来影响.
1.2 多信源动态节点定位算法由于水下待定节点得到定位请求回复位置不是固定的,直接利用静态定位算法对水下待定位节点进行位置的计算会带来较大误差.为了解决上述问题,本节设计了多信源动态节点定位算法MDL.
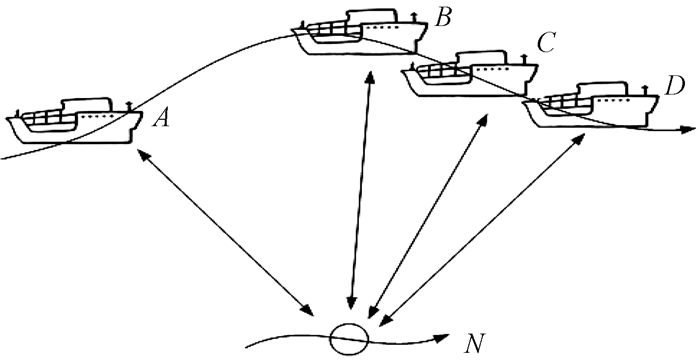
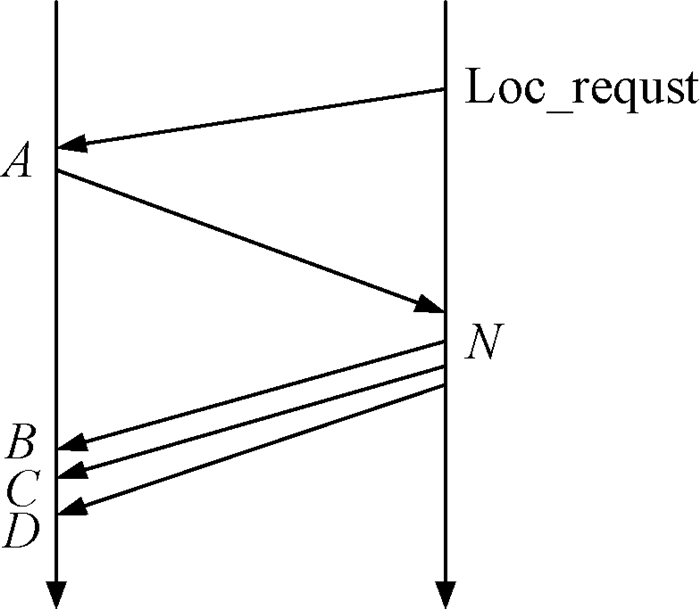
如图 3所示,水下待定位节点N广播定位请求信息,船舶在位置A收到该请求信息,利用公式(1)计算得到两点之间的距离dAN,并将其返回给水下待定位节点N.水下待定位节点N收到返回的信息后,立刻连续发送3次定位请求信息.船舶在位置B、C、D收到这些定位请求信息,利用公式(1)分别计算出两点之间的距离dBN、dCN、dDN,再将求得的信息返回给水下待定位节点N,具体的通信过程如图 4所示.
|
图 3 多信源动态节点定位图 Fig. 3 Multi-source dynamic node localization |
|
图 4 信息交换图 Fig. 4 Information exchange process |
水下待定位节点N在水流作用下具有移动特性,其在收到船舶的信息后,连续发送3次信息,时间间隔很短,在几秒内就能完成.在计算两点之间距离的时候,依然可以利用TOA测距方法进行计算.水下待定位节点的移动速度较慢,位置变化在非常短的时间内可以忽略不计[22].因此,可以采用方程组(3)解得水下待定位节点N的位置.
当多艘船舶经过水下待定位节点部署区域,利用MDL算法可以得到水下待定位节点的位置.每增加一艘经过水下待定位节点部署区域的船舶,MDL算法运行次数增加一次,这样求得不同的定位结果,将其求平均值,并将所得平均值作为水下待定位节点的最终位置,这样就可提升水下待定位节点的定位精度. MDL算法运行如下.
|
|
在海洋物联网水下待定位节点进行定位的过程中,首先选择数量较为充足的多信源节点进行定位.当信源节点数量少于4个,应将移动船舶与水下待定位节点进行多次通信,以得到足够多的位置信息进行节点的位置计算.当部分节点无法与类似于船舶的信标节点进行通信,而无法得到足够多的定位信息的时候,则可以利用与其周围已经定位的水下节点进行通信,从而让已经定位的水下节点充当信标节点进行辅助定位.最终实现全网范围的水下待定位节点的定位.
大多数商用和民用船舶的位置信息都是公开的,并且可以公开用于水下节点.因此,该算法可以应用于许多领域,如水下环境监测、目标跟踪等.
2 仿真分析在该节中,我们通过仿真分析MSL算法和MDL算法的性能.为了简化,我们将船舶作为信标节点.仿真实验分为两部分:第一部分是MSL算法的仿真实验;第二部分是MDL算法的仿真实验.同时,将MSL和MDL算法的性能与MFLA算法和LSLS算法进行比较. MFLA和LSLS算法考虑受水流影响的节点运动情况,由于这两种算法的水下待定位节点独特的定位过程,致使这两种算法可以用于静态或动态海洋环境;另外,这两种算法的水下待定位节点位置可以通过三边定位方程来计算.因此,本文将所提出的算法分别与MFLA和LSLS算法进行了比较,仿真结果表明了MSL和MDL算法要优于MFLA和LSLS这两种算法.
2.1 参数设置在整个仿真实验中,使用Matlab R2016a作为仿真平台,并对算法参数进行设置.第一部分为MSL算法参数设置,在400 m×400 m×100 m的区域内随机部署了20个水下待定位节点,设置水下待定位节点的通信半径为100 m.第二部分为MDL算法参数设置,水下待定位节点随机部署在相同的区域内, 将船舶移动速度设定为2~20 m/s,水下待定位节点随水流移动的速度设定为0.5 m/s,参与定位的船舶数量设置为1艘,信息发送时隙为1 s,设置水下待定位节点的通信半径为100 m.在整个仿真过程中,将海水温度和盐度设定为15 ℃和3.5%.为了简化,忽略海水温度和盐度的变化.水下待定位节点的Z轴坐标可以通过其压力传感器直接获得.距离估计误差服从标准差为0.3%的正态分布.另外,使用的计算水下待定位节点的定位误差公式[23]为
| $ {d_{{\rm{err}}}} = \sqrt {{{\left( {{x_{{\rm{est}}}} - {x_{{\rm{ori}}}}} \right)}^2} + {{\left( {{y_{{\rm{est}}}} - {y_{{\rm{ori}}}}} \right)}^2} + {{\left( {{z_{{\rm{est}}}} - {z_{{\rm{ori}}}}} \right)}^2}} , $ | (4) |
其中:xest、yest、zest是通过算法计算得到的水下待定位节点的坐标;xori、yori、zori是水下待定位节点的原始坐标.
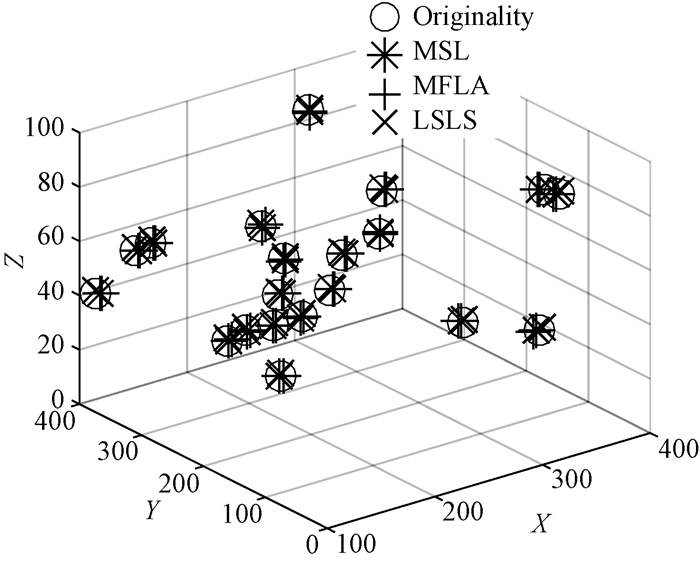
2.2 仿真结果 2.2.1 MSL算法仿真在MSL算法仿真实验中,随机部署的20个水下待定位节点,将其原始位置与计算所得的位置进行比较.比较结果如图 5所示,由图中展示的水下待定位节点的位置可以得到,通过MSL算法计算得到的节点位置更加接近原始节点的位置.
|
图 5 水下节点分布位置 Fig. 5 Nodes′ original and estimated positions |
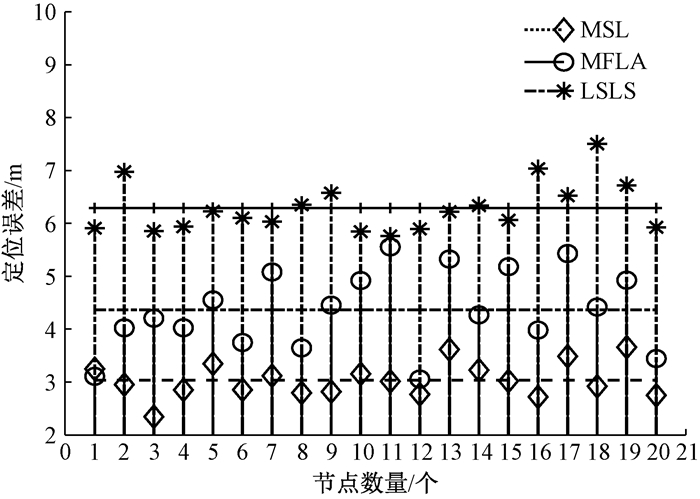
图 6显示了通过MSL、MFLA和LSLS算法分别得到的水下待定位节点的定位误差比较结果.表 1更直观地列出了3种算法定位误差的相关细节.从表 1可以得到,MSL算法的节点定位平均误差减少的倍数分别为MFLA算法的30%和LSLS算法的49%.这是因为MSL算法的节点定位原理与MFLA和LSLS算法不同,MFLA算法用到的节点之间夹角角度变化幅度具有差异性.在LSLS算法中,信标节点与水下待定位节点之间距离的变化,造成了两点之间通信时间的增大,进而使算法中时间运算部分的误差加大.这些因素增加了MFLA和LSLS算法的节点定位误差.
|
图 6 节点定位误差 Fig. 6 Localization errors |
|
|
表 1 定位误差的比较 Tab. 1 Comparison result of localization errors |
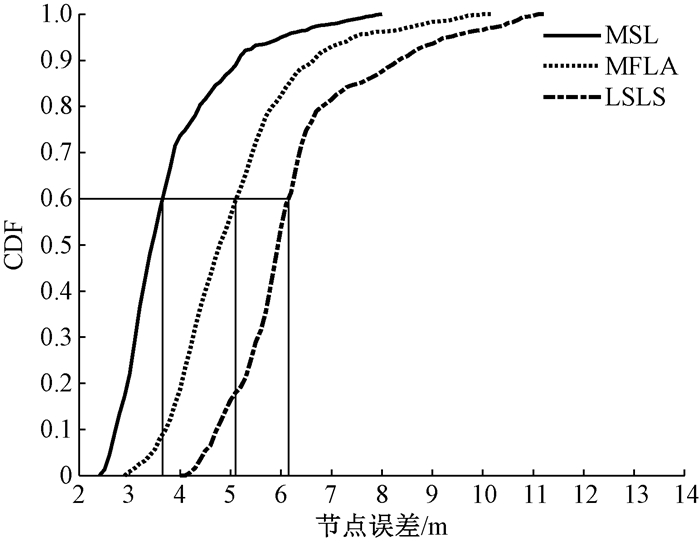
为了分析这3种算法在大规模节点部署中的定位误差,在同一区域内随机部署了1 000个水下待定位节点. 图 7显示了MSL、MFLA和LSLS算法的节点定位误差的CDF.从图中可以看出当CDF值为0.6时,MSL、MFLA和LSLS算法的节点定位误差分别为3.65 m、5.10 m和6.15 m.相比于其他两种算法,MSL算法在静态海洋环境中具有较小的节点定位误差和较好的稳定性.
|
图 7 静态节点定位误差的CDF Fig. 7 CDF of static node localization errors |
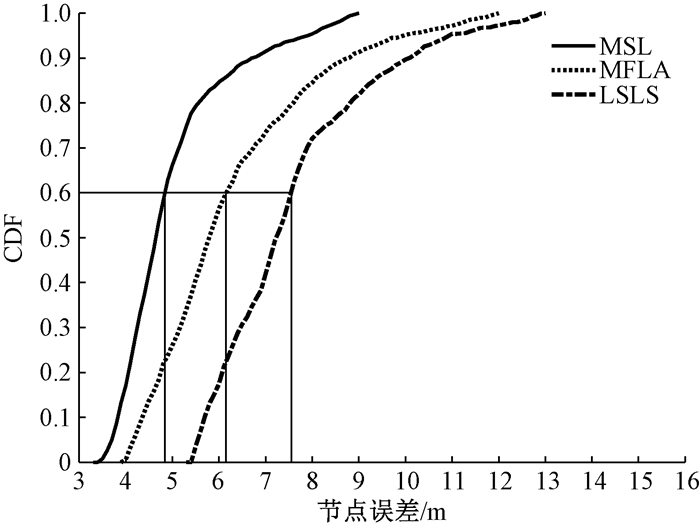
图 8展示了MDL、MFLA和LSLS算法的动态水下待定位节点定位误差CDF.实验结果如图 8所示,当CDF值为0.6时,MDL算法节点定位误差为4.84 m,MFLA和LSLS算法的节点定位误差分别为6.15 m和7.55 m.由此可以得到,在动态的海洋环境中,MDL算法大规模节点定位误差要远小于这两种算法,其稳定性更好.
|
图 8 动态节点定位误差的CDF Fig. 8 CDF of dynamic node localization errors |
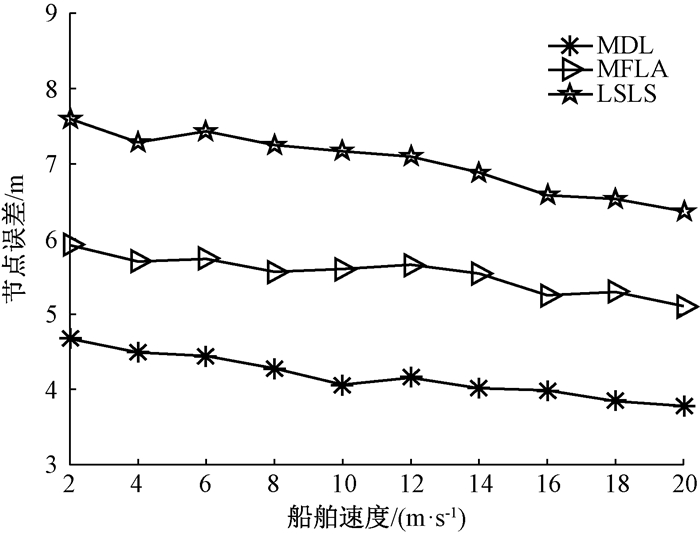
在水下待定位节点动态定位过程中,信标节点的移动速度是一个重要的影响因素.为了研究船舶速度变化的影响,将其速度变化范围设置在2~20 m/s之间.在图 9中,MDL、MFLA和LSLS算法的节点定位误差随着信标节点速度的增加而逐渐减少.对于MDL算法来说,在水下待定位节点定位过程中,船舶和水下待定位节点的移动,以及船舶速度增加,这两个因素致使两点之间通信距离增大,从而提高了三边定位法的求解精度,进而使节点定位误差逐渐减小,图中曲线整体趋势由高到低.MFLA算法采用多跳传输的方法,信标节点和水下待定位节点之间的通信过程相对稳定,由两边(同一侧的两个节点构成一条边)形成的角度变化很小,从而导致节点定位误差变化幅度缓慢. LSLS算法不考虑信标节点的移动性,并且不能很好地通过信标节点来构建锚节点组,因此在节点定位过程中,定位误差变化较大. MDL、MFLA和LSLS算法的平均节点定位误差分别为4.174 5 m、5.108 3 m和7.020 m.与MFLA和LSLS算法相比,MDL算法的平均节点定位误差分别减少了19%和40%.由此可以证明,在动态的海洋环境中,MDL算法的定位精度要高于MFLA和LSLS算法.
|
图 9 MDL、MFLA、LSLS算法船舶速度对定位误差的影响 Fig. 9 Localization errors and speed by MDL, MFLA, LSLS Algorithm |
从上述的仿真实验结果图可以明显看出,MSL和MDL算法的定位误差要小于MFLA和LSLS算法.MSL和MDL算法节点定位过程,需要信标节点的数量仅为一个,且无须其他辅助节点.水下待定位节点与信标节点直接通信,避免了其他节点辅助通信定位带来的误差影响.但是,MFLA算法需要其他辅助节点来构造多跳路径.路径长度(相邻路径的长度由三个相邻节点组成的角度计算)误差随信标节点移动而变大.LSLS算法需要3个节点(包含金、银和铜节点)来形成一个节点组.在本文相同的仿真实验环境中,信标节点的数量只有一个,无法自由形成节点组,这样造成节点组组成部分受到限制,从而导致节点之间通信时延增大.因此,MSL和MDL定位精度更高、稳定性更好、实用性更强.
3 结论根据海洋物联网的特性,提出了多信源海洋物联网定位算法,包括多信源静态定位算法MSL和多信源动态定位算法MDL.该算法可以只利用有定位信息的舰船、航标、建筑物作为信标节点,进行水下节点定位,而不需要其他锚节点等辅助节点.通过仿真实验,证明MSL算法和MDL算法是精确的定位算法,在海洋物联网应用中,具有很好的实用性.
| [1] |
LUO H J, WU K S, HONG F. Ocean barrier: a floating intrusion detection ocean sensor networks[C]//International Conference on Mobile Ad-Hoc and Sensor Networks. Hefei, 2016: 390-394.
(  0) 0) |
| [2] |
夏娜, 王诗良, 郑榕, 等. 基于骨架提取的水下传感器网络刚性定位判别研究[J]. 计算机学报, 2015, 38(3): 589-601. (  0) 0) |
| [3] |
ZHOU Z, CUI J H, ZHOU S L. Efficient localization for large-scale underwater sensor networks[J]. Ad hoc networks, 2010, 8(3): 267-279. DOI:10.1016/j.adhoc.2009.08.005 (  0) 0) |
| [4] |
LUO H J, WU K S, RUBY R, et al. Simulation and experimentation platforms for underwater acoustic sensor networks[J]. ACM computing surveys, 2017, 50(2): 1-44. (  0) 0) |
| [5] |
郭瑛. 活动受限三维水下传感器网络节点定位算法[J]. 软件学报, 2013, 24(1): 33-40. (  0) 0) |
| [6] |
何耀枫, 梁美惠, 陈俐均, 等. 基于物联网的温室环境测控系统[J]. 郑州大学学报(理学版), 2018, 50(1): 90-94. (  0) 0) |
| [7] |
GUO Y, LIU Y T. Localization for anchor-free underwater sensor networks[J]. Computers and electrical engineering, 2013, 39(6): 1812-1821. DOI:10.1016/j.compeleceng.2013.02.001 (  0) 0) |
| [8] |
APARICIO J, JIMENEZ A, ALVAREZ F J, et al. Characterization of an underwater positioning system based on GPS surface nodes and encoded acoustic signals[J]. IEEE transactions on instrumentation and measurement, 2016, 65(8): 1773-1784. DOI:10.1109/TIM.2016.2552699 (  0) 0) |
| [9] |
AHMED M, SALLEH M, CHANNA M I. Routing protocols based on node mobility for underwater wireless sensor network (UWSN): a survey[J]. Journal of network and computer applications, 2017, 78: 242-252. DOI:10.1016/j.jnca.2016.10.022 (  0) 0) |
| [10] |
DAS A P, THAMPI S M. Fault-resilient localization for underwater sensor networks[J]. Ad hoc networks, 2017, 55: 132-142. DOI:10.1016/j.adhoc.2016.09.003 (  0) 0) |
| [11] |
GISINGER C, BALSS U, PAIL R, et al. Precise three-dimensional stereo localization of corner reflectors and persistent scatterers with TerraSAR-X[J]. IEEE transactions on geoscience and remote sensing, 2015, 53(4): 1782-1802. DOI:10.1109/TGRS.2014.2348859 (  0) 0) |
| [12] |
XIAO F, LIU W, LI Z T, et al. Noise-tolerant wireless sensor networks localization via multinorms regularized matrix completion[J]. IEEE transactions on vehicular technology, 2018, 67(3): 2409-2419. DOI:10.1109/TVT.2017.2771805 (  0) 0) |
| [13] |
NICULESCU D, NATH B. Ad hoc positioning system (APS) using AOA[C]//Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies. San Francisco, 2003, 1209196.
(  0) 0) |
| [14] |
BAHL P, PADMANABHAN V N. RADAR: an in-building RF-based user location and tracking system[C]//Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies. Tel Aviv, Israel, 2000: 832252.
(  0) 0) |
| [15] |
BULUSU N, HEIDEMANN J, ESTRIN D. GPS-less low-cost outdoor localization for very small devices[J]. IEEE personal communications, 2000, 7(5): 28-34. DOI:10.1109/98.878533 (  0) 0) |
| [16] |
NICULESCU D, NATH B. Localized positioning in ad hoc networks[J]. Ad hoc networks, 2003, 1(2/3): 247-259. (  0) 0) |
| [17] |
LIU L F, WU J G, ZHU Z W. Multihops fitting approach for node localization in underwater wireless sensor networks[J]. International journal of distributed sensor networks, 2015, 11(7): 682182. DOI:10.1155/2015/682182 (  0) 0) |
| [18] |
CHENG W, THAELER A, CHENG X Z, et al. Time-synchronization free localization in large scale underwater acoustic sensor networks[C]//29th IEEE International Conference on Distributed Computing Systems Workshops. Canada, 2009: 80-87.
(  0) 0) |
| [19] |
HU L X, EVANS D. Localization for mobile sensor networks[C]//Proceedings of the 10th annual international conference on Mobile computing and networking. Philadelphia, 2004: 45-57.
(  0) 0) |
| [20] |
SHEN Z Y, HE Z J, LI S, et al. A multi-quadcopter cooperative cyber-physical system for timely air pollution localization[J]. ACM transactions on embedded computing systems, 2017, 16(3): 70. (  0) 0) |
| [21] |
GUO Y, ZHANG Z. Clock synchronization study for large scale underwater sensor networks[J]. Journal of electronics and information technology, 2014, 36(6): 1498-1503. (  0) 0) |
| [22] |
GUO Y, LIU Y T, LIU G F, et al. Pair-wise collision-based underwater time synchronization[J]. Journal of network and systems management, 2016, 24(4): 813-833. DOI:10.1007/s10922-016-9364-1 (  0) 0) |
| [23] |
张震, 邵星星. 一种SIFT虹膜匹配算法[J]. 郑州大学学报(理学版), 2017, 49(3): 14-19. (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


