边界元法(BEM)是一种有效的工程数值计算方法,具有降维、精度高、灵活和速度快等特点.但因计算过程中形成的线性矩阵方程组的系数矩阵是非对称型满阵,边界元法对大规模的工程问题并不适用.基于BEM的上述问题,很多学者对其进行了深入的研究.文献[1]提出了快速多极展开法(FMM),此算法是一种快速求解积分方程的算法.之后,文献[2]将FMM广义极小残余法(GMRES)结合边界积分方程,得到快速多极边界元(FM-BEM),此方法使计算量和存储量降低到O(N),在很大程度上提高了计算效率,被广泛应用到各个领域.文献[3]将快速多极展开技术用于高阶边界元法,降低了计算量和存储量.文献[4-5]对三维弹塑性摩擦接触多极边界元法进行了研究.并对三维轧制过程,建立了点面摩擦接触模型.近几年来,FM-BEM的应用更加广泛.文献[6]将有限元和FMM-BEM结合,来分析结构声学问题.文献[7]研究了FMM-BEM中基础Laplace方程非负解的存在性.
多极展开法[8]是一种近似方法,展开的阶数越多就越接近真实值.在实际中展开的阶数是有限的,也就是存在项数的截断.误差的估计方法有多种,如文献[9]提出了一种新的估计技巧.而本文依据勒让德函数的相关性质,对三维位势及位势梯度Legendre级数基本解展开的截断误差进行了推导,得出级数展开到p项时的误差估计式,从而得到控制精度的方法.
1 三维位势问题的边界积分方程设有限域为Ω,其表面边界为Γ.已知位势表面为Γ1,已知位势梯度表面为Γ2,且Γ=Γ1+Γ2,则可得Poisson方程的边界积分方程为
| $ {c^i}{u^i}\left( x \right) + \int_\mathit{\Gamma } {{q^ * }\left( {x,y} \right)u\left( y \right){\rm{d}}\mathit{\Gamma }} = \int_\mathit{\Gamma } {{u^ * }\left( {x,y} \right)q\left( y \right){\rm{d}}\mathit{\Gamma }} , $ | (1) |
其中:x为源点;y为边界Γ上的任意一点;ci为边界形状系数;式中所用到的基本解为u*(x, y),
| $ {u^ * }\left( {x,y} \right) = \frac{1}{{4{\rm{ \mathsf{ π} }}\left| {x - y} \right|}} = \frac{1}{{4{\rm{ \mathsf{ π} }}R}};{q^ * }\left( {x,y} \right) = \frac{{\partial {u^ * }\left( {x,y} \right)}}{{\partial n}}, $ | (2) |
其中:q*(x, y)是u*(x, y)在y点处的外法线方向的导数;R为观测点和源点间的距离;n为边界Γ的外法矢.
位势基本解是1/R的函数.为适合多极展开法,将梯度表示为
| $ {q^ * }\left( {x,y} \right) = - \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left[ {{\partial _1}\left( {\frac{1}{R}} \right){n_1} + {\partial _2}\left( {\frac{1}{R}} \right){n_2} + {\partial _3}\left( {\frac{1}{R}} \right){n_3}} \right] = - \frac{1}{{4{\rm{ \mathsf{ π} }}}}{\partial _m}\left( {\frac{1}{R}{n_m}} \right), $ | (3) |
其中:m=1、2、3;
Legendre级数多极展开法是对位势问题基本解中的核函数1/R进行级数展开.其近似程度和展开的项数密切相关,展开的项数越多,就越接近真实值.但展开的项数过多,只是增加计算的时间,对提高精度影响不大,所以展开项数一般截断到某一项p,下面对多极展开中的截断误差进行分析.
2.1 位势基本解截断误差设O为坐标原点, X(r, θ, φ)为场点, Xi(ρi, αi, βi)为源点,两点的相对距离为r/ρi,两点距离为
| $ R = \left\| {X - {X_i}} \right\| = \sqrt {\rho _i^2 + {r^2} - 2{\rho _i}r\cos \gamma } , $ |
则根据Legendre多项式的母函数得到
| $ \cos\gamma = \cos\theta \cos{\alpha _i} + \sin \theta \sin {\alpha _i}\cos \left( {\varphi - {\beta _i}} \right). $ |
定理1 在极坐标中场点和源点的距离为R,则基本解基于Legendre级数展开的截断误差为
证明 由公式(2),可得
| $ \begin{array}{l} {E_p} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\frac{1}{R} - {{\left( {\frac{1}{R}} \right)}_p}} \right| = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\sum\limits_{n = 0}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \gamma } \right)} - \sum\limits_{n = 0}^p {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \gamma } \right)} } \right| = \\ \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \gamma } \right)} } \right| \le \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}} } \right|\left| {{P_n}\left( {\cos \gamma } \right)} \right|, \end{array} $ |
根据Legendre函数的正交性[10]可得
| $ \begin{array}{l} {E_p} \le \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}} } \right|\sqrt {\frac{1}{{2\left( {n + 1} \right) + 1}}} \le \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}} } \right|\frac{1}{{\sqrt {2p + 3} }} \le \\ \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{1}{r}\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^n}}}\frac{1}{{\sqrt {2p + 3} }}} \le \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{1}{{r - \rho }}{\left( {\frac{\rho }{r}} \right)^{p + 1}}\frac{1}{{\sqrt {2p + 3} }}. \end{array} $ |
结合远近场划分准则[11], r大于点集半径a的2倍,ρ小于点集的半径a.min(r-ρ)>a,max(
定理2 若球坐标系下源点为Xi(ρi, αi, βi),场点为X(r, θ, φ),且满足cos ν=cos θcos α+sin θ·sin αcos(φ-β),那么
| $ \left| {\frac{{\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha }}{{\sqrt {1 - {{\cos }^2}\nu } }}} \right| \le 1. $ | (4) |
证明 要证式(4),即证[cos θsin αcos(φ-β)-sin θcos α]2≤1-cos2 ν.由夹角间的关系得:
| $ \begin{array}{l} {\cos ^2}\nu = {\left[ {\cos \theta \cos \alpha + \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right)} \right]^2} = {\cos ^2}\theta {\cos ^2}\alpha + {\sin ^2}\theta {\sin ^2}\alpha {\cos ^2}\left( {\varphi - \beta } \right) + \\ 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right), \end{array} $ |
| $ \begin{array}{l} {\left[ {\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha } \right]^2} = {\cos ^2}\theta {\sin ^2}\alpha {\cos ^2}\left( {\varphi - \beta } \right) + {\sin ^2}\theta {\cos ^2}\alpha - \\ 2\sin \theta \cos \alpha \cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right). \end{array} $ |
则有[cos θsin αcos(φ-β)-sin θcos α]2+cos2 ν=cos2 α+sin2 α cos2(φ-β)≤1.
定理3 若球坐标系下源点为Xi(ρi, αi, βi),场点为X(r, θ, φ),且满足cosν=cosθcosα+sinθ·sinαcos(φ-β),那么
| $ \left| {\frac{{\sin \alpha \sin \left( {\varphi - \beta } \right)}}{{\sqrt {1 - {{\cos }^2}\nu } }}} \right| \le 1. $ | (5) |
证明 要证式(5),即证1-cos2 ν-sin2 αsin2(φ-β)≥0.
由夹角间的关系得
| $ \begin{array}{l} 1 - {\cos ^2}\nu - {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) =\\ 1 - {\cos ^2}\theta {\cos ^2}\alpha - {\sin ^2}\theta {\sin ^2}\alpha {\cos ^2}\left( {\varphi - \beta } \right) - {\sin ^2}\theta {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) - \\ {\cos ^2}\theta {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) -\\ 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right) = 1 - {\cos ^2}\theta {\cos ^2}\alpha - {\sin ^2}\theta {\sin ^2}\alpha - \\ {\cos ^2}\theta {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) - 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right) = \left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right) - \\ {\cos ^2}\theta {\cos ^2}\alpha - {\sin ^2}\theta {\sin ^2}\alpha - {\cos ^2}\theta {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) - 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right) = \\ {\cos ^2}\theta {\sin ^2}\alpha + {\sin ^2}\theta {\cos ^2}\alpha - {\cos ^2}\theta {\sin ^2}\alpha {\sin ^2}\left( {\varphi - \beta } \right) - 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right) = \\ {\cos ^2}\theta {\sin ^2}\alpha {\cos ^2}\left( {\varphi - \beta } \right) + {\sin ^2}\theta {\cos ^2}\alpha - 2\cos \theta \cos \alpha \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right) = \\ {\left( {\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha } \right)^2} \ge 0. \end{array} $ |
定理4 球坐标系下,位势梯度的各个分量的截断误差分别为ΔEpr、ΔEpθ、ΔEpφ,则
| $ \left\| {\Delta {E_p}} \right\| = \sqrt {{{\left( {\Delta {E_{pr}}} \right)}^2} + {{\left( {\Delta {E_{p\theta }}} \right)}^2} + {{\left( {\Delta {E_{p\theta }}} \right)}^2}} \le \frac{1}{{4{\rm{ \mathsf{ π} }}{a^2}}}\sqrt {\frac{{\left( {3p + 4} \right)\left( {p + 2} \right)}}{{2p + 3}}} {\left( {\frac{1}{2}} \right)^{p + 1}}. $ |
证明 设位势梯度的截断误差为ΔEp,则
| $ \Delta {E_p} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial n}}\left| {\frac{1}{R} - {{\left( {\frac{1}{R}} \right)}_p}} \right| = \frac{{\partial {E_p}}}{{\partial n}} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial n}}\left[ {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \nu } \right)} } \right], $ |
令
由Legendre函数的微商表示与连带的Legendre函数的微商间的关系可得[10]:
| $ {\nu _\theta } = \frac{{{\rho ^n}}}{{{r^{n + 2}}}}\left[ {\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha } \right]P_n^1\left( {\cos \nu } \right){\left( {1 - {{\cos }^2}\nu } \right)^{ - 1/2}}, $ |
| $ {\nu _\varphi } = \frac{{{\rho ^n}}}{{{r^{n + 1}}}}\left[ {\frac{{ - \sin \theta \sin \alpha \sin \left( {\varphi - \beta } \right)}}{{\sin \theta }}} \right]P_n^1\left( {\cos \nu } \right){\left( {1 - {{\cos }^2}\nu } \right)^{ - 1/2}}. $ |
根据Legendre函数的正交性及远近场划分准则可得[11]
| $ \begin{array}{l} \left| {\Delta {E_{pr}}} \right| = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial r}}\left| {\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \nu } \right)} } \right| = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{r - \rho }}{{\left( {\frac{\rho }{r}} \right)}^{p + 1}}} \right)\left| {{P_n}\left( {\cos \nu } \right)} \right| = \\ \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left| {\left[ { - \frac{1}{{{{\left( {r - \rho } \right)}^2}}}{{\left( {\frac{\rho }{r}} \right)}^{p + 1}} - \frac{1}{{r - \rho }}\left( {p + 1} \right)\frac{{{\rho ^{p + 1}}}}{{{r^{p + 2}}}}} \right]} \right|\left| {{P_n}\left( {\cos \nu } \right)} \right| \le \\ \frac{1}{{4{\rm{ \mathsf{ π} }}}}\left[ {\frac{1}{{{a^2}}}{{\left( {\frac{\rho }{r}} \right)}^{p + 1}} + \frac{{p + 1}}{{{a^2}}}{{\left( {\frac{\rho }{r}} \right)}^{p + 1}}} \right]\frac{1}{{\sqrt {2p + 3} }} \le \frac{1}{{4{\rm{ \mathsf{ π} }}{a^2}}}\frac{{p + 2}}{{\sqrt {2p + 3} }}{\left( {\frac{1}{2}} \right)^{p + 1}}. \end{array} $ |
结合定理2,可得
| $ \begin{array}{l} \left| {\Delta {E_{p\theta }}} \right| = \left| {\frac{1}{{4{\rm{ \mathsf{ π} }}r}}\left[ {\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha } \right]{{\left( {1 - {{\cos }^2}\nu } \right)}^{ - 1/2}}\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}P_n^1\left( {\cos \nu } \right)} } \right| = \\ \frac{1}{{4{\rm{ \mathsf{ π} }}r}}\left| {\left[ {\cos \theta \sin \alpha \cos \left( {\varphi - \beta } \right) - \sin \theta \cos \alpha } \right]{{\left( {1 - {{\cos }^2}\nu } \right)}^{ - 1/2}}} \right|\frac{1}{{r - \rho }}{\left( {\frac{\rho }{r}} \right)^{p + 1}}P_n^1\left( {\cos \nu } \right) \le \\ \frac{1}{{4{\rm{ \mathsf{ π} }}a}}\frac{1}{a}{\left( {\frac{\rho }{r}} \right)^{p + 1}}\sqrt {\frac{{\left( {p + 2} \right)!}}{{\left( {2p + 3} \right)p!}}} \le \frac{1}{{4{\rm{ \mathsf{ π} }}{a^2}}}\sqrt {\frac{{\left( {p + 1} \right)\left( {p + 2} \right)}}{{2p + 3}}} {\left( {\frac{1}{2}} \right)^{p + 1}}. \end{array} $ |
结合定理3,可得
| $ \begin{array}{l} \left| {\Delta {E_{p\varphi }}} \right| = \left| {\frac{1}{{4{\rm{ \mathsf{ π} }}r}}\sin \alpha \sin \left( {\varphi - \beta } \right){{\left( {1 - {{\cos }^2}\nu } \right)}^{ - 1/2}}\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}P_n^1\left( {\cos \nu } \right)} } \right| = \\ \frac{1}{{4{\rm{ \mathsf{ π} }}r}}\left| {\sin \alpha \sin \left( {\varphi - \beta } \right){{\left( {1 - {{\cos }^2}\nu } \right)}^{ - 1/2}}} \right|\sum\limits_{n = p + 1}^\infty {\frac{{{\rho ^n}}}{{{r^{n + 1}}}}P_n^1\left( {\cos \nu } \right)} \le \\ \frac{1}{{4{\rm{ \mathsf{ π} }}a}}\frac{1}{a}{\left( {\frac{\rho }{r}} \right)^{p + 1}}\sqrt {\frac{{\left( {p + 1} \right)\left( {p + 2} \right)}}{{2p + 3}}} \le \frac{1}{{4{\rm{ \mathsf{ π} }}{a^2}}}\sqrt {\frac{{\left( {p + 1} \right)\left( {p + 2} \right)}}{{2p + 3}}} {\left( {\frac{1}{2}} \right)^{p + 1}}. \end{array} $ |
综上可得
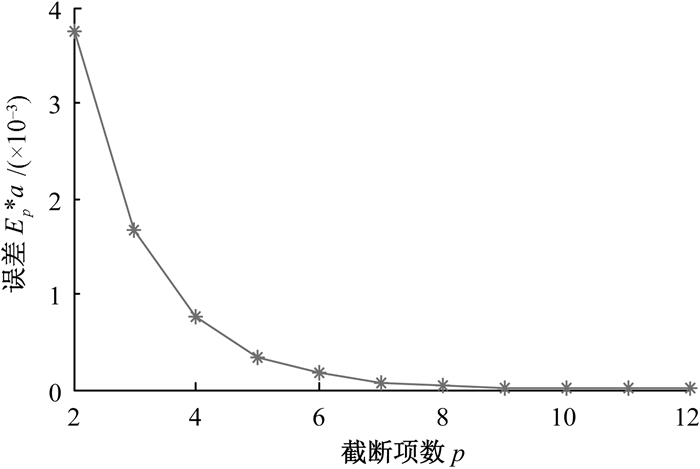
由定理1可得三维位势基本解的截断误差式,截断项数p取不同的值时,将Ep*a看作一个整体,其截断误差结果如图 1所示.由定理4可得位势梯度的截断误差.截断项数p取不同的值时,将‖ΔEp‖*a2看作一个整体,其截断误差结果如图 2所示.
|
图 1 位势的误差(r/ρ=2) Figure 1 Error for potential |
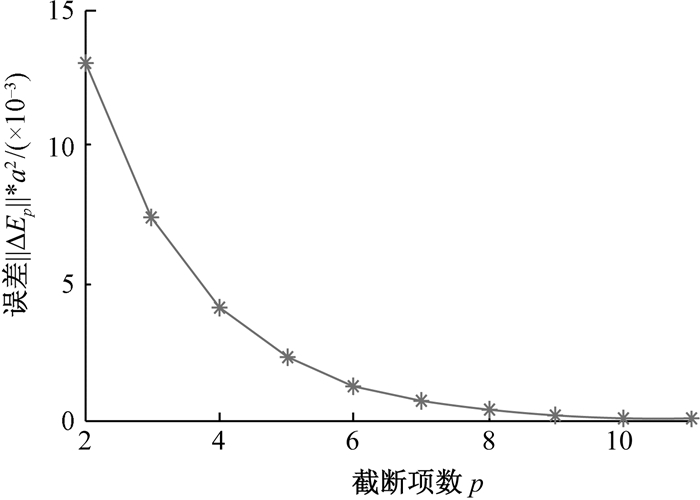
从图 1和图 2中可以看出,当相对距离r/ρ一定时,随着截断项数p的增加,位势和位势梯度的截断误差都在逐渐缩小.
|
图 2 位势梯度的误差(r/ρ=2) Figure 2 Error for potential gradient |
因此,截断项数p对多极展开的计算量、存储量以及求解精度具有重要的影响,适当地选取p值在实际工程计算中尤为重要.由文献[12]知,为了获得一个较高的精度,截断项数p应与log1/2(ε)同阶.对于给定的精度要求,就可以用式p=[-log2ε]+1([]代表取整), 给出其所要求的截断项数.
3 结论本文从三维位势问题位势基本解入手,对其Legendre级数展开进行详细分析,给出位势及位势梯度Legendre级数基本解的截断误差估计式,并给出一定精度时,截断项数p的选取表达式.研究结果进一步完善了Legendre级数FM-BEM的理论体系,为快速FM-BEM解决位势问题提供了强有力的理论依据.
| [1] |
GREENGARD L, ROKHLIN V. A fast algorithm for particle simulations[J]. Journal of computational physics, 1987, 73(2): 325-348. DOI:10.1016/0021-9991(87)90140-9 (  0) 0) |
| [2] |
ROKHLIN V. Rapid solution of integral equations of classical potential theory[J]. Journal of computational physics, 1985, 60(2): 187-207. DOI:10.1016/0021-9991(85)90002-6 (  0) 0) |
| [3] |
宁德志, 滕斌, 勾莹. 快速多极子展开技术在高阶边界元方法中的实现[J]. 计算力学学报, 2005, 22(6): 700-704. (  0) 0) |
| [4] |
刘德义. 三维弹塑性摩擦接触多极边界元法和四辊轧机轧制模拟[D]. 秦皇岛: 燕山大学, 2003.
(  0) 0) |
| [5] |
YU C, LIU D, ZHENG Y, et al. 3-D rolling processing analysis by fast multipole boundary element method[J]. Engineering analysis with boundary elements, 2016, 70: 72-79. DOI:10.1016/j.enganabound.2016.04.012 (  0) 0) |
| [6] |
WU F, LIU G R, LI G Y, et al. A coupled ES-BEM and FM-BEM for structural acoustic problems[J]. Noise control engineering journal, 2014, 62(4): 196-209. DOI:10.3397/1/376220 (  0) 0) |
| [7] |
李瑞. 一类非局部(p, q)-Laplace方程非负解的存在性[J]. 郑州大学学报(理学版), 2016, 48(2): 5-10. (  0) 0) |
| [8] |
ROKHLIN L G V. A new version of the fast multipole method for the Laplace equation in three dimensions[J]. Acta numerica, 1996, 6: 229-269. (  0) 0) |
| [9] |
孙淑珍, 石翔宇. 抛物型积分微分方程双线性元方法的新估计[J]. 郑州大学学报(理学版), 2016, 48(4): 6-9. (  0) 0) |
| [10] |
刘式适, 刘式达. 特殊函数[M]. 北京: 气象出版社, 2002, 326-361.
(  0) 0) |
| [11] |
SHEN G X, YU C X, LIU D Y.Fast multipole boundary element method in rolling engineering and its research progress[C]//Conference Computational Methods in Engineering. Nanjing, 2009:18-20.
(  0) 0) |
| [12] |
GREENGARD L F. The rapid evaluation of potential fields in particle systems[M]. Cambridge MA: Mit Press, 2003, 121-141.
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49


