2. 中国科学院大学 计算与控制学院 北京 100049
2. School of Computer Science and Technology, University of Chinese Academy of Sciences, Beijing 100049, China
科学计算和工程问题中经常涉及稠密对称矩阵的特征求解问题,通常的处理方法是先通过正交变换把原矩阵化为三对角矩阵,如Householder或Givens方法,再求解三对角阵的特征值和特征向量。三对角阵的特征求解算法有很多种,常用的有QR法、二分法、分而治之方法和多近似健壮表示(multiple relatively robust representations, MRRR)方法等等,本文工作基于分治法展开。
对称三对角阵特征求解的分治算法,最早由文献[1]提出, 文献[2]作出了改进,提高了该算法的求解精度和特征向量的正交性。分治算法采用分而治之思想,将原矩阵划分为若干小的子矩阵,先求出子矩阵的特征分解,接着通过修正计算,逐级合并子矩阵的结果,回代得到原矩阵的特征分解。分治法具有很强的灵活性,对于大规模三对角矩阵特征问题的并行求解是一种比较理想的算法。
现有很多模型都实现了针对分治算法的并行化,如基于分布式存储的消息传递接口(message passing interface, MPI)进程级并行[3],基于共享内存的openMP线程级并行,还有基于对称多处理结构(symmetrical multi procession, SMP)的MPI/openMP混合并行模型[4]等。以openMP为代表的线程级并行模型主要基于数据并行的考量,通过把数据划分到多个核上实现并行,该模型在计算负载均衡的条件下能取得较好的效果。但对于分治和递归类的场景,当数据依赖呈复杂网状结构时,则不能很好地实现负载均衡。
Cilk是一个基于任务的并行编程模型,为串行程序的并行化提供了向量化、视图等机制(http://supertech.csail.mit.edu/cilk/manual-5.4.6.pdf),通过关键字来声明操作,改造后的代码具有语义化、可读性强的特点。Cilk为共享内存系统提供了一个高效的任务窃取调度器,适合用来实现高效的多核任务并行。
1 三对角矩阵特征求解分治算法的基本原理 1.1 三对角矩阵的划分对任意n阶实对称三对角矩阵T,基于秩1修正作如下划分。
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}}&{{\beta _1}}&{}&{}&{}\\ {{\beta _1}}&{{\alpha _2}}&{{\beta _2}}&{}&{}\\ {}&{{\beta _2}}&{{\alpha _3}}& \ddots &{}\\ {}&{}& \ddots & \ddots &{{\beta _n}}\\ {}&{}&{}&{{\beta _n}}&{{\alpha _n}} \end{array}} \right] \Rightarrow \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_1}}&0\\ 0&{{\mathit{\boldsymbol{T}}_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \beta &\beta \\ \beta &\beta \end{array}} \right], $ |
其中:T1、T2是三对角子矩阵块,β元素所在矩阵构成原矩阵的修正矩阵。为使修正矩阵元素一致,T1的末位元素和T2的首元素都减去相同的β。经过划分原矩阵变为
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{T'}} + \beta z{z^{\rm{T}}}, $ |
其中Z=(0, …, 0, 1, 1, 0, …, 0)T。1的索引代表对原矩阵进行划分的位置。对于划分后的矩阵T′,若规模未达到指定阈值,则继续划分。
1.2 分治法求解过程若划分后的子矩阵规模达到设定阈值,调用QR或者其他算法, 得到子矩阵T1、T2的特征值分解为
| $ {\mathit{\boldsymbol{T}}_1} = {\mathit{\boldsymbol{Q}}_1}{\mathit{\boldsymbol{D}}_1}\mathit{\boldsymbol{Q}}_1^{\rm{T}};{\mathit{\boldsymbol{T}}_2} = {\mathit{\boldsymbol{Q}}_2}{\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{Q}}_2^{\rm{T}}, $ | (1) |
此时T可以表示为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_1}}&{}\\ {}&{{\mathit{\boldsymbol{Q}}_2}} \end{array}} \right]\left( {\mathit{\boldsymbol{D}} + \beta \mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{T}}}} \right)\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Q}}_1^{\rm{T}}}&{\mathit{\boldsymbol{Q}}_2^{\rm{T}}} \end{array}} \right], $ | (2) |
其中:$\mathit{\boldsymbol{D}} = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_1}}&{}\\ {}&{{\mathit{\boldsymbol{D}}_2}} \end{array}} \right]; {\mathit{\boldsymbol{x}}^{\rm{T}}} = \left({\mathit{\boldsymbol{q}}_1^{\rm{T}}, \mathit{\boldsymbol{q}}_2^{\rm{T}}} \right), {\mathit{\boldsymbol{q}}_1}, {\mathit{\boldsymbol{q}}_2}$分别是Q1的最后一行和Q2的第一行元素构成的向量。
要求T的特征分解T=QΛQT,先求D+βxxT的特征分解,使得D+βxxT=PΛPT,再令${\boldsymbol{Q}}=\left[\begin{array}{cc} {{\boldsymbol{Q}}_{1}} & {} \\ {} & {{\boldsymbol{Q}}_{2}} \end{array}\right]$,即可求得T的特征分解。
对于D+βxxT的特征分解,需要根据划分后矩阵的特征值和原矩阵特征值的间隔性[5],通过求解对应的secular方程
| $ 1 + \beta \sum\limits_i {\frac{{x_i^2}}{{{d_i} - \lambda }}} = 0, {d_i} = {D_{ii}}, $ | (3) |
得到相应的特征值λ。文献[5]讨论了方程(3)根的分布特性和解法,在特征区间内使用牛顿法或拉格朗日法迭代逼近区间内的特征值,线性时间内即可收敛。解出所有的特征值后,再通过式(D-λI)-1x[1]求得每个特征值对应的特征向量,回代到式(1)中得到T的特征分解。
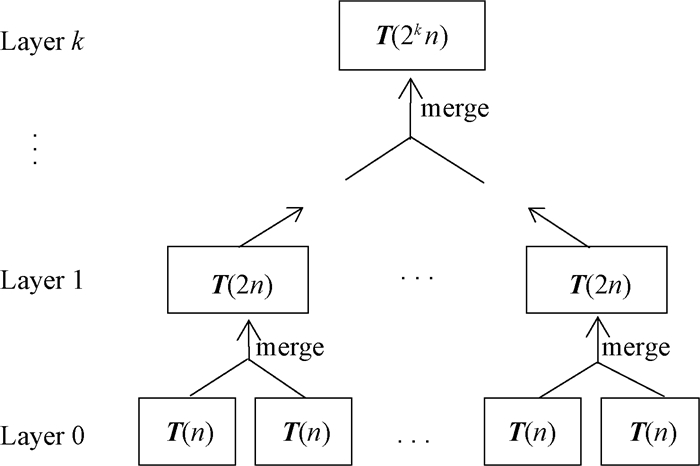
整个求解过程可看作逻辑上的树型结构,如图 1所示。在叶子结点进行特征求解,在非叶子结点上进行特征合并。
|
图 1 分治算法结构 Fig. 1 The structure of divide and conquer method |
降阶:合并过程中如果D的主对角线上出现了相同的元素或者X向量中出现0元素时,文献[6]中提出要先进行deflation操作,通过Givens正交旋转变换进行迭代逼近前的预处理,部分特征值和特征向量就能原地得到,从而避免了特征区间内迭代不收敛的情况。
正交性:如果特征值前后间隔过小,使用原公式求解得到的特征向量会逐渐丢失正交性。文献[2]给出了特征向量的改进求法,引入了新的计算方式来修正计算过程中结果的正交性。
2 基于Cilk的节点内并行 2.1 节点内并行算法对于单节点内的三对角矩阵块,使用分治法求解主要包含两个过程:调用特征求解算法求出最小划分矩阵的特征分解,逐步合并特征值和特征向量。由于每个子矩阵的特征计算以及同级子矩阵之间的合并过程是相互独立的,下面结合Cilk任务并行机制,给出分治算法在节点内多核环境下的并行化递归实现。
|
|
先判断输入矩阵的规模,如果矩阵规模小于等于指定阈值,调用QR或其他算法进行特征求解,返回结果;否则执行Cilk任务划分,划分矩阵T得子矩阵T1、T2,并行对T1、T2递归调用算法1,求出子矩阵的特征分解后,进行排序和迭代逼近等操作,合并子矩阵的特征值和特征向量,得到T的特征分解,返回结果。
Cilk在程序递归执行过程中不断划分新的任务,产生Cilk线程去处理,并把其分配到空闲的核上,和父线程并行执行。Cilk通过任务窃取(Work-Stealing)的方式来执行调度:当一个核完成自己的任务而其他核还有很多任务未完成,此时会将忙的核上的任务重新分配给空闲的核。
算法1计算过程中涉及矩阵乘法、排序、迭代逼近等操作,可以利用Cilk提供的数据并行机制加速,Cilk通过数据划分形成一个个可供调度的线程级任务并行执行。空闲线程通过工作密取从其他线程获取一部分工作量,Cilk利用贪心策略来进行任务调度分配,能够避免单核上出现任务过载和饥饿等待的问题,同时能将密取的次数控制在最低水平,减少密取带来的性能开销。
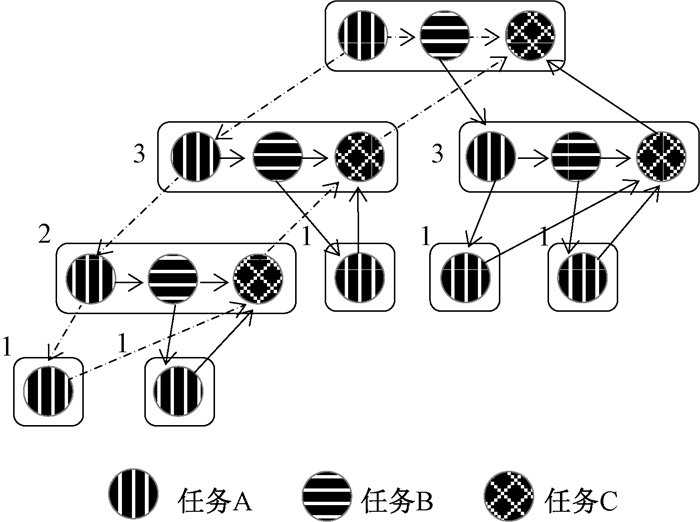
2.2 算法分析一个Cilk线程可看作在同步、生成新线程或返回结果之前所能执行的最长序列化指令集(http://www.cilkplus.org/cilk-documentation-full)。根据此定义,求解过程中,递归调用T1之前的过程可以看作一个Cilk线程,记为任务A,递归调用T2的过程可以看作任务B,同步及合并过程可以看作任务C。现假设程序只进行了4次嵌套调用,则全局任务划分后生成的任务流程如图 2所示。
|
图 2 节点内任务并行流程 Fig. 2 Task flow of divide and conquer method inside nodes |
程序从有向无环图的最上面开始执行,对应递归的最外层。每一个出度大于1的结点都会派生出新的Cilk线程,执行新的任务。设程序执行过程产生的所有的Cilk线程数为W(图 2中节点数),关键路径长度为S(图 2中虚线部分路径长度)。则程序的并行性Parallelism可表示为
| $ \mathit{Parallelism}{\rm{ = }}\mathit{W}{\rm{/}}\mathit{S}\mathit{。} $ | (4) |
程序的执行时间Time满足
| $ \mathit{Time > max}\left( {T(W/P} \right), \left. {T\left( S \right)} \right), $ | (5) |
其中:P是处理器核数;T(W/P)表示所有任务平均到每个核上运行的时间;T(S)表示关键路径上的任务运行花费的总时间。
3 基于MPI/Cilk的多节点混合并行 3.1 混合并行算法实现分治算法的MPI多节点并行,需要把原始矩阵按图 1结构划分成小的子矩阵分发到叶子结点上进行初步计算,然后通过MPI通信,每棵子树的父结点收集子结点的计算结果后进行汇总,把整理后的结果重新发送到子结点进行合并操作,重复此过程,直到返回到图 1中的根结点。为了减少进程间通信,充分利用Cilk任务并行机制,需要对原矩阵进行较粗粒度的划分,以榨取单节点处理器的计算性能。并且在消息传递时,只使用一个线程作为主控线程,以减少通信开销。
对于n阶对称三对角矩阵T在N个进程上的特征求解,假设N=2q,n=2p,算法初始时把原矩阵划分为N个子矩阵,每个子矩阵阶数为2p-q,设为2k,下面给出分治算法的在多进程间的混合并行实现。
算法2 分治算法基于MPI/Cilk的节点间并行。
第一步,对于划分到N个进程上的每个初始子矩阵,调用算法1求出各部分特征值和特征向量。
第二步,进行p次循环(p对应图 1中树的深度),每次循环先把进程分组并确定主控进程来进行结果收发。对每个MPI进程,需要根据自己的进程类别,按序选择执行下列步骤:
1) 组内进程向主控进程发送本进程求得的所有局部特征值,如果本进程是上一轮循环的主控进程,则还要向本轮主控进程发送上一轮计算得到的特征向量矩阵。
2) 主控进程收集属于同一组进程中所有求得的局部特征值和特征向量,对特征值进行排序,并保留排序后的位置索引数组。按照1.2节的过程拼接Z1、Z2成一个新向量X,根据位置索引将X排序, 将排好序的特征值均匀地划发到组内各进程,同时也把向量X传到组内各进程。
3) 组内进程接收主控进程发送过来的排好序的部分特征值和向量X,求解secular方程和特征向量,并发送结果给主控进程。
4) 主控进程更新当前循环的特征向量矩阵,接着执行下一轮循环。
3.2 算法分析在对特征值进行排序后,同时记录排序后各位置元素的原来位置的索引,避免对特征向量重复排序,方便下一轮特征向量的计算。算法2中步骤3)和4)中涉及大量计算密集型操作,占据程序执行的主要时间,同样可以通过Cilk数据并行机制划分多个线程级子任务并行执行。
在第p轮循环中,从0号进程开始, 每2p+1个进程分为一组,每隔2p+1个进程被选为主控线程,每个小组内共进行3(2p+1-1)次通信,每轮循环的通信次数是3N(2p+1-1)/2p+1。
分治算法总的时间复杂度介于O(n2)~O(n3)之间,空间复杂度为O(n2),误差和矩阵规模的关系为$O(\sqrt{n} \varepsilon)$。
若单节点内划分的数据粒度适当粗时,就能利用Cilk机制充分发挥多核处理器的计算和调度能力,得到较好的计算性能,同时减少进程间通信次数,降低通信开销。
4 实验结果与分析我们在中科院“元”级超算上针对该混合模型进行了数值实验,实验运行在CPU Ⅱ计算队列上,节点上搭载的是Intel E5-2680 V3芯片,每块芯片包含12个主频为2.5 GHz的计算核心。MPI程序使用Intel mpiicpc编译器编译,编译时链接Cilk Plus运行,计算过程中使用了部分MKL库中的函数。实验对象是30 000阶实对称三对角矩阵,矩阵划分求解的规模阈值设为200阶,最终求出全部特征值和特征向量。实验通过环境变量设置使用4和8个线程进行实验,为方便对比,已测出实验在单节点单线程环境下平均串行时间为882.53 s。
表 1是纯MPI方法和MPI/Cilk方法在4~64个核参与计算下所用时间比较。从表 1可以看出,对于同一矩阵,使用相同数目的核参与计算时,MPI/Cilk混合方法所用时间要少于纯MPI方法,性能要优于纯MPI方法,而8线程的MPI/Cilk方法性能要优于4线程的,这表明8线程的混合模型有更好的负载均衡。在较少节点参与计算时,获得加速效果较为明显,这说明对数据进行粗粒度划分时能取得较好性能。
|
|
表 1 MPI模型和MPI/Cilk模型程序的时间 Tab. 1 Time of pure MPI method and MPI/Cilk method |
表 2是MPI模型和MPI/Cilk模型程序的加速比对比。表 2数据表明,MPI/Cilk方法具有比纯MPI方法更高的加速比,而8线程MPI/Cilk方法的加速比开始时和4线程接近,随着可供调度的核数增多,加速效果逐渐超过了4线程方法。MPI/Cilk方法的加速比在一开始上升较快,随着进程数的增加,加速效果随之下降,但仍比纯MPI方法变缓更慢,拥有更好的扩展性。对于给定规模的矩阵,当参与计算的核数超过一定数量时,计算效果的提升越来越有限,出现这种现象主要是因为计算任务粒度变细和进程间通信开销增加导致的。
|
|
表 2 MPI模型和MPI/Cilk模型程序的加速比 Tab. 2 Speedup of pure MPI method and MPI/Cilk |
表 3和表 4分别给出了Cilk和openMP这两种模型的计算时间和加速比的比较,其中openMP模型采用数据并行方式,通过指导语句对涉及计算的部分进行了并行化。从结果可以看出,在参与计算的核数较少时,openMP模型的效果要优于Cilk模型,原因是计算粒度较大时,数据并行占主导地位。而随着参与计算的核数增多,Cilk模型的效果逐渐超过openMP模型,此时可供调度的核数增多,Cilk动态调度的优势逐渐体现。
|
|
表 3 MPI/openMP模型和MPI/Cilk模型程序的时间 Tab. 3 Time of MPI/openMP method and MPI/Cilk method |
|
|
表 4 MPI/openMP模型和MPI/Cilk模型程序的加速比 Tab. 4 Speedup of MPI/openMP method and MPI/Cilk method |
本文针对实对称三对角矩阵特征求解的分治算法,提出了一种基于MPI/Cilk的混合并行实现算法。在节点间,通过粗粒度计算任务的划分,在相同的求解效率下减少了所需要的计算进程和进程间的通信次数。在节点内,利用Cilk的任务并行机制提高CPU的利用率,改善了负载均衡,提高了并行度。实验结果体现了该算法的性能。该算法还可进一步研究,如运用数据并行机制加速特征合并过程,研究Cilk线程启动数和数据划分粒度对性能的影响以及同openMP的任务并行机制对比等。
| [1] |
CUPPEN J J M. A divide and conquer method for the symmetric tridiagonal eigenproblem[J]. Numerische mathematik, 1980, 36(2): 177-195. DOI:10.1007/BF01396757 (  0) 0) |
| [2] |
GU M, EISENSTAT S C. A stable and efficient algorithm for the rank-one modification of the symmetric eigenproblem[J]. SIAM journal on matrix analysis and applications, 1994, 15(4): 1266-1276. DOI:10.1137/S089547989223924X (  0) 0) |
| [3] |
TISSEUR F, DONGARRA J. A parallel divide and conquer algorithm for the symmetric eigenvalue problem on distributed memory architectures[J]. SIAM journal on scientific computing, 1999, 20(6): 2223-2236. DOI:10.1137/S1064827598336951 (  0) 0) |
| [4] |
ZHAO Y H, CHEN J, CHI X B. Solving the symmetric tridiagonal eigenproblem using MPI/OpenMP hybrid parallelization[M]. Heidelberg: Springer, 2005: 164-173.
(  0) 0) |
| [5] |
AMMAR G S, REICHEL L, SORENSEN D C. An implementation of a divide and conquer algorithm for the unitary eigen problem[J]. ACM transactions on mathematical software, 1992, 18(3): 292-307. DOI:10.1145/131766.131770 (  0) 0) |
| [6] |
MELMAN A. Numerical solution of a secular equation[J]. Numerische mathematik, 1995, 69(4): 483-493. DOI:10.1007/s002110050104 (  0) 0) |
| [7] |
王进, 晏世凯, 高延雨, 等. 基于MPI的ML-kNN算法并行[J]. 郑州大学学报(理学版), 2018, 50(3): 34-38. WANG J, YAN S K, GAO Y Y, et al. Parallelization of ML-kNN based on MPI[J]. Journal of Zhengzhou university(natural science edition), 2018, 50(3): 34-38. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


