2. 解放军信息工程大学 数学工程与先进计算国家重点实验室 河南 郑州 450000
2. State Key Laboratory of Mathematical Engineering and Advanced Computing, PLA Information Engineering University, Zhengzhou 450000, China
隐写技术和加密技术是提供秘密信息交流的两种方法。然而传统的加密技术目的是加密信息,而不是隐藏秘密通信的行为存在,容易引起第三方的注意。隐写技术主要是将信息隐藏在载体中,通信行为从视觉上是安全的,不容易引起注意。为了在网络上安全传播有价值的信息,信息隐藏技术越来越引起专家和学者的注意。Turner[1]提出最低有效位的方法来隐藏信息,虽然方法有效但是隐藏量不大,而且随着检测技术的发展很容易检测出信息的存在。为了嵌入更多的信息,并可以逆向提取,Tian[2]提出了差值扩展(difference expansion, DE)的方法来隐藏信息,并提取信息,具有里程碑式的意义。目前实现可逆信息隐藏的方法大致分4类:基于无损压缩[3]、基于差值扩展[2, 4]、基于误差扩展[5-11]和基于直方图平移[12-15]。Thodi等[5]提出的预测误差扩展方法(prediction error expansion, PEE)被一致认为是一种高效的方法。Li等[6]提出了基于像素排序的预测方法(pixel value ordering, PVO),由于该方法具有保真度比较高,不用定位像素值的优点,成为研究热点。K元像素排序的预测方法(PVO-K)[7]充分利用了可嵌入的最值像素,较传统方法的嵌入量提高了很多。Qu等[8]进一步改进了算法,取得了创新性的突破,不再以分块为嵌入单位,提出基于像素的像素排序方法(pixel-based pixel value ordering, PPVO)。随着社会的发展,学术文献和办公文件的数字化,安全隐蔽的扫描文档图像传输也亟待研究,文献[16-17]采用半色调技术和四叉树技术处理扫描文档图像。张敏情等[18]提出基于Paillier同态公钥加密系统的算法,孔咏骏等[19]提出基于序列动态选择的PVO算法。秘密信息越来越多样化,虽然所有的秘密信息都可以转化为二进制串,但是很少有考虑扫描文档的冗余。将扫描文档图像的冗余背景消除掉,只保留实际内容的信息,并将其转化为二进制串,会大大减少实际嵌入量,从而也实现了大容量的有效嵌入,保留较好的图像品质。本文考虑数据流和扫描文档两种秘密信息形式,消除无意义的冗余背景,提出基于信息预处理的PPVO可逆信息隐藏算法。将扫描的文档作为秘密信息,主要采用半色调技术和四叉树技术对扫描文档进行处理,处理的数据流为真正嵌入的数据,使嵌入容量有很大的提高。同时本文着眼于提高嵌入容量和提高图像的保真度,改进PPVO算法,主要思路是将秘密信息分成数据流和扫描文档图像两种形式,对数据流进行映射变化,提高嵌入信息量;对扫描文档图像进行半色调和四叉树处理,嵌入真正的信息,从而实现大容量信息的传递。
1 相关工作 1.1 传统PVO算法像素值排序(PVO)算法是通过光栅扫描将图像分成若干相互不重叠的子块,假设子块B(w·h)有w·h个像素,记作(X1, X2, …, X(w·h)),将像素值进行排序,得到升序的像素值序列(Xπ(1), Xπ(2), …, Xπ(w·h))。每个像素误差通过公式计算得到,
| $ P E_{\max }=X_{\pi(w \cdot h)}-X_{\pi(w \cdot h-1)}, P E_{\max }=X_{\pi(1)}-X_{\pi(2)}。$ |
修改误差值将秘密信息b∈{0, 1}嵌入误差值中,
| $ \widetilde{P E}_{\max }=\left\{\begin{array}{ll} P E_{\max }, & P E_{\max }=0, \\ P E_{\max }+b, & P E_{\max }=1, \widetilde{P E}_{\min } \\ P E_{\max }+1, & P E_{\max }>1, \end{array}=\left\{\begin{array}{ll} P E_{\min }, & P E_{\min }=0, \\ P E_{\min }-b, & P E_{\min }=-1, \\ P E_{\min }-1, & P E_{\min }<-1_{\circ} \end{array}\right.\right. $ |
然后修改最大和最小像素值,实现数据的嵌入,
| $ \tilde{X}_{\pi(w \cdot h)}=X_{\pi(w \cdot h-1)}+\widetilde{P E}_{\max }, \tilde{X}_{\pi(1)}=X_{\pi(2)}+\widetilde{P E}_{\min }。$ |
通过上述操作很容易看出数据嵌入到了最大像素值和最小像素值中,并且像素的排列顺序没有发生改变,有利于可逆运算,保证了数据的顺利提取。
1.2 PVO-K算法在PVO-K算法中,考虑到像素序列中最大值和最小值可能不止一个,将所有最大值像素(最小值像素)作为数据嵌入对象。在传统的PVO算法中,当最大像素值或最小像素值分别有两个或更多时,误差值是0,此像素值是不能嵌入对象的。在PVO-K算法中,含有k个最大或最小像素值,嵌入量更大,并且效果也更好。每个像素块的像素排序为(Xπ(1), Xπ(2), …, Xπ(w·h)),最后k+1像素关系表示为Xπ(w·h-k) < Xπ(w·h-k+1)=…=Xπ(w·h),k个最大像素值为p,像素误差值PE=Xπ(w·h-k+1)-p。最后,所有k个最大像素值修改为
传统的PVO算法通过修改每个分块中的最大和最小像素值将秘密信息嵌入原始图像中,虽然预测准确率高,但是嵌入容量不够大,最多每个分块中嵌入2比特的数据。针对这一问题,Qu等[8]利用目标像素的上下文概念,提出了以目标像素为嵌入目标的新方法(PPVO)。针对每一个目标像素X,像素X的上下文像素有CN个,记作:C=(C1, C2, …,CCN)。图 1以CN=15为例,展示了目标像素以及上下文像素。通过像素的上下文来预测误差,
| $ P E=\left\{\begin{array}{ll} X-\max (C), & X \geqslant \max (C), \\ X-\min (C), & X \leqslant \min (C)。\end{array}\right. $ |

|
图 1 目标像素及上下文临近像素 Fig. 1 The context pixels of pixel X |
根据max(C)和min(C)是否相等两种情况来修改像素值,当max(C)≠min(C)时,
| $ \widetilde{P E}=\left\{\begin{array}{ll} P E+b, & X=\max (C), \\ P E+1, & X>\max (C), \\ P E-b, & X=\min (C), \\ P E-1, & X<\min (C), \end{array}\right. $ | (1) |
| $ \tilde{X}=\left\{\begin{array}{ll} \max (C)+\widetilde{P E}, & X \geqslant \max (C), \\ \min (C)+\widetilde{P E}, & X \leqslant \min (C)。\end{array}\right. $ | (2) |
当max(C)=min(C)时,还要解决溢出问题。在计算预测误差之前,将所有灰度值为255或0的像素修改为254和1,并在定位图中用1表示,即LM(i)=1。像素值初始值是254或1的像素不变,令LM(i)=0。像素误差值通过公式(3)得到,像素修改值通过公式(4)得到,
| $ \widetilde{P E}=\left\{\begin{array}{ll} P E+b, & \max (C)=254, X=\max (C), \\ P E-b, & \max (C) \neq 254, X=\min (C), \\ P E-1, & \max (C) \neq 254, X<\min (C), \end{array}\right. $ | (3) |
| $ \tilde{X}=\left\{\begin{array}{ll} \max (C)+\widetilde{P E}, & \max (C)=254, X=\max (C), \\ \min (C)+\widetilde{P E}, & \max (C) \neq 254, X \leqslant \min (C)。\end{array}\right. $ | (4) |
本文挖掘在像素排序预测误差系列方法中嵌入容量的能力,提出了新的PPVO算法,将数据流秘密信息进行压缩映射变换,具有很好的通用性,而且当载体图像是纹理复杂的图像时嵌入信息意义更大;将扫描文档图像进行半色调和四叉树处理,处理后的数据采用PPVO算法嵌入原始载体图像中。
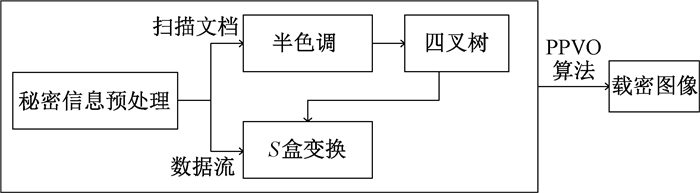
2.1 算法思想本文算法的核心是充分利用图像的冗余空间,并且对数据流秘密信息进行无损压缩映射变换,对扫描文档图像进行半色调和四叉树处理[17],大大增加了嵌入容量。为了实现这一目标,进行了以下工作:1) 将秘密信息进行了映射变换,每6比特信息映射为4比特,压缩变换后的数据流采用PPVO算法嵌入原始载体;2) 除了对秘密信息进行数据流分析,还考虑了扫描文档图像;3) 将扫描文档图像进行半色调和四叉树处理,处理的数据作为秘密信息,采用PPVO算法嵌入原始载体。具体的算法流程图如图 2所示。
|
图 2 算法流程图 Fig. 2 Framework of the proposed scheme |
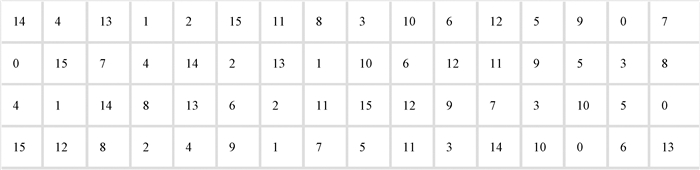
使用DES加密算法中S盒压缩秘密信息的容量,使得实际嵌入量提高1.5倍。S盒是DES算法的核心,是唯一的非线性部分,每个S盒可以实现6比特的输入,得到4比特的输出。根据这一特性,可以被应用到压缩和扩展变换中,行号被专门存储,并通过专门的安全通道传输。为了保持传统PVO算法的高准确率特性,本文沿用了PPVO算法的思想,同时为了进一步扩大嵌入容量,将秘密信息进行了映射变换。每6比特信息为一组b1b2b3b4b5b6,首先取中间4比特组成二进制数b2b3b4b5,两端2比特组成二进制数b1b6。令b2b3b4b5=r, b1b6=h,在S盒的h行r列找到对应数字D,D在0~15之间,用二进制表示D=c1c2c3c4,就是S盒的输出。DES加密算法涉及8个S盒,S1盒是其中一个(图 3)。
|
图 3 S1盒 Fig. 3 S1 box |
本文采用半色调方法处理灰度文档图像,得到二值图像。这就意味着每8比特的像素值只需要1比特显示,所以使得文件缩小为原来的1/8。二值图像中,白色背景的地方显示为1,其他含有内容的地方显示为0。相对来说含有信息的内容比背景更重要,采用四叉树的方法将内容从背景中分离出来。主要的处理过程如下:
1) 将任意尺寸的扫描图像处理成N·N的尺寸,然后进行半色调技术的误差扩散方法处理;
2) 每个图像的像素值对应一个矩阵。当矩形的尺寸大于4×4时,将矩形分割成4个子矩形,重复进行分割,直到不满足分割条件;
3) 分割后产生的矩形块很多,意味着块坐标比较多,所以对矩形子块再通过水平和垂直方向进行合并,将合并之后含有内容的子块坐标记录下来,并将内容从图像中提取出来,使用文本文档存储;
4) 采用十进制编码算法处理3)的文件,忽略左侧是0的比特串,并以文本文档存储;
5) 将4)的文档内容转换成二进制串,作为PPVO算法的嵌入内容。
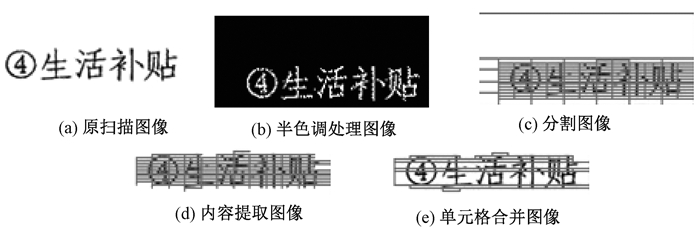
如图 4所示,以2.27 KB(2 332字节)的扫描文档图像(a)为例,经过步骤3)处理之后文件大小为19.4 KB(19 900字节),经过步骤4)处理之后的文件大小为3.60 KB(3 696字节),最后转换成二进制串是460字节。在本文当中嵌入的秘密信息是460字节的二进制串,达到的效果是实现2 332字节的扫描文档图像的嵌入。
|
图 4 扫描图像及处理图像 Fig. 4 Scanned document image and processed image |
本文为了确保算法的可逆性,使用目标像素上下文计算预测值。例如,如图 1所示,目标像素X的预测值
| $ \hat{X}=\left\{\begin{array}{ll} \min \left(C_{1}, C_{2}\right), & C_{3} \geqslant \max \left(C_{1}, C_{2}\right), \\ \max \left(C_{1}, C_{2}\right), & C_{3} \leqslant \min \left(C_{1}, C_{2}\right), \\ C_{1}+C_{2}-C_{3}, & \ \ \ \ \ \ \ \ \ \text { 其他 } 。\end{array}\right. $ |
本文结合PPVO算法和信息映射变换来提高嵌入容量,主要的嵌入过程为:
1) 当嵌入数据信息是数据流时,数据信息进行映射变换;
2) 当嵌入数据信息是扫描文档图像时,进行半色调和四叉树处理。
用公式(1)~(4)对载体图像进行信息嵌入。
2.3 提取和恢复过程秘密信息的提取和载体图像的恢复是嵌入过程的逆过程,
1) 对载密图像进行逆向扫描,实现秘密信息的提取,分两种情况。
a) max(C)≠min(C)。
b) max(C)=min(C)。VC=254:①
2) 当秘密信息是数据流时,根据获得秘密信息查找对应的映射表,从而得到原始的秘密信息。
举例说明逆映射过程。假设提取出来的秘密信息是00110110001101100011011000110110,首先对信息进行分组,每组4比特,分成8组0011、0110、0011、0110、0011、0110、0011、0110;然后根据记录的映射表号对每组进行映射得到8组数据,每组6比特,111000、101010、111000、101010、111000、101010、111000、101010。逆映射变换之后的数据就是原始的秘密信息。
3) 当秘密信息是扫描文档图像时,获得的数据流是扫描文档的尺寸信息、含有内容的单元格的4个坐标值、内容信息等。根据坐标值和内容信息,我们可以恢复扫描文档图像。
3 实验结果与分析原始载体图像会随着嵌入信息量的增大,图像越来越失真。如何评价载密图像的质量,最直接的方式就是比较载密图像与原始载体图像之间的差剖面,也就是可视误差来评判图像的品质。均方误差(mean squared error,MSE)和峰值信噪比(peak signal to noise ratio,PSNR)是常用的评价标准。
均方误差的公式为
| $ M S E=\frac{1}{M \times N} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{N}\left(f^{\prime}(i, j)-f(i, j)\right)^{2}, $ |
其中:f(i, j) 表示原始载体图像的像素值;f′(i, j)表示载密图像的像素值;M和N表示图像的长度与宽度。
峰值信噪比用于衡量图像有效信息与噪声之间的比率,能够反映图像是否失真,计算公式为
| $ P S N R=10 \log \frac{z^{2}}{M S E}, $ |
其中:z表示图像的最大像素值,一般取值255。PSNR值越大,表示图像失真越少。在原始载体图像嵌入数据之后,像素值发生了改变,在相同嵌入量的情况下,像素值改变越小图像的质量越好。
为了验证算法的性能,采用Windows 2010操作系统下的Matlab 7.0作为实验平台,选用512×512的灰度图像Lena、Baboon和Airplane为原始载体图像,秘密信息是随机产生的二进制串时,分别与传统的PVO算法[6]、PVO-K算法[7]、PPVO算法[8]和改进的PPVO算法(IPPVO)[9]进行比较;当处理的秘密信息是扫描文档图像时,与文献[16-17]比较。图 5是采用本文算法达到最大嵌入容量时,原始载体图和载密图的效果图。

|
图 5 原图和载密图 Fig. 5 Cover image and embedded image |
本文主要侧重考虑图像的嵌入容量,通过表 1可以看出PPVO算法与PVO算法和PVO-K算法相比,嵌入容量有了大幅度的提高,而本文比PPVO类算法嵌入容量又有了更大的提高。Lena和Airplane图像因为平滑区域多,嵌入容量提升幅度比较大,而纹理复杂的Baboon图像在前三种方法上提升幅度不大,而本文方法对纹理复杂的图像嵌入信息时效果更明显。通过表 2和表 3可以看出,随着嵌入容量的增大,本文算法不仅能保持较好的PSNR值,而且可以嵌入更多的信息。对于载体图像是Baboon来说,本文算法最大嵌入量是22 500比特,其他算法嵌入量不超过15 000比特。当嵌入量是20 000比特时,本文算法仍然能够保持较好的图像品质。
|
|
表 1 最大嵌入容量对比 Tab. 1 Maximum embedding capacity comparison |
|
|
表 2 嵌入10 000比特时PSNR对比 Tab. 2 PSNR comparison when embedding 10 000 bits |
|
|
表 3 嵌入20 000比特时PSNR对比 Tab. 3 PSNR comparison when embedding 20 000 bits |
PVO算法的特点是高预测准确率,而且保真度较高,因此成为近些年的研究热点之一。本文在PPVO算法的基础上,引入了数据流信息映射转换及半色调和四叉树处理扫描文档,大大提高了信息的嵌入量,并且保真度也很好。实验数据表明,本文的算法保证了图像的保真度,同时也提高了嵌入量。算法中S盒的行号另行存储,不与秘密信息放在一起,并通过专门的案例通道传输。下一步的研究工作可以着眼于新的映射变换研究,降低行号记录的空间占有率。
| [1] |
TURNER L F. Digital data security system: EP19890904115[P]. 1991-09-01.
(  0) 0) |
| [2] |
TIAN J. Reversible data embedding using a difference expansion[J]. IEEE transactions on circuits and systems for video technology, 2003, 13(8): 890-896. DOI:10.1109/TCSVT.2003.815962 (  0) 0) |
| [3] |
CELIK M U, SHARMA G, TEKALP A M, et al. Lossless generalized-LSB data embedding[J]. IEEE transactions on image processing, 2005, 14(2): 253-266. DOI:10.1109/TIP.2004.840686 (  0) 0) |
| [4] |
ALATTAR A M. Reversible watermark using the difference expansion of a generalized integer transform[J]. IEEE transactions on image processing, 2004, 13(8): 1147-1156. DOI:10.1109/TIP.2004.828418 (  0) 0) |
| [5] |
THODI D M, RODRIGUEZ J J. Expansion embedding techniques for reversible watermarking[J]. IEEE transactions on image processing, 2007, 16(3): 721-730. DOI:10.1109/TIP.2006.891046 (  0) 0) |
| [6] |
LI X L, LI J, LI B, et al. High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion[J]. Signal processing, 2013, 93(1): 198-205. DOI:10.1016/j.sigpro.2012.07.025 (  0) 0) |
| [7] |
OU B, LI X L, ZHAO Y, et al. Reversible data hiding using invariant pixel-value-ordering and prediction-error expansion[J]. Signal processing: image communication, 2014, 29(7): 760-772. DOI:10.1016/j.image.2014.05.003 (  0) 0) |
| [8] |
QU X C, KIM H J. Pixel-based pixel value ordering predictor for high-fidelity reversible data hiding[J]. Signal processing, 2015, 111: 249-260. DOI:10.1016/j.sigpro.2015.01.002 (  0) 0) |
| [9] |
何文广, 熊刚强, 周珂, 等. 基于改进像素排序预测的大容量可逆数据隐藏[J]. 计算机应用研究, 2018, 35(1): 266-271. HE W G, XIONG G Q, ZHOU K, et al. Larger capacity reversible data hiding using improved pixel-based pixel value ordering prediction[J]. Application research of computers, 2018, 35(1): 266-271. DOI:10.3969/j.issn.1001-3695.2018.01.057 (  0) 0) |
| [10] |
MEIKAP S, JANA B. Directional PVO for reversible data hiding scheme with image interpolation[J]. Multimedia tools and applications, 2018, 77(23): 31281-31311. DOI:10.1007/s11042-018-6203-2 (  0) 0) |
| [11] |
WENG S W, PAN J S, LI L D. Reversible data hiding based on an adaptive pixel-embedding strategy and two-layer embedding[J]. Information sciences, 2016, 369: 144-159. DOI:10.1016/j.ins.2016.05.030 (  0) 0) |
| [12] |
NI Z C, SHI Y Q, ANSARI N, et al. Reversible data hiding[J]. IEEE trans on circuits and system for video technology, 2016, 16(3): 354-362. (  0) 0) |
| [13] |
TSAI P, HU Y C, YEH H L. Reversible image hiding scheme using predictive coding and histogram shifting[J]. Signal processing, 2009, 89(6): 1129-1143. DOI:10.1016/j.sigpro.2008.12.017 (  0) 0) |
| [14] |
FU D S, JING Z J, ZHAO S G, et al. Reversible data hiding based on prediction-error histogram shifting and EMD mechanism[J]. AEU-international journal of electronics and communications, 2014, 68(10): 933-943. DOI:10.1016/j.aeue.2014.04.015 (  0) 0) |
| [15] |
PAN Z B, HU S, MA X X, et al. Reversible data hiding based on local histogram shifting with multilayer embedding[J]. Journal of visual communication and image representation, 2015, 31: 64-74. DOI:10.1016/j.jvcir.2015.05.005 (  0) 0) |
| [16] |
SOLEYMANI S H, TAHERINIA A H. High capacity image steganography on sparse message of scanned document image (SMSDI)[J]. Multimedia tools and applications, 2017, 76(20): 20847-20867. DOI:10.1007/s11042-016-4009-7 (  0) 0) |
| [17] |
SOLEYMANI S H, TAHERINIA A H. High capacity image data hiding of scanned text documents using improved quadtree[EB/OL]. (2018-03-22)[2020-12-10]. arXiv: 1803.11286.
(  0) 0) |
| [18] |
张敏情, 李天雪, 狄富强, 等. 基于Paillier同态公钥加密系统的可逆信息隐藏算法[J]. 郑州大学学报(理学版), 2018, 50(1): 8-14. ZHANG M Q, LI T X, DI F Q, et al. Reversible data hiding algorithm based on paillier homomorphic public key encryption system[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(1): 8-14. (  0) 0) |
| [19] |
孔咏骏, 张敏情, 彭菓玉, 等. 基于序列动态选择的PVO可逆信息隐藏算法[J]. 郑州大学学报(理学版), 2019, 51(3): 34-41. KONG Y J, ZHANG M Q, PENG G Y, et al. A PVO reversible data hiding algorithm based on sequence dynamic selection[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(3): 34-41. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


