2. 网络与信息安全武警部队重点实验室 陕西 西安 710086
2. Key Laboratory of Network and Information Security of the Chinese People′s Armed Police, Xi′an 710086, China
互联网技术的进一步发展引起信息过载问题:信息量的大幅增长使用户难以从过量信息中获取所需信息。因此过滤用户不需要的信息成为亟须解决的开放性问题。解决信息超载的一种重要途径是使用搜索引擎,但是存在如必须主动搜索、没有个性化推荐等问题。推荐算法是目前被广泛应用的一种信息过滤的手段,根据用户或者项目(如音乐、商品、视频等)的特征建立模型用以预测用户对其尚未考虑项目的偏好。推荐算法的出现,从大量可用项目中预测了用户需求,使用户有更合适的选择,产生了巨大的经济效益。好的推荐算法能够吸引用户长期使用。因此,推荐算法从用户角度考虑,可以为用户提供个性化的服务,而从服务提供商角度考虑,则能提高用户忠诚度,防止用户流失。
好的推荐系统需要提供个性化和准确的推荐,因此需要尽可能多地掌握用户的个性化信息。用户提供越多的信息,则获得的推荐越准确,但是泄露的隐私信息也就越多,从而导致推荐系统与用户隐私保护之间的矛盾[1]。常见推荐系统的隐私保护方法包括:k-anonymous方法[2]、分布式推荐系统[3]和代理组件[4]等设计架构、同态加密[5]等手段。随着同态加密效率的提高,涌现出许多基于同态加密的研究成果[6-7],使用同态加密来保护推荐系统中的用户隐私将成为一种越来越有前景的方法。
本文提出了一种基于TW16协议的同态隐私保护推荐算法,TW16是文献[8]提出的一种基于好友关系的推荐协议,该协议可以基于用户好友以及陌生人的评分来对用户未评分的项目进行预测,并使用同态加密技术保护用户的隐私。本文在该方案基础上,通过增加活跃用户的评分权值、对参数设置进行优化和增加计算缓存的方法,构造并实现了一种准确高效的基于同态加密的隐私保护推荐协议。
1 推荐算法本节对基于好友关系的推荐算法和类同态加密方案(somewhat homomorphic encryption,SHE)进行介绍。
X代表数据集,x←X表示从X中随机均匀地选取一个x,|X|表示X的大小。如果χ是一个分布,那么s←χ表示s是从χ分布中抽样得到的。给定两个向量X和Y,使用X·Y表示两个向量的内积,使用‖X‖表示X的欧氏距离。
在推荐算法中,推荐条目集合表示为I=(1, 2, …, b, …, M),用户x的评分表示为向量Rx=(rx, 1, …, rx, b, …, rx, M),其评分r∈{0, 1, 2, 3, 4, 5}。如果某个条目i尚未被评分,则其评分值rx, i=0,评分结果为一个矩阵。推荐算法用来预测用户尚未评分的rx, i。
给定两个用户x和y,其对应的评分向量Rx和Ry,余弦相似度定义为
| ${sim}(x, y)=\left(\boldsymbol{R}_{x} \cdot \boldsymbol{R}_{y}\right) /\left\|\boldsymbol{R}_{x}\right\| \cdot\left\|\boldsymbol{R}_{y}\right\|。$ |
对于∀b∈[1,M],若rx, b∈Rx≠0,则令已评分向量Qx=(qx, 1, …, qx, b, …,qx, M)中的qx, b=1,即Qx用以标记用户对某项目是否进行标记。用rx代表用户x的平均评分,即$\left\lceil\sum\limits_{i \in B} r_{x, i} / \sum\limits_{i \in B} q_{x, i}\right\rfloor$。
本文使用平均绝对误差(mean absolute error,MAE)来衡量推荐算法的推荐是否准确,
| $MAE = \left( {\sum\limits_{{{\hat r}_{u, i}} \in \mathit{\Gamma }} {\left| {{{\hat r}_{u, i}} - {r_{u, i}}} \right|} } \right)/|\mathit{\Gamma }|, $ |
其中:Γ表示推荐算法预测的评分集;${\hat r_{u, i}}$表示预测的评分;ru, i表示真实的评分。MAE越低,则代表推荐算法越准确。
2 基于同态加密的隐私保护推荐算法在本节中,首先对TW16中描述的推荐算法进行介绍,然后说明对该系统进行的改进和优化。
给定一个用户u和一个陌生人集合Tu,输入陌生人集合Tu对项目b的评价,预测算法定义为
| $p_{u, b}^* = {\bar r_u} + 0.5 \cdot \sum\limits_{t \in {T_u}} {{q_{t, b}}} \cdot \left( {{r_{t, b}} - {{\bar r}_t}} \right)/\sum\limits_{t \in {T_u}} {{q_{t, b}}} , $ | (1) |
其中:pu, b*为输出预测的u对项目b的评价结果;0.5表示陌生人的权重值。将评分进行标准化来代替直接使用某用户的评分避免了出现不同用户对评分严苛程度不同而影响预测的准确性。其余符号在前面已给出说明。使用陌生人参与运算可以解决推荐算法中的冷启动问题,而且能减少用户好友的隐私信息泄露。
给定一个用户u和一个好友集合Fu,输入好友集合Fu对项目b的评价,预测算法定义为
| $p_{u, b}^{**} = {\bar r_u} + \left( {\sum\limits_{f \in {F_u}} {{q_{f, b}}} \cdot \left( {{r_{f, b}} - {{\bar r}_f}} \right) \cdot {w_{u, f}} \cdot \sum\limits_{i = 1}^M {{q_{f, f}}} /\mathit{\boldsymbol{M}}} \right)/\left( {\sum\limits_{f \in {F_u}} {{q_{f, b}}} \cdot {w_{u, f}}} \right), $ | (2) |
其中:pu, b**为输出预测的u对项目b的评价结果;wu, f为好友f对u评分的影响权重。相比于原方案,本方案加入了评价次数权重,即好友f的评价次数与所有参与计算的用户的平均评价次数之比,权重代表该好友参与评价的频繁程度,乐于评价的好友其评价也更具参考价值。
将计算完毕的pu, b*和pu, b**代入等式pu, b=ρ·pu, b*+(1-ρ)·pu, b**,0≤ρ≤1,即可计算用户u对项目b评分的最终预测。本文使用同态加密来对用户隐私进行保护,由于同态加密通常更适用于处理整数,所以使用整数α、β构造小数权重β/(α+β),预测算法为
| $p_{u, b}=\beta /(\alpha+\beta) \cdot p_{u, b}^{*}+\alpha /(\alpha+\beta) \cdot p_{u, b}。$ | (3) |
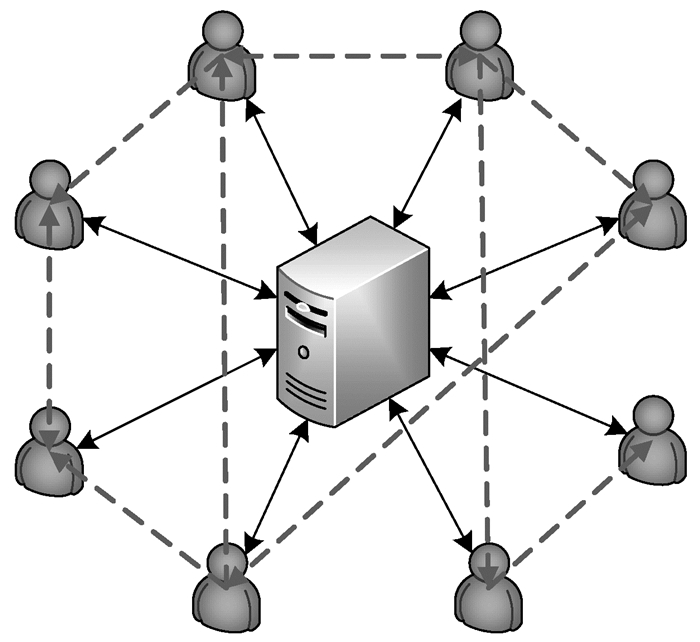
推荐算法中有大量的用户参与提供数据,用户之间并不直接联系,故需要一个中心化的服务提供商来沟通参与协议的所有用户,并向请求推荐结果的用户提供服务。系统中存在中心化的服务提供商和大量的用户,用户好友之间可以单向关注也可双向关注,简化的系统架构图如图 1。
|
图 1 中心化的推荐算法结构图 Fig. 1 Structure of centralized recommendation algorithm |
当用户想要预测某未评分项目b的预测评分时,进行如下协议。
参考上文中的预测算法,协议共分为3个阶段。第1阶段,服务提供商根据公式(1)获取陌生人的加密输入;第2阶段,服务提供商根据公式(2)获取好友的加密输入;第3阶段,用户u根据公式(3)可得知预测结果,而服务提供商没有获取用户隐私信息。
用户u生成二进制向量Ib,第b个元素为1,使用SHE加密算法采用逐比特加密的方式将Ib加密为[Ib]u=Enc(PKu, Ib)=([Ib]u(1), …, [Ib]u(M))并将结果发送到服务器。服务器再将PKu发送至随机选择且愿意参与计算的陌生人集Tu,将[Ib]u转发给Tu中的每个陌生人。每个陌生人t使用PKu和(Rt, Qt),作如下同态运算,
| $\left[2 \cdot q_{t, b}\right]_{u}=\sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(\cdot, {Enc}\left(P K_{u}, 2 \cdot q_{t, i}\right), \left[\boldsymbol{I}_{b}^{(i)}\right]_{u}\right),\\ \left[\boldsymbol{R}_{t} \cdot \boldsymbol{I}_{b}\right]_{u}=\sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(\cdot, {Enc}\left(P K_{u}, r_{t, i}\right), \left[\boldsymbol{I}_{b}^{(i)}\right]_{u}\right)\left[q_{t, b} \cdot\left(\boldsymbol{R}_{t} \cdot \boldsymbol{I}_{b}-\bar{r}_{t}\right)\right]_{u}=\\ {Eval}\left(\cdot, \left[\boldsymbol{q}_{t, b}\right]_{u}, {Eval}\left(+, \left[\boldsymbol{R}_{t} \cdot \boldsymbol{I}_{b}\right]_{u}, {Enc}\left(P K_{u}, -\bar{r}_{t}\right)\right)\right)。$ |
用户u将加密后的权重[wu, f]u=Enc(PKu, wu, f)发送到服务提供商,服务提供商向用户的好友f∈Fu发送[wu, f]u和[Ib]u,f使用PKu,[Ib]u,[wu, f]u和(Rf, Qf)计算
| $\left[q_{f, b}\right]_{u}=\sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(\cdot, {Enc}\left(P K_{u}, q_{f, i}\right), \left[\boldsymbol{I}_{b}^{(i)}\right]_{u}\right), \\ \left[q_{f, b} \cdot\left(\boldsymbol{R}_{f} \cdot \boldsymbol{I}_{b}-\bar{r}_{f}\right) \cdot w_{u, f} \cdot \sum\limits_{i=1}^{M} q_{f, i}\right]_{u}={Eval}\left(\cdot, {Eval}\left(\cdot, \left[q_{f, b}\right]_{u}, \left[w_{u, f}\right]_{u}\right)\right., \\ \left.{Eval}\left(\cdot, {Eval}\left(+, \left[\boldsymbol{R}_{f} \cdot \boldsymbol{I}_{b}\right]_{u}, {Enc}\left(P K_{u^{\prime}}-\bar{r}_{f}\right)\right), \sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(+, q_{f, i}\right)\right)\right), $ |
完成后将结果发送给服务提供商。
服务提供商首先计算[nT]u、[dT]u、[nF]u、[dF]u,然后计算[X]u和[Y]u。
| $\left[n_{T}\right]_{u}=\sum\limits_{t \in T_{u}}\left[q_{t, b} \cdot\left(\boldsymbol{R}_{t} \cdot \boldsymbol{I}_{b}-\bar{r}_{t}\right)\right]_{u}, \left[d_{T}\right]_{u}=\sum\limits_{t \in T_{u}}\left[2 \cdot q_{t, b}\right]_{u}, \left[n_{F}\right]_{u}=\sum\limits_{f \in F_{u}}\left[q_{f, b} \cdot\left(\boldsymbol{R}_{f} \cdot \boldsymbol{I}_{b}-\bar{r}_{f}\right) \cdot w_{u, f}\right]_{u}, \\ \left[d_{F}\right]_{u}=\sum\limits_{f \in F} {Eval}\left(\cdot, \left[q_{f, b}\right]_{u}, \left[w_{u, f}\right]_{u}, \boldsymbol{M}\right), [\boldsymbol{X}]_{u}=\left[\beta \cdot n_{T} \cdot d_{F}+\alpha \cdot n_{F} \cdot d_{T}\right], [\boldsymbol{Y}]_{u}=\left[(\alpha+\beta) \cdot d_{T} \cdot d_{F}\right]_{u^{0}}。$ | (5) |
根据公式(2)和(3),可计算pu, b*=ru+$\frac{n_{T}}{d_{T}}$和pu, b**=ru+$\frac{n_{F}}{d_{F}}$。最终预测pu, b可以表示为
| ${p_{u, b}} = \frac{\beta }{{\alpha + \beta }} \cdot p_{u, b}^* + \frac{\alpha }{{\alpha + \beta }} \cdot p_{u, b}^{**} = {\bar r_u} + \frac{{\beta \cdot {n_T} \cdot {d_F} + \alpha \cdot {n_F} \cdot {d_T}}}{{(\alpha + \beta ) \cdot {d_T} \cdot {d_F}}} = {\bar r_u} + \frac{\mathit{\boldsymbol{X}}}{\mathit{\boldsymbol{Y}}}, $ |
服务提供商将结果发回给用户u,u解密后获得结果。
2.2 中心化的前n项预测协议与单预测协议类似,当用户想获取前n个未评分项目的评分时,进行如下协议。
服务提供商将PKu发送至随机选择且愿意参与计算的陌生人集Tu,陌生人t(t∈Tu)使用PKu和(Rt, Qt)计算[qt, b·(rt, b-rt)]u=Enc(PKu, qt, b·(rt, b-rt))和[2·qt, b]u=Enc(PKu, 2·qt, b),并将结果发回服务提供商。
用户u将加密后的权重[wu, f]u=Enc(PKu, wu, f)发送给每个朋友f∈Fu,好友f使用PKu、[wu, f]u和(Rf, Qf)计算
| $\left[q_{f, b}\right]_{u}=\sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(\cdot, {Enc}\left(P K_{u}, q_{f, i}\right), \left[\boldsymbol{I}_{b}^{(i)}\right]_{u}\right)\left[q_{f, b} \cdot\left(r_{f, b}-\bar{r}_{f}\right) \cdot w_{u, f} \cdot \sum\limits_{i=1}^{M} q_{f, i}\right]_{u}=\\ {Eval}\left(\cdot, {Enc}\left(P K_{u}, q_{f, b} \cdot\left(r_{f, b}-\bar{r}_{f}\right)\right), {Eval}\left(\cdot, \left[w_{u, f}\right]_{u}, \sum\limits_{1 \leqslant i \leqslant M} {Eval}\left(+, q_{f, i}\right)\right)\right), $ |
并将结果发回服务提供商。
用户u和服务提供商进行如下交互:用户u生成两个矩阵MX、MY,生成M·M单位矩阵; 随机置换列以获得MY; 对于每个项目b,若已被评分,则将MY第b列中的元素1替换为0,得到矩阵MX。用户u逐个元素加密矩阵,并将加密结果[MX]u、[MY]u发送到服务提供商,然后进行计算。
服务提供商首先按照单预测协议中的方法计算[nT]u、[dT]u、[nF]u、[dF]u、[X]u和[Y]u,然后根据公式(3)计算
| ${p_{u, b}} = \frac{\beta }{{\alpha + \beta }} \cdot \frac{{{n_{T, b}}}}{{{d_{T, b}}}} + \frac{\alpha }{{\alpha + \beta }} \cdot \frac{{{n_{F, b}}}}{{{d_{F, b}}}} = \frac{{\beta \cdot {n_{T, b}} \cdot {d_{F, b}} + \alpha \cdot {n_{F, b}} \cdot {d_{T, b}}}}{{(\alpha + \beta ) \cdot {d_{T, b}} \cdot {d_{F, b}}}} = \frac{{{\mathit{\boldsymbol{X}}_b}}}{{{\mathit{\boldsymbol{Y}}_b}}}。$ |
服务提供商置换密文向量(([X1]u, [Y1]u), ([X2]u, [Y2]u), …,([XM]u′[YM]u)):
| $\left(\left[\boldsymbol{U}_{1}\right]_{u}, \left[\boldsymbol{U}_{2}\right]_{u}, \cdots, \left[\boldsymbol{U}_{M}\right]_{u}\right)=\left[\boldsymbol{M}_{X}\right]_{u} \cdot\left(\left[\boldsymbol{X}_{1}\right]_{u}\left[\boldsymbol{X}_{2}\right]_{u}, \cdots, \left[\boldsymbol{X}_{M}\right]_{u}\right)^{\mathrm{T}}, \\ \left(\left[\boldsymbol{V}_{1}\right]_{u^{\prime}}\left[\boldsymbol{V}_{2}\right]_{u}, \cdots, \left[\boldsymbol{V}_{M}\right]_{u}\right)=\left[\boldsymbol{M}_{Y}\right]_{u} \cdot\left(\left[\boldsymbol{Y}_{1}\right]_{u^{\prime}}\left[\boldsymbol{Y}_{2}\right]_{u}, \cdots, \left[\boldsymbol{Y}_{M}\right]_{u}\right)^{\mathrm{T}}。$ |
元素之间的加法和乘法以同态运算函数的加法和乘法进行计算,密文矩阵和密文向量的乘法以标准方式进行。服务提供商使用密文上的比较协议,将Ui/Vi(1≤i≤|B|)进行排序。然后服务提供商将Top-n的索引发送给用户u,用户u解密后即可恢复真实的索引。
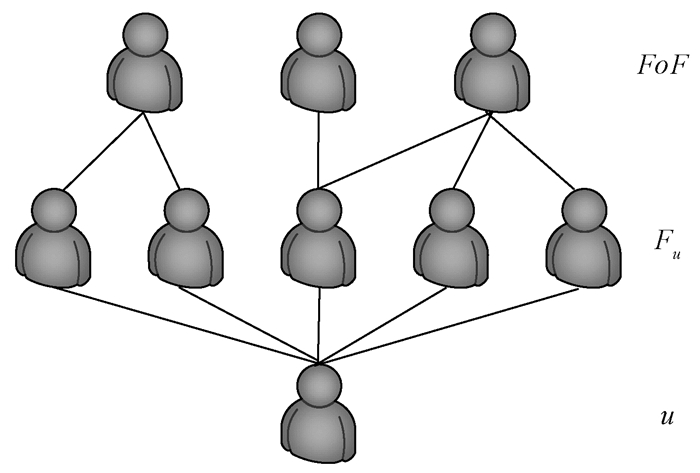
2.3 去中心化的预测协议半诚实的服务提供商往往是中心化的预测协议中的弱点,所以可以通过去除中心化的服务提供商,让用户之间进行沟通的方式来减少隐私泄露的可能性。假设所有用户在推荐算法中被唯一标记,并且用户之间共享社交网络图SG。在协议初始化阶段,用户u使用SHE方案生成其公私钥对(PKu, SKu)并公开其公钥以供他人验证。用户u生成其评级向量Ru和社交图SG,并为其每个朋友f∈Fu分配权重wu, f。其他用户也执行相同的操作。在本协议中,用户u的好友的好友(FoF)作为u的陌生人备选集合,系统结构的示意图如图 2。去中心化的预测协议计算如下。
|
图 2 去中心化的推荐算法结构图 Fig. 2 Structure of decentralized recommendation algorithm |
基于社交网络图SG,用户u选择一个由他的FoF组成的陌生人集合Tu,并在Tu中选择一个陌生人t′。u生成一个二进制向量Ib,其第b个元素为1,将该向量进行加密。并将加密结果[Ib]u=Enc(PKu, Ib)=([Ib](1)u, …, [Ib](M)u)连同[wu, f]u=Enc(PKu, wu, f)进行广播,发送给在Fu中的每一个好友。好友f使用PKu、[Ib]u、[wu, f]u和(Rf, Qf),通过类似中心化推荐算法的方式计算[qf, b]u和[qf, b·(Rf·Ib-rf)·wu, f]u,将结果发送给在Tu中的一个好友,同时也转发所收到的[Ib]u和PKu。对任意Tu中的陌生人t,都将从Fu中的好友处获得[Ib]u和PKu,并进行如下计算:①验证PKu;② t使用PKu和(Rt, Qt),计算[qt, b]u和[qt, b·(Rt·Ib-rt)]u;③ t根据已有的[qf, b]u和[qf, b·(Rf·Ib-rf)·wu, f]u,计算$\sum\limits_{f \in F_{u}}\left[q_{f, b}\right]_{u}$和$\sum_{f \in F_{u}}\left[q_{f, b} \cdot\left(\boldsymbol{R}_{f} \boldsymbol{I}_{b}-\bar{r}_{f}\right) \cdot w_{u, f} \cdot \sum_{i=1}^{M} q_{f, i}\right]_{u}$;④ t将②、③的计算结果发送给t′。
陌生人t′收到计算结果后,进行如下运算:
① 同中心化协议类似,计算[nT]u、[dT]u、[nF]u、[dF]u、[X]u和[Y]u;②计算得到结果。
2.4 安全性分析在基本安全模型中,假定服务提供者是半诚实的,将遵循协议规范并且不作为用户参与协议。此外,用户信任他的朋友是半诚实的。对于用户之间的通信信道,假设所有通信在完整性和机密性方面受到保护(具有前向保密性)。在最坏情况下的安全模型中,假设某些朋友可能会受到攻击。
本文中的推荐系统在两个模型中都是安全的,所有计算都是在用户u的公钥下以密文形式完成的,并且在协议中服务提供商不为SHE加密方案生成公私钥对,因此,协议避免了密钥恢复攻击。
在给定的安全模型中,推荐系统的信息泄露主要取决于参数α和β的大小以及陌生人集合的大小,若α/(α+β)增大,陌生人集合选择较小,则来自用户好友的信息比重更高,隐私信息更容易泄露。在协议中,用户u不与其他用户进行通信,因此u无法确定某特定用户是否参与计算;每次预测的陌生人集合都是随机选择,所以攻击者无法利用累积的信息进行攻击;用户的评分r∈{0, 1, 2, 3, 4, 5},因此已知的某个评分不能推断出该评分来自于哪个用户。
3 实验通过实验对本文所提出的改进与预测算法的准确性进行测试。数据集由MovieTweetings数据集构建而来(https://github.com/lux-jwang/Experiments/tree/master/code2016)。MovieTweetings为电影评分数据,本文所用测试数据集为FMT和10-FMT数据集,共包含359 908个评分、35 456个用户和20 156个条目。在FMT数据集中,每个用户至少有1个朋友,每个朋友至少有1个评级;在10-FMT数据集中,每个用户至少有10个朋友,每个朋友至少有10个评级。将每个数据集分为训练集和测试集,其中训练数据占80%,测试数据占20%。表 1和表 2描述了推荐算法在10-FMT数据集上的MAE值。软硬件环境为:系统为Ubuntu 18.04;处理器为Inter(R)Core(TM)i7-3610QM;内存为8 G。
|
|
表 1 中心化预测算法在10-FMT数据集中的MAE值 Tab. 1 The MAE of the centralized prediction algorithm in the 10-FMT data set |
|
|
表 2 去中心化预测算法在10-FMT数据集中的MAE值 Tab. 2 The MAE of the decentralized prediction algorithm in the 10-FMT data set |
首先在数据集中对算法的准确性进行测试。
从表 1和表 2中可以看出,推荐算法的MAE值随着好友用户参与的比重和用户好友集的增加而减少,预测准确度增加。相比于文献[8]方案,准确率有所提升。
将运算中常用的数据进行缓存,修改传递参数中一些多余的循环方式对代码进行优化,算法的运算效率提升如表 3、表 4所示。
|
|
表 3 数据处理阶段执行时间 Tab. 3 Data processing time |
|
|
表 4 算法运行阶段执行时间 Tab. 4 Algorithm execution time |
通过实验证明,协议中数据预处理过程和算法执行过程中的效率都得到提升,单预测协议运算时间减少了13.4%,Top-n协议运算时间减少了12.7%。
4 结束语本文构造并实现了一种准确高效的基于同态加密的隐私保护推荐协议,针对推荐算法中存在隐私泄露问题,在TW16方案基础上,增加活跃用户的评分权值提升推荐协议预测的准确性,对参数设置进行优化, 提升协议的效率,并对方案进行实验验证,结果表明推荐算法的准确性和效率均有所提升。今后可对本文的基础同态加密方案进行优化,进一步研究方案效率的提升。
| [1] |
KOBSA A. User modeling in dialog systems: potentials and hazards[J]. AI & society, 1990, 4(3): 214-231. (  0) 0) |
| [2] |
CASINO F, DOMINGO-FERRER J, PATSAKIS C, et al. A k-anonymous approach to privacy preserving collaborative filtering[J]. Journal of computer and system sciences, 2015, 81(6): 1000-1011. DOI:10.1016/j.jcss.2014.12.013 (  0) 0) |
| [3] |
BOUTET A, FREY D, GUERRAOUI R, et al. Privacy-preserving distributed collaborative filtering[J]. Computing, 2016, 98(8): 827-846. DOI:10.1007/s00607-015-0451-z (  0) 0) |
| [4] |
ELMISERY A M, BOTVICH D. An agent based middleware for privacy aware recommender systems in IPTV networks[C]//Proceedings of IEEE 6th International Design and Test Workshop. Beirut, 2011: 821-832.
(  0) 0) |
| [5] |
TANG Q, WANG J. Privacy-preserving context-aware recommender systems: analysis and new solutions[C]//Proceedings of 20th European Symposium on Research in Computer Security. Vienna, 2015: 101-119.
(  0) 0) |
| [6] |
张敏情, 李天雪, 狄富强, 等. 基于Paillier同态公钥加密系统的可逆信息隐藏算法[J]. 郑州大学学报(理学版), 2018, 50(1): 8-14. ZHANG M Q, LI T X, DI F Q, et al. Reversible data hiding algorithm based on Paillier homomorphic public key encryption system[J]. Journal of Zhengzhou university(natural science edition), 2018, 50(1): 8-14. (  0) 0) |
| [7] |
张薇, 白平, 李镇林, 等. 基于谓词的Paillier型密文解密外包方案[J]. 郑州大学学报(理学版), 2018, 50(3): 7-14. ZHANG W, BAI P, LI Z L, et al. Paillier type outsourcing the decryption ciphertexts via predicate encryption[J]. Journal of Zhengzhou university(natural science edition), 2018, 50(3): 7-14. (  0) 0) |
| [8] |
TANG Q, WANG J. Privacy-preserving friendship-based recommender systems[J]. IEEE transactions on dependable and secure computing, 2018, 15(5): 784-796. DOI:10.1109/TDSC.2016.2631533 (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


