异型组合拱桥是拱桥的一种特殊形式,其结构形式和力学性能与常规拱桥有一定差别[1-3].国内外学者对异型拱桥的静力学性能以及参数敏感性进行了大量的研究,但对于参数敏感性的分析主要集中在诸如矢跨比、拱肋倾角等结构构造方面,且由于异型拱桥的结构特异性,相互间不具有可借鉴性[4-10].本桥为V墩[11-12]异型钢混组合拱桥,现针对V墩预应力及吊杆力的变化,分析二者对该结构力学性能的影响,最终得到该桥力学行为对它们是否敏感.
1 工程概况及有限元建模 1.1 工程概况前程路大桥是位于郑州市贾鲁河与前程路交汇处的PC三角刚架异型梁拱组合桥.中跨桥面以上拱肋为钢结构,对应的主梁段也为钢结构.V墩及次边跨箱梁组成的刚构为混凝土结构.引桥为简支混凝土梁结构,以协调桥头的竖向位移,并作为防汛通道之用.
(1) 吊杆:纵向间距4.4 m;标准强度1 670 MPa,吊杆按一次张拉到位设计.
|
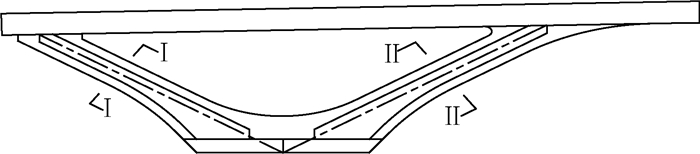
图 1 V型三角刚架构造 Figure 1 V-type triangular frame structure |
|
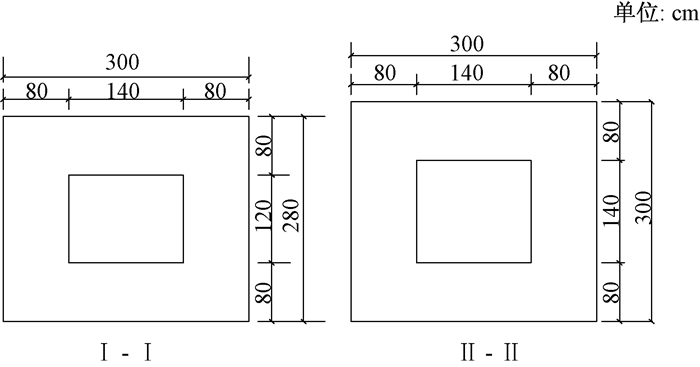
图 2 V墩截面构造 Figure 2 Section structure of V pier |
针对前程路大桥,采用Midas/FEA有限元软件建立有限元模型:大桥的混凝土梁以及V形墩采用3D实体单元进行模拟,钢拱肋和钢桥面板等采用2D板单元模拟,吊杆采用桁架单元进行模拟,实体单元与梁单元的连接通过共节点的方法进行耦合,预应力钢束选用1D钢筋单元模拟,钢筋单元和混凝土单元在划分单元时生成的节点处自动耦合.
1.2.1 预应力钢筋的建立采用线单元模拟预应力钢筋,首先建立每根预应力钢筋的线条模型,然后通过自动划分网格的方法生成钢筋单元,桥梁南半部分箱梁及V墩内的预应力筋有限元模型见图 3.

|
图 3 桥梁南侧箱梁及V墩内部的预应力筋有限元模型 Figure 3 Finite element model of prestressed tendons in the box girder and V-pier on the south side of the bridge |
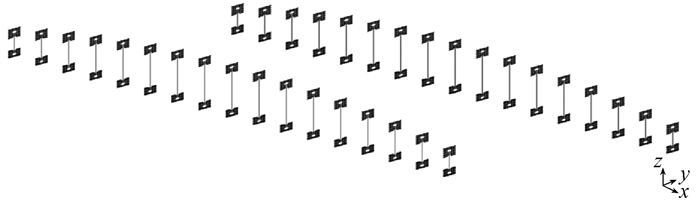
采用桁架单元模拟吊杆,共建立34个桁架单元,每根吊杆的两端分别与拱吊杆板和钢主梁吊杆板的板单元共节点,吊杆的有限元模型及其与拱肋和钢主梁的连接如图 4所示.
|
图 4 吊杆的有限元模型及其与拱肋和钢主梁的连接 Figure 4 Finite element model of the boom and its connection to the arch and the steel girders |
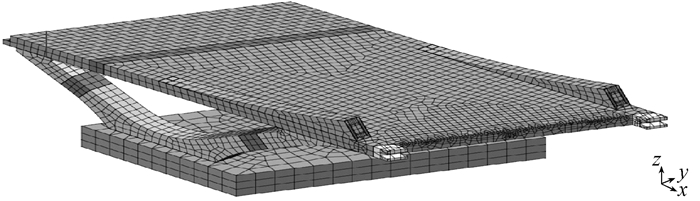
通过Midas/FEA中的布尔运算功能实现拱脚部分、混凝土箱梁、V墩以及承台的连接,三者的连接方式为固结,然后采用自动划分网格的方法划分成3D实体单元,桥梁南侧部位下部结构及混凝土桥面部分的有限元模型如图 5所示.
|
图 5 桥梁南侧混凝土部位的有限元模型 Figure 5 Finite element model of concrete location on the south side of bridge |
采用2D板单元模拟钢结构部分.首先建立单元面,相互焊接部位的单元面共用一个边线,共用的边线在网格划分之后用来模拟钢板之间的焊接连接,钢结构的有限元模型如图 6.

|
图 6 钢结构部分的有限元模型 Figure 6 Finite element model of steel structure |
本文PC混凝土的参数研究主要是V墩预应力参数研究.通过改变V墩预应力钢束的张拉控制力来分析该参数变化对钢结构部分受力和变形的影响.
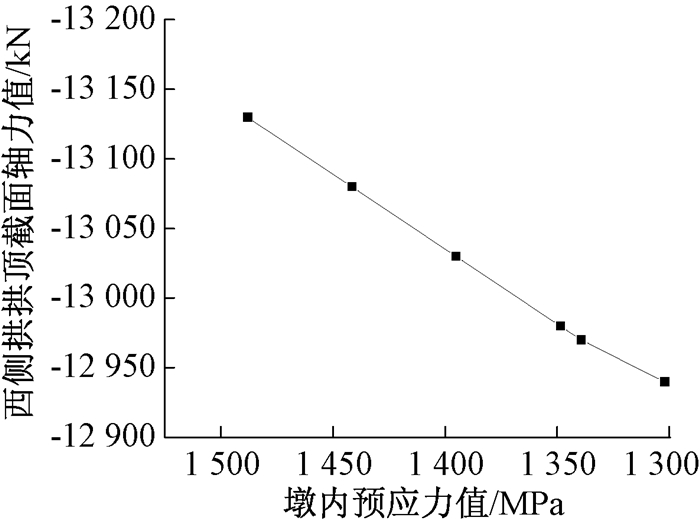
2.1.1 钢拱肋内力分析V墩预应力钢束的锚下控制应力值为1 339.2 MPa,规范要求预应力张拉控制应力在0.7~0.8 fcuk,其中,fcuk是混凝土立方抗压强度标准值.现取最大张拉控制应力值为1 448 MPa,并对实际运营过程中预应力可能出现损失现象进行模拟,分别取V墩预应力张拉控制应力为1 448、1 441.5、1 395、1 339.2、1 348.5、1 302 MPa,计算成桥状态下拱肋拱顶截面的内力值.东西两侧拱顶截面内力随V墩预应力的变化如图 7~9所示.
|
图 7 西侧拱顶截面轴力随V墩预应力值变化曲线 Figure 7 Curve of the prestressing force of the vault in the west side with the prestress of the V pier |
|
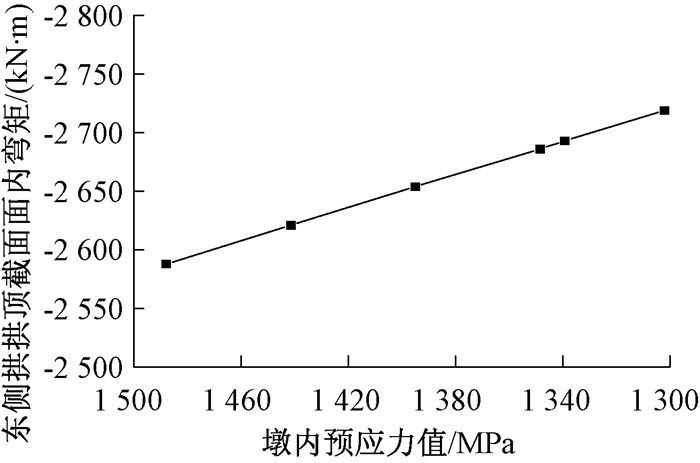
图 8 东侧拱顶截面面内弯矩随V墩预应力值变化曲线 Figure 8 Curve of the prestressed moment of the vault in the east side with the prestress of the V pier |
|
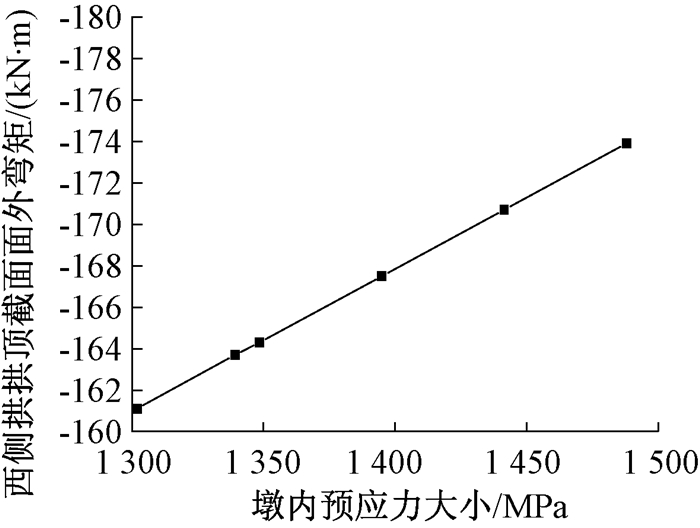
图 9 西侧拱顶截面面外弯矩随V墩预应力变化曲线 Figure 9 Curve of the outer bending moment of the vest in the west side with the prestress of the V pier |
由图 7~9可知,V墩预应力值在1 302~1 488 MPa之间变化时可得以下规律:
(1) V墩预应力大时,拱顶截面轴力值大,因V墩预应力张拉力大时,V型桥墩受预应力影响变形的同时,受V型桥墩变形影响钢拱肋沿拱轴线方向会产生挤压变形,导致承受的压力值增大.但是拱肋承受的压力仅变化1.2%,可认为拱顶截面轴力对V墩预应力变化不敏感.
(2) 随V墩预应力值变化,面内弯矩的变化呈现出以下现象:东侧拱肋拱顶截面面内弯矩变小,西侧拱拱顶截面面内弯矩变大,两侧拱肋拱顶截面面内弯矩变化呈现出不同的变化规律,体现出异型拱桥内力变化的特异性.由于预应力的变化引起V型桥墩不同的变形,进而产生拱肋弯矩的不同变化.东侧拱肋由V型桥墩变形引起的弯矩方向与拱肋自重和吊杆力引起的弯矩方向相反,故东侧拱肋弯矩减小.西侧拱肋由V型桥墩变形引起的弯矩方向与拱肋自重和吊杆力引起的弯矩方向一致,故西侧拱肋弯矩增大.东侧拱肋拱顶截面的面内弯矩随V墩预应力的增大而减小4%,可认为拱顶截面面内弯矩对V墩预应力变化敏感.
(3) V墩预应力值由1 339.2 MPa变化至1 488 MPa时,两侧拱顶截面面外弯矩均变大.此桥为异型斜拱桥,由于V墩预应力的张拉导致拱肋更容易产生侧倾效应,此时拱顶截面的面外弯矩值增大,面外弯矩的变化率为6.2%,可认为拱顶截面面外弯矩对V墩预应力变化敏感.
2.1.2 钢拱肋变形分析拱肋变形以拱顶截面挠度最具代表性,因此本文对拱肋变形的研究均为拱顶截面挠度.
分析表 1可知:V墩预应力值增大时,截面最大挠度值由3.72 cm增大至3.79 cm.这是由于一次成桥分析时V墩预应力的张拉导致拱肋下挠,张拉力越大则拱肋下挠越明显.但拱顶截面挠度增大率仅为1.9%,可认为拱顶截面挠度对V墩预应力的变化不敏感.
|
|
表 1 拱顶截面挠度值随V墩预应力变化表 Table 1 The deflection value of the vault section changes with the prestress of the V pier |
由表 2可得,随着V墩预应力值减小,钢主梁跨中挠度值递减.因为V墩预应力减小时,V型墩受到的挤压效应减弱,V型墩的竖向变形减小,然后与V墩相连的上部结构的竖向变形也减小.但V墩预应力变化时,挠度值变化率仅为2%,故挠度对V墩预应力变化不敏感.
|
|
表 2 钢主梁跨中斜截面最大挠度值随V墩预应力值变化表 Table 2 Variation of the maximum deflection value of the cross-section of the steel girder with the V pier |
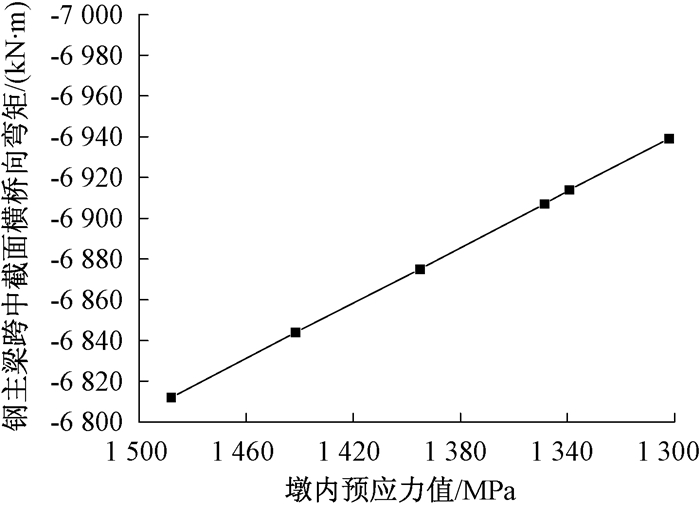
以钢主梁跨中截面内力值为研究对象,其随V墩预应力变化而变化如图 10~13所示.
|
图 10 钢主梁跨中截面横桥向弯矩随V墩预应力变化曲线 Figure 10 Curve of prestressed bending moment of V pier of cross-section of steel girder |
|
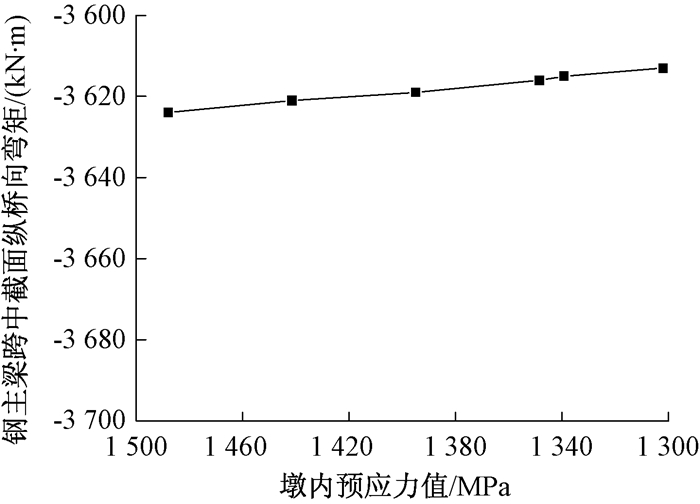
图 11 钢主梁跨中截面纵桥向弯矩随V墩预应力变化曲线 Figure 11 Curve of prestressing moment of longitudinal bridge moment with V piers of steel main girder cross section |
|
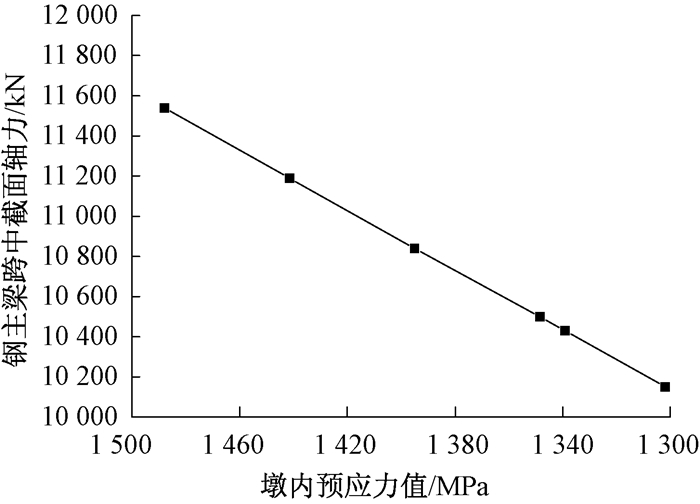
图 12 钢主梁跨中截面轴力随V墩预应力变化曲线 Figure 12 Curve of prestressing force of cross section of steel main girder with V pier |
|
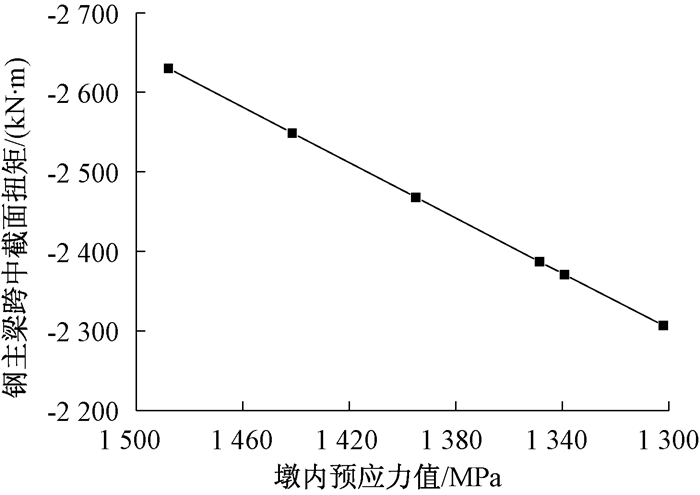
图 13 钢主梁跨中截面扭矩随V墩预应力应力值变化曲线 Figure 13 Curve of prestressed stress value of cross section of steel main girder with V pier |
(1) V墩预应力值增大时,钢主梁跨中截面弯矩减小.原因是V墩预应力增大时,V型桥墩的变形对墩梁结合部位产生的弯矩与钢主梁的自重、二期荷载产生的弯矩方向相反,所以钢主梁的弯矩减小.但变化率仅为1.5%,可认为钢主梁跨中截面横桥向弯矩对V墩预应力的变化不敏感.
(2) 此异型组合结构拱桥的钢主梁部分存在扭转现象.V墩预应力钢束张拉力会使结构扭转加大,因此钢主梁跨中截面的纵桥向弯矩及跨中截面扭矩均增大.V墩预应力增大过程中,钢主梁跨中截面扭矩值增大11%,纵桥向弯矩变化率仅为0.3%,所以钢主梁跨中截面纵桥向弯矩对V墩预应力的变化不敏感,跨中截面的扭矩值对V墩预应力的变化敏感.
(3) 随着V墩预应力值的减小,钢主梁跨中截面的轴力值减小,原因是V型桥墩因预应力的张拉而产生沿桥梁纵向变形,V墩预应力值减小时,桥墩沿桥梁纵向的变形减小.桥墩沿桥梁纵向的变形对钢主梁产生一种张拉效应,所以钢主梁的拉力减小,同时钢主梁跨中位置的挠度值减小.V墩预应力减小过程中,钢主梁跨中截面的拉力由11 540 kN减小至10 430 kN,此时拉力变化率为10.6%,可认为钢主梁跨中截面轴力对V墩预应力的变化敏感.
2.1.5 钢主梁应力分析由表 3可知,随着V墩预应力值增大过程中,最大应力由17.7 MPa变化至18.2 MPa.此时钢主梁跨中位置的扭转及弯曲效应均有所增大,但是增大的幅度不明显,而且跨中部位的应力值变化率仅为2.8%,可认为钢主梁跨中斜截面应力对V墩预应力的变化不敏感.
|
|
表 3 钢主梁跨中斜截面最大应力值随V墩预应力值变化表 Table 3 Variation of the maximum stress value of the mid-span oblique section of the steel girders with the prestressing stress value of the V pier |
假定吊杆力的变化不会引起拱结构的合理拱轴线变化,在其他参数不变的情况下,单纯地改变吊杆力的大小研究其中的规律.
2.2.1 钢拱肋内力分析以原始设计吊杆力为参照,现将吊杆力由增大5%逐步增大至20%,计算成桥状态下拱肋拱顶截面的内力值,数据如图 14~16所示.
|
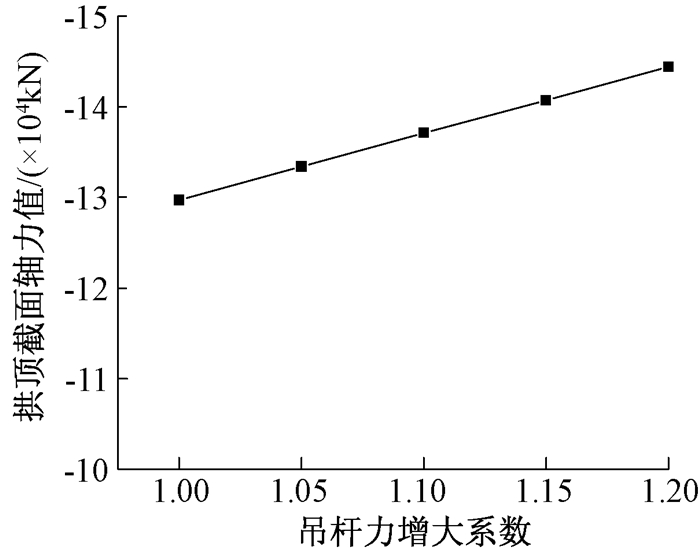
图 14 西侧拱顶截面轴力随吊杆力变化曲线 Figure 14 Curve of axial force on the west dome cross section with the boom force |
|
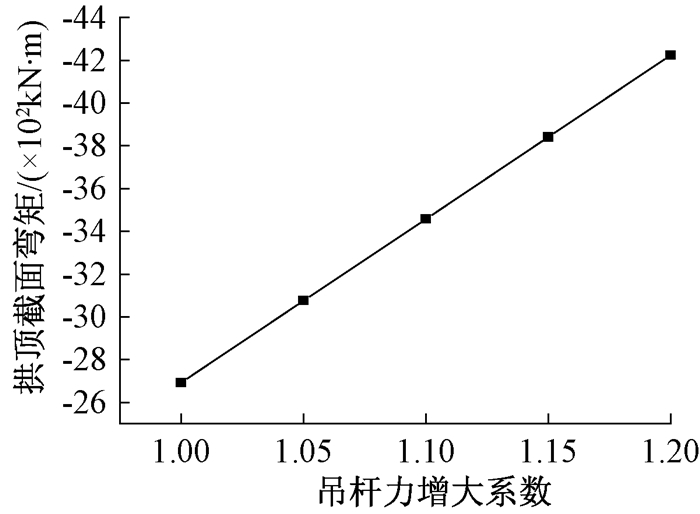
图 15 东侧拱顶截面面内弯矩随吊杆力变化曲线 Figure 15 Curve of the moment of the arch in the east side of the arch |
|
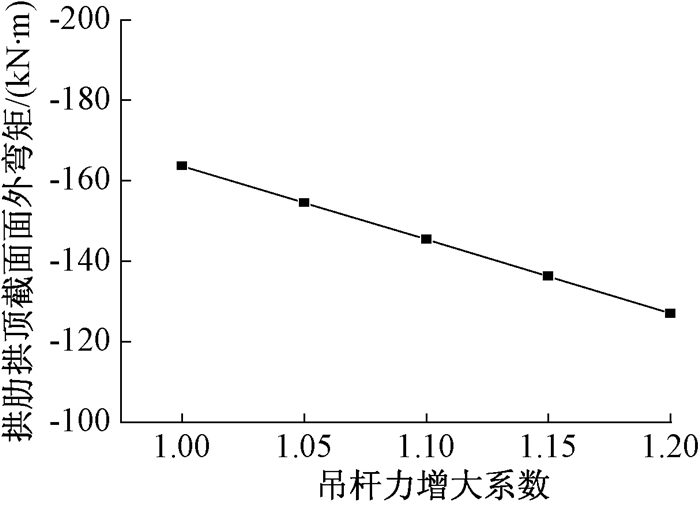
图 16 西侧拱顶截面面外弯矩随吊杆力变化曲线 Figure 16 Curve of the boom at the outer side of the dome |
可见东侧拱拱顶及西侧拱拱顶截面面内弯矩变化规律不一致,因此对二者进行单独分析.
(1) 吊杆力增大时,拱顶截面压力增大.钢拱肋作为一种主要承受压力的构件,同时承受自重及吊杆的张拉力作用.当吊杆力增大时,钢拱肋承受的压力就会增大.吊杆力增大20%时,拱顶截面压力值增大11.3%,可认为拱顶截面压力对吊杆张拉力变化敏感.
(2) 吊杆力增大时,东侧拱顶截面面内弯矩增大,西侧拱拱顶面内弯矩减小.东侧吊杆的张拉力引起的弯矩与原弯矩方向一致,所以导致弯矩增大,而西侧拱由吊杆的张拉力引起的弯矩与原弯矩方向相反,所以西侧拱顶截面面内弯矩随吊杆力的增大而减小.吊杆力增大20%时,东侧拱肋拱顶截面面内弯矩增大56.9%,故拱顶截面面内弯矩对吊杆力变化敏感.
(3) 吊杆力增大时,西侧拱肋拱顶截面面外弯矩由-163.7 (kN ·m)变化至-127 (kN ·m),吊杆力增大20%,拱顶截面面外弯矩减小22.4%,可认为拱顶截面面外弯矩对吊杆力变化敏感.
2.2.2 钢拱肋应力分析以拱顶截面最大应力值为研究对象,分析拱顶截面应力最大值随吊杆力变化情况.
由表 4可知,吊杆力的设计值增大至1.2倍时,拱顶截面应力最大值增大.吊杆力增大时拱顶截面轴力及剪力增大,而此时拱顶截面面积并未发生变化,所以是截面应力增大.拱顶截面吊杆力增大20%,拱顶截面应力最大值增大21.7%,拱顶截面应力对吊杆力变化敏感.
|
|
表 4 拱顶截面应力值随吊杆力变化表 Table 4 Varical stress values of vaults |
以拱顶截面最大挠度值为研究对象,分析拱顶截面挠度值随吊杆力变化情况.
由表 5可知,吊杆力的设计值增大至1.2倍时,拱顶截面挠度最大值由3.72 cm增大至4.4 cm.吊杆力增大时对拱肋的拉力随之增大,而拱肋抗弯刚度不变,则挠度增大.吊杆力增大20%,拱顶截面挠度最大值增大18.3%,所以拱顶截面挠度对吊杆力变化敏感.
|
|
表 5 拱顶截面挠度值随吊杆力变化表 Table 5 Variation of vaulting section deflection value |
以钢主梁跨中截面内力值为对象,分析吊杆力设计值增大时钢主梁跨中截面内力变化.
由表 6可知:
|
|
表 6 钢主梁跨中截面内力值随吊杆力变化表 Table 6 Variation of the internal force of the cross section of the steel girders |
(1) 钢主梁跨中截面横桥向弯矩值呈现出先减小后增大的趋势.吊杆是影响钢主梁受力和变形的重要传力构件,吊杆力增大会引起钢主梁内力重分配.当吊杆力变化较大时,横桥向弯矩值发生很大的变化,可认为钢主梁跨中截面横桥向弯矩对吊杆力的变化敏感.
(2) 钢主梁跨中截面纵桥向弯矩值呈现出逐渐减小的趋势.由于吊杆力的增大,主梁扭转效应减弱,导致纵桥向弯矩值减小.吊杆力增加20%,钢主梁跨中截面纵桥向弯矩值减小55%,可认为钢主梁跨中截面纵桥向弯矩对吊杆力的变化敏感.
(3) 钢主梁跨中截面扭矩值呈现出先减小后增大的趋势.对斜桥而言,跨中截面的扭矩主要由钢主梁自重及二期恒载引起.当吊杆力小幅增大时,吊杆将更多的力传递给拱肋,因此钢主梁自重和二期恒载引起的扭矩就会减小.当吊杆力的总和超过钢主梁自重及二期恒载的和并且继续增大时,扭矩的方向就会发生变化而且随吊杆力变化趋势同步增大,可认为钢主梁跨中截面扭矩对吊杆力的变化敏感.
(4) 钢主梁跨中截面的轴力随吊杆力增大而增大.吊杆力增大时钢拱肋轴力增大,那么拱肋与主梁结合部位对主梁的作用力的水平分力就增大.吊杆力变化20%,钢主梁跨中截面轴力值变化38.4%,可认为钢主梁跨中截面轴力对吊杆力的变化敏感.
2.2.5 钢主梁变形分析以钢主梁跨中截面最大挠度值为研究对象,分析拱顶截面挠度值与随吊杆力变化情况.
由表 7可知:吊杆力的设计值增大时,钢主梁跨中截面挠度最大值减小.吊杆力作为传力构件影响钢主梁的受力和变形,吊杆力增大时对钢主梁的竖向拉力也增大,此拉力平衡一部分钢主梁的自重及二期恒载,所以钢主梁的挠度就会降低.吊杆力增大20%,钢主梁跨中截面挠度最大值减小88%,可认为钢主梁跨中截面挠度对吊杆力变化敏感.
|
|
表 7 拱顶截面挠度值随吊杆力变化表 Table 7 Dome section deflection values hinge force change table |
(1) V墩预应力增大时:拱顶截面面外弯矩、钢主梁跨中截面轴力、钢主梁跨中截面纵桥向弯矩、钢主梁跨中截面扭矩增大.
(2) 吊杆力增大时:拱顶截面轴力、东侧拱拱顶截面面内弯矩、拱顶截面应力、拱顶截面的挠度、钢主梁跨中截面轴力增大.拱顶截面面外弯矩、西侧拱拱顶截面面内弯矩、钢主梁跨中截面横桥向弯矩、钢主梁跨中截面纵桥向弯矩、钢主梁跨中截面挠度减小.跨中截面横向弯矩以及扭矩呈现出先逐渐减小然后方向发生变化并且数值逐渐增大的变化规律.
(3) V墩预应力、吊杆张拉力为影响结构静力力学性能的敏感参数.适当增大吊杆张拉力能够明显减小跨中截面的挠度值.
| [1] |
李生智, 王玮瑶, 邬妙年. 异型拱桥[M]. 北京: 人民交通出版社, 1996.
(  0) 0) |
| [2] |
李刚. 异型拱桥的结构分析与研究[D]. 西安: 长安大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009210719.htm
(  0) 0) |
| [3] |
李乔, 李丽. 异型拱桥结构内力分析[J]. 公路交通科技, 2001, 18(1): 31-35. (  0) 0) |
| [4] |
刘春凤, 司秀勇, 蒋再松, 等. 钢系杆拱桥结构体系设计参数研究[J]. 世界桥梁, 2008(s1): 64-67. (  0) 0) |
| [5] |
李莹, 孙海涛, 孙斌. 无推力斜靠式拱桥设计参数研究[J]. 上海应用技术学院学报(自然科学版), 2009, 9(4): 286-290. (  0) 0) |
| [6] |
陈峰, 贺拴海, 胡大琳, 等. 钢管混凝土斜靠式拱桥力性能及参数分析[J]. 广西大学学报(自然科学版), 2011, 36(1): 107-112. (  0) 0) |
| [7] |
冯云成. 上承式预应力混凝土刚性梁柔性拱桥静力分析[J]. 世界桥梁, 2012, 40(1): 47-19, 64. (  0) 0) |
| [8] |
李晓林. 异型拱桥静力特性及施工分析[D]. 合肥: 合肥工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10359-1012521745.htm
(  0) 0) |
| [9] |
周鹏. 斜跨拱桥结构静力性能研究[D]. 大连: 大连理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1014154549.htm
(  0) 0) |
| [10] |
周莉, 孙东利, 谢斌, 等. 钢-混组合体系—中承式系杆拱桥的设计[J]. 城市道桥与防洪, 2012(6): 109-113. (  0) 0) |
| [11] | |
| [12] |
石飞停, 甘亚南, 张杨永. V墩连续刚构桥受力性能的参数分析研究[J]. 淮阴工学院学报, 2015, 24(5): 57-59. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


