2. 河南省高校计算智能与数据挖掘工程技术研究中心 河南 新乡 453007
2. Engineering Technology Research Center for Computing Intelligence and Data Mining of Henan Province, Xinxiang 453007, China
肿瘤的致病机理复杂且难以治愈,给人类的健康带来巨大的威胁.《2015年中国癌症统计数据》指出,我国癌症的发病率和死亡率越来越高,基因微阵列技术为癌症的诊断和治疗提供了新途径[1].基因表达谱数据的样本维度高、样本量小等特性为特征基因选择带来了困难[2].文献[3]指出,基因表达谱分类问题重在特征选择的方法,而非分类器的选择.因此,特征基因选择方法成为研究的关键.文献[4]提出了一种用于癌症分类的过滤特征选择方法,该方法使用相关系数的排序来提取出与癌症相关的基因.文献[5]用递归特征消除方法进行特征基因选择.因基因表达谱具有高维、低样本、冗余多等特点,使得这些选择模型存在计算时间复杂度高和正确识别率不高等问题.文献[6]在粗糙集模型基础上提出邻域粗糙集特征选择的模型,在敏感特征选择方面取得较好的效果.在该方法中,邻域的大小是跟阈值的设置直接相关的,阈值的不同设置,直接影响着最终的分类精度和提取的特征基因数[7].近年来一些学者针对邻域选择进行了很多研究.文献[8]提出了基于标准差计算邻域的粗糙集模型,对输送带缺陷电磁查验信号进行仿真试验.文献[9]采用非对称结构的邻域形式,得到了较好的分类结果.目前,邻域粗糙集模型采用全局定邻域的形式,但数据复杂多变,目前这些邻域取值方式不能对数据进行精确的描述,分类结果会随着邻域的改变产生较大的差异,进而影响算法的稳健性.
本文基于主成分分析(PCA)和改进邻域粗糙集(NRS)的理论,研究了特征基因的选择问题,构造了基于PCA和NRS的PNRS模型.首先采用PCA方法得到低维特征空间,减少计算邻域的时间复杂度.多邻域粗糙集算法采取集合邻域半径,即为每个基因计算不同的邻域值,这种计算方式可提升对数据分布的描述能力.然后利用顺序向前的启发式搜索算法,保证了重要度较大的属性不被删除,选择得到最优或者较优的特征基因子集,提高模型的分类精度.针对标准的基因数据集,验证了PNRS模型的有效性.结果表明,PNRS模型可选择较小的特征基因子集,与其他相关方法对比,在分类精度等方面都有较好的表现.
1 基本概念 1.1 主成分分析主成分分析(PCA)是一种统计学方法,其基本原理是通过少数几个主成分来揭示多个变量间关系,即从原始变量中选择出少数几个主成分,使它们尽可能多地保留原始变量的信息,且彼此间互不相关[10].
1.2 邻域粗糙集文献[6]提出的邻域粗糙集模型在解决数值型问题时表现出了较优的特性.
定义1[6] 在给定的N维实数空间Ω中,I为实数集,IN为N维实数向量空间,M=IN×IN→I,则M称为IN上的一个度量.
定义2[6] 在给定实数空间Ω上的非空有限集合U={x1, x2, …,xn},对∀xi的邻域δ定义为δ(xi)=(x|x∈U, Δ(x, xi)≤δ),其中δ≥0.
定义3[6] 给定一非空有限集合U={x1, x2, …,xn},A是表述U的实数型特征集合,D是决策属性,如果A生成论域上的一族邻域关系,则称NDS=〈U, A∪D〉为一邻域决策系统.
定义4[6] 给定一邻域决策系统NDS=〈U, A∪D〉,决策属性D将论域U划分为N个等价类(X1, X2, …,XN),∀B⊆A,则决策属性D关于子集B的上近似和下近似分别为
| $ {{\bar{N}}_{B}}D=\cup _{i=1}^{N}{{\bar{N}}_{B}}{{X}_{i}}, $ | (1) |
| $ {{\underline{N}}_{B}}D=\cup _{i=1}^{N}{{\underline{N}}_{B}}{{X}_{i}}, $ | (2) |
式中:
同样可得决策系统的边界为
| $ BN\left( D \right)={{\bar{N}}_{B}}D-{{\underline{N}}_{B}}D, $ | (3) |
邻域粗糙集的正域为
| $ Po{{s}_{B}}\left( D \right)={{\underline{N}}_{B}}D, $ | (4) |
邻域粗糙集的负域为
| $ Ne{{g}_{B}}\left( D \right)=U-{{\bar{N}}_{B}}D, $ | (5) |
决策属性D对条件属性B的依赖度为
| $ {{k}_{D}}={{\gamma }_{B}}\left( D \right)=\frac{\left| Po{{s}_{B}}\left( D \right) \right|}{\left| U \right|}. $ | (6) |
定义5[6] 条件属性a和条件属性集B对于决策属性D的重要度SIG公式为
| $ SIG\left( a, B, D \right)={{\gamma }_{B\cup \{a\}}}\left( D \right)-{{\gamma }_{B}}\left( D \right), $ | (7) |
式中:a为条件属性;B为条件属性集;D为决策属性.
2 PCA和多邻域粗糙集的特征基因选择方法 2.1 欧氏距离的多邻域计算本文算法从特征选择方法模型泛化的角度考虑,选用欧氏距离函数作为计算基因数据间相似程度的度量,并且能解决过拟合问题,是处理实数型数据较为常用的方法.
定义6 给定一个决策表DT=(U, C∪D, {Va}, fa) a∈C,任意两点x, y∈U在特征子集R⊆C上的欧氏距离Δ(x, y, R)为
| $ \mathit{\Delta} \left( x, y, R \right)=\sqrt{\sum\limits_{a\in R}{{{({{f}_{a}}\left( x \right)-{{f}_{a}}\left( y \right))}^{2}}}}. $ | (8) |
在特征基因子集R中,采用的基于欧氏距离的多邻域计算,需要针对每个属性计算邻域,用于构建邻域集合.则基于欧氏距离的多邻域定义为
| $ L_{R}^{\mathit{\Delta} }\left( x \right)=\left\{ y|y\in U, \mathit{\Delta} \left( x, y, \{a\} \right)/r \right\}, $ | (9) |
式中:a∈R;r为计算邻域设定的参数.
2.2 PCA和多邻域粗糙集的肿瘤特征基因选择方法采用PCA算法对基因表达谱数据构建新的低维特征空间,并将改进的邻域粗糙集应用于特征基因的选择,以便提取的特征基因子集能较大程度地维持原数据集的分类性能.基于PCA和多邻域粗糙集的肿瘤特征基因选择算法描述见算法1.
算法1 基于PCA和多邻域粗糙集的肿瘤特征基因选择算法.
输入:基因数据集S=(x1, x2, …, xN), 邻域决策系统NDS=〈U, A∪D〉,计算属性邻域半径的参数r及属性的重要度下限参数β;
输出:特征基因集合SD.
Step 1:首先采用PCA算法对基因数据集S降维处理,选取贡献率η大于1%的基因数据集SA.
Step 2:初始化约简集合red=
Step 3:计算属性ai邻域δ(xi)=Δ(xi)/r.
Step 4:对SA中的ai∈SA-red;//ai表示特征基因集合SA的属性列.
Step 5:计算ai的正域及其重要度SIG.
Step 6:获取属性ai的正域集合Posk(D).
Step 7:判断重要度SIG是否大于设定的下限β.
Step 8:若SIG≤β,记录k值,red=red+ak,SA=SA-Posk,返回Step 7;若SIG>β,输出约简结果red.
Step 9:根据red对应的属性,获取较优的特征基因集合SD.
Step 10:结束.
3 实验分析 3.1 数据集为了验证该算法的有效性,在Leukemia、Colon Tumor、Lung Cancer、Prostate Cancer 4个公开的基因表达谱数据集进行仿真实验,前2个数据集从(http://featureselection.asu.edu/datasets.php)下载,后2个数据集从(http://datam.i2r.a-star.edu.sg/datasets/krbd/)下载,实验选用的4个数据集均为用于测试的两分类数据集,其详细信息如表 1所示.
|
|
表 1 数据集信息 Table 1 Description of datasets |
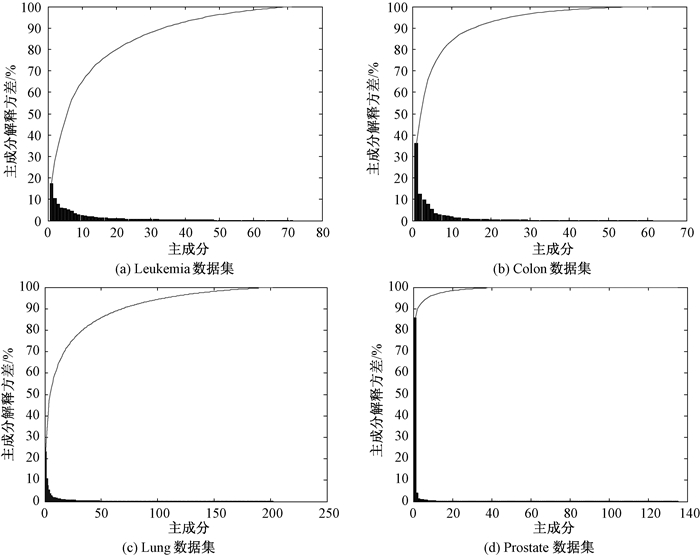
为了减少计算多邻域粗糙集模型的时间复杂度,先采用PCA算法对4个基因表达谱数据进行特征提取,并对提取的候选特征基因子集绘制各主成分解释方差的帕累托图,结果如图 1所示.
|
图 1 数据集各主成分解释方差的帕累托图 Figure 1 Pareto diagram of the principal components explained variance on datasets |
由图 1可以看出,实验的4个基因表达谱数据,当基因属性个数为50时,其贡献率多数可达90%以上,Lung在70个主成分时,贡献率达到90%以上.为了避免一定程度上的基因信息丢失,使得所提取的特征基因子集能最大限度地保持原数据集的分类能力,选取主成分贡献率大于1%的主成分,将它们应用于特征基因的提取中.
在邻域粗糙集模型的基础上,对邻域半径的选取进行了优化,经过多次试验比较,邻域阈值r的取值在区间[0, 2]上较为合适,不同的基因数据分别设置不同的阈值r.重要度下限β取值较小,本文取β=0.01.通过以上处理,筛选出了分辨能力强、冗余度较低的特征基因,筛选后的特征基因数目及对应的阈值取值如表 2所示.
|
|
表 2 特征基因数目及对应的阈值取值 Table 2 The number of feature genes and the corresponding threshold values |
为了检验所提出的PNRS算法对基因数据处理的有效性,从以下2个方面对选择得到的特征基因的分类能力进行检验.
1) 分类器
为了验证所提出模型的分类性能,使用Weka工具里几种常用的分类器对基因数据进行分类验证,并与直接对原始数据进行分类测试的方法进行对比.实验均采用十折交叉方法进行验证,结果如表 3所示.
|
|
表 3 不同分类器的分类精度对比 Table 3 Performance comparison of different classifiers on datasets |
从表 3可以看出,本文算法选择得到的特征基因子集对致病组织和正常组织样本表现出了良好的分类性能.比如白血病数据采用Lib-SVM分类,分类精度从65.27%增加到了100.0%,准确率提高了34.73%,从而说明本文的PNRS模型可行有效.
2) 基因选择方法
实验选取了一些单一的特征选择方法和学者提出或改进的相关算法进行对比实验.本文PNRS算法与ODP(original data processing)、PCA和NRS特征提取的方法进行对比,为保证对比实验的可行性和有效性,NRS的阈值设置与本文的PNRS模型阈值设置一致.另外,与文献[11]的BQPSO算法、文献[12]的IGA算法以及文献[13]的GSIL算法进行特征选择对比.采用Weka工具里的Lib-SVM分类器进行仿真实验,结果如表 4所示,各方法提取的特征基因数目如表 5所示.
|
|
表 4 不同基因选择方法的分类精度对比 Table 4 Performance comparison of different algorithms on datasets |
|
|
表 5 不同基因选择方法提取的特征基因数目 Table 5 The number of feature genes in different algorithms on datasets |
由表 4可以看出,采用ODP方法测试的准确率最低.例如Prostate基因数据集,ODP方法测试的准确率为56.61%,相比PCA方法的65.41%、NRS方法的69.87%、BQPSO方法的99.25%、IGA方法的98.82%、GSIL方法的96.08%以及本文PNRS方法的99.41%均偏低,表明原基因表达谱数据集中含有较多冗余信息,相比另外几种方法都采用特征基因选择的过程,说明在去除冗余噪声的基因后,提高了基因的分类能力,较多特征基因并不会提高模型的分辨能力.
从表 4、表 5可以看出,与PCA、NRS算法相比,PNRS模型提取的特征基因个数较少,并且基因测试的准确率均有大幅度提高.对比BQPSO、IGA、GSIL算法,虽然个别方法的准确率比本文的PNRS模型偏高,但是它们选择的特征基因数量较多,例如Lung数据集采用BQPSO、IGA、GSIL模型的准确率均比PNRS模型偏高,但是它们选择出的特征基因数目分别为10、14、7,比PNRS模型选择出的6个特征基因子集偏多.综合来看,本文提出的PNRS模型在分类准确率上高于BQPSO、IGA、GSIL等算法,并且选择出的特征基因子集的数目较少,验证了本文提出的特征选择模型的有效性.
4 小结PCA可以删除关系紧密的变量,提取出较少的特征变量,NRS约简算法可以有效地进行特征选择.本文根据基因表达谱的空间分布特点,首先采用PCA获得低维的特征空间,减小计算的时间复杂度;然后利用多邻域粗糙集算法,采用欧氏距离对每列属性计算邻域值,根据邻域集合来计算近似;最后采用启发式搜索选择出特征基因子集.与邻域粗糙集模型相比,采用多邻域的形式能够对数据进行更加精确的描述.结果表明,本文的PNRS算法选择出了较少的特征基因,且得到了较高的分类精度.
| [1] |
CHEN W, ZHENG R, BAADE P D, et al. Cancer statistics in China, 2015[J]. CA Cancer J Clin, 2016, 66(2): 115-132. DOI:10.3322/caac.21338 (  0) 0) |
| [2] |
徐天贺, 马媛媛, 徐久成. 一种基于邻域互信息最大化和粒子群优化的特征基因选择方法[J]. 小型微型计算机系统, 2016, 37(8): 1775-1779. (  0) 0) |
| [3] |
SCHÖLKOPF B, TSUDA K, VERT A. Gene expression analysis: joint feature selection and classifier design[M]. Cambridge: MIT Press, 2004.
(  0) 0) |
| [4] |
GOLUB T R, SLONIM D K, TAMAYO P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring[J]. Science, 1999, 286(2): 531-537. (  0) 0) |
| [5] |
FURLANELLO C, SERAFINI M, MERLER S, et al. Entropy-based gene ranking without selection bias for the predictive classification of microarray data[J]. BMC bioinformatics, 2003, 4(1): 54-59. DOI:10.1186/1471-2105-4-54 (  0) 0) |
| [6] |
胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报, 2008, 19(3): 640-649. (  0) 0) |
| [7] |
黄德双. 基因表达谱数据挖掘方法研究[M]. 北京: 科学出版社, 2009.
(  0) 0) |
| [8] |
毛清华, 马宏伟, 张旭辉. 改进邻域粗糙集的输送带缺陷特征约简算法[J]. 仪器仪表学报, 2014, 35(7): 1676-1680. (  0) 0) |
| [9] |
惠景丽, 潘巍, 吴康康, 等. 基于非对称变邻域粗糙集模型的属性约简[J]. 计算机科学, 2015, 42(6): 282-287. DOI:10.11896/j.issn.1002-137X.2015.06.059 (  0) 0) |
| [10] |
MANJÓN J V, COUPÉ P, BUADES A. MRI noise estimation and denoising using non-local PCA[J]. Medical image analysis, 2015, 22(1): 35-47. DOI:10.1016/j.media.2015.01.004 (  0) 0) |
| [11] |
XI M, SUN J, LIU L, et al. Cancer feature selection and classification using a binary quantum-behaved particle swarm optimization and support vector machine[J]. Computational and mathematical methods in medicine, 2016, 12(9): 1-9. (  0) 0) |
| [12] |
范方云, 孙俊, 王梦梅. 一种基于改进的遗传算法的癌症特征基因选择方法[J]. 江南大学学报(自然科学版), 2015, 14(4): 413-418. (  0) 0) |
| [13] |
张靖, 胡学钢, 李培培, 等. 基于迭代Lasso的肿瘤分类信息基因选择方法研究[J]. 模式识别与人工智能, 2014, 27(1): 49-59. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


