2. 谢菲尔德大学 土木与结构学院 谢菲尔德 S13JD 英国;
3. 河海大学 工程力学系 江苏 南京 210098
2. Department of Civil and Structural Engineering, University of Sheffield, Sheffield S13JD, UK;
3. Department of Engineering Mechanics, Hohai University, Nanjing 210098, China
混凝土是由嵌埋于水泥砂浆中的不同粒径的骨料颗粒,以及微孔隙和微缺陷构筑而成的多相复合材料.混凝土内部结构导致它在宏观尺度上显示出与其他晶体材料截然不同的力学性能和变形破坏特征,其破坏机理一直是学术界和工程领域关注的难点和重点.以往的研究通常从宏观角度去研究和探讨混凝土的破坏机理,将混凝土视为均质材料.这种简化在某种程度上可以满足当前大多数工程的需要,但不能准确描述混凝土非均质特性,难以揭示混凝土变形和破坏的物理机制.
数字图像处理(digital image processing,DIP)是一种利用计算机技术将图像转换成数字形式的方法,并且应用各种数学算法从图像中提取重要信息.为了准确描述混凝土的复杂微观特征,通过使用DIP技术,运用数学算法对原始非均质混凝土图像进行数字处理,能够较好地提取所需要的重要信息参数,为混凝土内部非均质特征分析提供依据.在此基础上,用近场动力学方法进行建模,可以从细观角度描述混凝土的破坏特点.本文采用DIP技术对混凝土微观结构特征进行提取,并基于近场动力学理论和方法,建立混凝土微观结构模型,对该模型进行了受力分析.研究结果拓展了近场动力学方法的应用领域,为后续研究奠定了基础.
1 相关工作国内外研究者已经进行了许多有关DIP技术在混凝土力学性能方面的研究工作[1].文献[2]运用Laplacian、Canny等算法对图像进行二值化边缘检测.文献[3]依次采用聚变类算法、插值图像法及阈值分割法等7种算法用于提取混凝土细观结构,为后期模拟混凝土损伤过程提供较为真实的细观结构参数,通过Matlab图像处理工具对图像进行形态学处理和边缘检测,利用几何矢量转换技术获取混凝土细观结构图,建立细观数值模型,并通过模型进行混凝土力学性能的有限元分析.文献[4-5]提出一种改进的动态Metropolis方法,能够有效地分割CT扫描图,并能进一步分析混凝土内部缺陷在破坏过程中的动态分布.文献[6]提出细观结构探测及宏观建模的关键技术问题,并进行了探讨.文献[7]基于DIP技术对混凝土CT扫描图片进行三维几何重构,较好地模拟了混凝土的单轴受力过程.
对混凝土渐近破坏全过程的模拟一直受到研究者的关注,但在微观缺陷的发展、三维裂纹的扩展、裂纹间的相互作用等方面存在计算精度和效率不高的问题.以经典连续介质理论为基础的传统方法在模拟裂纹扩展时面临瓶颈,根本原因在于裂纹引起的不连续,这一“不连续”现象的准确描述随着新兴的近场动力学思想[8]的提出有望得以解决.近场动力学思想将分子动力学和无网格法的优势相结合,不同于传统的局部模型的偏微分方程求解,而是基于非局部思想,采用直接积分的形式,不考虑位移场的连续与否,在一定近场范围内通过积分来计算具有一定影响域的材料的点之间的相互作用力[9].
近场动力学可视为一种宏观尺度的分子动力学方法,该方法采用统一的模型和求解体系描述从原子尺度到宏观尺度的力学行为,突破了经典分子动力学模型在求解尺度上的局限,也避免了传统的多尺度模型在不同尺度力学量传递等方面的复杂性.国内外已有的基于近场动力学方法对混凝土进行研究的成果中,大都将混凝土视为均匀材料,未考虑其微观特征对其性能的影响[10-15].本文采用DIP技术对混凝土微观结构特征进行提取,并基于近场动力学理论和方法建立了混凝土微观结构模型.
2 混凝土DIP和物质点坐标假设混凝土的内部结构是由骨料、砂浆以及两者之间的过渡界面构成的.图 1为试验中使用的边长为150 mm的混凝土标准试块截面,该试块骨料采用连续级配且随机投放,其制备过程和养护过程都较为理想.切割混凝土试件后,拍照得到混凝土截面图.根据像素质量和大小,选择像素尺寸400×400,在处理过程中将主要考虑骨料和砂浆,所得的结果均为像素面积,需要经过比例转换才能得到真实结果.以该算例为例,混凝土截面图在经过图像处理后,截面尺寸由150 mm×150 mm转化为像素尺寸400×400,在经过比例转化后,就可以得到混凝土的真实骨料参数,其截面二值图如图 2所示.

|
图 1 混凝土试块截面 Figure 1 Concrete cross section |

|
图 2 混凝土截面二值图 Figure 2 Binary image of concrete cross section |
DIP技术将连续型图像变为离散型图像,从而将混凝土截面图处理转化为像素点图像的计算.在非均质混凝土二值图的计算中,灰度值为0的像素点代表砂浆,灰度值为1的像素点代表骨料.灰度值为0、1的像素点所在的位置,可以认为是混凝土中材料的对应坐标点,表示为
| $ \left\{ \begin{array}{l} {x_i} = \frac{{\left( {{n_i} - 1} \right) \times 0.150}}{{N - 1}}, \\ {y_i} = \frac{{\left( {{m_i} - 1} \right) \times 0.150}}{{M - 1}}, \end{array} \right. $ | (1) |
式中:ni、mi为灰度值为0、1时像素点对应的行列位置;N、M为混凝土二值图的像素尺寸.
通过(1)式可以计算出混凝土各个内部材料的物质点坐标,从而在混凝土图像处理中,计算出其内部砂浆、骨料、孔隙等的物质点坐标,为分析混凝土破坏过程提供依据.
3 近场动力学理论及建模方法近场动力学理论假定在计算域内的任意无穷小粒子都满足牛顿第二定律,不需要假设物质为连续体,也不用考虑“应力”和“应变”的关系.从近场动力学方法的基本方程可以看出,该模型是典型的考虑物质点之间的相互作用并基于空间积分方程来求解的,因而可以有效地对基于偏微分方程求解的传统连续介质力学模型和传统非局部模型进行补充.
近场动力学假定在某一空间域R内,在某一时刻t,R内的任一物质点x,与它周围一定空间范围δ内的所有物质点,均存在相互作用力,其运动方程为
| $ \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \int_R {f\left( {u\left( {x', t} \right), u\left( {x, t} \right), x', x, t} \right){\rm{d}}{V_{x'}} + b\left( {x, t} \right), } \forall x \in R, t \ge 0, $ | (2) |
式中:ρ为物质点的密度;u为物质点的位移;f为物质点x与x'之间的相互作用力函数,即本构力函数;x'∈R,‖x'-x‖≤δ,δ为近场范围尺寸;b为单位体积物质所受的外载荷,即外载荷密度.
进一步积分得
| $ {L_u}\left( {x, t} \right) = \int_R {f\left( {u\left( {x', t} \right), u\left( {x, t} \right), x' - x} \right){\rm{d}}{V_{x'}}} , \forall x \in R, t \ge 0. $ | (3) |
故在空间域R上,近场动力学方法的运动方程为
| $ \rho \ddot u = {L_u} + b, t \ge 0. $ | (4) |
由式(2)~(4),可得近场动力学方法的基本方程为
| $ \rho \left( x \right)\ddot u\left( {x, t} \right) = \int_H {f\left( {x, x', u\left( {x, t} \right), u\left( {x', t} \right), t} \right){\rm{d}}{V_{x'}}} + b\left( {x, t} \right), \forall x \in R, t \ge 0, $ | (5) |
式中:H为空间域内物质点x的近场范围,即以x为中心,半径为δ的球域,H=H(x, δ):={x'∈R:‖x'-x‖≤δ}.
近场动力学方法采用空间积分方程来描述物质点的运动,消除了不连续性带来的求解困难,在求解不连续问题时具有明显的优势.为了描述材料的破坏特征,近场动力学模型中引入了伸长率的概念[9],其表达式为
| $ s\left( {\eta , \xi } \right) = \frac{{\left| {\eta + \xi } \right| - \left| \xi \right|}}{{\left| \xi \right|}}. $ | (6) |
临界伸长率s0是材料的固有属性,当物质点对的伸长量超越了临界伸长率时,其间生成的“键”将发生不可逆的断裂,此时认为该物质点对间不再发生相互作用,该点对发生破坏.近场动力学以s0定义其破坏准则,并引入一个布尔函数μ(ξ, t)来描述物质点对间“键”的破坏情况,可以表示为
| $ \mu \left( {\xi , t} \right) = \left\{ {\begin{array}{*{20}{l}} {1, }&{s\left( {t', \xi } \right) < {s_0}, 0 < t' < t, }\\ {0, }&{{\rm{其他}}{\rm{.}}} \end{array}} \right. $ | (7) |
在此基础上,将t时刻材料的损伤[9]定义为
| $ \varphi \left( {x, t} \right) = 1 - \frac{{\int_{{H_x}} {\mu \left( {t, \xi } \right){\rm{d}}{V_{x'}}} }}{{\int_{{H_x}} {{\rm{d}}{V_{x'}}} }} $ | (8) |
由式(6)~(8)可见,近场动力学模型中对材料损伤的描述包含于本构力函数中,在分析破坏问题时,不需要进行裂纹位置及路径的预判,也无须使用临界应力强度因子等断裂准则.在近场动力学模型中,材料的“不连续”是方程解的一部分,裂纹将自然出现和扩展,直至破坏.本构力函数包含了材料的物性信息,均匀各向同性微观线弹性材料的本构力函数[9]为
| $ f = f\left( {\eta , \xi } \right) = \frac{{\xi + \eta }}{{\left| {\xi + \eta } \right|}}sc\left( {\xi , \delta } \right), $ | (9) |
式中:c(ξ, δ)表征物质点对的刚度,称为微观弹性模量函数,c(ξ, δ)=c(0, δ)g(ξ, δ),c(0, δ)称为集中函数,用来描述两物质点在无限靠近时的点对刚度;g(ξ, δ)称为本构力核函数,反映了物质点间长程力的强度随两物质点间距离的变化规律.
采用改进的二次多项式型本构力核函数[16],其表达式为
| $ g\left( {\xi , \delta } \right) = \left\{ {\begin{array}{*{20}{l}} {1 - {{\left( {\frac{\xi }{\delta }} \right)}^2}, }&{\xi \le \delta , }\\ {0, }&{\xi > \delta .} \end{array}} \right. $ | (10) |
该函数充分考虑了近场范围尺寸δ对本构力函数f的影响,其计算精度也有所提高.
4 数值算例将提取出来的骨料参数坐标导入ABAQUS中,将混凝土视为由骨料和砂浆构成的二相材料,建立的混凝土非均质几何模型如图 3所示.其中骨料的弹性模量为80 GPa,泊松比为0.28,密度为2 600 kg/m3;砂浆的弹性模量为28.6 GPa,泊松比为0.16,密度为2 200 kg/m3.

|
图 3 混凝土非均质几何模型 Figure 3 Inhomogeneous geometric model of concrete |
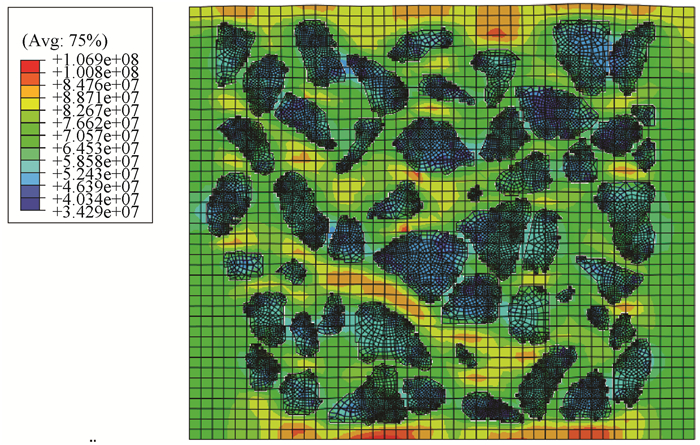
对所构建的计算模型进行Y方向的轴向压缩模拟,构造简单的正方形晶格,晶格常数Δx=0.001 m,近场范围δ取3倍的晶格常数.模型中共包含203 401个物质点,其中骨料点51 385个,砂浆点152 016个,时间步长Δt设置为1×10-7 s.加载方式采用位移加载,分别取上下边界的三排粒子进行加载,位移加载总量为1 mm.损伤云图模拟结果如图 4所示.可以看出,混凝土的破坏是先从砂浆开始,然后再向骨料发展,这与混凝土的实际破坏形式相符.因此,通过DIP技术可以将混凝土的内部特征真实地反映出来,并建立相应的力学模型.DIP技术适用于多种分析软件,本文采用ABAQUS软件进行建模,均可以得到正确的结果,表明所采用的研究方法具有通用性.此外,模拟结果和有限元结果吻合较好,表明在无损变形下,基于近场动力学方法的结果是准确可靠的.
|
图 4 损伤云图模拟 Figure 4 Damage image simulation |
采用DIP技术对混凝土微观结构特征进行提取,在此基础上,基于近场动力学理论和方法,建立混凝土微观结构模型,并进行了受力分析.研究结果表明,DIP技术极大优化了对混凝土内部微观结构的提取,方便建立混凝土几何模型,为研究混凝土的破坏过程与破坏机理提供了技术支持.采用改进的二次多项式型本构力核函数,提高了计算结果的准确性.本文的研究手段和方法也为混凝土非均质特性的研究提供了新的思路.今后需要进一步研究传统的应力张量、应变张量在近场动力学方法中的描述,以及骨料与水泥砂浆之间过渡面的参数提取,从而对非均质特性展开更加深入细致的研究.
| [1] |
YUE Z Q, CHEN S, THAM L G, et al. Finite element modeling of geomaterials using digital image processing[J]. Computers and geotechnics, 2003, 30(5): 375-397. DOI:10.1016/S0266-352X(03)00015-6 (  0) 0) |
| [2] |
姜袁, 柏巍, 彭刚. 基于CT图像的混凝土细观结构边缘检测技术[J]. 武汉大学学报(工学版), 2008, 41(1): 77-80. (  0) 0) |
| [3] |
郝景宏, 姜袁, 梅世强, 等. 基于CT图像处理技术的混凝土损伤演化研究[J]. 人民长江, 2010, 41(17): 79-83. DOI:10.3969/j.issn.1001-4179.2010.17.021 (  0) 0) |
| [4] |
赵亮, 李昌华, 党发宁, 等. 基于CT图像的建筑混凝土破裂细观结构智能处理分析[J]. 西安建筑科技大学学报(自然科学版), 2010, 42(5): 751-756. DOI:10.3969/j.issn.1006-7930.2010.05.026 (  0) 0) |
| [5] |
赵亮, 李昌华, 党发宁, 等. X射线混凝土CT图像处理方法分析研究[J]. 武汉理工大学学报, 2011, 33(3): 98-102. DOI:10.3963/j.issn.1671-4431.2011.03.021 (  0) 0) |
| [6] |
王梦蔚, 卢广达, 黄丹. 基于CT扫描试验及数字图像处理的混凝土宏细观建模研究[J]. 混凝土, 2014(11): 27-30. DOI:10.3969/j.issn.1002-3550.2014.11.007 (  0) 0) |
| [7] |
杨进波, 阎培渝. 混凝土边界效应层中粗骨料的分布特征[J]. 建筑材料学报, 2009, 12(5): 580-583. DOI:10.3969/j.issn.1007-9629.2009.05.016 (  0) 0) |
| [8] |
黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448-459. (  0) 0) |
| [9] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the mechanics and physics of solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 (  0) 0) |
| [10] |
HUANG D, ZHANG Q, QIAO P Z, et al. Damage and progressive failure of concrete structures using non-local peridynamic modeling[J]. Science China technological sciences, 2011, 54(3): 591-596. DOI:10.1007/s11431-011-4306-3 (  0) 0) |
| [11] |
沈峰, 章青, 黄丹, 等. 冲击荷载作用下混凝土结构破坏过程的近场动力学模拟[J]. 工程力学, 2012, 29(s1): 12-15. (  0) 0) |
| [12] |
SHEN F, ZHANG Q, HUANG D. Damage and failure process of concrete structure under uniaxial compression based on peridynamics modeling[J]. Mathematical problems in engineering, 2013(1): 206-232. (  0) 0) |
| [13] |
沈峰, 章青, 黄丹, 等. 基于近场动力学理论的混凝土轴拉破坏过程模拟[J]. 计算力学学报, 2013, 30(s1): 79-83. (  0) 0) |
| [14] |
GERSTLE W, SAU N, SILLING S. Peridynamic modeling of concrete structures[J]. Nuclear engineering and design, 2007, 237(12): 1250-1258. (  0) 0) |
| [15] |
GERSTLE W, SAU N, SILLING S. Peridynamic modeling of plain and reinforced concrete structures[C]//Proceedings of 18th International Conference on Structural Mechanics in Reactor Technology.Beijing, 2005: 1-10. http://cpfd.cnki.com.cn/article/cpfdtotal-egvd200508001016.htm
(  0) 0) |
| [16] |
沈峰, 章青, 黄丹, 等. 基于近场动力学方法的结构准静态变形的定量计算[J]. 重庆大学学报, 2016, 39(5): 49-55. (  0) 0) |
 2018, Vol. 50
2018, Vol. 50

