全息技术因能同时记录光场的振幅和相位信息而备受关注,是真正意义上的空间三维成像技术.传统全息技术采用光学记录和光学再现的方式获取物光场信息,对照明光源的相干性和实验条件要求较高,使其始终无法走出实验室.随着高分辨率CCD、COMS等图像传感器的发展,非相干数字全息技术得到了快速发展.非相干数字全息是在非相干光源照明下,用CCD或CMOS代替干板记录全息图,通过数值计算方法重建物光场的一种成像技术.其记录原理为:非相干光源照明下的三维物体表面可以看作无穷多个空间非相干点源的集合,每一个点发出的球面光波经某种分光技术[1]分成两束自相干光,这两束光相互干涉形成点源全息图(点扩散函数),物体表面所有点的点源全息图非相干叠加后被CCD记录形成全息图.基于空间光调制器(SLM)分光的单通道非相干数字全息(又称菲涅耳非相干相关全息,FINCH)是由Rosen等[2-3]于2007年首次提出的,系统的核心是由SLM和CCD组成的非相干干涉仪,SLM兼具分束器和移相器的作用.目前FINCH技术已被成功应用于白光反射全息成像[2, 4-5]、三维荧光物体的多色全息成像[3]、三维显微成像和基于菲涅耳元件的合成孔径系统等[6-10].
20世纪80年代出现的光谱成像技术[11-14]能同时获得样品的二维平面信息和光谱信息,在遥感探测、军事防伪、农业病虫害监测等方面得到了很好的应用.为保证时间相干性, 非相干数字全息系统中通常需要引入窄带滤光片,因此非相干数字全息系统严格而言是准单色系统,无法获得物体的光谱信息;而光谱成像技术只能获得物体的二维平面信息,在获取物体的三维空间信息方面无能为力.本文结合非相干数字全息和光谱成像技术的特点,首次提出非相干数字全息技术与光谱成像技术相结合,实现基于非相干数字全息的光谱成像系统,在FINCH系统中引入液晶可调滤波器,通过编程控制可调滤波器输出不同中心波长的窄带光,记录三维物体在不同波长下的全息图.从波动光学的角度分析系统的点扩散函数,给出系统的横向放大率和再现距离表达式,采用该系统对分辨率成像进行了验证.非相干数字全息光谱成像系统的最大优点是能同时获得物体的三维空间信息和光谱信息,成像速度快,无需时间和空间上的扫描,在军事探测、艺术品鉴赏、材料分析和刑事侦查等方面具有潜在的应用价值.
1 FINCH多光谱成像图 1为典型FINCH成像系统示意图,假设透镜(焦距f0)焦平面外任一点源(xs, ys, -zs),经菲涅尔衍射后,在透镜前表面的复振幅分布为
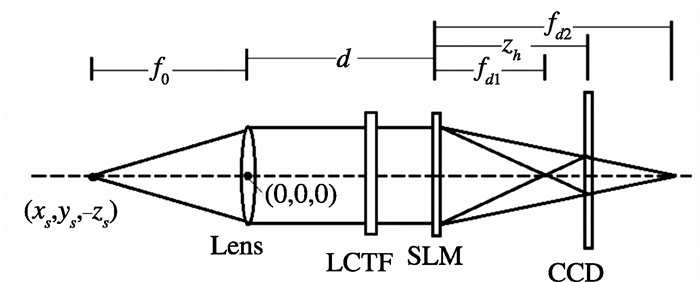
|
图 1 典型FINCH成像系统示意图 Figure 1 Schematic diagram of FINCH imaging system |
| $ C\left( {{r_s}, {z_s}} \right)L\left( {\frac{{-r}}{{{z_s}}}} \right)Q\left( {\frac{1}{{{z_s}}}} \right). $ |
定义L(rs)=exp[i2πλ-1(xsx+ysy)],xs和ys分别为rs在x轴和y轴方向的分量,Q(b)=exp[iπbλ-1(x2+y2)], C(rs, zs)=exp[iπ(zsλ)-1(xs2+ys2)]为仅与点源位置有关的复常数.经透镜和距离d后到达SLM前表面的复振幅分布为
| $ C\left( {{r_s}, {z_s}} \right)L\left( {\frac{{-r}}{{{z_s}}}} \right)Q\left( {\frac{1}{{{z_s}}}} \right)Q\left( {-\frac{1}{{{f_0}}}} \right)*Q\left( {\frac{1}{d}} \right), $ |
式中:“*”代表卷积运算.
液晶SLM可选择透射式也可选择反射式,一般反射式SLM为硅基液晶空间光调制器(LCOS-SLM),具有更高的开口率和光能利用率.
假设在SLM上加载两个透镜(掩模波长为λ0)焦距分别为fd1和fd2的相位掩模,则记录波长为λ时,其振幅反射/透射系数为
| $ B\exp \left( {{\rm{i}}\theta } \right)Q\left( {\frac{{-\lambda }}{{{\lambda _0}{f_{d1}}}}} \right) + B'Q\left( {\frac{{-\lambda }}{{\lambda {_0}{f_{d2}}}}} \right), $ |
式中:θ为相位常数(两球面波的相位差).
经SLM反射/透射再经距离zh后到达CCD表面,CCD表面的强度分布(即系统点扩散函数)为
| $ {I_p}\left( {x, y;{r_s}, {z_s};\lambda } \right) = {B^2} + {B'^2} +\\ BB'\exp \frac{{{\rm{i \mathsf{ π} }}}}{{\lambda \cdot {z_r}}}\left\{ {{{\left[{x + \frac{{{f_e} \cdot {z_h}}}{{{z_s}\left( {{f_e} + d} \right)}} \cdot {x_s}} \right]}^2} + {{\left[{y + \frac{{{f_e} \cdot {z_h}}}{{{z_s}\left( {{f_e} + d} \right)}} \cdot {y_s}} \right]}^2}} \right\} \cdot {{\rm{e}}^{{\rm{i}}\theta }} + c. + c., $ | (1) |
式中:
为满足两球面波在CCD表面上最优干涉,zh的取值应满足:
| $ {z_h} = \frac{{2{f_{d1}}{f_{d2}}}}{{{f_{d1}} + {f_{d2}}}} \cdot \frac{{{\lambda _0}}}{\lambda }. $ |
系统的横向放大率为
| $ {M_T}\left( {{z_s}, \lambda } \right) = \frac{{-{f_e}{z_h}}}{{{z_s}\left( {{f_d} + d} \right)}}. $ |
若三维物体表面的反射强度分布为g(xs, ys, zs),则CCD上记录的干涉图案为三维物体表面所有点源全息图的非相干叠加,即
| $ H\left( {x, y, \lambda } \right) = \iiint {g\left( {{x_s}, {y_s}, {z_s}} \right){I_p}\left( {x, y;{r_s}, {z_s};\lambda } \right){\rm{d}}{x_s}{\rm{d}}{y_s}{\rm{d}}{z_s}.} $ | (2) |
利用同轴数字全息三步相移法,CCD记录3张具有不同相位因子的全息图,在计算机中进行线性叠加, 得到三维物体最终的复值全息HF(x, y, λ), 最后进行菲涅尔逆向传输计算来获得物体的再现像,即
| $ S\left( {x', y', {z_r}, \lambda } \right) = \iint {{H_F}\left( {x, y, \lambda } \right)\exp \left\{ {\frac{{{\rm{i \mathsf{ π} }}}}{{\lambda {z_r}}}\left[{{{\left( {x'-x} \right)}^2} + {{\left( {y'-y} \right)}^2}} \right]} \right\}{\rm{d}}x{\rm{d}}y.} $ | (3) |
通过计算机控制可调滤波器(LCTF)输出光的中心波长λ,即可得到不同波长的再现像.FINCH系统单通道成像是FINCH多光谱成像的一个特例,此时记录波长λ等于SLM加载透镜的掩模波长λ0.
2 实验部分 2.1 分辨率板单通道成像实验图 2为FINCH成像系统实验光路示意图.被测物体为USAF 1951分辨率板,放在准直透镜L1(焦距250 mm)前252 mm处.准直透镜L1到SLM(Holoeye Pluto,像素为1 920×1 080,像素尺寸为8 μm)的距离为115 mm,SLM到记录元件CCD(像素为1 344×1 024,像素尺寸为6.45 μm)的距离为250 mm.为实现分光作用,在SLM上加载焦距分别为fd1=245 mm、fd2=255 mm的双透镜掩模.LCTF为可调滤波器,设定中心波长为632.8 nm,带宽为20 nm.BS1、BS2为分束器,偏振片的偏振轴平行于SLM的液晶长轴方向.
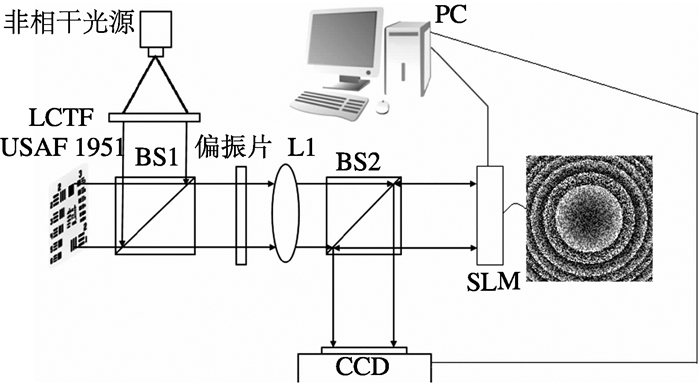
|
图 2 FINCH成像系统实验光路示意图 Figure 2 Experimental set-up of FINCH imaging system |
图 3为分辨率板FINCH系统全息再现结果,图 3(a)为常相位因子θ1=0°的全息图,最终数值重建得到的最佳焦平面的再现像如图 3(b)所示. 图 3(b)的实验结果表明,FINCH技术能够快速记录三维物体的全息图,无需对物体在空间或时间上进行扫描.

|
图 3 分辨率板FINCH系统全息再现结果 Figure 3 The hologram reconstruction of FINCH system |
为完成FINCH系统与光谱成像技术的结合实验,需要通过计算机控制可调滤波器(LCTF)输出具有不同中心波长的窄带光.LCTF输出光的中心波长分别为480、520、560、600、640、680、720 nm,带宽均为20 nm.用CCD分别记录各波长下分辨率板的不同常相位因子的3张全息图,最终最佳焦平面处的数值再现像如图 4所示.

|
图 4 中心波长分别为480、520、560、600、640、680、720 nm时的再现像 Figure 4 The reconstruction images with center wavelengths of 480, 520, 560, 600, 640, 680, 720 nm respectively |
从图 4可以看出,各再现像的放大率会随记录波长λ的增大而减小,其原因是系统的横向放大率是波长λ的函数,当改变中心波长时,与之对应的再现像的横向放大率也会随之改变.
为说明图 4中各再现像的质量差异,选用数字图像处理中的方差评价方法.图像的方差反映了图像整体灰度层次的丰富程度,方差越大说明图像的灰度层次越多,对比度越高,图像包含的信息就越多.其计算公式可以表示为
| $ {\sigma ^2} = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {p\left( {i, j} \right)-\mu } \right)}^2}} } }}{{MN}}, $ |
式中:M、N分别代表图像的行数、列数;p(i, j)表示在第i行、第j列元素的灰度值;μ是图像的均值.
利用方差公式计算图 4中各再现像的方差值, 方差示意图如图 5所示.可以看出,640 nm处再现像的方差值最大,即再现像的对比度最高;其他波长处再现像的方差值降低,即再现像的对比度均低于640 nm处的再现像.主要原因为:一方面,由图 6所示的光源光谱曲线可以看出,不同波长能量分布不均匀,若光波能量较低,则背景噪音会相应增加,干涉条纹的对比度会降低,从而降低了再现像的对比度.另一方面,SLM作为衍射光学元件,使全息成像过程受到了严重的色差影响;因SLM校准的波长是632.8 nm,所以其他波长处的再现像会因对校准波长的不同偏离程度而出现再现像质量降低的现象.
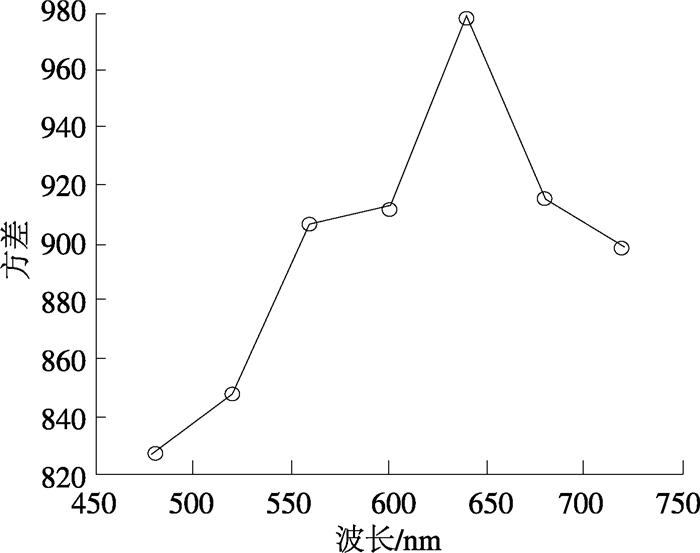
|
图 5 图 4中各再现像的方差示意图 Figure 5 The variance schematic diagram of the reconstruction images shown in Fig. 4 |
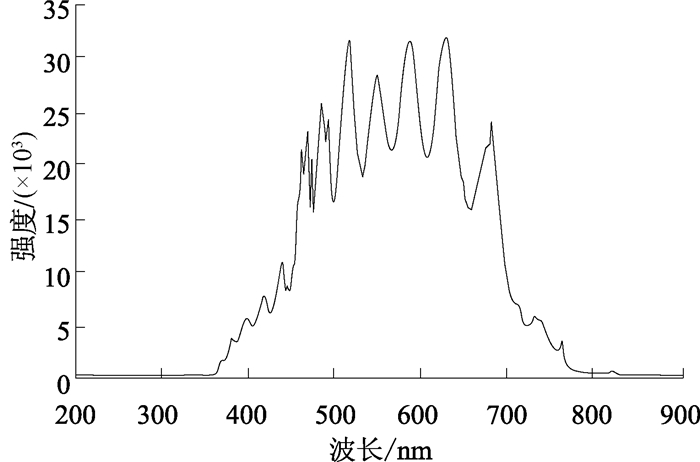
|
图 6 光源光谱曲线 Figure 6 Spectrum curve of the light source |
结合菲涅耳非相干相关数字全息技术和光谱成像技术的优点,提出能够同时获得物体三维空间信息和光谱信息的四维成像系统,即在菲涅耳非相干相关数字全息系统中引入空间滤波器.利用菲涅耳衍射理论推导了菲涅耳非相干相关数字全息技术用于多光谱成像时的点扩散函数,并给出了横向放大率、再现距离与记录波长之间的关系,用分辨率板单通道成像实验和分辨率板多光谱成像实验进行了验证.针对多光谱成像实验中各再现像质量之间的差异进行了像质评价,得出640 nm处再现像的对比度最高,并对其产生原因进行了分析.
| [1] |
万玉红, 满天龙, 陶世荃. 非相干全息术成像特性及研究进展[J]. 中国激光, 2014, 41(2): 0209004. (  0) 0) |
| [2] |
ROSEN J, BROOKER G. Digital spatially incoherent Fresnel holography[J]. Optics letters, 2007, 32(8): 912-914. DOI:10.1364/OL.32.000912 (  0) 0) |
| [3] |
ROSEN J, BROOKER G. Fluorescence incoherent color holography[J]. Optics express, 2007, 15(5): 2244-2250. DOI:10.1364/OE.15.002244 (  0) 0) |
| [4] |
刘英臣, 范金坪, 曾凡创, 等. 白光菲涅耳非相干数字全息的纪录、再现及实现[J]. 中国激光, 2013, 40(10): 1009002. (  0) 0) |
| [5] |
MAN T L, WAN Y H, CHEN H, et al.Quantitative evaluation of spatial phase light modulator characteristics in Fresnel incoherent correlation holography[C]//The International Society for Optical Engineering. Beijing, 2012:13-19. https://www.spiedigitallibrary.org/journals/Journal-of-MicroNanolithography-MEMS-and-MOEMS/volume-14/issue-04/041307/Incoherent-digital-holography-with-phase-only-spatial-light-modulators/10.1117/1.JMM.14.4.041307.full
(  0) 0) |
| [6] |
ROSEN J, BROOKER G. Non-scanning motionless fluorescence three-dimensional holographic microscopy[J]. Nature photonics, 2008, 2(3): 190-195. DOI:10.1038/nphoton.2007.300 (  0) 0) |
| [7] |
BOUCHAL P, BOUCHAL Z. Wide-field common-path incoherent correlation microscopy with a perfect overlapping of interfering beams[J]. Journal of the European optical society, 2013, 8(1): 92-103. (  0) 0) |
| [8] |
KATZ B, ROSEN J. Could SAFE concept be applied for designing a new synthetic aperture telescope?[J]. Optics express, 2011, 19(6): 4924-4936. DOI:10.1364/OE.19.004924 (  0) 0) |
| [9] |
ROSEN J, SIEGEL N, BROOKER G. Theoretical and experimental demonstration of resolution beyond the Rayleigh limit by FINCH fluorescence microscopic imaging[J]. Optics express, 2011, 19(27): 26249-26268. DOI:10.1364/OE.19.026249 (  0) 0) |
| [10] |
SIEGEL N, ROSEN J, BROOKER G. Reconstruction of objects above and below the objective focal plane with dimensional fidelity by FINCH fluorescence microscopy[J]. Optics express, 2012, 20(18): 19822-19835. DOI:10.1364/OE.20.019822 (  0) 0) |
| [11] |
GOETZ A F, VANE G, SOLOMON J E, et al. Imaging spectrometry for earth remote sensing[J]. Science, 1985, 228(4704): 1147-1153. DOI:10.1126/science.228.4704.1147 (  0) 0) |
| [12] |
BOARDMAN J W. Inversion of imaging spectrometry data using singular value decomposition[C]//Proceedings of 12th Canadian Symposium on Remote Sensing. Vancouver, 1989:2069-2072.
(  0) 0) |
| [13] |
CLARK R N, KING T V V, KLEJWA M, et al. High spectral resolution reflectance spectroscopy of minerals[J]. Journal of geophysical research, 1990, 95(8): 12653-12680. (  0) 0) |
| [14] |
CURRAN P J. Imaging spectrometry[J]. Progress in physical geography, 1994, 18(2): 247-266. DOI:10.1177/030913339401800204 (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


