信息隐藏(data hiding,DH)是一种将秘密信息嵌入到载体中,并且能够实现版权保护、身份认证、隐私保护等需求功能的安全技术[1-2].可逆信息隐藏算法作为信息隐藏的一个重要分支,在准确提取出嵌入信息的基础上还可以对载体实现可逆恢复,在军事作战地图、远程医疗和司法取证等特殊领域中发挥着重要作用[3-5].
近年来,一些基于预测误差扩展(prediction-error expansion, PEE)的可逆信息隐藏方法由于视觉效果好而受到关注[6-8].由于该类方法只对特定PEE进行秘密信息嵌入,并且像素值变化的最大幅度为1.因此,这类方法以牺牲嵌入容量为代价获得了较好的视觉效果.文献[9]在传统PEE基础上提出一种嵌入性能更佳的像素值排序(pixel value ordering,PVO)方法.在PVO方法中,首先对块内像素值进行排序,然后利用次大/次小值对最大/最小值进行预测,从而对最值扩展实现信息嵌入.此外,文献[9]还提出了利用次大和次小像素值之间的差值来定义像素块复杂度,根据得到的复杂度优先在平滑的像素块中嵌入秘密数据.在文献[9]基础上,文献[10]提出一种PVO-K嵌入方法,其中K是最大/最小像素值的个数,在信息嵌入过程中,所有最大/最小像素值整合为一个整体用来嵌入信息,该方法还提出了一种从邻近像素点计算出块复杂度的策略.文献[11]则设计了一种新的预测误差方法,将预测误差0引入到嵌入过程中,同样取得了比传统PVO方法更好的效果.这三种PVO方法[9-11]存在的主要问题是:为了在一个较大的像素块内追求高峰值信噪比,只能得到相对较小的嵌入容量.鉴于此,文献[12]提出动态像素块分类方法,该方法在纹理复杂的区域选择较大的像素块来保证高峰值信噪比,而在光滑区域选择一个较小的像素块来保证高嵌入容量.根据像素块复杂度将根块(根块为未划分的原始像素块)划分为复杂、正常和平滑三类.然而在动态分块策略中,4*4复杂根像素块作为信息载体具有一定冗余,但该策略对其不做任何操作,导致存在的可嵌位置无法得到充分利用.针对这个问题,本文设计了一种通用的序列动态选择可逆信息隐藏算法.通过对大量复杂像素块的分析,发现个别像素值突变导致复杂度较大,但其本身序列仍具有可嵌的冗余空间.在不破坏根像素块复杂度的前提下,利用定义的阈值从复杂块中动态选择可嵌入的平滑像素序列,最后对该序列最值进行I-PVO操作[11],实现信息的可逆嵌入.
1 相关知识 1.1 I-PVO算法PVO类算法通过有效利用块内像素间的相似性,从而在低失真条件下获得足够的嵌入容量.文献[11]在文献[9]基础上,在嵌入过程中主要对预测误差0加以利用,从而优化了PVO类可逆信息隐藏算法的性能.
为对像素块内最大值进行预测修改,将图像分割成一系列非重叠的像素块,有以下定义.
定义1 像素块内升序排列{xσ(1),xσ(2),…,xσ(n)},由对每个像素块内n个像素点{x1,x2,…,xn}排序得到.如果i < j,那么xσ(i)≤xσ(j).
定义2[9] 预测误差PE为
| $ PE = {x_{\sigma \left( n \right)}} - {x_{\sigma \left( {n - 1} \right)}}. $ | (1) |
定义3[11] 预测误差d为
| $ d = \left\{ {\begin{array}{*{20}{l}} {{x_{\sigma (n)}} - {x_{\sigma (n - 1)}},}&{{\text{if }}\sigma (n) \ge \sigma (n - 1),}\\ {{x_{\sigma (n - 1)}} - {x_{\sigma (n)}},}&{{\text{otherwise}}.} \end{array}} \right. $ | (2) |
在定义3下,d将会出现非正的情况,并且误差直方图中峰值点将在0处(而文献[9]中峰值点在1处).预测误差PE与d具有以下相关性:
| $ \left\{ {\begin{array}{*{20}{l}} {PE(0) = d(0),}\\ {PE(k) = d(k) + d( - k).} \end{array}} \right. $ | (3) |
在文献[9]中,只有PE(1)用于扩展,而在文献[11]中,在d(0)和d(1)处都用于扩展.由于d(0)+d(1)-PE(1)=d(0)-d(-1)>0,因此通过该优化可以实现嵌入容量的提高.
定义4 嵌入信息b,以二进制0、1的方式表示,通过修改预测误差d实现信息嵌入.
| $ {d^\prime } = \left\{ {\begin{array}{*{20}{l}} {d + b,}&{{\text{if }}d = 1,}\\ {d + 1,}&{{\text{if }}d > 1,}\\ {d - b,}&{{\text{if }}d = 0,}\\ {d - 1,}&{{\text{otherwise}}{\text{.}}} \end{array}} \right. $ | (4) |
嵌入后的像素值x′σ(n)为
| $ x_{\sigma (n)}^\prime = {x_{\sigma (n - 1)}} + \left| {{d^\prime }} \right| = \left\{ {\begin{array}{*{20}{l}} {{x_{\sigma (n)}} + b,}&{{\text{if }}d = 1,}\\ {{x_{\sigma (n)}} + 1,}&{{\text{if }}d > 1,}\\ {{x_{\sigma (n)}} + b,}&{{\text{if }}d = 0,}\\ {{x_{\sigma (n)}} + 1,}&{{\text{otherwise}}{\text{.}}} \end{array}} \right. $ | (5) |
同样,由于最大值在嵌入信息处理后非减,而其他像素点的数值不变,因此可以保证像素值的顺序不变.提取端预测误差d′可以利用同样的方法获得,并且利用式(6)对嵌入数据进行提取.
| $ b = \left\{ {\begin{array}{*{20}{l}} {{d^\prime } - 1,}&{{\text{if }}{d^\prime } = 1{\text{ or }}{d^\prime } = 2,}\\ { - {d^\prime },}&{{\text{if }}{d^\prime } = 0{\text{ or }}{d^\prime } = - 1.} \end{array}} \right. $ | (6) |
原始数据经过信息提取后,利用式(7)实现可逆恢复.
| $ {x_{\sigma (n)}} = \left\{ {\begin{array}{*{20}{l}} {x_{\sigma (n)}^\prime - b,}&{{\text{if }}{d^\prime } = 1{\text{ or }}{d^\prime } = 2,}\\ {x_{\sigma (n)}^\prime - 1,}&{{\text{if }}{d^\prime } > 2,}\\ {x_{\sigma (n)}^\prime - b,}&{{\text{if }}{d^\prime } = 0{\text{ or }}{d^\prime } = - 1,}\\ {x_{\sigma (n)}^\prime - 1,}&{{\text{otherwise}}{\text{.}}} \end{array}} \right. $ | (7) |
基于像素块内最小值的嵌入方法和基于像素块内最大值的嵌入方法类似,同样通过引入预测误差峰值0来提升嵌入容量.
1.2 动态分块文献[12]在文献[11]基础上进一步优化,提出一种将两个不同尺寸像素块结合使用的动态像素块分割方法.为确保在信息嵌入之后原来的复杂性得以保留,该方法重新对块复杂度进行了定义.
定义5 如果原始图像被分割为一系列大小为4*4且互不重叠的像素块,这种分割方法得到根像素块,表示为Br.如果将根像素块分割为一系列大小为2*2的子块,这种分割方法得到叶像素块,表示为Bl.
定义6 根块的复杂度NL为
| $ N L=\max \left(s l\left(B_{l}^{1}\right), s l\left(B_{l}^{2}\right), \cdots\right)-\min \left(\operatorname{sm}\left(B_{l}^{1}\right), s m\left(B_{l}^{2}\right), \cdots\right), $ | (8) |
其中:sl(·)和sm(·)分别表示指定块的次大和次小像素值的选择函数.信息无论是嵌入在根块中还是子块中,经排序后像素sl(Bli)、sm(Bli)(1≤i≤4)的数值始终不发生变化.然后将根块通过复杂度阈值T1和T2进行分类:当NL>T1时为Ⅰ型像素块,该块归类为不用于数据嵌入的复杂块;当T2 < NL≤T1时为Ⅱ型像素块,该块归类为用于数据嵌入的普通块;当NL≤T2时为Ⅲ型像素块,该块归类为用于进一步分割嵌入的平滑块.
2 基于序列动态选择的可逆信息隐藏算法 2.1 序列动态选择以原始图被分割为u*v且复杂度大于阈值T1的根块BrI为例,其复杂度根据式(8)计算得到.
首先,依据定义1,对BrI像素升序排列得到像素序列{xσ(1),xσ(2),…,xσ(u*v)}.为了更好地在序列动态选择过程中有一个参考标准,引入一个动态选择差值Dadapt(n).
定义7 动态选择差值Dadapt(n)为
| $ D_{\text { adapt }}(n)=x_{\sigma(n)}-x_{\sigma(n-1)}. $ | (9) |
以文献[12]提出的动态二级分块方法为例,根据式(8)可知,复杂度取值范围仅和像素块内经排序得到的序列前后几个像素有关:
| $ \left| {{x_{\sigma (u*v - 4)}} - {x_{\sigma (5)}}} \right| \le NL \le \left| {{x_{\sigma (u*v - 1)}} - {x_{\sigma (2)}}} \right|. $ | (10) |
动态选择的主要对象是复杂度大于阈值T1的复杂块,为了防止在提取端由于复杂度变化而导致块分类产生不可逆的情况出现,在不影响像素点排序序列的基础上,处理后的复杂度NL′必须大于原始复杂度NL.因此,从排序序列中第6个像素xσ(6)开始依序动态选择处理.
由于I-PVO算法对嵌入序列的最值最大修改为1,为了能够在提取处实现可逆还原,引入选择阈值T3,动态选择差值以T3为界限对原序列进行分离.从xσ(6)开始正序检验xσ(r)是否满足:
| $ D_{\text { adapt }}(r) \geqslant T_{3}. $ | (11) |
若在xσ(r)处满足式(11),则该点为某个可动态选择序列的起始位置.然而,当Dadapt(r)=T3时,最值点经I-PVO嵌入操作后可能会导致无法可逆提取,则跳过处理并在位置图中标记为1.其他情况下则对起始位置点xσ(r)实现更新.若直至xσ(u*v-4)始终找不到满足式(11)的位置点,则原始序列不满足动态选择条件,不做任何操作.
然后,从原序列xσ(u*v-4)处开始倒序检验xσ(s+1),寻找该动态选择序列可能的终止位置xσ(s).检查动态选择差值Dadapt(s+1)是否满足:
| $ D_{\text { adapt }}(s+1) \geqslant T_{3}. $ | (12) |
若直至xσ(r+2)始终找不到满足式(12)的位置点,则该序列不满足动态选择条件,不做任何操作.若在xσ(s)处满足式(12),则该点为某个可动态选择序列的结束位置.为了能实现可逆提取,当Dadapt(s+1)=T3时,跳过处理并在位置图中标记为1.其他情况下则对满足条件的子序列{xσ(r),xσ(r+1),…,xσ(s)}进行下一步处理.
定义8 子序列复杂度NL{xσ(r),xσ(r+1),…,xσ(s)}为
| $ N L_{\left\{x_{\sigma(r)}, x_{\sigma(r+1)}, \cdots, x_{\sigma(s)}\right\}}=x_{\sigma(s+1)}-x_{\sigma(r-1)}. $ | (13) |
定义9 子序列复杂度阈值为T4,从而保证子序列嵌入效果.若序列{xσ(r),xσ(r+1),…,xσ(s)}满足:
| $ N L_{\left\{x_{\sigma(r)}, x_{\sigma(r+1)}, \cdots, x_{\sigma(s)}\right\}}<T_{4}, $ | (14) |
则确定为可以嵌入的子序列并在最值处实现I-PVO信息嵌入.若不满足式(14),则利用式(11)、(12)对子序列起止位置r、s依序进行循环更新,若更新到s=r+2仍找不到满足式(14)的序列,则该序列不满足动态选择条件,不做任何操作.
序列动态选择嵌入流程如图 1所示.
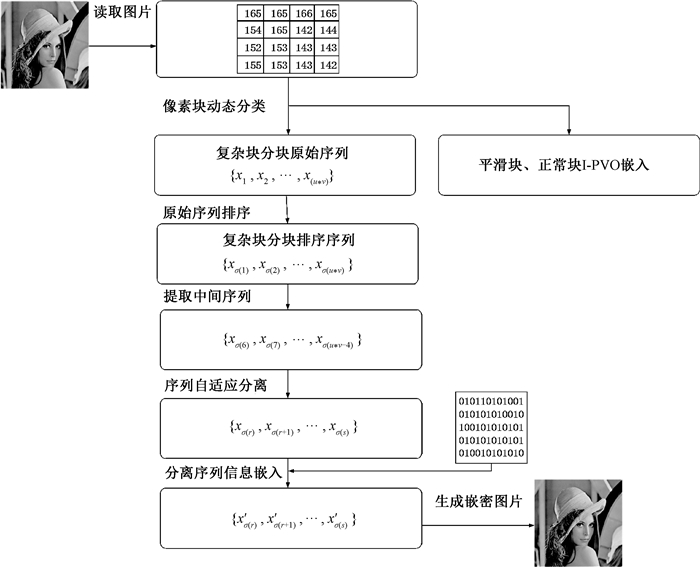
|
图 1 序列动态选择嵌入流程 Fig. 1 Flow chart of sequence dynamic selection embedding |
在信息提取端,利用类似的方法对标记为0的复杂块进行序列动态选择,并在动态选择过程后实现信息提取以及原始序列可逆还原.从x′σ(6)开始依序检验x′σ(r)是否满足式(15),以定位某个动态选择序列的起始位置,
| $ D_{\text { adapt }}^{\prime}(r) \geqslant T_{3}. $ | (15) |
若在x′σ(r)处满足式(15),则对x′σ(r)实现更新.从x′σ(u*v-4)处开始依序检验x′σ(s)是否满足式(16),以定位某个动态选择序列的结束位置,
| $ D_{\text { adapt }}^{\prime}(s+1) \geqslant T_{3}. $ | (16) |
若在x′σ(s)处满足式(16),则对x′σ(s)实现更新.若直至x′σ(r+2)始终找不到满足式(16)的位置点,则该序列不满足动态选择条件,不做任何操作.若在x′σ(s)处满足式(16),则该点为某个可动态选择序列的结束位置.
同样,利用子序列复杂度阈值T4对找到的子序列{x′σ(r),x′σ(r+1),…,x′σ(s)}进行判别,若满足:
| $ N L_{\left\{x_{\sigma(p)}^{\prime}, x_{\sigma(p+1)}^{\prime}, \cdots, x_{\sigma(q)}^{\prime}\right\}}<T_{4}, $ | (17) |
则进行I-PVO信息还原提取.若不满足式(17),则利用式(15)、(16)对子序列起止位置p、q依序进行循环更新,若更新到q=p+2仍找不到满足式(17)的序列,则该序列不满足动态选择条件,不做任何操作.
序列动态选择提取还原流程如图 2所示.
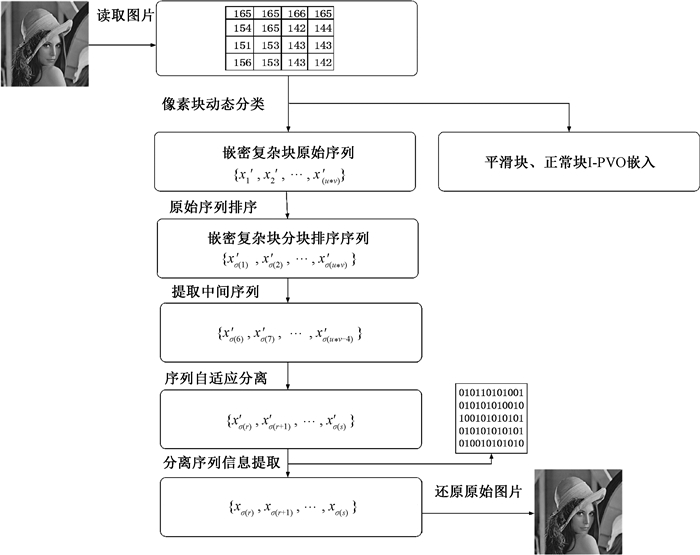
|
图 2 序列动态选择提取还原流程 Fig. 2 Flow chart of sequence dynamic selection extraction and reduction |
根据文献[12]的嵌入要求得到相应的阈值T1、T2.信息嵌入的具体步骤如下.
Step 1 图像分割.将宿主图像分割为一系列大小为u*v的像素块{Br1, Br2, …, Brn}.
Step 2 建立位置图.对于每个像素块,如果其中有任何像素值等于255或0,由于处理过程中会导致溢出,则将这个像素块标记为LM(i)=1.对于其他像素块,标记为LM(i)=0.
Step 3 信息嵌入.依次将数据位嵌入到像素块中,对于每个像素块Br:
如果LM(i)=1,该块的像素点有可能发生溢出,对其不做任何处理.
如果LM(i)=0且NL≤T2,那么该块分割成4个叶块Br={Bi1, Bi2, Bi3, Bi4}.对于每个叶块,利用I-PVO方法进行可逆嵌入.
如果LM(i)=0且T2 < NL≤T1,根据式(5)对根块进行可逆嵌入.
如果LM(i)=0且NL>T1,则该块利用序列动态选择寻找可信息嵌入的子序列,并根据式(5)对动态选择序列进行可逆嵌入.在序列动态选择过程中,为了能够实现无损可逆提取,若满足:
| $ D_{\text { adapt }}(x)=T_{3}, $ | (18) |
则将位置图信息修改为LM(i)=1.
这些步骤反复进行直到所有数据被嵌入,最后一个嵌入数据的像素块用Eb来表示,利用算术编码对处理后的位置图进行无损压缩.
Step 4 嵌入辅助信息和位置图.在原始图的前40+2⌈log2 N⌉+L个像素点的LSB位获得辅助信息和位置图,这些原始信息表示为Slsb,并在这些位中嵌入辅助信息和位置图.这些像素点嵌入的信息分别由以下部分组成:根块大小参数u(4位)和v(4位);块复杂度阈值T1(8位)、T2(8位)、T3(8位)、T4(8位);终止位置Eb(⌈log2 N⌉位);压缩位置图的长度值L(⌈log2 N⌉位);压缩位置图(L位).最终将原始信息Slsb嵌入在终止位置Eb之后的像素块中.
2.2.2 信息提取信息提取的具体步骤如下.
Step 1 辅助信息和位置图提取.读取嵌入信息后图像的前40+2⌈log2 N⌉个像素点的LSB位获得辅助信息,然后再读取接下来L位的LSB获取压缩位置图,通过解压缩处理得到位置图LM.
Step 2 提取Slsb并且实现图像恢复.首先将图像进行像素块分割并计算它们的复杂度,然后在{(BrEb+1)′, …, (BrN)′}块中进行数据提取,对于每个像素块(BrEb+1)′:
如果LM(i)=0且NL≤T2,那么该块分割成4个子块(Br)′={(Bi1)′, (Bi2)′, (Bi3)′, (Bi4)′}.对于每个子块,利用I-PVO方法提取隐藏信息并对原始图像进行恢复.
如果LM(i)=0且T2 < NL≤T1,直接根据式(6)、式(7)提取隐藏信息,并对原始图像进行恢复.
如果LM(i)=0且NL>T1,则该块利用序列动态选择寻找可信息嵌入的子序列,根据式(6)、式(7)提取隐藏信息并对原始图像进行恢复.
如果LM(i)=1,该块没有信息嵌入,对其不做任何处理.
Step 3 数据提取以及图像恢复.将提取的Slsb信息对前40+2⌈log2 N⌉+L个像素点的LSB位进行替换处理.接下来用和Step 2相同的方法对{(Br1)′, …, (BrEb+1)′}像素块进行信息提取,同时实现这些像素块的原始信息恢复,最终实现所有嵌入信息被有效提取并且原始图像得到完全恢复.
3 实验分析为检验算法性能,采用MATLAB2018a进行仿真实验.从USC-SIPI图像库中选取512*512的灰度测试图进行实验,实验过程中对序列最大、最小像素都进行了嵌入操作.
3.1 预测精度分析给定一个宿主图像和一个特定像素块尺寸,可以得到在某个特定复杂度下所有用于信息嵌入的预测误差Net以及对应的非信息嵌入扩展误差Nst.
定义10 预测精度PA为
| $ P A=\frac{N_{e}^{t}}{N_{e}^{t}+N_{s}^{t}}. $ | (19) |
本文算法主要在预测精度较高的动态分类基础上,进一步寻找高精确度的像素位置进行嵌入.为了从复杂度较高的像素块中尽可能动态选择出可嵌中间序列,动态选择阈值T3在满足可逆嵌入条件下要尽可能小,实验过程中将T3设定为3.能够动态选择得到的子序列复杂度必须小于原序列复杂度,将子序列分离阈值T4设定为10会有较好的实验效果.因此在整个实验过程中,将T3设定为3,T4设定为10,对比文献[9]、[11]、[12]中的方法,本文算法在预测精度的总体效果上实现了优化.
嵌入容量设定为5 000 bits时的预测精度如表 1所示.可以看出,本文算法的预测精度比文献[12]平均提高了约2.8%.序列动态选择法对于原本预测精度就很高的图片优化效果不太理想,以F16、House图为例,虽然在预测精度上都比文献[12]减少了约0.2%,但仍分别达到82.68%和91.94%,依旧满足通常信息嵌入的要求.序列动态选择法主要在复杂块上进行信息嵌入,因此对于复杂度较高的图片优化效果明显.以Stream图为例,预测精度比文献[12]优化了约17.7%,大幅度提升了PVO嵌入性能.
|
|
表 1 嵌入容量设定为5 000 bits时的预测精度 Tab. 1 Predict accuracy as embedding capacity was set to 5 000 bits |
对于不同的嵌入容量,本文算法在峰值信噪比衡量指标上整体比文献[9]、[11]、[12]的方法效果更好.在嵌入容量为5 000~20 000 bits,增量为1 000 bits时,各测试图得到的平均峰值信噪比如表 2所示.结果表明,序列动态选择法主要对复杂度较高的图片提升效果明显,以优化效果最好的Stream图为例,本文算法对比3种方法中效果最好的文献[12]方法,峰值信噪比提高了约1.54 dB.
|
|
表 2 测试图的平均峰值信噪比 Tab. 2 Average peak signal to noise ratio of test pictures |
从表 2还可以看出,对于实验所用的测试图,本文算法的峰值信噪比均值比文献[9]、[11]、[12]分别提高了约3.94、2.13、0.23 dB.
3.3 嵌入容量分析序列动态选择能在保证一定预测精度的前提下,寻找具有高预测精度的像素位置进行嵌入,从而在整体上提升了嵌入容量.各测试图对像素点遍历一次后的最大嵌入容量如表 3所示.本文算法对于最大嵌入容量的优化程度与图片复杂度有关,表 3中各图片的复杂度由式(8)计算得到.可以看出,对于复杂度较高的图片,本文算法的最大嵌入容量有一定提升.这是因为复杂度高会导致复杂块个数较多,而复杂块中间序列可以通过动态选择得到合适的嵌入位置,实现了嵌入容量的提升.由于序列动态选择在嵌入过程中需要辅助阈值和嵌入标记,对嵌入容量会有一定影响.从实验数据来看,提升的嵌入容量在一般情况下会大于辅助信息所造成的嵌入损耗.因此,本文算法可以在一定程度上提升最大嵌入容量,特别对根像素块分类后复杂块个数较多的图片提升效果明显.
|
|
表 3 测试图的最大嵌入容量 Tab. 3 Maximum embedding capacity of test pictures |
本文设计并实现了一种基于序列动态选择的PVO可逆信息隐藏算法.算法在动态分块中的复杂块上提出了一种有效的像素处理机制,通过动态选择中间序列预测可嵌像素,在保持图像保真度同时提升嵌入容量.若优化动态分块机制得到更长的像素序列,则能在中间序列中动态选择出更多序列位置进行信息嵌入操作,嵌入性能可以得到进一步提升,这也是下一步需要对本文算法进行改进的方向.
| [1] |
SHI Y Q, LI X L, ZHANG X P, et al. Reversible data hiding: advances in the past two decades[J]. IEEE access, 2016, 4: 3210-3237. DOI:10.1109/ACCESS.2016.2573308 (  0) 0) |
| [2] |
NI Z C, SHI Y Q, ANSARI N, et al. Reversible data hiding[J]. IEEE transactions on circuits and systems for video technology, 2006, 16(3): 354-362. DOI:10.1109/TCSVT.2006.869964 (  0) 0) |
| [3] |
KHAN A, SIDDIQA A, MUNIB S, et al. A recent survey of reversible watermarking techniques[J]. Information sciences, 2014, 279: 251-272. DOI:10.1016/j.ins.2014.03.118 (  0) 0) |
| [4] |
LI X L, ZHANG W M, GUI X L, et al. A novel reversible data hiding scheme based on two-dimensional difference-histogram modification[J]. IEEE transactions on information forensics and security, 2013, 8(7): 1091-1100. DOI:10.1109/TIFS.2013.2261062 (  0) 0) |
| [5] |
WU H Z, WANG H X, SHI Y Q, et al. PPE-based reversible data hiding[C]//Proceedings of the 4th ACM Workshop on Information Hiding and Multimedia Security. Vigo, 2016: 187-188. https://www.researchgate.net/publication/303902035_PPE-Based_Reversible_Data_Hiding
(  0) 0) |
| [6] |
GUI X L, LI X L, YANG B. A high capacity reversible data hiding scheme based on generalized prediction-error expansion and adaptive embedding[J]. Signal processing, 2014, 98(5): 370-380. (  0) 0) |
| [7] |
PENG F, LI X L, YANG B. An adaptive PEE-based reversible data hiding scheme exploiting referential prediction-errors[C]//IEEE International Conference on Multimedia and Expo. Turin, 2015: 1-6. https://www.researchgate.net/publication/308835874_An_adaptive_PEE-based_reversible_data_hiding_scheme_exploiting_referential_prediction-errors
(  0) 0) |
| [8] |
OU B, LI X L, ZHAO Y, et al. Pairwise prediction-error expansion for efficient reversible data hiding[J]. IEEE transactions on image processing, 2013, 22(12): 5010-5021. DOI:10.1109/TIP.2013.2281422 (  0) 0) |
| [9] |
LI X L, LI J, LI B, et al. High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion[J]. Signal processing, 2013, 93(1): 198-205. DOI:10.1016/j.sigpro.2012.07.025 (  0) 0) |
| [10] |
OU B, LI X L, ZHAO Y, et al. Reversible data hiding using invariant pixel-value-ordering and prediction-error expansion[J]. Image communication, 2014, 29(7): 760-772. (  0) 0) |
| [11] |
PENG F, LI X L, YANG B. Improved PVO-based reversible data hiding[J]. Digital signal processing, 2014, 25(2): 255-265. (  0) 0) |
| [12] |
WANG X, DING J, PEI Q Q. A novel reversible image data hiding scheme based on pixel value ordering and dynamic pixel block partition[J]. Information sciences, 2015, 310: 16-35. DOI:10.1016/j.ins.2015.03.022 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


