2. 郑州大学 科学技术信息研究所 河南 郑州 450001
2. Institute of Scientific and Technical Information, Zhengzhou University, Zhengzhou 450001, China
随着电子技术、计算机技术、网络技术和智能化技术的不断发展和完善,智慧图书馆的概念被提出。智慧图书馆是通过数字化、智能化的手段服务读者,它是未来图书馆的发展趋势。智能机器人具备感知、思维和动作三要素,是人工智能技术不可或缺的载体。智能机器人又分为工业机器人和服务机器人两种,图书馆使用的主要是服务机器人[1]。图书馆自动盘点机器人可以有效协助馆员进行盘点、排架工作,降低了人工排架的错误率,近几年来在国内外各大图书馆应用广泛。沈奎林等基于超高频射频识别(radio frequency identification,RFID)技术研制了一种图书自动盘点机器人,并在南京大学图书馆成功试运行[2]。随后,该团队又针对自动盘点机器人在图书馆应用的不足之处,讨论了在情景共融需求下盘点机器人的发展趋势[3]。张宣政设计了一种书库自动盘点机器人,并对机器人的软、硬件进行了详细介绍[4]。黄嘉琪对图书盘点机器人的导航方法进行了详细的研究[5]。夏正伟等以武汉大学为例,介绍了盘点机器人在武汉大学图书馆的应用效果[6]。倪劼对图书盘点智能机器人的结构进行了详细的介绍[7]。
图书自动盘点机器人的路径规划和轨迹跟踪控制是自动盘点机器人能够准确工作的关键技术。传统的图书自动盘点机器人的轨迹跟踪控制方法大多采用比例-积分(proportional-integral, PI)控制方法,由于PI控制方法是一种线性的控制方法,在快速性和准确性之间存在矛盾。近年来,越来越多的非线性控制方法被提出[8-10]。变结构控制又被称为滑模控制,由于其较好的鲁棒性,得到国内外学者的广泛关注[11-12]。由于变结构控制器采用符号函数,存在不连续性,因此其滑模轨迹到达滑模面后会产生“抖震”现象[13]。变结构控制方法的“抖震”只能被抑制,不能够被完全消除,较大的“抖震”会影响图书馆自动盘点机器人的轨迹跟踪效果。为了减少传统变结构的“抖震”现象,需要将变结构控制方法的滑模增益设置减小,较小的滑模增益会影响变结构控制器的响应速度和鲁棒性。因此,如何有效抑制“抖震”,又不影响变结构控制器的响应速度是亟须解决的问题。趋近律方法是一种有效的解决方案[14-15]。
本文针对图书自动盘点机器人轨迹跟踪位置和姿态的双目标控制问题,提出了一种基于改进趋近律的图书自动盘点机器人轨迹跟踪变结构非线性控制方法,通过改进的趋近律,可以有效解决传统变结构控制方法快速性和“抖震”之间的矛盾。
1 图书自动盘点机器人数学模型图书自动盘点机器人融合了物联网技术、计算机图形学、人工智能技术等高新技术,采用RFID技术来实现图书的定位功能。图书自动盘点机器人采用双升降杆,可以实现不同层架的盘点功能。
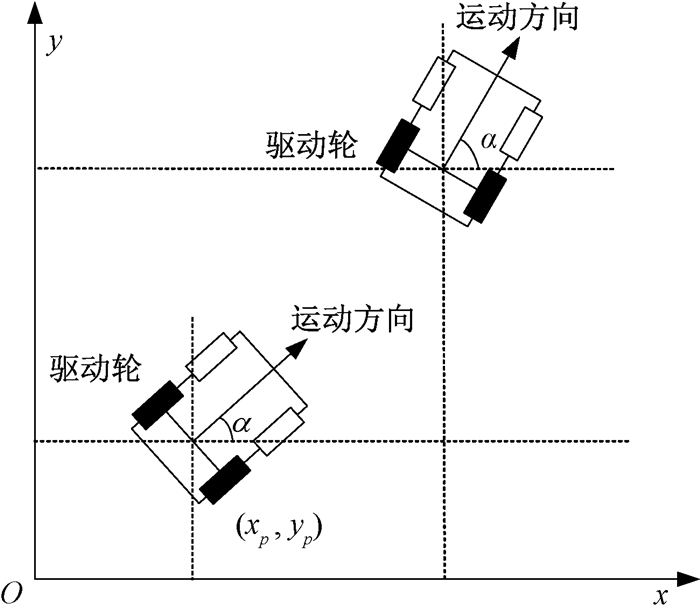
本文以图书自动盘点机器人的底盘为控制对象,研究图书自动盘点机器人的轨迹跟踪控制方法。通过控制左右两侧车轮的速度差,来实现盘点机器人的转弯功能。图书自动盘点机器人的数学模型可以借鉴四轮轮式机器人的建模方法,如图 1所示,图书自动盘点机器人的坐标由机器人底盘驱动轮中点在x轴和y轴坐标系中的位置决定,其姿态由机器人运动方向和x轴的夹角α来表示。
|
图 1 图书自动盘点机器人运动轨迹 Fig. 1 The trajectory of automatic book inventory robot |
由以上描述和图 1可以得到图书自动盘点机器人的运动学方程
| $ \left[\begin{array}{c} x_p^{\prime} \\ y_p^{\prime} \\ \alpha^{\prime} \end{array}\right]=\left(\begin{array}{cc} \cos \alpha & 0 \\ \sin \alpha & 0 \\ 0 & 1 \end{array}\right)\left[\begin{array}{c} v \\ w \end{array}\right], $ | (1) |
其中:x′p、y′p分别为图书自动盘点机器人在x轴和y轴坐标系中的位置;v、w分别为盘点机器人的线速度和角速度。由公式(1)可知,该系统为欠驱动系统,因此,该系统的轨迹跟踪控制问题需要设计控制率实现图书自动盘点机器人的位置跟踪和姿态随动。
2 图书盘点机器人变结构轨迹跟踪及趋近律设计变结构控制(variable structure control, VSC)也叫滑模控制(sliding mode control, SMC),其本质是一种非线性控制方法[16-18]。其原理是通过系统所期望的动态轨迹来设计滑模面,通过控制系统变量最终到达滑模面来实现对期望目标的控制。因此,VSC具有较强的鲁棒性。由于VSC对被控对象的模型误差、被控对象参数的变化和外部干扰不敏感,将该方法应用于图书自动盘点机器人轨迹跟踪控制,具有一定的优越性。然而,由于变结构控制中存在不连续的符号函数,因此变结构控制存在“抖震”现象。较小的滑模增益可以削弱“抖震”,但是其鲁棒性也同样被削弱。因此,变结构控制方法削弱“抖震”和提高鲁棒性是矛盾的。本节内容提出了一种改进的变结构趋近律,可以有效解决传统变结构控制方法快速性和“抖震”之间的矛盾。
2.1 改进变结构趋近律传统变结构控制方法,大多采用等速趋近律,等速趋近律的定义为
| $ \frac{s(t+1)-s(t)}{T_s}=-k \operatorname{sgn}(s(t)), $ | (2) |
其中:s为滑模面;Ts为采样时间;k为滑模增益。将采样时间移至方程右边,可以得到
| $ s(t+1)-s(t)=-k T_s \operatorname{sgn}(s(t)) 。$ | (3) |
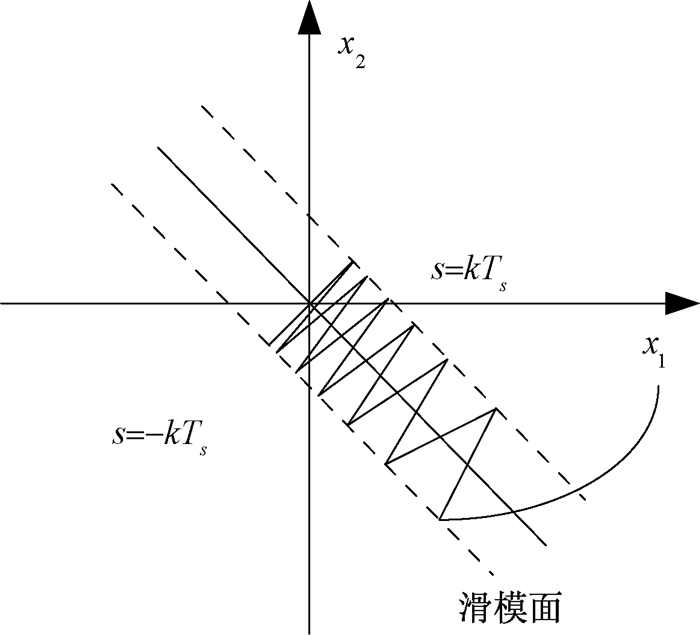
系统轨迹从s>0侧到达滑模面后,由公式(3)可以得到,s(t+1)=-kTs;当系统轨迹从s < 0侧到达滑模面后,由公式(3)可以得到,s(t+1)=kTs。因此,在系统轨迹到达滑模面后,会发生“抖震”现象,其切换带宽为kTs。k较大时,滑模增益较大,具有更强的鲁棒性,但是其切换带宽也随之增大,“抖震”现象也更强烈。传统等速趋近律的状态轨迹如图 2所示。
|
图 2 传统等速趋近律的状态轨迹图 Fig. 2 The trajectory of traditional constant rate reaching law |
为了克服传统等速趋近率切换带宽和趋近速度矛盾的问题,提出了一种改进的变结构趋近率,改进趋近率为
| $ \begin{aligned} & \frac{s_1(t+1)-s_1(t)}{T_s}= \\ & \begin{cases}-\frac{k_s}{\lambda} \operatorname{sgn}\left(s_1(t)\right), & \left|x_1(t)\right|>\delta, \\ -k_s\left(\left|x_1(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_1(t)\right), & \left|x_1(t)\right| \leqslant \delta, \end{cases} \end{aligned} $ | (4) |
其中:s1为滑模面;Ts为采样时间;ks为滑模增益;γ为负实数;0 < λ < 1;β为正整数。当系统轨迹远离滑模面时,通过选取λ,可以得到较大的滑模增益。
当系统轨迹从s1>0侧到达滑模面后,
| $ s_1(t+1)=\frac{-k_s\left|x_1(t)\right|^{-\gamma}}{1+\beta\left|x_1(t)\right|^{-\gamma}} \text { 。} $ | (5) |
当系统轨迹从s1 < 0侧到达滑模面后,
| $ s_1(t+1)=\frac{k_s\left|x_1(t)\right|^{-\gamma}}{1+\beta\left|x_1(t)\right|^{-\gamma}} \text { 。} $ | (6) |
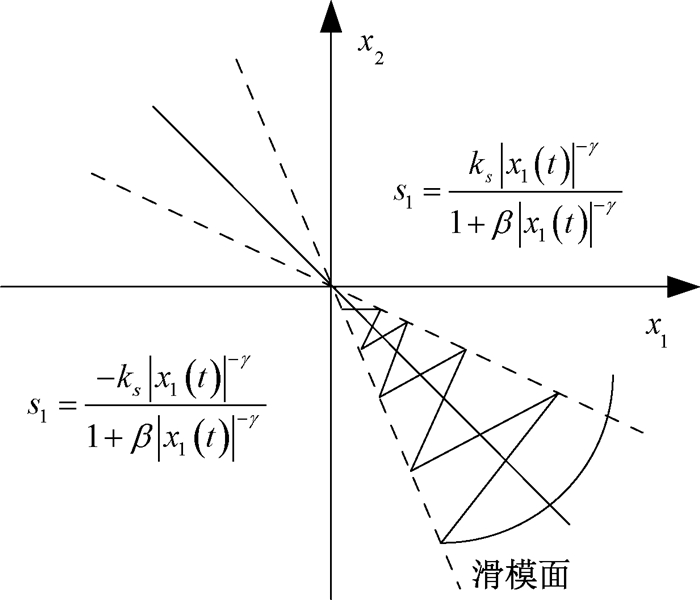
因此,基于这种改进的变结构趋近率,系统轨迹到达滑模面后,其切换带宽会随着状态变量x1的绝对值变小而逐渐减小,从而达到对“抖震”的抑制作用。改进变结构趋近率的状态轨迹如图 3所示。
|
图 3 改进变结构趋近律的状态轨迹图 Fig. 3 The trajectory of proposed reaching law |
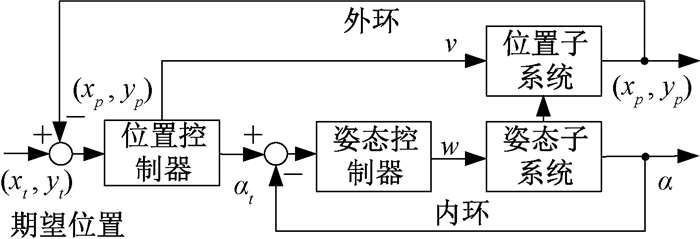
基于改进趋近率的图书盘点机器人变结构轨迹跟踪控制器采用双闭环控制结构,姿态控制器为内环,位置控制器为外环,位置控制器的输出角度αt为内环姿态控制器参考角度。外环位置控制器小于内环姿态控制器的收敛速度,通过盘点机器人实际输出角度α快速跟踪αt,保证闭环系统的稳定性。基于双闭环控制结构的盘点机器人轨迹跟踪控制框图如图 4所示。
|
图 4 基于双闭环控制结构的盘点机器人轨迹跟踪控制框图 Fig. 4 Control block diagram of inventory robot trajectory tracking based on double closed-loop control structure |
根据2.1提出的改进变结构趋近率来设计盘点机器人的姿态控制器,实现角度α跟踪目标角度αt。根据角度的误差e=x1=α-αt,角度误差的导数为e′=x2=w-α′t。
设计变结构滑模面,可以得到
| $ s_3=c_1 x_1+x_2 。$ | (7) |
对公式(7)求导,离散化后可以得到
| $ \begin{aligned} & \frac{s_3(t+1)-s_3(t)}{T_s}= \\ & c_1 w(t)-c_1 \frac{\alpha_t(t+1)-\alpha_t(t)}{T_s}+\frac{x_2(t+1)-x_2(t)}{T_s}= \\ & \begin{cases}-\frac{k_1}{\lambda_1} \operatorname{sgn}\left(s_3(t)\right), & \left|x_1(t)\right|>\delta_1, \\ -k_1\left(\left|x_1(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_3(t)\right), & \left|x_1(t)\right| \leqslant \delta_{10} 。\end{cases} \end{aligned} $ | (8) |
通过公式(8),可以得到盘点机器人的姿态控制器为
| $ w(t)=\left\{\begin{array}{l} -\frac{k_1}{c_1 \lambda_1} \operatorname{sgn}\left(s_3(t)\right)+\frac{\alpha_t(t+1)-\alpha_t(t)}{T_s} \\ \frac{x_2(t+1)-x_2(t)}{c_1 T_s}, \left|x_1(t)\right|>\delta_1, \\ -\frac{k_1}{c_1}\left(\left|x_1(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_3(t)\right)+ \\ \frac{\alpha_t(t+1)-\alpha_t(t)}{T_s}-\frac{x_2(t+1)-x_2(t)}{c_1 T_s}, \\ \left|x_1(t)\right| \leqslant \delta_1 。\end{array}\right. $ | (9) |
盘点机器人的外环采用位置控制器,实现机器人的位置跟踪功能。由盘点机器人的运动学方程(1)展开,可以得到
| $ \left\{\begin{array}{l} x_p^{\prime}=v \cos \alpha, \\ y_p^{\prime}=v \sin \alpha, \\ \alpha^{\prime}=w 。\end{array}\right. $ | (10) |
盘点机器人的位置误差为
| $ \left\{\begin{array}{l} x_e=x_p-x_t, \\ y_e=y_p-y_t 。\end{array}\right. $ | (11) |
设计盘点机器人位置控制器的变结构滑模面为
| $ \left\{\begin{array}{l} s_4=c_2 x_e+x_e^{\prime} \\ s_5=c_3 y_e+y_{e }^{\prime}。\end{array}\right. $ | (12) |
对公式(12)求导,并将本文所提出的变结构趋近率公式(4)代入,离散化后可以得到
| $ \begin{aligned} & \frac{s_4(t+1)-s_4(t)}{T_s}=c_2 v \cos \alpha-c_2 \frac{x_t(t+1)-x_t(t)}{T_s}+ \\ & \frac{x_e(t+2)-2 x_e(t+1)+x_e(t)}{T_s^2}= \\ & \begin{cases}-\frac{k_2}{\lambda_2} \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right|>\delta_2, \\ -k_2\left(\left|x_e(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right| \leqslant \delta_2 。\end{cases} \end{aligned} $ | (13) |
| $ \begin{aligned} & \frac{s_4(t+1)-s_4(t)}{T_s}=c_2 v \cos \alpha-c_2 \frac{x_t(t+1)-x_t(t)}{T_s}+ \\ & \frac{x_e(t+2)-2 x_e(t+1)+x_e(t)}{T_s^2}= \\ & \begin{cases}-\frac{k_2}{\lambda_2} \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right|>\delta_2, \\ -k_2\left(\left|x_e(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right| \leqslant \delta_2 。\end{cases} \end{aligned} $ | (14) |
令u1=vcosα,u2=vsinα,通过式(13)、(14),可以得到盘点机器人的外环变结构位置控制器,
| $ {u_1}(t) = \left\{ {\begin{array}{*{20}{l}} { - \frac{{{k_2}}}{{{c_2}{\lambda _2}}}{\mathop{\rm sgn}} \left( {{s_4}(t)} \right) + \frac{{{x_t}(t + 1) - {x_t}(t)}}{{{T_s}}} - }\\ \begin{array}{l} \frac{{{x_e}(t + 2) - 2{x_e}(t + 1) + {x_e}(t)}}{{{c_2}T_s^2}},\\ \;\;\;\left| {{x_e}(t)} \right| > {\delta _2}, \end{array}\\ { - \frac{{{k_e}}}{{{c_2}}}{{\left( {{{\left| {{x_e}(t)} \right|}^\gamma },\beta } \right)}^{ - 1}}{\mathop{\rm sgn}} \left( {{s_4}(t)} \right) + }\\ {\frac{{{x_t}(t + 1) - {x_t}(t)}}{{{T_s}}} - \frac{{{x_e}(t + 2) - 2{x_e}(t + 1) + {x_e}(t)}}{{{c_2}T_s^2}},}\\ {\left| {{x_e}(t)} \right| \le {\delta _2},} \end{array}} \right. $ | (15) |
| $ u_2(t)=\left\{\begin{array}{l} -\frac{k_3}{c_3 \lambda_3} \operatorname{sgn}\left(s_5(t)\right)+\frac{y_t(t+1)-y_t(t)}{T_s}- \\ \frac{y_e(t+2)-2 y_e(t+1)+y_e(t)}{c_3 T_s^2}, \\ \left|y_e(t)\right|>\delta_3,\\ -\frac{k_3}{c_3}\left(\left|y_e(t)\right|^\gamma+\beta\right)^{-1} \operatorname{sgn}\left(s_5(t)\right)+ \\ \frac{y_t(t+1)-y_t(t)}{T_s}-\frac{y_e(t+2)-2 y_e(t+1)+y_e(t)}{c_3 T_s^2}, \\ \left|y_e(t)\right| \leqslant \delta_3 。\end{array}\right. $ | (16) |
由u1=vcos α,u2=vsin α,可得
| $ \tan \alpha=\frac{u_2}{u_1}, $ | (17) |
α取值(-π/2, π/2),可得
| $ \alpha=\arctan \frac{u_2}{u_1} 。$ | (18) |
α为位置控制率所期望的角度,如果α=αt,则式(15)和式(16)等价。但是,实际模型α≠αt,特别是在控制系统初始阶段。因此,需要设定式(18)的角度为理想值,通过内环控制器快速收敛,使角度α快速跟踪αt,保证闭环系统的稳定性[19],
| $ \alpha_t=\arctan \frac{u_2}{u_1} 。$ | (19) |
因此,盘点机器人的外环变结构位置控制器为
| $ v=\frac{u_1}{\cos \alpha_t}。$ | (20) |
由式(7)可知,定义李雅普诺夫函数
| $ V_1=\frac{s_3^2}{2}, $ | (21) |
对式(21)求导,联合式(8),可得
| $ \begin{aligned} & V_1^{\prime}=s_3 s_3^{\prime}= \\ & \begin{cases}-\frac{k_1}{\lambda_1} s_3 \operatorname{sgn}\left(s_3(t)\right), & \left|x_1(t)\right|>\delta_1, \\ -k_1\left(\left|x_1(t)\right|^\gamma+\beta\right)^{-1} s_3 \operatorname{sgn}\left(s_3(t)\right), & \left|x_1(t)\right| \leqslant \delta_1, \end{cases} =\\ & \begin{cases}-\frac{k_1}{\lambda_1}\left|s_3(t)\right|, & \left|x_1(t)\right|>\delta_1, \\ -k_1\left(\left|x_1(t)\right|^\gamma+\beta\right)^{-1}\left|s_3(t)\right|, & \left|x_1(t)\right| \leqslant \delta_1, \end{cases} \end{aligned} $ | (22) |
其中:0 < λ < 1;β为正整数;γ为负实数。因此,由式(22)可得
| $ V_1^{\prime} \leqslant 0。$ | (23) |
根据李雅普诺夫稳定性理论可以得知,闭环系统在所设计的盘点机器人姿态控制器下是稳定的。
2.3.2 位置控制器稳定性分析由式(12)可知,定义x轴、y轴控制器的李雅普诺夫函数分别为V2和V3,
| $ \left\{\begin{array}{l} V_2=\frac{s_4^2}{2}, \\ V_3=\frac{s_5^2}{2}。\end{array}\right. $ | (24) |
对式(24)求导,联合式(13)、(14),可得
| $ \begin{aligned} & V_2^{\prime}=s_4 s_4^{\prime}= \\ & \left\{\begin{array}{ll} -\frac{k_2}{\lambda_2} s_4 \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right|>\delta_2, \\ -k_2\left(\left|x_e(t)\right|^\gamma+\beta\right)^{-1} s_4 \operatorname{sgn}\left(s_4(t)\right), & \left|x_e(t)\right| \leqslant \delta_2, \end{array}=\right. \\ & \begin{cases}-\frac{k_2}{\lambda_2}\left|s_4\right|, & \left|x_e(t)\right|>\delta_2, \\ -k_2\left(\left|x_e(t)\right|^\gamma+\beta\right)^{-1} s_4\left|s_4\right|, & \left|x_e(t)\right| \leqslant \delta_2, \end{cases} \\ & \end{aligned} $ | (25) |
| $ \begin{aligned} & V_3^{\prime}=s_5 s_5^{\prime}= \\ & \begin{cases}-\frac{k_3}{\lambda_3} s_5 \operatorname{sgn}\left(s_5(t)\right), & \left|y_e(t)\right|>\delta_3, \\ -k_3\left(\left|y_e(t)\right|^\gamma+\beta\right)^{-1} s_5 \operatorname{sgn}\left(s_5(t)\right), & \left|y_e(t)\right| \leqslant \delta_3, \end{cases}= \\ & \begin{cases}-\frac{k_3}{\lambda_3}\left|s_5\right|, & \left|y_e(t)\right|>\delta_3, \\ -k_3\left(\left|y_e(t)\right|^\gamma+\beta\right)^{-1}\left|s_5\right|, & \left|y_e(t)\right| \leqslant \delta_3, \end{cases} \\ & \end{aligned} $ | (26) |
其中:0 < λ < 1;β为正整数;γ为负实数。因此,由公式可得
| $ \left\{\begin{array}{l} V_2^{\prime} \leqslant 0, \\ V_3^{\prime} \leqslant 0。\end{array}\right. $ | (27) |
根据李雅普诺夫稳定性理论可以得知,闭环系统在所设计的盘点机器人位置控制器下是稳定的。
3 仿真验证为了验证所提出算法的控制效果,本文将所提出的改进趋近率变结构双闭环控制算法和传统基于等速趋近率的变结构双闭环控制算法进行对比研究,其中传统基于等速趋近率的变结构双闭环控制算法取不同的增益数值。仿真环境基于Matlab\Simulink 2021a。硬件基于联想的工作站Think Center M920t。CPU为酷睿i7-8700,3.2 GHz;硬盘为M.2 PCIe高速SSD;显卡为RX550X 4 GB独显。基于等速趋近率的变结构控制方法,内环滑模增益分别设置为kd1=3和kd1=0.1, 外环滑模增益设置为kd2=3, kd3=5。
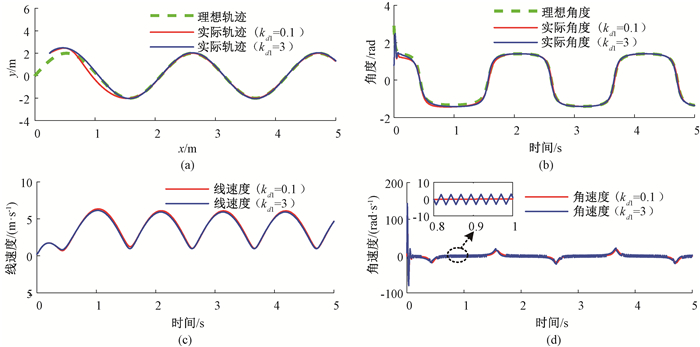
图 5为kd1=3和kd1=0.1时,基于等速趋近率的盘点机器人轨迹跟踪控制结果。从图 5(a)中可以看出,基于等速趋近率的变结构控制方法,当kd1=3时,控制方法具有较快的趋近速度,盘点机器人的实际运行轨迹可以快速跟踪理想轨迹。当kd1=0.1时,基于等速趋近率的变结构控制方法趋近速度比kd1=3时的趋近速度慢,图书智能盘点机器人跟踪理想轨迹的响应时间较长。图 5(d)为图书智能盘点机器人角速度图。可以看出,当kd1=0.1时,基于等速趋近率的变结构控制方法趋近速度较慢。但是,较小的滑模增益对“抖震”具有较好的抑制作用。因此,基于等速趋近率的变结构控制方法存在快速性和“抖震”之间矛盾的问题。
|
图 5 基于等速趋近率的盘点机器人轨迹跟踪控制 Fig. 5 Trajectory tracking control of inventory robot based on traditional constant rate reaching law |
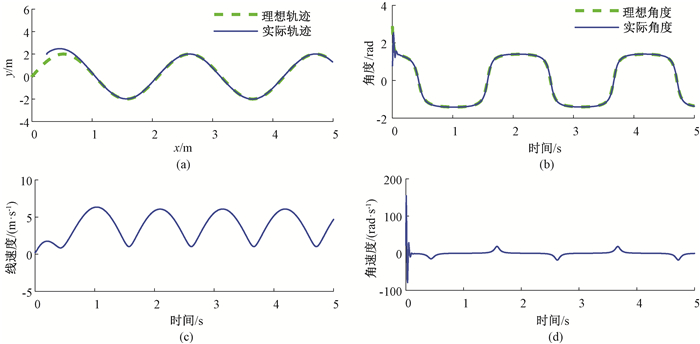
图 6为基于改进趋近率的盘点机器人轨迹跟踪控制的仿真结果图。变结构改进趋近率的参数为γ=-1,λ1=0.2, λ2=0.2, λ3=0.2, β=3, k1=3, k2=1, k3=0.6, δ1=0.01, δ2=0.01, δ3=0.1,c1=0.01, c2=0.01, c3=0.01。从图 6可以看出,基于改进趋近率的盘点机器人轨迹跟踪控制方法,不仅有较快的趋近速度,还可以有效抑制“抖震”,具有较好的控制效果。
|
图 6 基于改进趋近率的盘点机器人轨迹跟踪控制 Fig. 6 Trajectory tracking control of inventory robot based on proposed reaching law |
本文针对图书自动盘点机器人轨迹跟踪位置和姿态的双目标控制问题,提出了一种基于改进趋近律的图书自动盘点机器人轨迹跟踪变结构非线性控制方法。本文所提出的改进的趋近率,通过动态调节系统轨迹远离滑模面和到达滑模面之后的增益大小,有效解决传统变结构控制方法快速性和“抖震”之间矛盾的问题,并将本文提出的方法和传统变结构控制方法进行对比验证。结果表明,所提出的方法不仅具有较快的响应速度,还对“抖震”有较好的抑制作用。
| [1] |
焦洁. 图书馆智能机器人应用研究[D]. 郑州: 郑州大学, 2020. JIAO J. Research on the application of library intelligent robot[D]. Zhengzhou: Zhengzhou University, 2020. (  0) 0) |
| [2] |
沈奎林, 邵波, 陈力军, 等. 基于超高频RFID的图书盘点机器人的设计和实现[J]. 图书馆学研究, 2016(7): 24-28. SHEN K L, SHAO B, CHEN L J, et al. The design and implementation of book inventory robot based on ultra high frequency RFID[J]. Research on library science, 2016(7): 24-28. (  0) 0) |
| [3] |
沈奎林, 邵波, 陈力军. 情景共融环境下图书馆盘点机器人的发展研究[J]. 图书馆研究, 2020, 50(5): 98-102. SHEN K L, SHAO B, CHEN L J. Research on the development of library inventory robot in situational integration environment[J]. Library research, 2020, 50(5): 98-102. (  0) 0) |
| [4] |
张宣政. 书库自动盘点机器人小车设计研究[D]. 上海: 华东理工大学, 2016. ZHANG X Z. The design and research about the automatic inventory smart car in stack room[D]. Shanghai: East China University of Science and Technology, 2016. (  0) 0) |
| [5] |
黄嘉琪. 图书盘点机器人自主导航方法研究及系统实现[D]. 南京: 南京大学, 2018. HUANG J Q. Research on robotic navigation for bookshelf scanning robot[D]. Nanjing: Nanjing University, 2018. (  0) 0) |
| [6] |
夏正伟, 李全, 端文慧, 等. RFID图书自动盘点机器人应用研究: 以武汉大学图书馆为例[J]. 图书馆杂志, 2020, 39(1): 61-66. XIA Z W, LI Q, DUAN W H, et al. Research on the application of RFID automated inventory robot: a case study of Wuhan university library[J]. Library journal, 2020, 39(1): 61-66. (  0) 0) |
| [7] |
倪劼. RFID图书盘点智能机器人的设计与开发[J]. 新世纪图书馆, 2017(2): 69-72. NI J. Design and development of RFID intelligent book inventory robots[J]. New century library, 2017(2): 69-72. (  0) 0) |
| [8] |
颜佳晴, 鲁聪达, 蔡颖杰, 等. 基于积分模型预测控制的全向移动机器人轨迹跟踪研究[J]. 高技术通讯, 2021, 31(10): 1081-1089. YAN J Q, LU C D, CAI Y J, et al. Research on trajectory tracking of omnidirectional mobile robot based on integral model predictive control[J]. Chinese high technology letters, 2021, 31(10): 1081-1089. (  0) 0) |
| [9] |
樊茂, 汤亮. 空间机器人抓捕碰撞分析与轨迹规划镇定控制[J]. 宇航学报, 2021, 42(10): 1305-1316. FAN M, TANG L. Impact analysis and trajectory planning stabilization control for space robot after capturing target[J]. Journal of astronautics, 2021, 42(10): 1305-1316. (  0) 0) |
| [10] |
杨国东, 刘泓滨, 刘碧飞. 四轮移动机器人的模糊滑模轨迹跟踪控制[J]. 农业装备与车辆工程, 2021, 59(9): 38-42. YANG G D, LIU H B, LIU B F. Fuzzy sliding mode trajectory tracking control of four-wheel mobile robot[J]. Agricultural equipment & vehicle engineering, 2021, 59(9): 38-42. (  0) 0) |
| [11] |
肖光飞, 胡秋霞, 韩磊, 等. 基于滑模变结构的轮式机器人双环轨迹跟踪控制[J]. 机械设计与制造, 2020(4): 244-247. XIAO G F, HU Q X, HAN L, et al. The double-loops trajectory tracking control of wheeled mobile robot based on sliding mode variable structure[J]. Machinery design & manufacture, 2020(4): 244-247. (  0) 0) |
| [12] |
贺倩, 黄宴委. 基于非奇异终端滑模控制的水面无人船轨迹跟踪[J]. 电工技术, 2021(10): 39-42. HE Q, HUANG Y W. Trajectory tracking of unmanned surface ships based on non-singular terminal sliding mode control[J]. Electric engineering, 2021(10): 39-42. (  0) 0) |
| [13] |
ZHANG X G, SUN L Z, ZHAO K, et al. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE transactions on power electronics, 2013, 28(3): 1358-1365. (  0) 0) |
| [14] |
WANG Y Q, FENG Y T, ZHANG X G, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE transactions on power electronics, 2020, 35(4): 4117-4126. (  0) 0) |
| [15] |
JUNEJO A K, XU W, MU C X, et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE transactions on power electronics, 2020, 35(11): 12110-12121. (  0) 0) |
| [16] |
WANG Q, YU H T, WANG M, et al. An improved sliding mode control using disturbance torque observer for permanent magnet synchronous motor[J]. IEEE access, 7: 36691-36701. (  0) 0) |
| [17] |
张晓光. 永磁同步电机调速系统滑模变结构控制若干关键问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. ZHANG X G. Research on key issuses of permanent magnet sysnchronous motor sliding mode speed control system[D]. Harbin: Harbin Institute of Technology, 2014. (  0) 0) |
| [18] |
CHEN X G, LI Y M, MA H F, et al. A novel variable exponential discrete time sliding mode reaching law[J]. IEEE transactions on circuits and systems Ⅱ: express briefs, 2021, 68(7): 2518-2522. (  0) 0) |
| [19] |
刘金琨. 滑模变结构控制MATLAB仿真基本理论与设计方法[M]. 北京: 清华大学出版社, 2015. LIU J K. Sliding mode control design and MATLAB simulation[M]. Beijing: Tsinghua University Press, 2015. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55

