2. 山西大学 计算智能与中文信息处理教育部重点实验室 山西 太原 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006, China
现实领域中,很多场景下样本不仅仅对应单一语义。例如图像标注领域[1],一幅图片可能具有多个标注概念;文本分类领域[2],一件新闻事件可能同时具有多个主题;生物工程领域[3],一个蛋白质可能同时具有多种生物功能。传统单标记监督方法已不能很好地解决多语义问题,为此多标记学习框架被提出。不同于单标记学习,多标记学习中一个样本对应一个非空标记集合,其丰富的标记概念往往需要高维的特征空间描述,因此特征维度灾难已是多标记学习的重要挑战之一[4]。
在多标记学习中,特征高维问题一方面使得学习算法具有较高的时间和空间复杂度,另一方面,也降低了学习器的精度和泛化能力,甚至造成过拟合现象。为此已有大量多标记降维方法被提出。同单标记学习一样,多标记降维方法大致分为两类,一类为多标记特征抽取方法[5-7],另一类为多标记特征选择方法。特征抽取是指对原始特征空间进行特定组合(线性组合)将其映射到一个低维空间,该类方法通常可以有效降维并取得不错的分类效果,但是不能保留原始特征的物理意义,对应分类过程不具有解释性。而现实领域中的很多问题,往往需要更好的解释性,例如医疗领域,好的解释性有助于医生更好地运用模型;金融领域,好的解释性有助于金融公司了解为用户推荐基金的原因。相较于特征抽取,特征选择方法不仅可以有效去除特征空间中冗余、无关特征,而且可以保留原始特征的物理意义,具有更好的解释性,为此多标记特征选择已成为一项重要研究课题。近年来,已有大量多标记特征选择算法被提出,在很大程度上降低了维度灾难对于多标记学习的影响。与单标记特征选择不同,多标记特征选择需要综合考虑特征与多个标记之间的关系,同时需要考虑标记之间的相关性。对多标记特征选择的研究主要包括,怎样构建合适的特征选择框架和怎样定义特征与标记集相关性的度量。现有的多标记特征选择可以从4个角度进行归类。
1) 从数据转换角度,现有多标记特征选择算法可分为:转化法、直接法。转化法是指将多标记问题转化为单标记问题,进而可直接运用已有单标记特征选择方法。直接法是指对现有特征选择方法进行改进,例如构建新的多元度量、运用矩阵稀疏范数等方法。
2) 从特征选择过程与学习器的联系出发,考虑到多标记特征选择是否依赖于特定学习器,现有多标记特征选择算法可分为:过滤式、包裹式、嵌入式三种。
3) 从不同标记特征子集的共享程度出发,考虑到不同标记可能拥有不同的特征子集,现有多标记特征选择算法可分为:标记共享式、标记粒化式、标记专属式三种。
4) 从数据的应用场景出发,考虑到现实多标记数据会存在动态更新现象,现有多标记特征选择算法可分为:非增量式、增量式。
本文将从以上4种不同角度对多标记特征选择方法进行归类论述,并具体介绍各类方法的相关理论及具体方法,分析各类方法优缺点,进而对多标记特征选择方法的进一步研究进行总结。
1 数据转化多标记数据可通过不同方式转为单标记数据,包括将多标记问题转为多个二分类问题或将多标记问题转为一个多分类问题,这些转化方法已在多标记分类中得到很好应用,可以直接运用已有单标记分类算法解决多标记分类问题。多标记特征选择同样也可以转化为具体的单标记特征选择。从数据转化角度分析,现有多标记特征选择算法可归为:基于标记幂集的多标记特征选择(label powerset multi-label feature selection, LP_MLFS);基于二值相关的多标记特征选择(binary relevance multi-label feature selection, BR_MLFS);非转化多标记特征选择(directed multi-label feature selection, Direct_MLFS)。
1.1 基于标记幂集的多标记特征选择最直接的转化方法为标记幂集方法(label power set,LP)[8],这类方法的主要思想是将多标记数据中的每一种标记组合看作一种类别,将多标记数据转化为一个多类别单标记数据,例如表 1到表 2的转化;然后运用单标记特征选择算法选出重要特征子集。接下来,首先介绍LP以及它的改进方法PPT(pruned problem transformation),然后介绍一些基于LP的多标记特征选择方法。
|
|
表 1 多标记数据 Tab. 1 Multi-label data |
|
|
表 2 多类别数据 Tab. 2 Multi-class data |
LP最初被提出用于解决多标记分类,这种转化方法有效考虑了标记相关性,但是也存在两个比较大的问题。一类问题是,该方法转化所得数据类别数与标记个数呈指数关系,并且类别往往不平衡,分类效果不太理想。另一类问题是,由于训练集数量有限,并非所有可能的组合类别都出现在训练集中,因此LP的预测结果仅局限于训练集中已出现类别,不具有好的泛化能力。
针对LP在转化过程中数据类别数与标记个数呈指数关系的问题,文献[9]提出一种新的转化方法PPT,该方法运用剪枝策略,在LP的基础上,通过设置最小类别数阈值,过滤掉出现频率小的类别数据,有效避免了LP方法中类别多、类别不平衡问题。
基于LP转化方法,已有大量多标记特征选择算法被提出。文献[10]在音乐情感识别多标记任务中,首先基于LP方法将多标记数据转化为单标记数据,然后运用单标记卡方检验方法对转换后数据进行特征选择,实验展示了该方法的有效性。文献[11]提出一种基于PPT转化的多标记特征选择算法,首先应用PPT转化策略将多标记数据转为单标记数据,然后基于互信息运用启发式搜索策略对转化后数据进行特征选择,实验验证了该方法的有效性。文献[12]将PPT转化策略和ReliefF算法相结合构建了一种新的多标记特征选择算法。
1.2 基于二值相关的多标记特征选择二值相关(binary relevance,BR)法可以将多标记数据转化为多个二分类数据[1],已在多标记分类中得到有效运用,也被运用于多标记特征选择。需要注意的是,本文所介绍的BR方法在文献[13]中归为external approach BR方法,本文将从标记是否共享特征的角度详细介绍。基于BR转化的多标记特征选择主要思想是,首先将多标记数据转为多个二分类数据;然后运用单标记特征选择算法对每个二分类数据进行特征排序;最后根据某种融合策略对所得多个排序序列进行融合,得出合适的特征排序或特征子集。
文献[14]提出了随机“k-标记集”(random k-label sets, RAKEL)多标记分类方法。作者首先基于BR转化策略将多标记数据转化为多个二分类数据;然后运用卡方检验得出每个二分类数据的特征排序;最后运用融合策略选出最终的特征子集,有效提高了RAKEL算法的分类效率。
文献[15]分别应用BR和LP策略对多标记数据进行转换,运用信息增益和ReliefF度量对特征进行评价,并给出了4种算法的对比结果,分析了不同算法和不同度量的优势与缺点。
1.3 非转化多标记特征选择将多标记数据转化为单标记数据,再运用已有特征选择方法对转化后的单标记数据进行特征选择,转化过程往往会造成一些信息的损失或转化本身会存在一些问题,直接对多标记数据进行特征选择是一种更加自然的方法[16-22]。这类方法主要思想是运用或构建多元变量相关性度量或借助一些矩阵稀疏化方法等。
文献[16]首次将ReliefF算法应用于多标记特征选择。文献[17]对ReliefF度量进行改进以便适用于多标记特征选择,该方法不同于上面所介绍的转化类方法,不需要将多标记数据转化为单标记数据,而是引入汉明距离作为样本之间不相似性度量,去计算样本之间的最近邻样本,进而使ReliefF算法能有效对多标记数据进行特征选择。
文献[18]提出一种基于多元互信息多标记特征选择(pairwise multivariate mutual information, PMU)算法,该方法首先给出了高维联合熵的近似计算方法;然后运用多元互信息度量特征子集与标记集之间的相关性,运用前向贪心策略对特征进行排序,并根据给定选择特征个数获得了对应的特征子集。
文献[19]提出一种快速多标记特征选择算法,首先从理论上分析了PMU算法中基于互信息的特征得分函数具有较高时间复杂度,提出三种加速策略:丢弃得分函数中非必要计算项;重用预计算熵项;识别有效标记对。实验展示了该算法相比于其他多标记特征选择算法具有更高效率。
文献[20]提出一种新的基于互信息的多标记特征选择算法,定义了一种新的得分函数,相比于PMU中只考虑二阶交叉信息,该函数能够考虑任意程度的交叉信息。文中也从理论上分析了考虑低阶交叉信息的得分函数为何可以获得有效的特征子集,实验结果也表明考虑高阶交叉信息的得分函数反而具有较高计算成本和更低的分类性能。
PMU算法在处理大规模多标记时,会随标记规模增加而不能很好地考虑特征间的冗余性,很容易引入冗余特征。文献[21]给出一种新的特征度量准则,有效避免处理大规模标记时,偏重于考虑最大化相关性,而不能很好地考虑最小冗余性的问题,提出了一种处理大规模标记的多标记特征选择。与传统的多标记特征选择方法相比,该方法在处理大规模多标记数据时取得了更好的效果。
文献[22]基于帕累托优势概念提出一种快速的多标记特征选择算法,将多标记特征选择问题作为多目标优化问题,首先运用对称不确定性(symmetrical uncertainty, SU)度量每个特征与每个标记的相关性,依据帕累托优势概念,特征集被划分为可支配特征集和非支配特征集,将非支配特征集作为约简子集。
现有的多标记特征选择方法大多属于非转换式方法,接下来本文会从特征选择过程与学习器的联系角度进行更多的介绍。
1.4 各类方法对比无论是基于转化还是直接的多标记特征选择,都在一定程度上降低了特征维度,提高了算法的效率和精度。为了更好地阐述这些方法,表 3对各类方法的优缺点进行了详细介绍。
|
|
表 3 LP_MLFS、BR_MLFS、Direct_MLFS方法对比 Tab. 3 The comparison of LP_MLFS、BR_MLFS、Direct_MLFS |
考虑到多标记特征选择是否依赖于特定学习器,多标记特征选择算法可分为:过滤式(filter)、包裹式(wrapper)、嵌入式(embed)。
2.1 过滤式多标记特征选择过滤式多标记特征选择不依赖具体学习器,过滤式方法一般分为两类:第1类方法是选择合适的评价指标度量每个特征关于标记集的重要性,得出特征排序,根据预先设定的最小阈值或特征个数,选出对应特征子集;第2类方法是选择合适的评价指标,运用相应的搜索策略选出一个特征子集,无须预先设定最小阈值或特征个数。
第1类方法关键在于特征排序的好坏,且需要预先设定所选特征个数,这类方法常用评价标准主要有卡方、信息增益、互信息等。具体一些方法如下。
文献[23]基于信息增益提出了一种多标记特征选择方法,该方法首先计算每个特征和标记集之间的信息增益大小,以此度量每个特征的重要度;然后给定最小重要度阈值,进而选出特征子集。
文献[24]基于最大相关性最小冗余性(minimum redundancy maximum relevancy,mRMR)原则提出一种新的多标记特征选择方法,该方法运用互信息分别度量候选特征与标记集之间的相关性、候选特征与已选特征之间的冗余性,然后基于mRMR原则给出最终特征重要性度量。根据预先设定要选择的特征个数,运用所定义度量基于前向增量式搜索策略选出特征子集。该方法充分地考虑了特征之间的冗余性,剔除了更多的冗余特征。
文献[25]基于邻域互信息提出一种多标记过滤式特征选择方法,该方法从最大、平均、最小三个不同粒度的样本间隔定义了三种多标记邻域互信息,同样根据预先设定特征子集个数,选出合适的特征子集。相比于已有基于互信息的多标记特征选择方法,该方法最大优势在于处理数值型数据时无须进行离散化处理,避免了离散化所带来的信息损失。
第2类方法可直接选出特征子集,无须预先设定特征个数,这类方法主要基于粒计算理论,具体的特征评价标准有依赖度、邻域依赖度、模糊依赖度和辨识能力等,主要方法有互补属性约简、基于变精度粗糙集的多标记特征选择、基于邻域粗糙集的多标记特征选择、基于模糊粗糙集的多标记特征选择等。
文献[26]基于粗糙集理论构建了多标记可变精度属性约简方法,称为δ-置信度约简,它可以正确捕获标签间隐含的不确定性。此外,还引入了与δ-置信度约简相关的可分辨矩阵,基于可分辨矩阵来计算δ-置信度约简,进而得出多标记决策表的约简子集。该方法在理论和应用方面都具有重要意义。
文献[27]针对多标记分类任务,运用粗糙集理论系统分析了标记的不确定性,提出了保持标记不确定性不变的多标记特征选择方法。首先通过分析表明经典粗糙集中的依赖度并不能有效度量标记的不确定性;然后从标记不确定角度构建了多标记粗糙集模型,定义粗糙决策函数表示样本可能具有的标记集,细致决策函数表示样本确定具有的标记集,并结合这两种决策函数定义了特征的依赖度函数,提出了一种启发式多标记特征选择算法,即互补决策约简(complementary decision reduct, CDR)。CDR具有很强的理论保证,可以直接处理多标记数据,实验也展示了该方法的优越性。
文献[28]针对多标记分类任务,构建了多标记邻域粗糙集模型,给出新的下近似定义去刻画特征对于标记集的分类能力,设计了一种启发式多标记特征选择算法。算法基于邻域关系,因此可以直接对数值型多标记数据进行特征选择,而无须进行离散化。文中在5个数值型多标记数据上进行对比实验,验证了该算法的有效性。
文献[29]从标记关系出发对多标记数值型数据进行特征选择,首先定义了属性-标记矩阵概念;然后运用标记集上的模糊相似关系去刻画标记关系,给出了新的模糊上下近似、依赖度定义,并设计了一种前向启发式多标记特征选择算法。该方法将标记关系引入到多标记特征选择中,并从理论上分析了标记关系随属性集的粒度变化,实验验证了挖掘标记关系在多标记特征选择中的有效性。
文献[30]提出一种新的模糊粗糙集模型用于多标记特征选择。文中指出运用模糊粗糙集对多标记进行特征分析的瓶颈在于难以找到目标样本的真正异类样本,这直接影响模糊上下近似的鲁棒性。文中首先定义每个样本的得分向量,以评估相对于目标样本而言是异类样本的概率;然后利用局部采样来构造样本之间的稳健距离。文中定义了候选属性的重要度度量,并设计了一种贪心前向特征选择算法,实验验证了该算法的有效性。
文献[31]从样本和标记两个角度共同去刻画特征的区分能力。针对多标记特征选择任务,对模糊粗糙集框架下的模糊辨识关系重新定义,利用最大样本模糊辨识度量特征可区分的样本对个数,和最大标记模糊辨识度量特征可区分的样本对所对应的标记个数,引入调和系数将两种度量结合,设计了一种新的启发式多标记特征选择算法。文中从两个不同的角度度量特征的区分能力, 可以在保持或提高分类性能的基础上有效降低特征维度。
2.2 包裹式多标记特征选择包裹式多标记特征选择方法主要思想是从特征集合中选择可使学习器性能最佳的特征子集。由于特征子集组合种类随特征个数增加而指数性增长,因此从所有特征组合中进行搜索是一个NP-hard问题。为此一般会选取一些时间复杂度低的搜索策略,例如启发式策略或是演化算法等。
文献[32]提出了基于朴素贝叶斯的多标记分类(multi-label naive bayes classification, MLNB)算法。为了提高算法的效率,文中首先运用主成分分析法(principal component analysis, PCA)进行特征抽取,在降维后的数据上将MLNB作为包裹式分类器,排序损失RankLoss和汉明损失HammingLoss作为适应度函数,运用遗传算法搜索策略对多标记数据进行特征选择。
文献[33]首次将文化基因算法(memetic algorithm)应用到多标记特征选择方法中,统一了多标记特征选择与局部优化设计有关的特定问题,解决了关于染色体进行选择的局部优化问题。考虑到计算成本随特征和标记个数指数性增长,文中运用近似互信息降低增加操作(add operation,ADD)和删除操作(delete operation, DEL)的计算负担。相比于基于遗传算法的特征选择,该方法可有效防止过早收敛,并提高了计算效率。
文献[34]将多标记特征选择作为一种多目标优化问题,其目的是寻找一组帕累托非支配解。文中运用改进的多目标粒子群算法进行优化,采用概率编码运算符表示粒子,将汉明损失(HammingLoss)和特征数量作为算法的适应度函数。为保证粒子群优化(particle swarm optimization, PSO)算法能够收敛到帕累托前沿,采用自适应均匀变异来扩展所提算法的搜索能力;为提高算法的性能,文中也设计了一种基于差分学习的局部研究策略来探索搜索空间稀疏区域。
针对基于进化算法(evolutionary algorithm, EA)的多标记特征选择,文献[35]首次提出一种无参种群初始化方法,该方法可以作为进化算法的预处理。文中首先引入条件互信息,设计了一种得分函数计算每个特征的重要度,进而生成初始种群;然后将生成的种群作为基于EA的多标记特征选择方法的输入。该方法提高了传统基于EA的多标记选择方法的分类性能。
2.3 嵌入式多标记特征选择在嵌入式特征选择中,学习器训练与特征选择在同一个优化框架内完成,两者不可独立,一般嵌入式多标记特征选择式方法可分为两类:一类为基于树模型的特征选择方法,树节点的划分特征所组成的集合就是选择出的特征子集;另一类是在回归模型中引入惩罚项进行特征选择,基于不同的假设,一般的方法是使用l2, 1或l1范数对模型进行正则化。
文献[36]提出了基于树模型的多标记特征选择方法(multi-label C4.5, ML C4.5), 该方法中首先训练多标记分类树模型;然后基于树顶端特征分类能力强、树底端特征分类能力弱的原则,选择出合适的特征子集,该方法在训练分类模型的同时选出了合适的特征子集。
文献[37]提出了一种凸半监督多标记特征选择算法。文中首先将未标记数据的标记初始化为零,选用最小二乘损失函数和l2, 1正则项进行模型训练和稀疏特征选择;之后,将置信度高的未标记训练数据保存,并在下一轮迭代中将其视为已标记数据进行训练;最后,将获得的稀疏系数矩阵用于特征选择。该方法可以有效运用未标记数据进行特征选择,与现有的涉及特征分解的多标记特征选择算法不同,该算法只需要解决几个线性方程组。因此可应用于大规模多标记数据。
文献[38]提出了一种基于l2, 1范数正则化的多标记特征选择,该方法考虑了标记相关性,为避免原始标记空间噪音干扰,首先运用矩阵压缩的方法将原始标记空间压缩到一个低维空间;然后在压缩后的标记空间上构建回归模型,基于l2, 1范数行式稀疏的性质构建了一种嵌入式多标记特征选择。
文献[39]针对多标记学习提出一种基于流形正则化判别式特征选择(manifold regularized discriminative feature selection, MDFS)算法,MDFS结合流行假设,首先诱导出与原始特征空间具有相同局部结构的低维嵌入,引入线性映射函数去构建原始特征与低维嵌入之间的联系;考虑到标记之间的共现关系,MDFS引入标记流行正则化去捕获全局标记关系;最后引入l2, 1范数正则化实现特征选择。实验验证了MDFS具有较好的效果,引入标记相关性使MDFS的性能有了总体提高。
2.4 三种方法优缺点对比以上分别介绍了过滤式、包裹式、嵌入式的关键思想和代表方法,为更好地认识各类方法,表 4给出了各类方法优缺点的具体描述。
|
|
表 4 过滤式、包裹式和嵌入式方法对比 Tab. 4 The comparison of filter, wrapper and embedded |
多标记学习中每个标记具有不同的语义,因此每个标记可能对应不同的特征描述。针对多标记特征选择,从不同标记共享特征子集的程度,存在三种不同假设:1)所有标记共享相同特征子集;2)不同的标记享有不同的特征子集;3)将标记依据某种度量划分为多个标记粒,同一个粒内的标记享有相同的特征子集,不同粒内的标记享有不同特征子集。基于这三种不同假设,多标记特征选择算法可分为三类:标记共享式、标记专属式、标记粒化式。
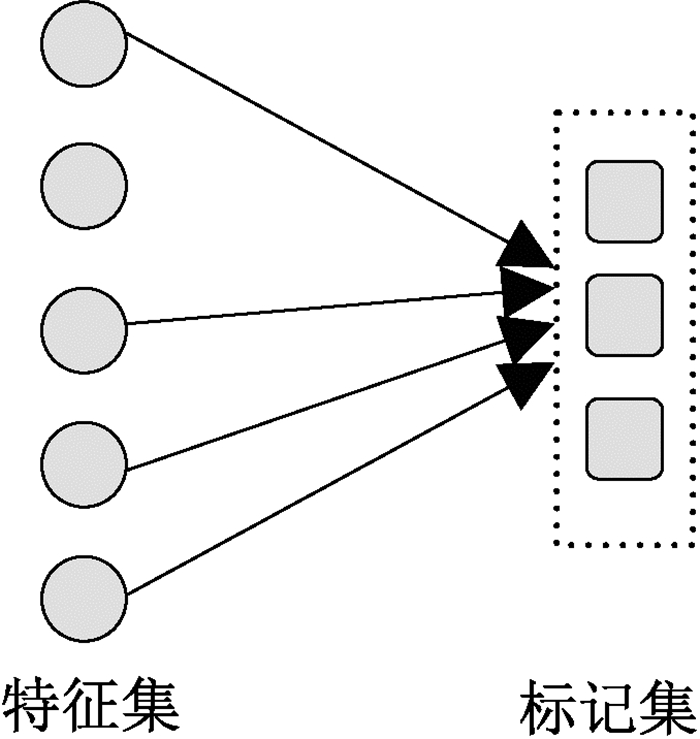
3.1 标记共享式标记共享式多标记特征选择方法,假设所有标记共享相同特征子集,图 1给出标记共享方法的直观示意。
|
图 1 共享式示意图 Fig. 1 The display of label-shared |
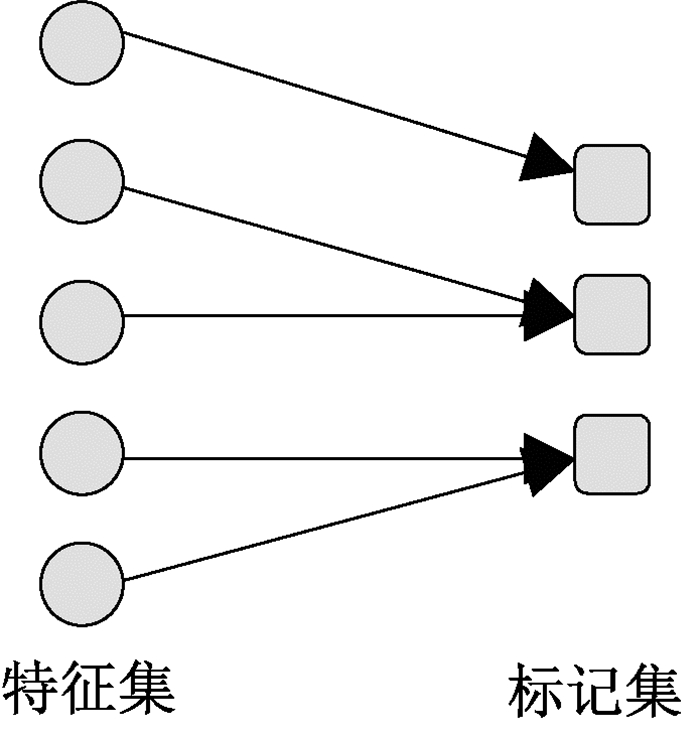
标记专属式多标记特征选择方法,考虑到每个标记应有不同刻画,对每个标记单独进行特征选择,选出每个标记专属特征子集,在图 2给出标记专属式方法的直观示意。
|
图 2 专属式示意图 Fig. 2 The display of label-specific |
文献[40]首次提出了标记专属特征的概念,认为每个标记具有其自身的特征,称这些特征为专属特征。文章提出了一种基于专属特征的多标记学习(multi-label learning with label specific features, LIFT)算法。LIFT首先对每个标记的正负类样本分别聚类,利用聚类结果分析得出每个标记的专属特征;然后利用专属特征对每个标记训练一个二分类模型。LIFT利用专属特征更好地刻画了每一个标记概念,取得了不错的分类效果。
LIFT专属特征的构建往往会增加特征维度,且在特征空间中存在大量冗余特征。为了解决这种问题,文献[41]提出一种基于模糊粗糙集的多标记专属特征选择(label-specific feature reduction with fuzzy rough set, FRS-LIFT)算法。同LIFT方法一样,该方法首先对每个标记构建其专属特征;然后,对每个标记的专属特征运用模糊粗糙集进行约简。为提高特征选择效率,文中也引入样本选择对数据进行压缩。与LIFT相比,该方法有效降低了特征维度,提高了算法效率,获得了不错的分类效果。
考虑到LIFT获得的专属特征不具有好的解释性或实际物理意义,且LIFT运用k-means聚类算法学习标记的专属特征,因此只能处理数值型多标记数据。文献[42]基于粗糙集理论提出一种新的专属特征学习算法(R-LIFT), R-LIFT运用正域约简获得每个标记的特征子集,将其作为标记的专属特征。R-LIFT基于粗糙集理论,无须引入参数,所获得的标记专属特征具有很好的解释性。
文献[43-44]提出一种嵌入式标记专属特征学习算法(learning label specific features, LLSF),并引入高阶标记相关性的改进算法(learning label specific features by learning class-dependent labels, LLSF-DL)。文中运用矩阵l1范数稀疏正则化进行特征选择,通过对稀疏向量之间内积进行约束和堆栈的方式引入二阶和高阶标记相关性,运用加速近端梯度法对模型进行优化。LLSF和LLSF-DL可以直接用于多标记分类,也可将所得到的特征作为一些二元相关分类方法的输入。
文献[45]在LLSF的基础上构建了一种新的嵌入式多标记专属特征选择算法(joint feature selection and classification for multilabel learning, JFSC),该方法同LLSF相同之处在于,都在回归框架下引入矩阵l1范数稀疏正则化学习标记专属特征,并在学习到的标记专属特征上构建多标记分类器。不同之处在于,JFSC结合判别分析的思想,引入Fisher判别式正则项去最大化类间方差和最小化类内方差,文中通过实验证明了利用标记相关性和学习标记专属特征对多标签学习的有效性。
文献[46]同时考虑标记相关性和标记专属特征,提出一种新的多标记学习方法。该方法通过增加额外特征引入标记相关性,运用矩阵l1范数稀疏正则化学习标记专属特征。标记关系和回归系数均作为未知变量,作为两个子问题交替优化,回归系数的优化是非光滑凸优化问题,文中采用近端梯度法。测试数据则先采用k最近邻(k-nearest neighbor, KNN)获得标记关系,再对其分类。
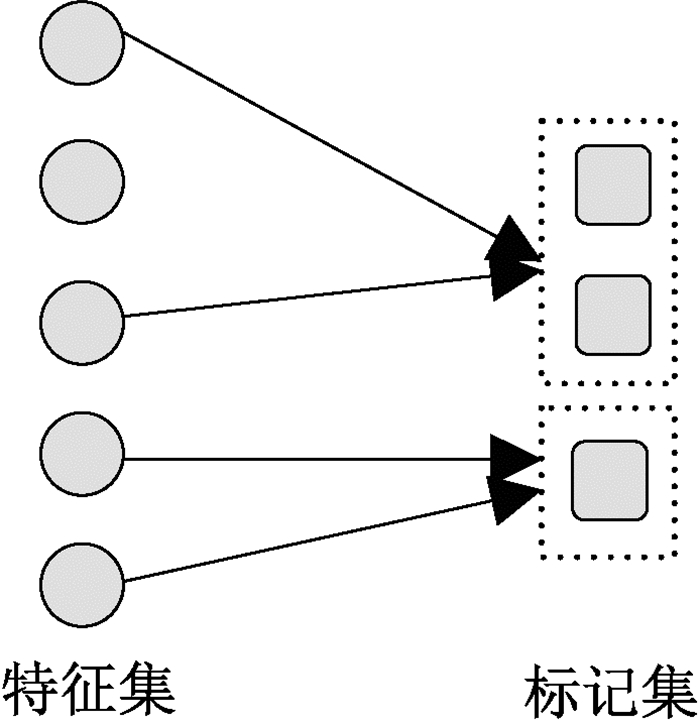
3.3 标记粒化式标记粒化式多标记特征选择方法,考虑了标记之间的相关性,相关性强的标记之间应该具有相同特征子集,反之相关性弱的标记应该具有不同特征子集,图 3给出了标记粒化式多标记特征选择算法的直观示意。
|
图 3 粒化式示意图 Fig. 3 The display of label-granulated |
文献[47]基于粒计算思想首次将标记粒化运用到多标记特征选择中,指出并非全部标记之间存在强的相关性,某个标记重要的特征可能反而会降低其他标记的分类性能,因此所有标记共享同一个特征子集不太合理;而标记的专属特征选择方法,在选择每个标记类属特征时并未考虑其他标记信息,并且处理大规模标记时,往往需要多次特征选择和训练多个学习器,效率低下。文献[47]为解决这两类方法所存在问题,提出了一种基于互信息的粒化多标记特征选择方法。算法分为三步:首先运用平衡聚类将标记集粒化到一系列标记粒,进而考虑了标记关系;然后对每个标记粒基于最大相关性最小冗余性原则进行特征选择;最后对每个标记粒利用所选特征子集训练分类模型。该方法首次将标记粒化的思想运用到多标记特征选择中,为多标记特征选择提供了一个新视角。
文献[48]提出一种新的多标记特征选择方法,基于粒计算理论,首先定义了一种基本元素用于刻画每个标记和特征的内在联系,根据标记之间基本元素集合的重叠程度,度量标记的相关性并计算对应判别矩阵,将相关性强的标记划分到同一个标记组,同时局部和全局标记关系被计算;然后对每个标记组分别进行特征选择;最后对每个标记组运用所选特征子集训练分类模型,该方法取得了不错的分类效果。
3.4 三种方法优缺点对比以上分别从标记的特征子集共享程度出发,分别介绍了标记共享式、标记粒化式、标记专属式三类多标记特征选择的核心思想和一些方法。为更好地认识各类方法的性质,表 5给出了各类方法优点和缺点的具体描述。
|
|
表 5 标记共享式、标记专属式、标记粒化式方法对比 Tab. 5 The comparison of label-shared, label-specific, label-granulated |
根据应用场景不同,多标记特征选择方法可分为静态式和增量式,下面将具体介绍这两类方法。
4.1 静态多标记特征选择本文前面所介绍的方法多为静态多标记特征选择方法,例如文献[24-25, 27-29],通常这类方法假设数据集直接全部给定,其样本、特征、特征值、标记不会随时间而发生改变。在数据集发生变化或更新时,这类方法通常需要重新对新数据进行特征选择,必然会存在很多冗余计算,浪费计算资源和时间。由于上面章节已经介绍了很多静态式方法,这部分不再对该类方法进行具体介绍。
4.2 增量式多标记特征选择在实际应用场景中,多标记数据的样本、特征、特征值、标记会随时间发生改变。对于更新后数据重新进行特征选择必然会存在冗余计算,怎样有效利用已获得的特征子集及引入动态更新机制已成为多标记特征选择的研究热点之一,目前已有一些相关方法被提出[49-55]。
流标记[49]:一般的多标记特征选择方法假设标记概念全部给定,但是现实领域中往往存在标记随着时间逐步加入的现象。例如图像标注领域,由于标注需求的改变可能会引入新的标注概念;社交网络中,热门话题标签每天也在不断变化。
文献[49]首次提出多标记流标记特征选择算法(multi-label feature selection with streaming labels, MLFSL),其思想是结合最大相关性最小冗余性原则和互信息度量获得每个新标记的特征排序列表;然后运用一个优化框架获得最终特征排序列表。无论是在标记空间固定还是在流标记实验设置下,MLFSL方法都取得了不错的效果。文献[50]基于类间区分和类内邻居识别策略提出一种新的多标记流标记特征选择(feature selection for multi-label learning with streaming label, FSSL)方法,该方法可以有效获得每个标记的专属特征,并定义一种新的融合策略获得最终的特征子集。相比静态多标记特征选择算法以及流标记特征选择算法,FSSL获得了更优越的性能,但是这些方法仍未将标记关系引入到特征选择中。
流特征[51]:一般的多标记特征选择方法假设特征全部给定,但是现实领域往往存在训练样本数保持不变而特征维度随时间逐步增加的现象,这种现象称为多标记流特征。大量现实应用领域存在流特征现象,如垃圾邮件过滤中,往往会设置敏感词库用于判断当前邮件是否为垃圾邮件,而敏感词库中的词汇会逐渐增加。传统的静态多标记特征选择算法已不能有效解决流特征问题。
文献[51]基于模糊互信息设计了特征完全已知或动态增加的多标记特征选择算法。文中首先给出样本在标记空间的相似性度量,以便计算特征和标记之间的模糊互信息。然后基于最大相关性最小冗余性原则,构建了一种特征空间完全已知的多标记特征选择算法。文中也构建了多标记流特征选择(multi-label streaming feature selection, MSFS)算法,MSFS具体分为两个主要步骤:在线相关性分析、在线冗余性分析。MSFS是首个多标记流特征选择方法,可以选择少量的特征来训练更强的模型。文献[52]基于邻域粗糙集模型提出一种多标记流特征选择算法。
文献[53]提出动态滑动窗口加权互信息流特征选择,首先引入互补概率定义了一种新的模糊信息熵;然后运用滑动窗口策略,分别设计了窗口大小固定和窗口大小自适应的多标记特征选择算法。文献[54]同时考虑流特征和标记分布问题,基于粗糙集理论提出一种新的多标记特征选择算法。
文献[55]提出一种在线多标记组特征选择(online multi-label group feature selection, OMGFS)算法,其面向特征随时间分组加入的场景由两阶段组成:在线组选择和在线组间选择。在线组选择主要判断新加入特征组是否应该添加到存储相关特征的缓冲池中。在线组间选择主要用于剔除缓冲池和已选特征中的冗余特征。OMGFS考虑了多标记问题中特征分组加入的场景,其对于多标记特征选择在动态环境下的研究具有重要意义。
5 进一步研究方向多标记特征选择可以有效解决多标记特征维度灾难,尽管已有大量多标记特征选择方法被提出,但仍然存在一些问题值得我们深入研究。
5.1 标记关系在多标记特征选择中的作用标记关系蕴含大量重要信息,已有许多研究将标记关系引入到多标记学习中,也有一些工作将标记关系引入到特征选择。即使有大量对于标记关系的研究,但是对于特征选择与标记关系的结合方式研究仍然很少,虽然有一些探索性工作,例如对标记空间粒化或分组[47-48],但是这些方法仍然存在粒度个数不确定等问题。因此怎样引入标记关系到多标记特征选择中仍然是一个挑战。
5.2 多标记特征选择的效率和搜索策略对于过滤式多标记特征选择方法,直接计算各个特征重要度得出特征排序,这种方法不能有效考虑特征之间的冗余性。即使运用贪心搜索策略可以在一定程度上考虑特征之间的冗余性,但这种方法需要多次对特征排序,时间复杂度很高,且得到的不一定是最优特征子集。包裹式多标记特征选择算法同样存在这种问题。因此,运用更高效的搜索策略,设计更快的多标记特征选择算法依旧是未来研究的重点。
5.3 弱监督问题下的多标记特征选择由于多标记数据标注概念多、标注代价大,人工标注往往会出现漏标或错标问题,称含有这种问题的学习为弱监督多标记学习。弱监督多标记学习近来已受到很多学者关注,其研究具有十分重要的意义。目前,对弱监督问题下的多标记特征选择研究工作仍然很少[56-57],弱监督问题下的多标记特征选择仍是未来一项重要研究课题。
5.4 多视图问题下的多标记特征选择多视图多标记学习是近来的研究热点之一[58],但是同一视图内不同特征之间以及不同视图不同特征之间必然存在冗余问题,从多个视图中选择合适的特征子集进行多标记分类,可有效提高分类的性能和效率。现有多标记特征选择方法不能直接处理多视图问题,因此多视图下的多标记特征选择仍值得深入研究。
6 总结本文对多标记特征选择方法进行总结,从4个角度对现有多标记特征选择方法进行归类,阐述各类方法的关键思想以及代表算法,并对每类方法进行客观概括,最后提出了若干有价值的方向。随着对多标记特征选择研究的不断深入,无论是效率、效果还是应用场景,一定会产生更多更好的研究成果。
| [1] |
BOUTELL M R, LUO J B, SHEN X P, et al. Learning multi-label scene classification[J]. Pattern recognition, 2004, 37(9): 1757-1771. DOI:10.1016/j.patcog.2004.03.009 (  0) 0) |
| [2] |
SCHAPIRE R E, SINGER Y. BoosTexter: a boosting-based system for text categorization[J]. Machine learning, 2000, 39(2): 135-168. (  0) 0) |
| [3] |
ZHANG M L, ZHOU Z H. Multilabel neural networks with applications to functional genomics and text categorization[J]. IEEE transactions on knowledge and data engineering, 2006, 18(10): 1338-1351. DOI:10.1109/TKDE.2006.162 (  0) 0) |
| [4] |
LIU H W, LI X L, ZHANG S C. Learning instance correlation functions for multilabel classification[J]. IEEE transactions on cybernetics, 2017, 47(2): 499-510. DOI:10.1109/TCYB.2016.2519683 (  0) 0) |
| [5] |
ZHANG Y, ZHOU Z H. Multilabel dimensionality reduction via dependence maximization[C]//The 23rd National Conference on Artificial Intelligence. Chicago, 2008: 1503-1505.
(  0) 0) |
| [6] |
NAULA P, AIROLA A, SALAKOSKI T, et al. Multi-label learning under feature extraction budgets[J]. Pattern recognition letters, 2014, 40(15): 56-65. (  0) 0) |
| [7] |
XU J H, LIU J L, YIN J, et al. A multi-label feature extraction algorithm via maximizing feature variance and feature-label dependence simultaneously[J]. Knowledge-based systems, 2016, 98: 172-184. DOI:10.1016/j.knosys.2016.01.032 (  0) 0) |
| [8] |
READ J, PFAHRINGER B, HOLMES G. Multi-label classification using ensembles of pruned sets[C]//IEEE International Conference on Data Mining. Pisa, 2008: 995-1000.
(  0) 0) |
| [9] |
READ J. A pruned problem transformation method for multi-label classification[C]//Proceedings of New Zealand Computer Science Research Student Conference. Christchurch, 2008: 143-150.
(  0) 0) |
| [10] |
TROHIDIS K, TSOUMAKAS G, KALLIRIS G, et al. Multi-label classification of music by emotion[J]. EURASIP journal on audio, speech, and music processing, 2011, 2011(1): 1-9. DOI:10.1186/1687-4722-2011-1 (  0) 0) |
| [11] |
DOQUIRE G, VERLEYSEN M. Feature selection for multi-label classification problems[C]//International Work-Conference on Artificial Neural Networks. Malaga, 2011: 9-16.
(  0) 0) |
| [12] |
REYES O, MORELL C, VENTURA S. Scalable extensions of the ReliefF algorithm for weighting and selecting features on the multi-label learning context[J]. Neurocomputing, 2015, 161: 168-182. DOI:10.1016/j.neucom.2015.02.045 (  0) 0) |
| [13] |
PEREIRA R B, PLASTINO A, ZADROZNY B C, et al. Categorizing feature selection methods for multi-label classification[J]. Artificial intelligence review, 2018, 49(1): 57-78. DOI:10.1007/s10462-016-9516-4 (  0) 0) |
| [14] |
TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Random k-labelsets for multilabel classification[J]. IEEE transactions on knowledge & data engineering, 2011, 23(7): 1079-1089. (  0) 0) |
| [15] |
SPOLAÔR N, CHERMAN E A, MONARD M C, et al. A comparison of multi-label feature selection methods using the problem transformation approach[J]. Electronic notes in theoretical computer science, 2013, 292: 135-151. DOI:10.1016/j.entcs.2013.02.010 (  0) 0) |
| [16] |
PUPO O, MORELL C, SOTO S V. ReliefF-ML: an extension of ReliefF algorithm to multi-label learning[C]//The 18th Iberoamerican Congress on Pattern Recognition. Havana, 2013: 528-535.
(  0) 0) |
| [17] |
SPOLAÔR N, CHERMAN E A, MONARD M C, et al. ReliefF for multi-label feature selection[C]//The Brazilian Conference on Intelligent Systems. Fortaleza, 2014: 19-24.
(  0) 0) |
| [18] |
LEE J, KIM D W. Feature selection for multi-label classification using multivariate mutual information[J]. Pattern recognition letters, 2013, 34(3): 349-357. DOI:10.1016/j.patrec.2012.10.005 (  0) 0) |
| [19] |
LEE J, KIM D W. Fast multi-label feature selection based on information-theoretic feature ranking[J]. Pattern recognition, 2015, 48(9): 2761-2771. DOI:10.1016/j.patcog.2015.04.009 (  0) 0) |
| [20] |
LEE J, KIM D W. Mutual information-based multi-label feature selection using interaction information[J]. Expert systems with applications, 2015, 42(4): 2013-2025. DOI:10.1016/j.eswa.2014.09.063 (  0) 0) |
| [21] |
LEE J, KIM D W. SCLS: multi-label feature selection based on scalable criterion for large label set[J]. Pattern recognition, 2017, 66: 342-352. DOI:10.1016/j.patcog.2017.01.014 (  0) 0) |
| [22] |
KASHEF S, NEZAMABADI-POUR H. A label-specific multi-label feature selection algorithm based on the Pareto dominance concept[J]. Pattern recognition, 2019, 88: 654-667. DOI:10.1016/j.patcog.2018.12.020 (  0) 0) |
| [23] |
LI L, LIU H W, MA Z J, et al. Multi-label feature selection via information gain[C]//International Conference on Advanced Data Mining and Applications. Guilin, 2014: 345-355.
(  0) 0) |
| [24] |
LIN Y J, HU Q H, LIU J H, et al. Multi-label feature selection based on max-dependency and min-redundancy[J]. Neurocomputing, 2015, 168: 92-103. DOI:10.1016/j.neucom.2015.06.010 (  0) 0) |
| [25] |
LIN Y J, HU Q H, LIU J H, et al. Multi-label feature selection based on neighborhood mutual information[J]. Applied soft computing, 2016, 38: 244-256. DOI:10.1016/j.asoc.2015.10.009 (  0) 0) |
| [26] |
LI H, LI D Y, ZHAI Y H, et al. A variable precision attribute reduction approach in multilabel decision tables[J]. The scientific world journal, 2014, 2014: 359626. (  0) 0) |
| [27] |
LI H, LI D Y, ZHAI Y H, et al. A novel attribute reduction approach for multi-label data based on rough set theory[J]. Information sciences, 2016, 367/368: 827-847. DOI:10.1016/j.ins.2016.07.008 (  0) 0) |
| [28] |
段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65. DUAN J, HU Q H, ZHANG L J, et al. Feature selection for multi-label classification based on neighborhood rough sets[J]. Journal of computer research and development, 2015, 52(1): 56-65. (  0) 0) |
| [29] |
郭荣超, 李德玉, 王素格. 基于标记关系的模糊粗糙集模型[J]. 模式识别与人工智能, 2017, 30(10): 952-960. GUO R C, LI D Y, WANG S G. Fuzzy rough set model based on label relations[J]. Pattern recognition and artificial intelligence, 2017, 30(10): 952-960. (  0) 0) |
| [30] |
LIN Y J, LI Y W, WANG C X, et al. Attribute reduction for multi-label learning with fuzzy rough set[J]. Knowledge-based systems, 2018, 152: 51-61. DOI:10.1016/j.knosys.2018.04.004 (  0) 0) |
| [31] |
姚二亮, 李德玉, 李艳红, 等. 基于双空间模糊辨识关系的多标记特征选择[J]. 模式识别与人工智能, 2019, 32(8): 709-717. YAO E L, LI D Y, LI Y H, et al. Multi-label feature selection based on fuzzy discernibility relations in double spaces[J]. Pattern recognition and artificial intelligence, 2019, 32(8): 709-717. (  0) 0) |
| [32] |
ZHANG M L, PEÑA J M, ROBLES V. Feature selection for multi-label naive Bayes classification[J]. Information sciences, 2009, 179(19): 3218-3229. DOI:10.1016/j.ins.2009.06.010 (  0) 0) |
| [33] |
LEE J, KIM D W. Memetic feature selection algorithm for multi-label classification[J]. Information sciences, 2015, 293: 80-96. DOI:10.1016/j.ins.2014.09.020 (  0) 0) |
| [34] |
ZHANG Y, GONG D W, SUN X Y, et al. A PSO-based multi-objective multi-label feature selection method in classification[J]. Scientific reports, 2017, 7(1): 376. DOI:10.1038/s41598-017-00416-0 (  0) 0) |
| [35] |
LIM H, KIM D W. MFC: initialization method for multi-label feature selection based on conditional mutual information[J]. Neurocomputing, 2020, 382: 40-51. DOI:10.1016/j.neucom.2019.11.071 (  0) 0) |
| [36] |
CLARE A, KING R D. Knowledge discovery in multi-label phenotype data[C]//Proceedings of the 5th European Conference on Principles of Data Mining and Knowledge Discovery. Freiburg, 2001: 42-53.
(  0) 0) |
| [37] |
CHANG X J, NIE F P, YANG Y, et al. A convex formulation for semi-supervised multi-label feature selection[C]//The Twenty-eighth AAAI Conference on Artificial Intelligence. Canada, 2014: 1171-1177.
(  0) 0) |
| [38] |
JIAN L, LI J D, SHU K, et al. Multi-label informed feature selection[C]//The Twenty-fifth International Joint Conference on Artificial Intelligence. New York, 2016: 1627-1633.
(  0) 0) |
| [39] |
ZHANG J, LUO Z M, LI C D, et al. Manifold regularized discriminative feature selection for multi-label learning[J]. Pattern recognition, 2019, 95: 136-150. DOI:10.1016/j.patcog.2019.06.003 (  0) 0) |
| [40] |
ZHANG M L, WU L. LIFT: Multi-label learning with label-specific features[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 37(1): 107-120. (  0) 0) |
| [41] |
XU S P, YANG X B, YU H L, et al. Multi-label learning with label-specific feature reduction[J]. Knowledge-based systems, 2016, 104: 52-61. DOI:10.1016/j.knosys.2016.04.012 (  0) 0) |
| [42] |
李华, 李德玉, 王素格, 等. 基于粗糙集的多标记专属特征学习算法[J]. 小型微型计算机系统, 2015, 36(12): 2730-2734. LI H, LI D Y, WANG S G, et al. Multi-label learning with label-specific features based on rough sets[J]. Journal of Chinese computer systems, 2015, 36(12): 2730-2734. (  0) 0) |
| [43] |
HUANG J, LI G R, HUANG Q M, et al. Learning label specific features for multi-label classification[C]//IEEE International Conference on Data Mining. Atlantic City, 2015: 181-190.
(  0) 0) |
| [44] |
HUANG J, LI G R, HUANG Q M, et al. Learning label-specific features and class-dependent labels for multi-label classification[J]. IEEE transactions on knowledge and data engineering, 2016, 28(12): 3309-3323. DOI:10.1109/TKDE.2016.2608339 (  0) 0) |
| [45] |
HUANG J, LI G R, HUANG Q M, et al. Joint feature selection and classification for multilabel learning[J]. IEEE transactions on cybernetics, 2018, 48(3): 876-889. DOI:10.1109/TCYB.2017.2663838 (  0) 0) |
| [46] |
ZHANG J, LI C D, CAO D L, et al. Multi-label learning with label-specific features by resolving label correlations[J]. Knowledge based systems, 2018, 159: 148-157. DOI:10.1016/j.knosys.2018.07.003 (  0) 0) |
| [47] |
LI F, MIAO D Q, PEDRYCZ W. Granular multi-label feature selection based on mutual information[J]. Pattern recognition, 2017, 67: 410-423. DOI:10.1016/j.patcog.2017.02.025 (  0) 0) |
| [48] |
CHE X Y, CHEN D G, MI J S. A novel approach for learning label correlation with application to feature selection of multi-label data[J]. Information sciences, 2020, 512: 795-812. DOI:10.1016/j.ins.2019.10.022 (  0) 0) |
| [49] |
LIN Y J, HU Q H, ZHANG J, et al. Multi-label feature selection with streaming labels[J]. Information sciences, 2016, 372: 256-275. DOI:10.1016/j.ins.2016.08.039 (  0) 0) |
| [50] |
LIU J H, LI Y W, WENG W, et al. Feature selection for multi-label learning with streaming label[J]. Neurocomputing, 2020, 387: 268-278. DOI:10.1016/j.neucom.2020.01.005 (  0) 0) |
| [51] |
LIN Y J, HU Q H, LIU J H, et al. Streaming feature selection for multi label learning based on fuzzy mutual information[J]. IEEE transactions on fuzzy systems, 2017, 25(6): 1491-1507. DOI:10.1109/TFUZZ.2017.2735947 (  0) 0) |
| [52] |
LIU J H, LIN Y J, LI Y W, et al. Online multi-label streaming feature selection based on neighborhood rough set[J]. Pattern recognition, 2018, 84: 273-287. DOI:10.1016/j.patcog.2018.07.021 (  0) 0) |
| [53] |
程玉胜, 李雨, 王一宾, 等. 动态滑动窗口加权互信息流特征选择[J]. 南京大学学报(自然科学版), 2018, 54(5): 974-985. CHENG Y S, LI Y, WANG Y B, et al. Streaming feature selection with weighted fuzzy mutual information based on dynamic sliding window[J]. Journal of Nanjing university (natural science), 2018, 54(5): 974-985. (  0) 0) |
| [54] |
程玉胜, 陈飞, 王一宾. 基于粗糙集的数据流多标记分布特征选择[J]. 计算机应用, 2018, 38(11): 3105-3111. CHENG Y S, CHEN F, WANG Y B. Feature selection for multi-label distribution learning with streaming data based on rough set[J]. Journal of computer applications, 2018, 38(11): 3105-3111. (  0) 0) |
| [55] |
LIU J H, LIN Y J, WU S X, et al. Online multi-label group feature selection[J]. Knowledge-based systems, 2018, 143: 42-57. DOI:10.1016/j.knosys.2017.12.008 (  0) 0) |
| [56] |
ZHU P F, XU Q, HU Q H, et al. Multi-label feature selection with missing labels[J]. Pattern recognition, 2018, 74: 488-502. DOI:10.1016/j.patcog.2017.09.036 (  0) 0) |
| [57] |
HUANG J, QIN F, ZHENG X, et al. Improving multi-label classification with missing labels by learning label-specific features[J]. Information science, 2019, 492: 124-146. DOI:10.1016/j.ins.2019.04.021 (  0) 0) |
| [58] |
ZHU C M, MIAO D Q, WANG Z, et al. Global and local multi-view multi-label learning[J]. Neurocompution, 2020, 371: 67-77. DOI:10.1016/j.neucom.2019.09.009 (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


