0 引言

伴随着网络用户个人信息泄露、各大数据库信息外泄、关键信息服务器设备受威胁及用户主机被入侵等事件的频繁发生, 网络安全问题已经成为当今社会的热点议题之一。由于网络入侵行为方式的不断多样化和复杂化, 基于防火墙等的静态安全防范技术已无法满足当代网络安全需求, 主动防御网络异常入侵行为的安全防护技术——入侵检测系统应运而生^[1]。

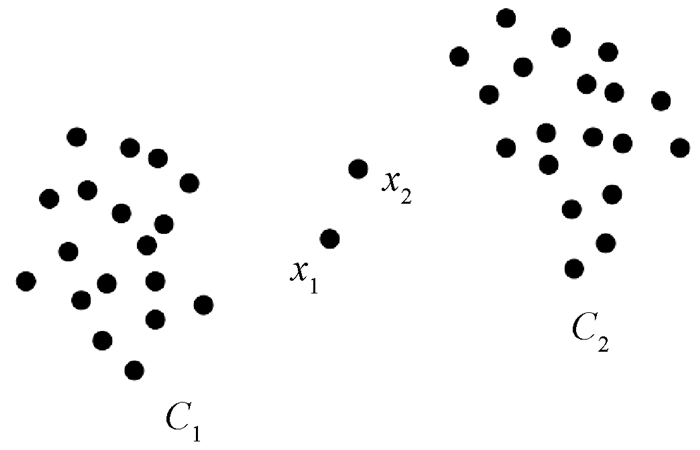
K-means算法是一种应用广泛的硬聚类方法, 采用距离作为相似性评价指标, 即认为两个数据对象之间的距离越近, 相似度越大。该算法在人工给定k值的前提下, 通过迭代满足平方误差准则函数收敛, 输出聚类结果。一些研究者针对传统K-means算法提出了一系列改进算法^[2-7]。文献[5]提出了基于免疫规划的K-means聚类算法, 该算法有效克服了传统K-means聚类算法易陷入局部极小值的缺点, 而且有效地避免了对初始化选值敏感性的问题。文献[6]基于指数函数性质、权重调节、偏执项和手肘法基本思想, 提出了改进的ET-SSE算法, 使得k值预测准确率和预测结果更加稳定。目前大多数聚类方法都是基于二支决策思想, 即判定某个数据对象属于某个类簇, 或不属于某个类簇, 在处理一些网络数据集时, 传统的二支聚类方法仍存在一定的不足。一方面, 聚类结果并不能完全反映所有数据对象本身的性质特征。例如在图 1中, 按照传统二支聚类方法, 数据对象x₁、x₂分别归到C₁和C₂两个簇中, 但实际上数据点x₁、x₂与对应簇中数据对象存在明显差异, 所以采取硬聚类方法必会降低入侵检测率, 增大误检率。另一方面, 传统K-means聚类算法采用固定的k值, 但是在现实网络环境中很难提前预测所有数据行为的准确类别数, 所以固定的k在一定程度上影响对网络数据的分类和判定。

为克服上述两方面的不足, 本文将结合三支决策思想, 提出基于三支动态阈值K-means聚类的入侵检测算法。该算法通过设定阈值α, 可以实现对k值的动态调整, 利用数据对象的q邻域实现对不确定性数据的延迟决策, 进而提高入侵检测系统的检测率, 降低误检率。

1 入侵检测系统与K-means聚类算法 1.1 入侵检测系统

入侵检测系统能实时监控、检测网络系统和数据资源, 迅速发现非法攻击网络系统、非法操作数据资源的入侵行为, 同时还能提前阻止合法用户对系统的误操作, 维护网络系统安全。通常情况下, 入侵检测系统由数据采集、数据分析以及响应处理三大部分构成^[8]。

传统的入侵检测系统以误用检测技术为主, 建立已知入侵行为特征数据库, 利用该数据库对网络中的数据流量和活动行为进行实时监控, 以模式匹配的方式判断网络行为及其变种行为是否异常, 当数据特征与特征数据库中的任何一条规则有交集, 即可判定为入侵行为。K-means聚类算法作为典型二支聚类算法在入侵检测过程中的应用主要表现在两个阶段:第一阶段, 数据分析并构建分类器; 第二阶段, 检测引擎通过分类器判别每个数据对象的行为特征^[9]。

1.2 K-means聚类算法

K-means聚类算法以数据对象间的欧氏距离作为衡量数据对象间联系是否紧密的依据, 认为特征属性越接近的数据对象之间距离越小^[10]。K-means聚类算法遵循聚类的两点假设:(1)在整个测试数据集中正常数据对象在数量上远远大于非正常数据对象; (2)正常数据对象与非正常数据对象之间存在明显的差异性。

K-means聚类算法流程如下。

输入:包含n个数据对象的数据集X={x₁, x₂, …, x_n}和聚类个数k;

输出:k个聚类簇。

(1) 在数据集X={x₁, x₂, …, x_n}中随机选取k个数据对象, 构成所属簇的第一次聚类中心点集U={u₁, u₂, …, u_k}。

(2) 计算数据集X中所有数据点x_i到k个聚类中心点u_j的欧氏距离d(x_i, u_j), 并将它们归到距离最近的簇C_j={x_i|d(x_i, u_j)≤d(x_i, u_l), j≠l}中。

(3) 重新计算每个簇中所有数据对象的新均值${u_j} = \frac{1}{{\left| {{C_j}} \right|}}\sum\limits_{{x_i} \in {C_j}} {{x_i}} $, 作为簇的新的聚类中心点。

(4) 计算目标函数$J = \sum\limits_{j = 1}^k {\sum\limits_{{x_i} \in {C_j}} d } {\left( {{x_i}, {u_j}} \right)^2}$, 如果J收敛, 输出聚类结果。否则, 继续执行步骤(2)和(3), 直到收敛为止。

2 三支聚类思想

为了解决传统聚类算法在入侵检测系统应用中存在的问题, 很多学者对二支聚类算法进行了改进, 将三支决策思想引入聚类算法, 提出三支聚类方法。三支决策理论最早由Yao在决策粗糙集的基础上提出^[11-12], 其核心思想是将待决策项拓展为正域决策、负域决策和边界域决策。有充分把握、了解全面的事物, 直接给出接受或者拒绝的判断, 否则做进一步调查, 表现为延迟决策^[13]。近年来, 在不确定性信息处理方面, 三支决策理论得到了广泛推广^[14-18]。文献[14]提出了基于不完备信息系统的三支决策模型。文献[17]将三支决策思想引入聚类分析中, 提出了一种自动三支决策聚类算法, 该方法为自动确定K-means算法聚类数目提供了一种新的解决思路。文献[19]借数据对象的q领域, 把二支聚类结果中不确定性数据进行分离, 每一类数据均由确定性数据组成的核心区域(core)和不确定性数据组成的边界区域(fringe)共同构成。

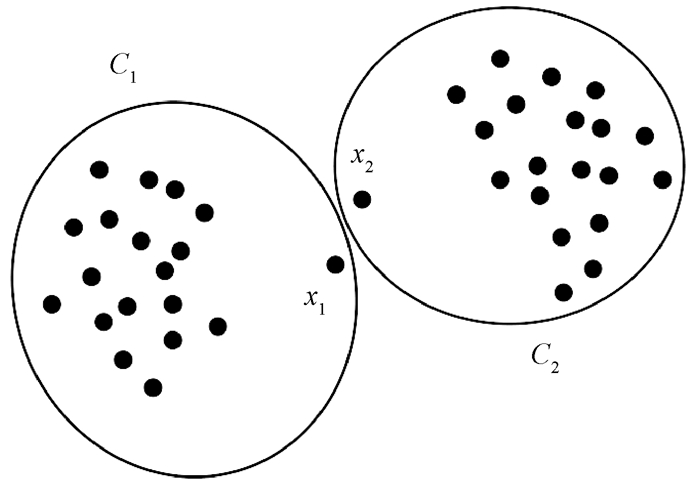
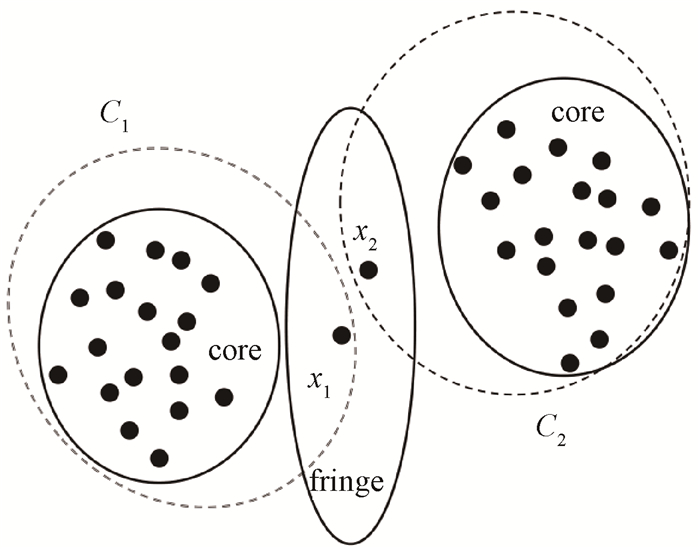
以图 1为例, 利用传统硬聚类方法, 数据对象x₁和x₂只能分别归属到类C₁和C₂, 但x₁和x₂与类C₁和C₂中的数据对象又有显著差异, 聚类结果如图 2所示。而利用三支聚类方法进行聚类, 结果如图 3所示。x₁和x₂分别被划分到C₁和C₂的边界区域内, 可作为不确定性数据待进一步处理。与传统硬聚类方法相比, 该种聚类方法在结构上有明显的优势, 可以针对离群数据点的特殊性, 对其做进一步聚类。

三支聚类方法是对传统二支聚类方法的推广, 是为解决对不确定性数据对象进行合理归类这一问题而提出的一种解决方案。当数据对象难以立刻判断其所属类别时, 可将其归至边界区域, 对于能够准确判定类别的数据对象可归至核心区域。对于数据集X={x₁, x₂, …, x_n}, 假设C={C₁, C₂, …, C_k}是利用二支聚类方法对X进行聚类的结果。结合三支决策思想, 对每个类别C_i进行改进, 用C_i^P, C_i^B两个集合表示一个类C_i=C_i^P∪C_i^B, 满足:(1) $C_i^P \ne \emptyset , i = 1, 2, \cdots , k;(2)\;\mathop {\mathop {\rm{U}}\limits^k }\limits_{i = 1} \left( {C_i^P \cup C_i^B} \right) = X$。其中, 集合C_i^P, C_i^B分别称为类的核心区域和边界区域。核心区域中的数据对象确定属于某个类C_i, 边界区域中的数据对象可能属于类C_i。

在入侵检测过程中, 将核心区域数据直接判断为入侵数据或正常数据, 将边界区域数据进行延迟决策, 以减少误判。

3 基于三支动态阈值K-means聚类算法

通常情况下, 在入侵检测系统中同一类行为数据普遍具有较高的相似性^[20], 所以基于三支聚类算法的结果集中在绝大多数边界区域C_i^B, 基本可以判定为是与该类核心区域C_i^P非同类的行为数据。在基于q邻域三支聚类算法的基础上, 为消除人工干预k值对K-means算法聚类效果的影响, 本文提出以下基于三支动态阈值K-means聚类算法。

在K-means聚类过程中引入一个距离阈值α, 利用硬聚类算法对其进行预测, 并在算法执行过程中动态优化。K-means算法采用距离作为相似性的评价指标, 引入距离阈值α可以有效地将离群数据对象单独成簇, 并将其作为新的聚类中心参与数据训练。聚类中心的动态调整在一定程度上消除了人工干预k值对K-means算法聚类效果的影响。基于三支动态阈值K-means聚类算法流程如下。

输入:包含n个数据对象的数据样本集X={x₁, x₂, …, x_n}, 聚类个数为k, 邻域为q, 阈值为α;

输出:聚类结果集C。

(1) 在数据集X={x₁, x₂, …, x_n}中随机选取k个数据对象, 构成初始聚类中心点集U={u₁, u₂, …, u_k}。

(2) 计算数据集中所有剩余数据对象{x_i|x_i∉U}到每个聚类中心u_j的距离d(x_i, u_j), 并把它们归到距离最近的簇C_j={x_i|d(x_i, u_j)≤d(x_i, u_l), j≠l}中。

(3) 由函数$\alpha = \frac{1}{k}\sum\limits_{j = 1}^k {\left( {\frac{1}{{\left| {{C_j}} \right|}}\sum\limits_i d \left( {{x_i}, {u_j}} \right)} \right)} $得出距离阈值α的预测值, 即初始阈值。

(4) 遍历数据集X={x₁, x₂, …, x_n}中所有数据点{x_i|x_i∉U|}, 当∃d(x_i, u_j)＜α时, 将x_i归到距离最近的簇C′_j={x_i|d(x_i, u_j)≤d(x_i, u_l), j≠l}中; 当∀d(x_i, u_j)≥α时, 令u_k+1= x_i, 更新中心点集U={u₁, u₂, …, u_k+1}, 即将x_i作为数据集X中单独存在的簇, 初始聚类中心为x_i, 簇的数量更新为k′。

(5) 重新计算每个簇中所有数据对象的新均值$u_j^\prime = \frac{1}{{\left| {C_j^\prime } \right|}}\sum\limits_{{x_i} \in C_j^\prime } {{x_i}} $, 作为簇的新的聚类中心点。

(6) 继续执行步骤(3)~(5), 依据目标函数的值$J = \sum\limits_{j = 1}^{{k^\prime }} {\sum\limits_{{x_i} \in C_j^\prime } d } {\left( {{x_i}, u_j^\prime } \right)^2}$, 设置最大迭代次数, 避免陷入无限循环, 最终输出二支聚类结果集C′={C′₁, C′₂, …, C′_k′}。

(7) 取所有类样本数量均值的$\frac{1}{{10}}$作为邻域大小, 由函数$q = \frac{1}{{10{k^\prime }}}\sum\limits_{j = 1}^{{k^\prime }} {\left| {C_j^\prime } \right|} $得出q的预测值。

(8) 遍历二支聚类结果集C′={C′₁, C′₂, …, C′_k′}中所有类C′_j, 任取x_i∉C′_j, 考虑x_i的q邻域Neig_q(x_i)(距离该数据点最近的q个数据点组成的集合), 若Neig_q(x_i)∩C′_j≠$\emptyset$, 则x_i∈C^B′_j;

(9) 对每一类C′_j, 取x_i∈C′_j, 考虑x_i的q邻域Neig_q(x_i), 若Neig_q(x_i)⊆C′_i, 则x_i∈C^P′_j, 否则x_i∈C^B′_j;

(10) 通过步骤(8)和(9)得到C^P′_j和C^B′_j(j=1, 2, …, k′), 返回C″={(C^P′₁, C^B′₁), (C^P′₂, C^B′₂), …, (C^P′_k′, C^B′_k′)}, 令C_P={C^P′₁, C^P′₂, …, C^P′_k′}。

(11) 令X=C^B′₁∪C^B′₂∪…∪C^B′_k′, 执行步骤(1)~(6), 得到对边界区域数据对象的二次聚类结果集C′={C′₁, C′₂, …, C′_k′}, 令C_B=C′。

(12) 输出最终聚类结果集C={C_B, C_P}。

最终聚类结果集由C_B和C_P两部分构成, 结果集C_P中包含所有经过确定性划分的核心区域数据对象, C_B中包含被划分至不确定性边界区域后, 经二次确定性划分处理的数据对象, 由此得出的聚类结果集在准确率上明显高于传统二支聚类算法。

4 实验与结果分析 4.1 测试数据集的预处理

文中采用网络入侵检测算法的常用测试数据集KDD Cup99(http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html)进行实验。该数据集是从一个模拟的美国空军局域网上采集来的9个星期的网络连接数据, 包含具有标识的训练数据集kddcup_corrected和未加标识的测试数据集kddcup_testdata。训练数据集和测试数据集有着不同的概率分布, 测试数据集中包含了一些未出现在训练数据集中的攻击类型, 使得入侵检测更具有现实性。此次实验使用数据包kddcup_data_10percent验证基于三支动态阈值K-means聚类算法在性能上优于传统K-means算法。kddcup_data_10percent数据包是对KDD Cup99数据集(约500万条数据记录)10%的抽样。

kddcup_data_10percent数据包中每条数据记录为

0、tcp、http、SF、297、13787、0、0、0、0、0、1、0、0、0、0、0、0、0、0、0、0、2、2、0.00、0.00、0.00、0.00、1.00、0.00、0.00、177、255、1.00、0.00、0.01、0.01、0.00、0.00、0.00、0.00、normal。

0、udp、private、SF、105、147、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、2、2、0.00、0.00、0.00、0.00、1.00、0.00、0.00、255、254、1.00、0.01、0.00、0.00、0.00、0.00、0.00、0.00、snmpgetattack。

kddcup_data_10percent数据包中的每一条数据记录包含了41个固定的特征属性和1个类标识, 类标识用来标记该条数据记录是正常的或是某种具体类型的攻击行为。每条数据记录中包含连接持续时间、协议类型、目标主机的网络服务类型、访问控制文件的次数等属性。在41个固定的特征属性中, 9个为离散(symbolic)型, 32个为连续(continuous)型。

K-means聚类算法中使用计算距离的方法对数据进行聚类, 对于字符型特征属性首先需要数值化。对于连续型特征属性, 各属性的度量方法不一样, 一般而言, 变量所用的度量单位越小, 可能的值域就越大, 这样对聚类结果的影响也越大, 即在计算数据间距离时对聚类的影响越大, 甚至会出现“大数”吃“小数”的现象。因此为消除由于属性度量的差异对聚类产生的影响, 需要对特征属性进行标准化处理:${x_i} = \frac{{{X_i} - Min}}{{Max - Min}}$

4.2 实验结果及分析

本算法是在windows 10系统下的Python 3.7.2 64-bit环境下引入sklearn、numpy、csv等实现的。

kddcup_data_10percent数据包中的约30万条数据记录包含约85%正常行为数据、15%入侵行为数据(21类)。入侵检测算法采用两个性能指标进行评价^[21], 这两个指标定义为

$ 检测率(DR) = \frac{{检测到的入侵数据}}{{入侵数据总数}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;误检率(\mathit{F}R) = \frac{{误报为入侵的正常数据}}{{正常数据总数}}。$

实验一:在kddcup_data_10percent数据包中依次随机选取含有20 000条正常数据和2 000条攻击数据(含21类攻击行为)的五个数据集D₁、D₂、D₃、D₄、D₅, 作为本次实验的测试数据集。实验结果如表 1所示。

实验二:分别选取如表 2所示的五个数据集H₁、H₂、H₃、H₄、H₅作为本次实验的测试数据集。

实验一通过随机抽取方式选用性质相同的D₁、D₂、D₃、D₄、D₅五个测试数据集进行横向对比, 发现基于三支动态阈值K-means聚类算法无论从检测率还是误检率上都优于传统的K-means聚类算法。

实验二通过选用包含不同数量攻击类型的测试数据集H₁、H₂、H₃、H₄、H₅进行纵向对比, 实验结果表明当测试数据集中攻击类型逐渐增多时, 基于三支动态阈值K-means聚类算法与传统K-means算法相比, 误检率显著降低, 如表 3所示。

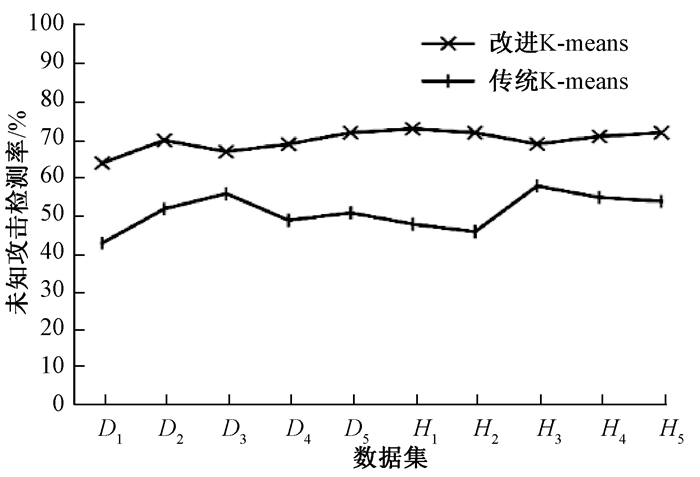
图 4为改进前后K-means算法针对测试数据集中未知攻击类型数据多次实验的结果对比图, 表明基于三支动态阈值K-means聚类算法具有更好的检测未知攻击类型的性能。

5 总结与展望

本文受三支决策思想和三支聚类方法的启发, 针对网络访问数据的复杂性与不确定性特点, 提出了基于三支动态阈值K-means聚类的入侵检测算法。通过设定距离阈值α实现对聚类个数k的动态优化, 同时利用数据对象的q邻域与初次聚类中簇的关系, 分离出不确定性网络访问数据并置于边界区域, 然后对该区域数据再次聚类并做出检测判断。采用这种对不确定性数据延迟决策的方法, 可以降低入侵检测过程中的误判带来的风险。通过一系列对比实验, 发现该算法较传统二支聚类K-means算法, 其检测率的提高和误检率的降低都是显著的, 验证了本文算法的有效性。同时, 在实验过程中我们还发现, 把正常数据误报为入侵数据或把入侵数据误报为正常数据, 两者给受保护系统带来的风险显然是不一样的, 后者会远远大于前者。在保证系统具有较高检测率和较低误检率的前提下, 如何进一步降低入侵数据误报为正常数据带来的风险, 最大程度上维护系统的安全是今后继续研究的方向。