2. 宁夏智能信息与大数据处理重点实验室 宁夏 银川 750021
2. Ningxia Key Laboratory of Intelligent Information and Big Data Processing, Yinchuan 750021, China
0-1背包问题(0-1 knapsack problem,0-1 KP)是运筹学中一类重要的组合优化问题,同时也是一类NP难问题,旨在寻求满足背包约束条件下具有最大价值的物品装载方案[1-2]。现实世界中很多复杂问题通过编码都可以转换为背包问题,如工业、经济、金融等方面的资源配置、资金预算、公钥密码系统构建以及装载问题等[3]。0-1背包问题的求解过程本质上为:在不超出背包可装载极限的条件下,选取那些装包比不装包更能使背包获得最大价值的物体。目前求解0-1背包问题的算法很多,除精确算法如回溯法、分支限界法等以外,还有可快速近似求解背包问题的演化算法(evolutionary algorithm,EA)、启发式遗传算法(genetic algorithm,GA)、蚁群优化算法(ant colony optimization, ACO)以及粒子群优化算法(particle swarm optimization,PSO)等[4-7]。但当问题规模较大时,精确算法的求解复杂度是指数函数,而启发式算法求解精确度低。置信传播(belief propagation,BP)算法是一种有效求解组合优化问题的近似算法,可计算边际概率,被广泛应用于人工智能和工程技术的各个方面[8-9]。分析BP算法的原理可以发现,其特征是基于因子图模型的一种消息循环更新算法,该消息可以理解为图上相连两节点之间的一种以概率表示的约束关系。通过某种迭代策略对因子图边上的信息进行传播计算,所有传入节点的信息共同决定该节点传出的信息。信息迭代过程可能收敛到某一组固定点,或可能无限次进行迭代(不收敛)。如果BP算法收敛,则产生一组稳定的边际分布,可以确定部分变量的取值。当求解的问题可用树状因子图表示时,BP算法将退化为一种与动态规划算法相似的优化方法,在图模型上沿着边传递更新变量节点之间的消息,从而得到优化和推理的正确解。
基于上述研究发现,0-1背包问题的可行解由一组高概率装包的物体组成,而BP算法可根据变量的边际概率确定变量取值。因此,本文提出一种求解0-1背包问题的BP算法。首先确定0-1背包问题的线性规划,将线性规划的约束条件转化为因子图的子句节点,设计出0-1背包问题的因子图模型;然后采用指数函数的形式,根据每个物体项的价值设置因子图的初始概率;最后利用BP算法的信息迭代方程在因子图上计算求解。
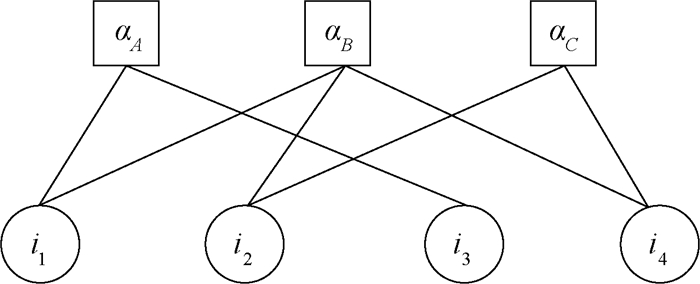
1 基本知识 1.1 图模型因子图是将一个具有多变量的全局函数因子分解为几个局部函数的乘积而得到的一种双向图模型[10-12]。这种图模型可以为信息传播算法的使用提供建模基础,简化概率分布的边缘化计算,以概率判断并确定变量取值。因子图包含两种节点:变量节点和子句节点[13]。变量节点代表联合概率分布函数的所有自变量,子句节点代表因式分解得到的多个局部函数。每个子句节点相连的变量节点都是对应的局部函数辖域内的自变量,每个变量节点相连的子句节点都是包含该变量的局部函数节点。对于f(i1, i2, i3, i4)=αA(i1, i3)αB(i1, i2, i4)αC(i2, i4),函数f和变量i之间的关系如图 1所示。
|
图 1 因子图实例 Fig. 1 Example of factor graph |
BP算法以因子图模型为传播载体,在因子图的每条边(i, α)上定义两种信息,分别为变量发送给约束的信息μi→α(di)和约束发送给变量的信息ηα→i(di)[14-15]。其中μi→α(di)表示在假设没有约束α的条件下,变量i取值为di的概率;ηα→i(di)表示约束α要求变量i取值为di的概率[16-17]。则可得BP算法的迭代方程为
| $ \mu _{i \to \alpha }^{t + 1}({d_i}) = {Z_{i \to \alpha }}\prod\limits_{b \in V\left( i \right)\backslash \alpha } {\eta _{b \to i}^t} ({d_i}),$ | (1) |
| $ \eta _{\alpha \to i}^{t + 1}({d_i}) = {Z_{\alpha \to i}}\sum\limits_{j \in V\left( \alpha \right)\backslash i} S (X_0^{^\alpha })\prod\limits_{j \in V\left( \alpha \right)\backslash i} {\mu _{j \to \alpha }^t} ({d_j}),$ | (2) |
式中:V(i)表示所有与i相连的约束集合,V(i)\α表示从V(i)中除去α;V(α)表示子句α包含的所有变量集合,V(α)\i表示从V(α)中除去i;Zi→α和Zα→i为归一化因子;S(X0α)为标识函数。算法收敛后,得到一组不变的概率值,即不动点ηα→if(di),利用ηα→if(di)计算每个变量节点的边际概率ηi(di),即
| $ d_i^{BP} = \left\{ {\begin{array}{*{20}{l}} {\;\;\;1\;\;\;\;\;\;\;{\rm{if}}\;\;{\eta _i}\left[ 1 \right] > {\eta _i}\left[ 0 \right],}\\ {\left\{ {0,1} \right\}\;\;\;\;\;{\rm{if}}\;\;{\eta _i}\left[ 1 \right] = {\eta _i}\left[ 0 \right],}\\ {\;\;\;0\;\;\;\;\;\;\;{\rm{if}}\;\;{\eta _i}\left[ 1 \right]{\rm{ < }}{\eta _i}\left[ 0 \right]} \end{array}} \right.。$ | (3) |
BP算法的伪代码描述如下。
输入:因子图模型,最大迭代次数tmax。
输出:固定点ηα→if。
begin
初始时刻t=0, 对因子图中的每一条边(α, i)随机赋值ηα→i(0)∈{0,1};
for t=1 to tmax
按顺序对边(α, i)调用BP算法的迭代方程对ηα→i进行更新:ηα→i(t)←ηα→i(t-1);
如果因子图中所有的边都满足ηα→i(t)=ηα→i(t-1),算法结束并使ηα→if=ηα→i(t);
end for
如果t≥tmax,算法不收敛;如果t<tmax,算法收敛并返回固定点ηα→if;
end
2 求解0-1背包问题的BP算法 2.1 0-1背包问题的线性规划根据0-1背包问题的特点,定义以下向量:对于有n个物体的0-1背包问题,物体的价值属性为w=(w1, w2, …, wn),物体的重量属性为D=(D1, D2, …, Dn)。根据问题的求解需求,特别地定义物体的标签属性为x=(x1, x2, …, xn)T。标签xi=1,表示该物体装入背包;标签xi=0,表示该物体不装入背包。背包载重定义为C,0-1背包问题的线性规划(linear programming, LP)如下:
| $ \begin{array}{l} {\rm{maximize}}\;\;\;\;\;\mathit{\boldsymbol{w}}{\rm{ }}\mathit{\boldsymbol{x}}\\ {\rm{subject to}}\;\;\;\;\;\mathit{\boldsymbol{Dx}}{\rm{ }} \le C\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_i} \in 0, 1 \end{array} $ |
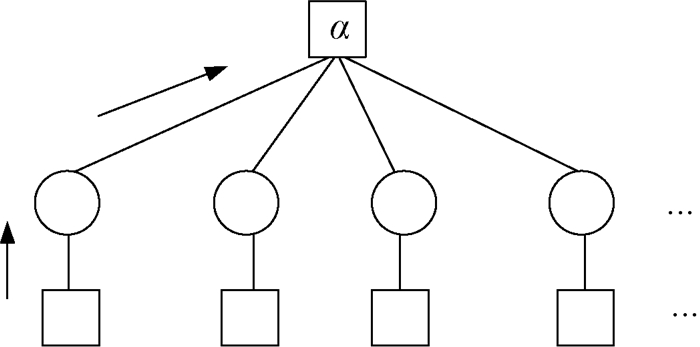
将线性规划中的约束条件转化为因子图中的子句节点,决策变量转化为因子图中的变量节点。根据约束条件中约束函数与所属变量的统计关系,将对应的变量节点与子句节点以边相连,得到0-1背包问题的因子图模型,如图 2所示。图中载重约束为因子图中的因子节点α,其余与各自变量相连的因子节点为各自变量的状态约束节点。
|
图 2 0-1背包问题的因子图模型 Fig. 2 The factor graph model of 0-1 knapsack problem |
在0-1背包问题的因子图模型基础上,设计求解0-1背包问题的BP算法,算法的迭代方程同(1)、(2)。其中,针对该问题设置算法中对应的标识函数为
| $ \begin{array}{*{20}{l}} {S\left( {X_0^\alpha } \right) = 1,\;\;{\rm{if}}\;\;\;{\bf{Dx}} \le C,}\\ {S\left( {X_0^\alpha } \right) = 0,\;\;{\rm{if}}\;\;\;{\bf{Dx}} > C} \end{array}。$ |
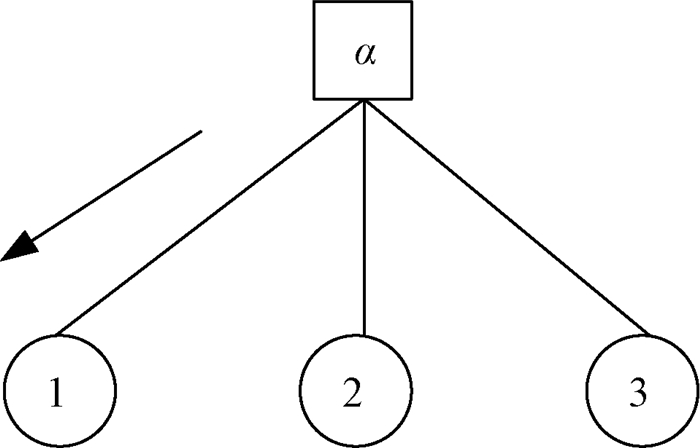
在正向传播过程中,主要考虑边上信息的初始化。为与线性规划的目标函数契合,设置每条边上的初始信息ewx。调用BP算法的迭代方程,以此初始概率沿着因子图的边进行传播更新,设定与图 2中箭头方向相反的方向为反向传播。在反向传播过程中,子句节点传给变量节点的信息需要根据其他变量节点传给它的概率信息来确定。用3个物体的简单实例因子图来说明反向传播过程,如图 3所示。图中的子句节点表示背包的容量约束函数。3个圆形为变量节点,表示有3个物体。假设这3个物体的重量依次为D1=2,D2=2,D3=4,背包载重为5,子句节点的函数为D1+D2+D3≤5。以节点1的信息获得为例,根据物体2和物体3的标签状态排列组合,可得如表 1所示的物体状态分布情况。
|
图 3 简单实例因子图 Fig. 3 Factor graph for simple examples |
|
|
表 1 物体状态分布情况 Tab. 1 State distribution of objects |
表 2描述的是在表 1的4种分布情况下x1=0的状态分布情况,即第1个物体不放进背包。显然,在这个实例中,前3种情况为可行解。根据迭代方程,第1个物体不装包的概率为:P(x1=0)=1×P(1)+1×P(2)+1×P(3)+0×P(4),其中P(1)=P(x1=0)×P(x2=0)×P(x3=0), P(2)=P(x1=0)×P(x2=0)×P(x3=1), P(3)=P(x1=0)×P(x2=1)×P(x3=0),这个计算过程体现了BP算法"和"与"积"的过程。
|
|
表 2 x1=0的状态分布情况 Tab. 2 State distribution at x1=0 |
表 3描述的是在表 1的4种分布情况下x1=1的状态分布情况,即第1个物体放进背包。原理如上,只有第1、3种情况为可行解,则第1个物体装包的概率为:P(x1=1)=1×P(1)+0×P(2)+1×P(3)+0×P(4)。
|
|
表 3 x1=1的状态分布情况 Tab. 3 State distribution at x1=1 |
从子句节点到变量节点一次迭代的信息更新过程如上文所述,在该信息的基础上继续调用BP算法进行新一轮的传播求解,直至算法收敛。算法收敛后得到一组固定点ηα→if,根据这组概率值分别计算每个变量的边际概率。由变量的边际概率判断该物体是否装包,具体方法为:如果该物体取xi=1的概率大于取xi=0的概率,则物体装包;否则,物体不装包。对每个物体进行计算判断,最终得到0-1背包问题的解。
BP算法求解0-1背包问题的伪代码描述如下。
输入:0-1背包问题的因子图模型以及物体的重量D,物体的价值w,背包的载重C;最大迭代次数tmax。
输出:一组固定点ηα→if。
begin
对因子图上各子句节点到变量节点的边赋值ewx;
for t=1 to tmax
调用改进后的BP算法,利用迭代方程在因子图上进行信息更新;
如果因子图中所有的边都存在ηα→i(t)=ηα→i(t-1),算法结束并使ηα→if=ηα→i(t);
如果t<tmax,算法收敛并返回固定点ηα→if;否则,算法不收敛;
end
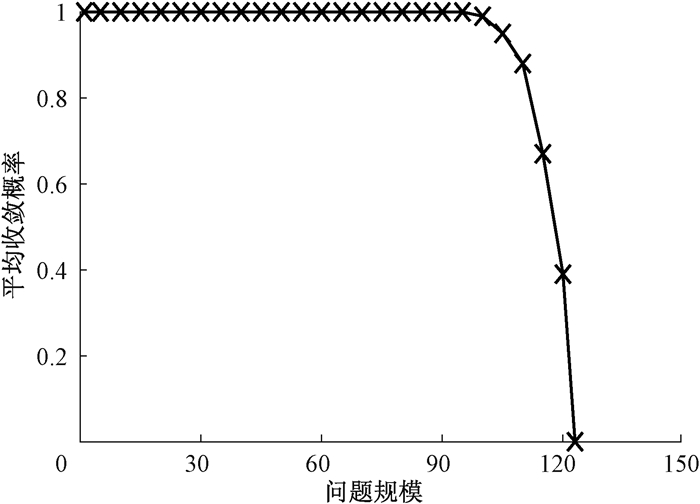
3 数值实验及分析在数值实验中采用随机生成数据集的方法,设置不同的问题规模,在相同问题规模的情况下随机生成多组不同实例进行算法性能验证。BP算法收敛即可计算得到问题的解,也说明了该算法求解的有效性。不同问题规模下BP算法的收敛情况如图 4所示。不同问题规模分别随机生成100组实例并求解,统计收敛情况,最终生成收敛概率。可以看出,用BP算法结合线性规划解决0-1背包问题,问题规模在100以内均以概率1收敛,性能良好。但由于0-1背包问题是一类复杂度较高的NP完全问题,随着问题规模的增大,算法后期收敛性能下降。
|
图 4 不同问题规模的平均收敛概率 Fig. 4 Average convergence rate of different problem scales |
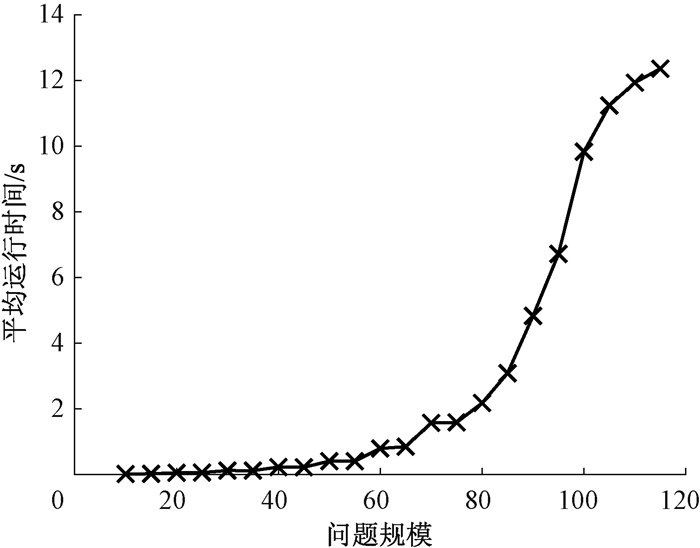
利用BP算法求解不同问题规模所需的平均运行时间如图 5所示。每个数据点由100组随机实例构成,统计得出不同问题规模下求解0-1背包问题的平均运行时间。可以发现,在线性规划基础上,结合BP算法求解0-1背包问题的时间复杂度与问题规模成正比。造成这一现象的原因是随着问题规模的增大,0-1背包问题的解空间也不断增大,算法求解的速度相应降低。
|
图 5 不同问题规模的平均运行时间 Fig. 5 Average running time of different problem scales |
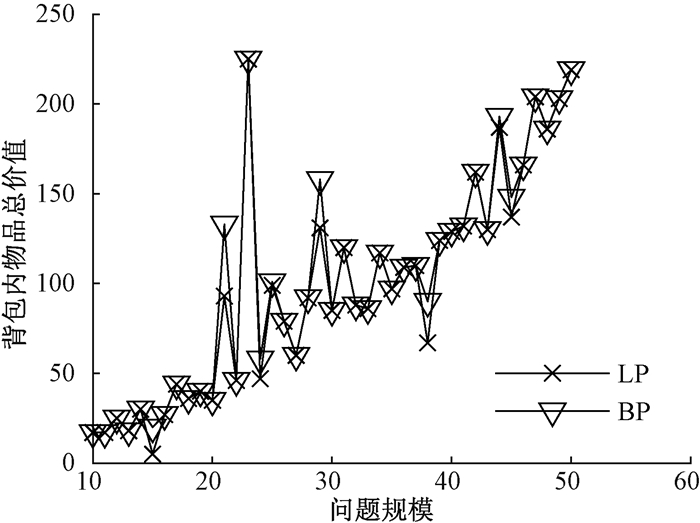
通过与线性规划(LP)对比来说明BP算法的近似性。对于不同的问题规模,分别在随机生成的50个实例上测试LP和BP算法的求解性能,最优解对比结果如图 6所示。可以看出,在不同的问题规模下,BP算法能更有效地找到实例的解,求解质量比LP更优,近似性良好。
|
图 6 LP和BP算法的最优解对比 Fig. 6 Comparison of optimal solutions between LP and BP algorithm |
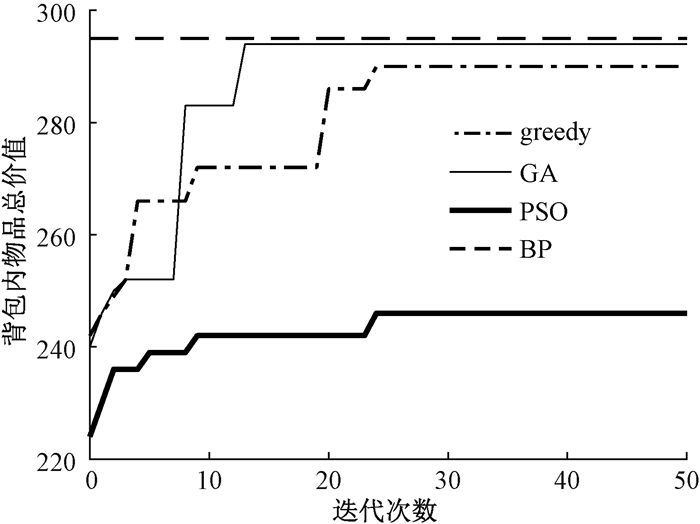
以上实验数据集均为随机产生。为证明算法的鲁棒性,引用文献[18]中0-1背包问题的经典数据集实例1进行实验,该实例的最优解为295,对应总重量为269。使用贪婪算法(greedy)、GA、PSO与本文提出的BP算法进行对比实验,每种算法的迭代次数均为50,4种算法的迭代过程如图 7所示。由求解结果可以看出,BP算法能有效地找到实例的解,提高了求解精确度。
|
图 7 不同算法的迭代过程 Fig. 7 Iterative process of different algorithms |
针对一些启发式算法易陷于局部最优和寻优精度低的缺点,设计了一种求解0-1背包问题的BP算法,实验结果证实了该算法具有较强的全局寻优能力。进一步降低算法求解复杂度以及解决更大规模的难问题是接下来的研究重点,在其他背包问题上的扩展性也是后续可以研究的方向。
| [1] |
贺毅朝, 王熙照, 李文斌, 等. 基于遗传算法求解折扣{0-1}背包问题的研究[J]. 计算机学报, 2016, 39(12): 2614-2630. HE Y C, WANG X Z, LI W B, et al. Research on genetic algorithms for the discounted {0-1} knapsack problem[J]. Chinese journal of computers, 2016, 39(12): 2614-2630. DOI:10.11897/SP.J.1016.2016.02614 (  0) 0) |
| [2] |
RONG A Y, FIGUEIRA J R, KLAMROTH K. Dynamic programming based algorithms for the discounted {0-1} knapsack problem[J]. Applied mathematics and computation, 2012, 218(12): 6921-6933. DOI:10.1016/j.amc.2011.12.068 (  0) 0) |
| [3] |
HE Y C, ZHANG X L, LI W B, et al. Algorithms for randomized time-varying knapsack problems[J]. Journal of combinatorial optimization, 2016, 31(1): 95-117. DOI:10.1007/s10878-014-9717-1 (  0) 0) |
| [4] |
王熙照, 贺毅朝. 求解背包问题的演化算法[J]. 软件学报, 2017, 28(1): 1-16. WANG X Z, HE Y C. Evolutionary algorithms for knapsack problems[J]. Journal of software, 2017, 28(1): 1-16. (  0) 0) |
| [5] |
贺毅朝, 李泽文, 李焕哲, 等. 离散灰狼优化算法求解有界背包问题[J]. 计算机工程与设计, 2019, 40(4): 1008-1015. HE Y C, LI Z W, LI H Z, et al. Discrete grey wolf optimizer for bounded knapsack problem[J]. Computer engineering and design, 2019, 40(4): 1008-1015. (  0) 0) |
| [6] |
王杰, 程学新, 彭金柱. 一种基于粒子群算法优化的加权随机森林模型[J]. 郑州大学学报(理学版), 2018, 50(1): 72-76. WANG J, CHENG X X, PENG J Z. A weighted random forest model based on particle swarm optimization[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(1): 72-76. (  0) 0) |
| [7] |
LIM T Y, AL-BETAR M A, KHADER A T. Taming the 0/1 knapsack problem with monogamous pairs genetic algorithm[J]. Expert systems with applications, 2016, 54(15): 241-250. (  0) 0) |
| [8] |
赵春艳, 郑志明. 一种基于变量熵求解约束满足问题的置信传播算法[J]. 中国科学(信息科学), 2012, 42(9): 1170-1180. ZHAO C Y, ZHENG Z M. A belief-propagation algorithm based on variable entropy for constraint satisfaction problems[J]. Scientia sinica (informationis), 2012, 42(9): 1170-1180. (  0) 0) |
| [9] |
王晓峰, 许道云. RB模型实例集上置信传播算法的收敛性[J]. 软件学报, 2016, 27(11): 2712-2724. WANG X F, XU D Y. Convergence of the belief propagation algorithm for RB model instances[J]. Journal of software, 2016, 27(11): 2712-2724. (  0) 0) |
| [10] |
KIMMIG A, MIHALKOVA L, GETOOR L. Lifted graphical models: a survey[J]. Machine learning, 2015, 99(1): 1-45. DOI:10.1007/s10994-014-5443-2 (  0) 0) |
| [11] |
孙艳歌, 陈旭生, 邵罕, 等. 基于图模型的数据流分类算法[J]. 信阳师范学院学报(自然科学版), 2020, 33(4): 670-674. SUN Y G, CHEN X S, SHAN H, et al. Data stream classification algorithm based on graph model[J]. Journal of Xinyang normal university (natural science edition), 2020, 33(4): 670-674. DOI:10.3969/j.issn.1003-0972.2020.04.027 (  0) 0) |
| [12] |
MARTIN D E K, ASTON J A D. Distribution of statistics of hidden state sequences through the sum-product algorithm[J]. Methodology and computing in applied probability, 2013, 15(4): 897-918. DOI:10.1007/s11009-012-9289-4 (  0) 0) |
| [13] |
SANGHAVI S, MALIOUTOV D, WILLSKY A. Belief propagation and LP relaxation for weighted matching in general graphs[J]. IEEE transactions on information theory, 2011, 57(4): 2203-2212. DOI:10.1109/TIT.2011.2110170 (  0) 0) |
| [14] |
LEE J D, HASTIE T J. Learning the structure of mixed graphical models[J]. Journal of computational and graphical statistics, 2015, 24(1): 230-253. DOI:10.1080/10618600.2014.900500 (  0) 0) |
| [15] |
HUANG J, FREY B J. Cumulative distribution networks and the derivative-sum-product algorithm[J]. Computer science, 2012, 12(1): 290-297. (  0) 0) |
| [16] |
ENGELHARDT A, RIEGER A, TRESCH A, et al. Efficient maximum likelihood estimation for pedigree data with the sum-product algorithm[J]. Human heredity, 2016, 82(1/2): 1-15. (  0) 0) |
| [17] |
WEISS Y, FREEMAN W T. On the optimality of solutions of the max-product belief-propagation algorithm in arbitrary graphs[J]. IEEE transactions on information theory, 2001, 47(2): 736-744. DOI:10.1109/18.910585 (  0) 0) |
| [18] |
柳寅, 马良. 0-1背包问题的模糊粒子群算法求解[J]. 计算机应用研究, 2011, 28(11): 4026-4027, 4031. LIU Y, MA L. Solving 0-1 knapsack problem by fuzzy particle swarm optimization[J]. Application research of computers, 2011, 28(11): 4026-4027, 4031. DOI:10.3969/j.issn.1001-3695.2011.11.006 (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


