2. 上海海事大学 智能信息处理与量子智能计算研究中心 上海 201306;
3. 华东交通大学 信息工程学院 江西 南昌 330013
2. Research Center of Intelligent Information Processing and Quantum Intelligent Computing, Shanghai Maritime University, Shanghai 201306, China;
3. College of Information Engineering, East China Jiaotong University, Nanchang 330013, China
量子图像处理是结合量子计算和数字图像处理技术的一门新兴交叉学科,近20年来得到研究者的广泛关注和深入研究。由于量子力学所特有的叠加、纠缠以及消相干等特性,量子计算机相对经典计算机展现出其独特优势[1-2]。同时,量子计算所呈现的高度并行计算能力,为当今复杂图像处理任务所需的高实时性和安全性的处理提供了一种可行的解决方案[3-4]。因此面对量子计算时代,在量子计算机上实现图形图像处理的功能很有必要性。
在量子计算机上实现图像处理一般分为两个步骤:1)在量子计算机上编码图像信息,即量子图像表示模型;(2)实现量子图像操作和处理的算法[5],类似于经典图像像素的二维表示模型,如文献[6]提出的Qubit Lattice模型, 每个像素存储在一个单独的量子比特当中。文献[7]提出了Real Ket模型,通过不断对图像进行4等分,将图像存储在实值态矢中。文献[8]提出灵活的量子图像表示模型(flexible representation of quantum images, FRQI),利用量子比特序列的计算基态进行叠加,存储图像像素的位置信息,利用与表示位置信息量子比特序列相互纠缠的单量子比特,经角度编码后的量子振幅表示图像的像素信息。虽然FRQI模型大大节省了Qubit Lattice模型表示量子图像所需要的量子比特数量,但是由于FRQI模型通过角度编码将图像的像素信息存储在一个量子比特的振幅当中,因此造成针对图像像素信息的精细和复杂等操作的困难,并且图像像素信息难以精确恢复。为了改进FRQI模型的缺点,文献[9]利用q量子比特序列的基态编码像素灰度范围为[0, 2q-1]的颜色信息,提出了新型增强量子图像表示模型(novel enhanced quantum representation of digital images, NEQR)。随后,研究者们陆续提出了一系列的量子图像表示模型[10-16]。类似于Qubit Lattice模型,文献[10]提出了简易的红外量子图像表示模型(simple quantum representation of infrared images, SQR)。类似于FRQI模型,文献[11]提出了多通道模型的量子彩色图像表示模型(multi-channel representation for quantum images, MCRQI), 文献[12]提出了基于量子相位表示的量子灰度图像模型(flexible quantum representation for gray-level images, FQRGI)。类似于NEQR模型,文献[13]提出了二维叠加态的量子彩色图像表示模型(novel quantum representation of color digital images, NCQI),文献[14]提出了量子索引图像表示模型,文献[15]提出了量子图像比特位平面表示模型(quantum image representation based on bitplanes, BRQI), 以及通用的NEQR表示模型(generalized model of NEQR, GNEQR)[16]。
图像边缘检测技术是图像处理中的基本问题,边缘检测可以去除图像中大量的冗余信息,提取图像的结构、纹理特征等信息,是计算机视觉和模式识别等的基础。因此,在量子计算机上完善图像的边缘检测技术不仅可以加速图像处理的中间过程,同时也为将来在量子计算机上实现计算机视觉和模式识别等问题打下夯实的研究基础,具有重要的研究价值和深远意义。基于经典计算模式,文献[17]提出基于谱聚类的边缘检测算法。文献[18]基于FRQI模型,提出了基于Sobel模板的量子图像边缘提取方案,由于FRQI模型利用角度编码的单量子比特振幅存储像素颜色信息,很难设计有效的量子黑箱操作实现图像的边缘检测过程,量子图像的像素信息难以精确恢复。基于NEQR模型,文献[19]提出了基于零交叉方法的量子图像局部特征点提取方案,但该文献未给出完整的量子线路设计。文献[20]基于量子哈德玛变换提出量子图像的边缘提取方案,但该方案仅仅适用于二值图像。文献[21]基于NEQR模型,提出了基于Sobel算子的图像边缘提取方案。文献[22]提出了基于Laplacian算子增强和零交叉方法相结合的图像边缘提取方案。文献[23]提出了基于Prewitt算子模板的4个梯度方向和非极大值抑制方法的量子图像边缘提取方案。但是在文献[21-23]中,基于单幅的量子图像,简单地通过量子循环移位[24]和受控非门等操作,并不能真正实现量子图像8邻域内像素集的制备,所以这些方案中的量子线路设计存在缺陷。文献[25]提出基于NEQR模型的量子图像边缘检测算法,主要包含3个步骤:1)量子图像平滑;2)基于阈值的梯度计算;3)边缘跟踪。虽然文献[25]给出了图像边缘检测算法的详细步骤,但算法中很多边缘检测步骤并没有设计具体的量子线路以及缺乏量子图像边缘检测完整的线路设计。文献[26]基于NEQR模型提出量子图像的Marr-Hildreth边缘检测算法,该算法主要分为两个步骤:1)基于LoG(Laplacian of Gaussian)滤波器的平滑滤波;2)基于零交叉方法检测图像边缘。但是基于LoG算子的边缘检测算法中,当图像平滑效果越明显,检测到的图像边缘细节信息丢失就越严重,边缘定位就越不准确。
为克服上述量子图像边缘检测方案中存在的缺陷,本文提出基于NEQR模型的量子图像Canny边缘检测算法以及完整的量子线路设计,并对量子线路的复杂度进行分析。最后通过经典计算机上的Matlab软件给出实验结果仿真,以及和其他边缘检测算法方案的对比分析。实验结果表明,基于Canny算法的量子图像边缘检测方案可以检测出更多的边缘细节信息,并且边缘的连接性更好、定位性更优。
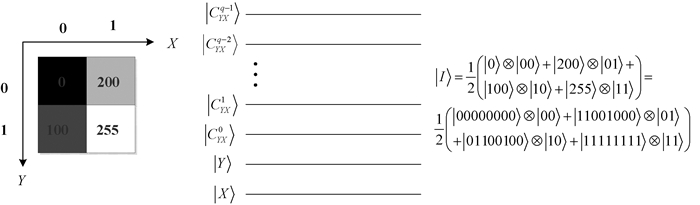
1 基础知识 1.1 NEQR模型文献[9]提出的量子图像NEQR模型,采用2n+q量子比特序列存储一幅大小为2n×2n、灰度值范围为[0, 2q-1]的数字图像,规范化的量子叠加态描述为
| $ |I\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {C_{YX}}\rangle |YX\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} {\mathop \otimes \limits_{i = 0}^{q - 1} } } |C_{YX}^i\rangle |Y\rangle |X\rangle , $ | (1) |
其中:q量子比特序列|CYX〉=|CYXq-1CYXq-2…CYX1CYX0〉表示图像像素在位置(Y, X)处的颜色信息;n量子比特序列|Y〉=|yn-1yn-2…y1y0〉和|X〉=|xn-1xn-2…x1x0〉分别表示图像像素在垂直和水平方向上的位置信息。
图 1给出了一幅大小为2×2灰度图像的量子线路表示,以及对应的量子态表示的实例。
|
图 1 一幅2×2灰度图像的量子线路和相应的量子态表示 Fig. 1 Quantum circuit and corresponding quantum state expression for a 2×2 grayscale image |
Canny边缘检测算法[27]是由国外学者John F. Canny在1986年提出的,创立了边缘检测计算理论,解释如何实现图像的边缘检测。Canny算法定义了最优边缘准则满足的3个条件:1)最优检测。算法能够尽可能多地标识出图像中的实际边缘,漏检真实边缘的概率和误检非边缘的概率都尽可能小;2)最优定位准则。检测到的边缘点的位置距离实际边缘点的位置最近,或者是由于噪声影响引起检测出的边缘偏离物体的真实边缘的程度最小;3)检测点与边缘点一一对应。算子检测的边缘点与实际边缘点应该是一一对应。
Canny边缘检测算法分为5个基本步骤:1)应用高斯滤波平滑图像,消除噪声对边缘检测的影响;2)找寻图像的强度梯度,通常采用一阶有限差分计算图像的梯度幅值和方向;3)应用非极大值抑制消除边缘误检;4)采用双阈值算法决定潜在的边界;5)利用滞后技术来跟踪边界。
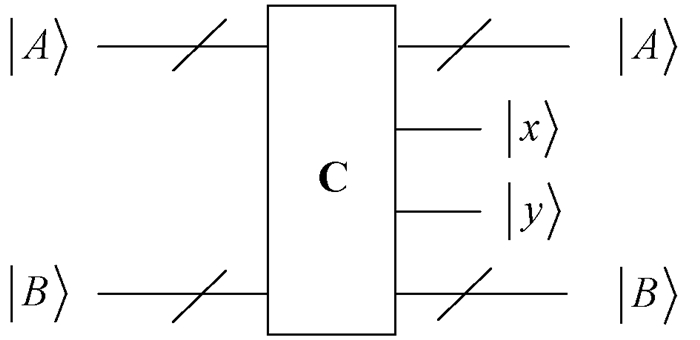
1.3 量子线路模块 1.3.1 量子比较器(C)基于单量子比特比较器UC[28],多量子比特的量子比较器C模块示意图如图 2所示[29]。对于两个n量子比特的数|A〉=|an-1an-2…a1a0〉和|B〉=|bn-1bn-2…b1b0〉,A和B比较的结果可以通过输出量子比特|xy〉描述为:如果x=y=0,则A=B;如果x=1,y=0,则A>B;如果x=0,y=1,则A < B。
|
图 2 量子C模块的线路设计 Fig. 2 Circuit implementation for quantum C module |
对于n量子比特|Y〉=|yn-1yn-2…y1y0〉,CST模块可以实现相应的模2n加1和模2n减1运算[29]。图 3给出了CST模块线路的两种形式:CST(+1)和CST(-1),即有
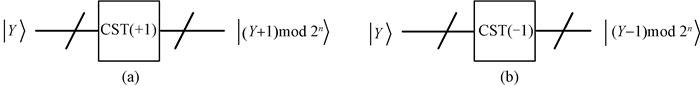
|
图 3 CST(+1)和CST(-1)模块的示意图 Fig. 3 Diagram of CST(+1) and CST(-1) modules |
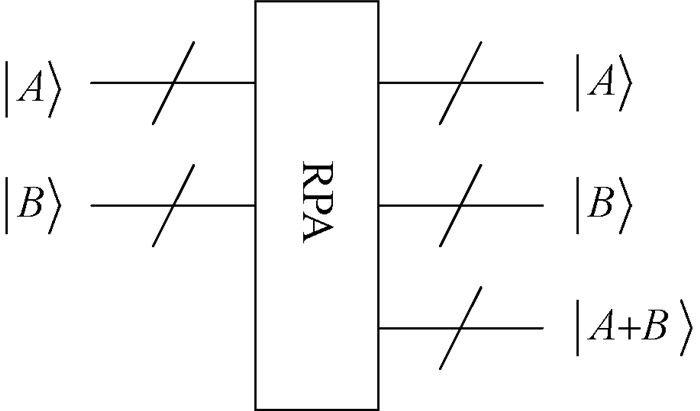
对于两个n量子比特的|A〉和|B〉,量子RPA模块可以计算A+B的和[29]。量子RPA模块如图 4所示。
|
图 4 量子RPA模块 Fig. 4 Quantum module for RPA |
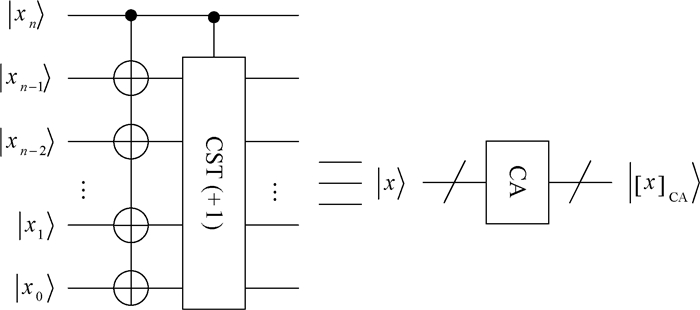
由于二进制比特序列的减法运算可以转化为补码的加法运算,因此可以通过量子RPA模块和补码运算(CA)相结合设计量子减法器的线路设计。假设x=xnxn-1xn-2…x1x0是一个有符号的二进制整数,其中最高比特位xn是符号位(0表示x为整数,1表示x为负数),余下的比特位xn-1xn-2…x1x0是数值比特。对于带符号位的二进制数x的补码运算定义为
| $ {[x]_{{\rm{CA}}}} = \left\{ {\begin{array}{*{20}{l}} {0,{x_{n - 1}}{x_{n - 2}} \cdots {x_1}{x_0},}&{{x_n} = 0}\\ {1,\overline {{x_{n - 1}}{x_{n - 2}}} \cdots \overline {{x_1}{x_0}} + 1,}&{{x_n} = 1} \end{array}} \right., $ | (2) |
其中xk=1-xk, k=0, 1, …, n-1。图 5给出了计算|x〉补码运算的量子线路实现[30]。
|
图 5 量子CA模块的线路设计 Fig. 5 Circuit implementation for quantum CA module |
因此,基于二进制的补码运算,计算两个正整数A与B的减法运算可以表示为
| $ A - B = A + {( - B)_{{\rm{CA}}}} = {[\text{A} + (\bar B + 1)]_{{\rm{CA}}}}, $ | (3) |
其中
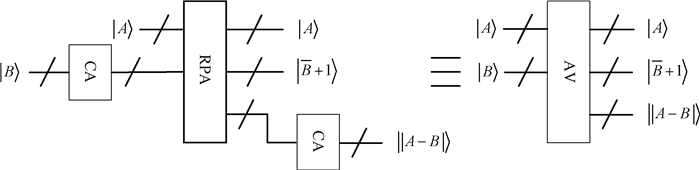
|
图 6 量子AV模块的线路设计 Fig. 6 Circuit implementation for quantum AV module |
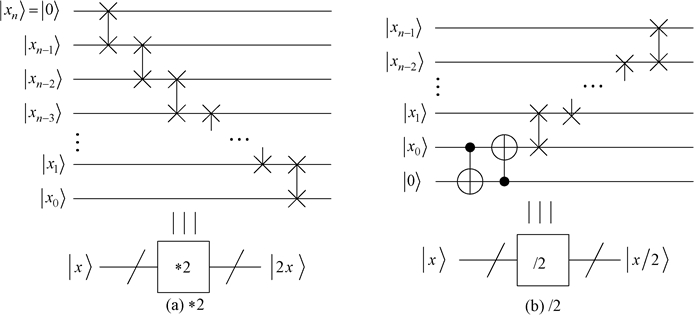
基于量子交换Swap门和借助辅助量子比特|0〉,量子*2和量子/2模块的线路设计如图 7所示[31]。
|
图 7 量子*2和量子/2模块的线路设计 Fig. 7 Circuit implementation for quantum multiplied by 2 and divided by 2 modules |
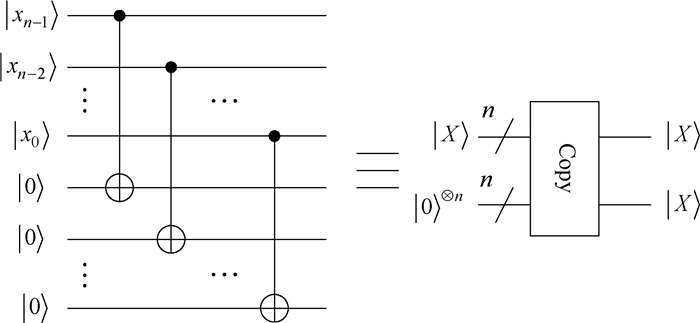
基于量子受控非门(controlled-NOT, CNOT)借助辅助量子比特|0〉,图 8给出了Copy模块的量子线路设计[31]。
|
图 8 量子Copy模块的线路设计 Fig. 8 Circuit implementation for quantum Copy module |
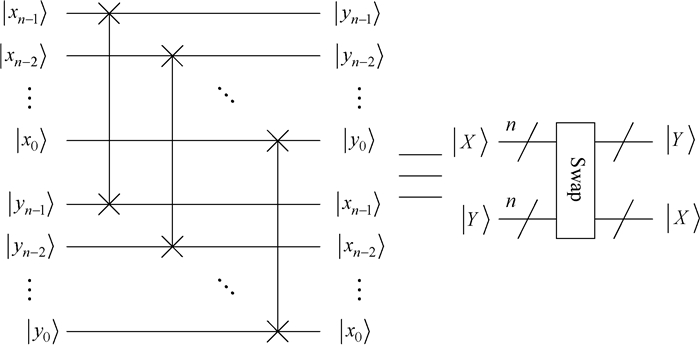
利用n个量子Swap门, 可以实现两个n量子比特序列|X〉和|Y〉之间的相互交换操作。图 9给出了Swap模块的量子线路设计。
|
图 9 量子Swap模块的线路设计 Fig. 9 Circuit implementation for quantum Swap module |
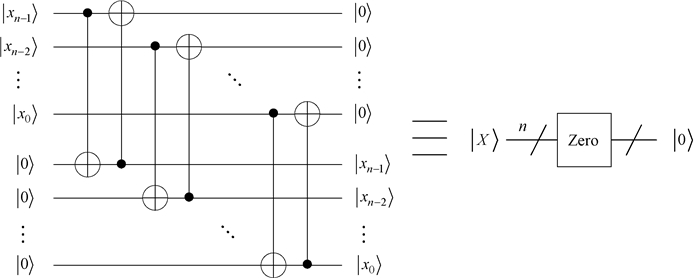
利用2n个CNOT门和借助n个辅助量子比特|0〉⊗n,Zero模块的量子线路设计如图 10所示,即有
|
图 10 量子Zero模块的线路设计 Fig. 10 Circuit implementation for quantum Zero module |
图 11给出了量子图像边缘检测算法流程框架,分为5个步骤:1)高斯平滑;2)梯度计算;3)非极大值抑制;4)双阈值;5)边缘跟踪。

|
图 11 量子图像边缘检测算法流程 Fig. 11 Process of quantum image edge detection algorithm |
高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像去噪。高斯滤波器的卷积模板可以通过计算高斯分布得到,一个二维的高斯函数表示为
| $ G(y,x) = \frac{1}{{2\pi {\sigma ^2}}}{{\rm{e}}^{ - \frac{{{y^2} + {x^2}}}{{2{\sigma ^2}}}}}, $ | (4) |
其中:σ是标准差,反映了数据的离散程度。
要想得到一个高斯滤波器的卷积算子,可以对高斯函数进行离散化,得到的高斯函数值作为模板的系数。一般来说,像素距离卷积算子中心越远,对算子的卷积响应贡献就越小。当σ=0.8,一个3×3大小的高斯卷积算子表示为
| $ G = \frac{1}{{16}}\left[ {\begin{array}{*{20}{l}} 1&2&1\\ 2&4&2\\ 1&2&1 \end{array}} \right]。$ | (5) |
图像高斯平滑滤波过程定义为:使用卷积模板对图像中的每个像素进行扫描,然后计算由模板确定的邻域内像素的加权平均灰度值来代替模板中心像素的值(在本文中称之为高斯响应计算)。基于上述3×3大小的高斯卷积算子,高斯响应计算表示为
| $ \begin{array}{*{20}{l}} {G(Y,X) = (P(Y - 1,X - 1) + 2P(Y - 1,X) + P(Y - 1,X + 1) + 2P(Y,X - 1) + 4P(Y,X) + }\\ {2P(Y,X + 1) + P(Y + 1,X - 1) + 2P(Y + 1,X) + P(Y + 1,X + 1))/16,} \end{array} $ | (6) |
其中:P(Y, X)和G(Y, X)分别为图像经高斯滤波前和滤波后位置(Y, X)处像素的颜色信息。
2.1.1 量子图像制备由于二维叠加态的量子图像表示模型NEQR将一幅图像信息存储在叠加态当中,基于NEQR模型表示的单幅量子图像很难实现图像的高斯平滑滤波。一个可行的方案是制备多幅相同的原始量子图像,通过多幅图像像素之间的计算来代替高斯响应计算。
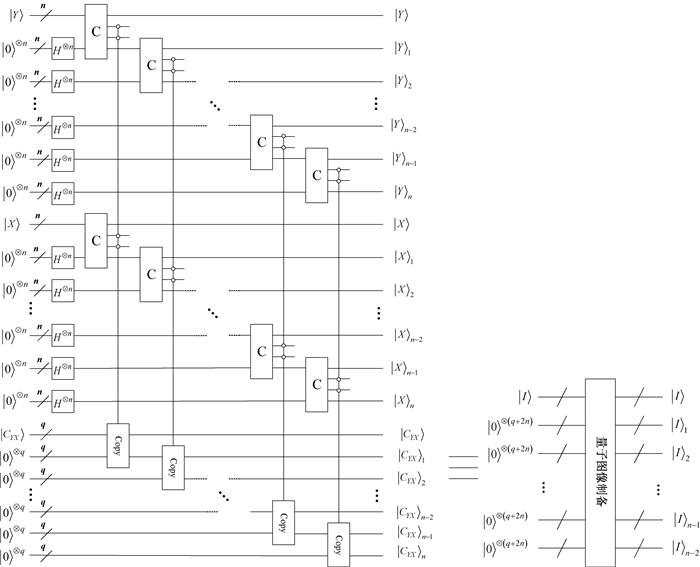
为简化量子线路设计,本文采取式(5)的卷积算子计算量子图像的高斯响应。由于从经典图像制备NEQR量子图像的线路复杂度过高[9],为降低制备多幅量子图像的线路复杂度和充分利用量子计算的并行特性,图 12给出了从一幅量子图像制备额外n幅相同量子图像的线路设计。
|
图 12 量子图像制备模块的线路设计 Fig. 12 Circuit implementation for quantum image preparation module |
如图 12所示,基于NEQR量子图像|I〉(式(1)所示)和一系列辅助量子比特|0〉,通过量子Hadamard(H)变换,C模块和Copy模块可以制备n幅相同的NEQR量子图像|I〉1, |I〉2, …, |I〉n-1, |I〉n,描述为
| $ |I{\rangle _k} = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {C_{YX}}{\rangle _k}|Y{\rangle _k}|X{\rangle _k},k = 1,2, \cdots ,n - 1,n, $ | (7) |
其中:
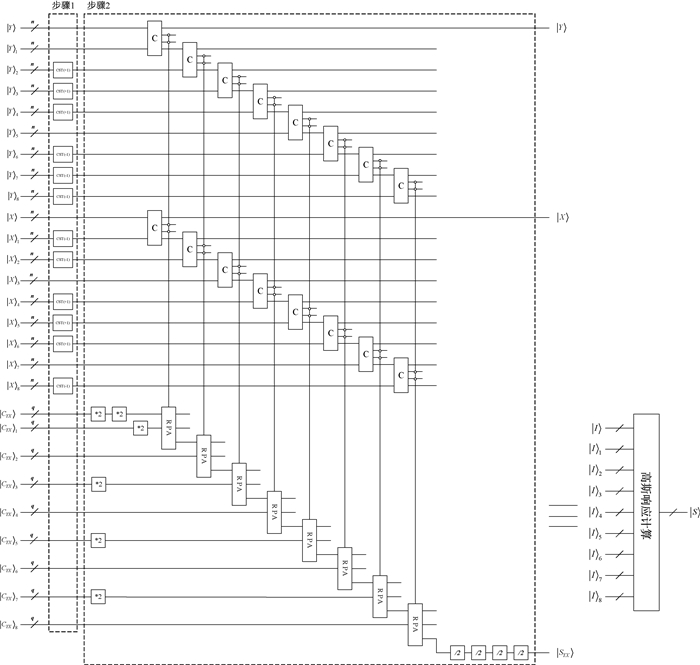
基于图 12所示的量子图像制备模块制备9幅相同的量子图像|I〉, |I〉1, |I〉2, …, |I〉7, |I〉8的基础上,图 13给出了计算量子图像高斯响应的线路设计,主要分为两个步骤。
|
图 13 计算高斯响应的量子线路 Fig. 13 Quantum circuit for calculating the Gaussian response |
步骤1:利用量子CST模块循环平移8幅量子图像|I〉1, |I〉2, …, |I〉7, |I〉8,使得8幅量子图像的像素位于量子图像|I〉对应像素的8邻域内。
步骤2:通过一系列的量子C、量子*2、量子/2和RPA模块,基于9幅量子图像|I〉, |I〉1, |I〉2, …, |I〉7, |I〉8的像素信息计算量子图像的高斯响应。
于是,可以得到经高斯平滑滤波后的量子图像|S〉表示为
| $ \left\{ \begin{array}{l} S\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {S_{YX}}\rangle |Y\rangle |X\rangle ,\\ {S_{Y,X}} = ({C_{Y - 1,X - 1}} + 2{C_{Y - 1,X}} + {C_{Y - 1,X + 1}} + 2{C_{Y,X - 1}} + 4{C_{Y,X}} + 2{C_{Y,X + 1}} + {C_{Y + 1,X - 1}} + 2{C_{Y + 1,X}} + {C_{Y + 1,X + 1}})/16\ 。\end{array} \right. $ | (8) |
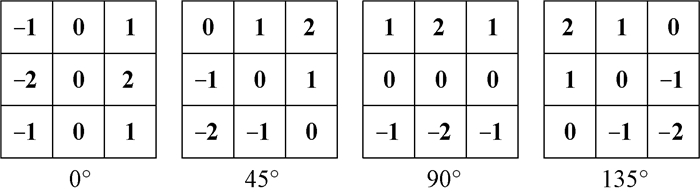
Canny边缘检测算法中的第2步就是用一阶偏导的有限差分来计算经高斯平滑后图像的梯度幅值和方向。梯度计算常用的卷积模板有:Sobel算子、Prewitt算子、Roberts算子等。考虑到Sobel算子对噪声有一定程度的抑制作用,我们选取Sobel算子的4个方向的梯度算子(水平方向,垂直方向,以及两个对角方向)来近似计算图像的梯度幅值和方向。图 14给出了Sobel算子4个方向的卷积算子模板。
|
图 14 Sobel算子4个方向的卷积模板 Fig. 14 Four directional convolution masks of Sobel operator |
基于Sobel算子4个方向的卷积模板,4个方向相应的梯度幅值GYX0、GYX45、GYX90、GYX135计算如下:
| $ \left\{ {\begin{array}{*{20}{l}} {G_{YX}^0 = |[S(Y - 1,X + 1) + 2S(Y,X + 1) + S(Y + 1,X + 1)] - [S(Y - 1,X - 1) + }\\ {2S(Y,X - 1) + S(Y + 1,X - 1)]|;}\\ {G_{YX}^{45} = |[S(Y - 1,X) + 2S(Y - 1,X + 1) + S(Y,X + 1)] - [S(Y,X - 1) + }\\ {2S(Y + 1,X - 1) + S(Y + 1,X)]|;}\\ {G_{YX}^{90} = |[S(Y - 1,X - 1) + 2S(Y - 1,X) + S(Y - 1,X + 1)] - [S(Y + 1,X - 1) + }\\ {2S(Y + 1,X) + S(Y + 1,X + 1)]|;}\\ {G_{YX}^{135} = |[2S(Y - 1,X - 1) + S(Y - 1,X) + S(Y,X - 1)] - [2S(Y + 1,X + 1) + }\\ {S(Y,X + 1) + S(Y + 1,X)]|,} \end{array}} \right. $ | (9) |
其中S(Y, X)表示经高斯平滑后图像位置(Y, X)处的像素灰度值。于是,图像位置(Y, X)处的梯度幅值为GYX=max{GYX0, GYX45, GYX90, GYX135},对应的梯度方向为最大梯度幅值的方向。由于经高斯平滑滤波后只有一幅平滑后的量子图像|S〉,同样需要借助图 12所示的量子图像制备模块额外制备8幅相同的量子图像|S〉。假设经制备得到的8幅量子图像|S〉1, |S〉2, …, |S〉7, |S〉8表示为
| $ |S{\rangle _k} = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {S_{YX}}{\rangle _k}|Y{\rangle _k}|X{\rangle _k};|{S_{YX}}\rangle = |{S_{YX}}{\rangle _k},k = 1,2, \cdots ,7,8, $ | (10) |
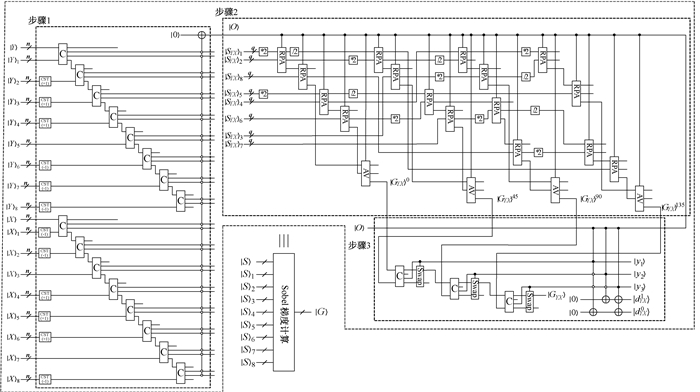
于是,基于9幅相同的量子图像|S〉, |S〉1, |S〉2, …, |S〉7, |S〉8,图 15给出了量子图像Sobel算子梯度计算的线路设计,主要分为以下3个步骤实现。
|
图 15 Sobel梯度计算的量子电路实现 Fig. 15 Quantum circuit implementation for Sobel gradient calculation |
步骤1:首先通过量子CST模块循环平移8幅量子图像|S〉1, |S〉2, …, |S〉7, |S〉8,使得8幅图像的像素信息位于量子图像|S〉像素对应的8邻域内;其次,通过量子C模块比较9幅量子图像的位置信息是否相同,并通过多量子比特控制的受控非门进行标记,即当辅助量子比特|O〉=|1〉,9幅量子图像中像素的位置信息相同;否则,位置信息不同。
步骤2:在9幅量子图像像素位置信息相同的基础上,利用量子*2、量子/2、RPA、AV等模块计算Sobel算子卷积模板4个方向的梯度GYX0, GYX45, GYX90, GYX135。
步骤3:获取图像的梯度幅值以及进行方向标记。首先,通过量子C和Swap模块从4个梯度幅值GYX0, GYX45, GYX90, GYX135中选取最大的梯度幅值GYX;其次,基于3个量子C模块对应的输出量子比特|y1y2y3〉的具体数值,可以确定最大梯度幅值GYX和梯度方向的对应关系,用(y1y2y3,梯度|GYX〉的方向)表示如下:(000,0°),(001,135°),(010,90°),(011,135°),(100,45°),(101,135°),(110,90°),(111,135°)。
基于最大梯度幅值GYX和梯度方向的对应关系,利用多量子比特控制的受控非门,可以借助辅助量子比特|dYX1dYX0〉实现4个方向梯度的标记,即当dYX1dYX0=00时,梯度|GYX〉方向为水平方向0°;当dYX1dYX0=01时,梯度|GYX〉方向为右上对角方向45°;当dYX1dYX0=10时,梯度|GYX〉方向为垂直方向90°;当dYX1dYX0=11时,梯度|GYX〉方向为左上对角方向135°。
基于上述3个步骤的操作,最终得到的量子梯度图像描述为
| $ G\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {G_{YX}}\rangle |d_{YX}^1d_{YX}^0\rangle |Y\rangle |X\rangle 。$ | (11) |
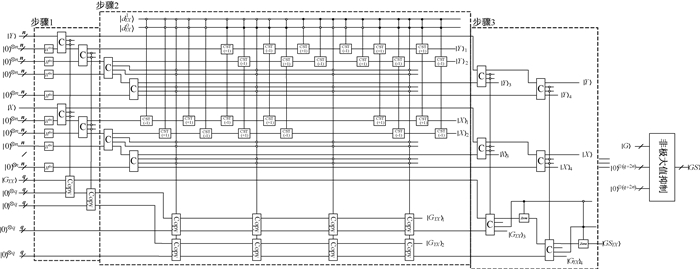
Canny边缘检测算法的第3步是指在梯度方向上实现非极大值抑制。非极大值抑制是指在3×3邻域内,中心像素的灰度值与沿其梯度方向上对应的两个像素相比:如果中心像素的灰度值不小于梯度方向上两个邻域的像素灰度值,则保持中心像素的灰度值不变;否则,将中心像素灰度值置零。这样可以保留局部梯度最大的点,消除边缘的误检。图 16给出了量子梯度图像|G〉非极大值抑制的线路设计,主要有3个步骤。
|
图 16 非极大值抑制的量子线路实现 Fig. 16 Quantum circuit implementation for non-maximum suppression |
步骤1:准备两幅和梯度图像相同的图像|G〉1和|G〉2,以及两幅空白的量子图像|G〉3和|G〉4,表示为
| $ |G{\rangle _k} = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {G_{YX}}{\rangle _k}|Y{\rangle _k}|X{\rangle _k},k = 1,2;|G{\rangle _m} = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {G_{YX}}{\rangle _m}|Y{\rangle _3}|X{\rangle _3},m = 3,4, $ | (12) |
其中:
步骤2:在量子比特|dYX1dYX0〉控制下循环平移两幅量子图像|G〉1和|G〉2,然后将相对应的像素信息存储在两幅量子图像|G〉3和|G〉4当中。
步骤3:在梯度方向,比较梯度幅值|GYX〉和梯度幅值|G〉3、|G〉4的大小从而决定是否抑制|GYX〉,即当|GYX〉 < |GYX〉3或者|GYX〉 < |GYX〉4时,置|GYX〉=|0〉;否则,保持|GYX〉不变。
基于上述3个步骤的操作,可以假设经非极大值抑制后的量子梯度图像描述为
| $ |GS\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } G{S_{YX}}\rangle |Y\rangle |X\rangle 。$ | (13) |
阈值算法是图像边缘检测中的关键环节。阈值选择过小,会检测到过多的虚假边缘,阈值选择过大,则会漏检很多真实的边缘。双阈值法是指选取高低两个阈值系数TH和TL(比率一般为2:1或3:1)来实现对边缘类型的3种划分,具体可以描述为:将小于低阈值TL的点判定为非边缘点;将不小于高阈值TH的点标记为强边缘点(这些点为确定的边缘点);将小于高阈值TH,不小于低阈值TL的点标记为弱边缘点(这些点可能是边缘点, 也可能是非边缘点)。
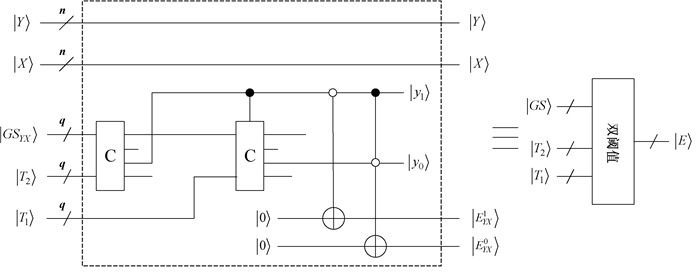
图 17给出了量子图像双阈值判断的线路设计,通过量子比较器和受控非门操作,可以得到包含3种边缘点类型的量子边缘图像表示,
| $ |E\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {E_{YX}}\rangle |Y\rangle |X\rangle , $ | (14) |
|
图 17 双阈值的量子线路实现 Fig. 17 Quantum circuit implementation for dual-threshold |
其中:EYX=EYX1EYX0,EYXi∈{0, 1}, i=1, 2。EYX1EYX0数值与3种边缘点类型之间的对应关系可描述为:当EYX1EYX0=10时,为强边缘点类型;当EYX1EYX0=01时,为弱边缘点类型;当EYX1EYX0=00时,为非边缘点类型。
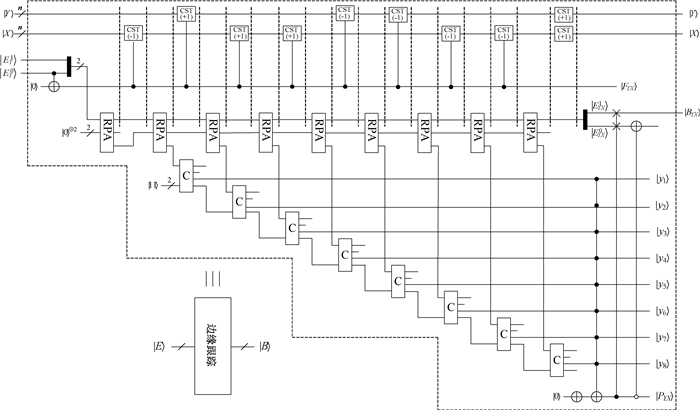
2.5 边缘跟踪基于边缘点类型的3种划分,进一步采用8邻域内的强连通理论将弱边缘点进行正确的划分,从而跟踪边界。图 18给出了量子图像在8邻域内强连通方案的线路设计,主要步骤可以描述如下。
|
图 18 边缘跟踪的量子线路实现 Fig. 18 Quantum circuit implementation for edge tracking |
步骤1:采用受控非门操作,通过辅助量子比特|FYX〉判定当前像素点是否为弱边缘点类型。即当|FYX〉=|1〉,当前的像素点为弱边缘点;否则,当前像素点不是弱边缘点。
步骤2:在量子比特|FYX〉的控制下,利用量子CST模块获取中心像素3×3邻域内像素的灰度信息,并利用量子RPA模块分别计算8邻域内每一个像素的灰度信息与中心像素灰度信息的和。
步骤3:首先,通过量子C模块比较步骤2中计算的和与序列|11〉的大小;然后,利用多量子比特控制的受控非门操作,借助辅助量子比特|PYX〉标记在中心像素的8邻域内是否存在强边缘点。当|PYX〉=|1〉,中心像素的8邻域内存在强边缘点;否则,不存在强边缘点。于是在量子比特|PYX〉的控制下,借助受控的量子Swap门和CNOT门可以实现弱边缘点的正确划分。
基于上述3个步骤的操作,可以得到量子边缘图像的二值化形式描述为
| $ |B\rangle = \frac{1}{{{2^n}}}\sum\limits_{Y = 0}^{{2^n} - 1} {\sum\limits_{X = 0}^{{2^n} - 1} | } {B_{YX}}\rangle |Y\rangle |X\rangle , $ | (15) |
其中:BYX=1表示当前像素为边缘点;BYX=0表示非边缘点。
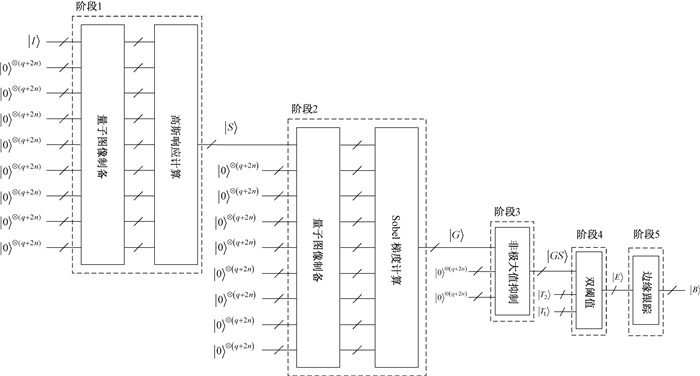
结合量子图像边缘检测算法5个阶段的操作,图 19给出了量子图像Canny边缘检测的完整线路设计。
|
图 19 量子图像Canny边缘检测线路设计 Fig. 19 Circuit design for quantum image Canny edge detection |
基于单量子比特NOT门(也称X门)和双量子比特CNOT门是量子计算中通用的逻辑门组合[32],本文将单量子比特和双量子比特的量子门线路复杂度视为单位1。在此基础上,我们通过计算量子线路可以分解为单量子比特和双量子比特量子门的数目来评价量子线路的复杂度。文献[32]指出3量子比特的Toffoli门可以分解为5个双量子比特门,因此Toffoli门对应的复杂度为5。n量子比特的受控非门Cn-1(X)(控制量子比特的数目为n-1)可以分解为2(n-1)个Toffoli门和1个CNOT门的量子线路[32],于是可以计算得到Cn-1(X)门线路复杂度为2(n-1)×5+1=10n-9。
基于上述介绍的量子线路分解理论,我们首先分析基本量子线路模块的复杂度。
文献[29]中指出,比较两个n比特数值大小的量子C模块(如图 2所示)的线路复杂度为Ο(n),n量子比特的CST模块(如图 3所示)的线路复杂度为Ο(n2),计算两个n比特数值和的量子RPA模块(如图 4所示)的线路复杂度也为Ο(n)。
量子AV模块线路如图 6所示, 包含2个量子CA模块和1个量子RPA模块。于是,可以得到量子AV模块的线路复杂度为Ο(n2)。
量子*2模块线路设计如图 7(a)所示, 包含n个Swap门,复杂度为n。量子/2模块线路设计如图 7(b)所示, 包含(n-1)个Swap门和2个CNOT门,复杂度为n+1。
量子Copy模块线路设计如图 8所示, 包含n个CNOT门,复杂度为n。量子Swap模块线路设计如图 9所示,包含n个Swap门,复杂度为n。量子Zero模块线路设计如图 10所示,包含2n个CNOT门,复杂度为2n。
量子图像Canny边缘检测的模块化完整线路设计如图 19所示,主要分为5个阶段的操作。因此,分阶段分析量子线路的复杂度,然后计算5个阶段的线路复杂度之和便可以得到本文方案量子线路的复杂度。
阶段1:量子图像高斯平滑包括量子图像制备和高斯响应计算两个子模块。量子图像制备模块的线路设计如图 12所示,可知额外制备8幅相同的量子图像应包含16n个H门,16个量子C模块,8个量子Copy模块。高斯响应计算模块的线路设计如图 13所示,包含12个量子CST模块,16个量子C模块, 8个量子RPA模块,6个量子*2模块,以及4个量子/2模块。基于上述分析,量子图像高斯平滑的线路复杂度为
| $ 16n + 32 \cdot O(n) + 8q + 12 \cdot O({n^2}) + 8 \cdot O(q) + 6q + 4(q + 1) = O({n^2})。$ | (16) |
阶段2:量子图像梯度计算包括量子图像制备和Sobel梯度计算两部分。Sobel梯度计算模块的线路设计如图 15所示,包含17个量子C模块,12个量子CST模块,16个量子RPA模块,4个量子AV模块,8个量子*2模块,2个量子/2模块,3个量子Swap模块,1个C32(X),1个C4(X),1个C3(X),2个Toffoli门。基于上述分析,量子图像梯度计算阶段的复杂度计算为
| $ \begin{array}{*{20}{l}} {16n + 33 \cdot O(n) + 12 \cdot O({n^2}) + 16 \cdot O(q) + 4 \cdot O({q^2}) + 16q + 2(q + 1) + }\\ {3q + (32 \times 5 + 1) + (4 \times 5 + 1) + (3 \times 5 + 1) + (2 \times 5) = O({n^2} + {q^2})}。\end{array} $ | (17) |
阶段3:量子图像非极大值抑制的线路设计如图 16所示,包含14个量子C模块,24个量子CST模块,10个量子Copy模块,2个量子Zero模块。基于上述分析,量子图像非极大值抑制阶段的复杂度计算为
| $ 14 \cdot O(n) + 24 \cdot O({n^2}) + 10q + 2 \times 2q = O({n^2})。$ | (18) |
阶段4:量子图像双阈值的线路设计如图 17所示,包含2个量子C模块,1个Toffoli门,1个CNOT门。于是,量子双阈值阶段的线路复杂度为Ο(n)。
阶段5:量子图像边缘跟踪的线路设计如图 18所示,包含10个量子CST模块,8个量子C模块,9个量子RPA模块,1个Toffoli门,2个CNOT门。量子图像边缘跟踪阶段的复杂度为Ο(n2)。
综合上述5个阶段的线路复杂度,可以得到本文提出的量子图像Canny边缘检测的线路复杂度为Ο(n2+q2)。在经典计算机上,由于只能实现单一像素的逐个处理,针对一幅大小为2n×2n灰度图像,经典数字图像的边缘检测算法的复杂度不小于Ο(22n)。与此相反,由于量子计算的高度并行计算能力,量子图像边缘检测算法相比于经典数字图像算法可以实现指数加速。
4 实验结果和分析由于目前还没有功能齐全的实用量子计算机,本文提出的量子图像边缘检测算法通过经典计算机上的Matlab软件仿真。利用Matlab中的单位向量和酉矩阵可以分别等价代替量子态和量子门的酉运算,所以采用经典计算机上的仿真方式虽然不是真正意义上的量子方式仿真,但能仿真量子算法的执行步骤,能够从理论上验证量子算法的有效性。图 20给出了4幅用于实验仿真的灰度图像,从左到右分别为:莱娜,摄影师,山魈,喷气式飞机。

|
图 20 实验中所用的4幅测试图像 Fig. 20 Four tested images used in the experiment |
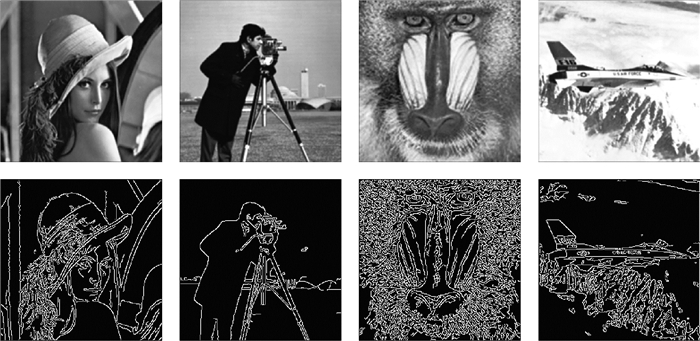
图 21给出了基于本文方案的量子图像高斯平滑滤波和边缘检测的实验效果。图 21中第一行中的图像是高斯滤波后的效果,可以看出经高斯平滑后的图像相比较原始图像变得模糊,图像的对比度有所降低。图 21中第二行中的图像是经边缘检测后得到的二值图像,可以看出检测到的边缘信息丰富,边缘连接性和定位性比较准确。
|
图 21 基于本文方案的量子图像高斯平滑滤波和边缘检测视觉效果 Fig. 21 Visual effects of quantum image Gaussian smoothing and edge detection based on our investigated scheme |
为比较本文方案与其他边缘检测算法的效果,图 22给出了基于经典算法Roberts、Prewitt、Sobel、Zerocross、LoG、Canny算子的边缘检测效果。从实验效果可以看出,相比Roberts、Prewitt、Sobel、Zero-cross、LoG边缘检测算法,本文提出的量子图像Canny边缘检测算法能够检测到一些真正的弱边缘,提取的边缘信息更加丰富,边缘的定位精度高、连接性好。同时,也可以看出本文方案与经典Canny边缘效果差异较小。

|
图 22 不同边缘检测算法的视觉效果 Fig. 22 Visual effects of different edge detection algorithm |
仅通过视觉上的判断很难说明本文方案与其他边缘检测算法的明显差异。均方误差(mean square error,MSE)反映了估计量与被估计量之间的差异程度,可以用来比较两幅图像之间的相似性程度。两幅图像之间的相似性越大,MSE数值就越大。对于两幅大小为2n×2n的单色图像I和E,MSE定义为
| $ MSE = \frac{1}{{{2^n} \times {2^n}}}\sum\limits_{i = 0}^{{2^n} - 1} {\mathop \sum \limits_{j = 0}^{{2^n} - 1} } {[I(i,j) - E(i,j)]^2}。$ | (19) |
考虑Canny算法是边缘检测中公认的标准算法,具有较优的边缘检测性能。本文将基于Canny算法检测得到的边缘图像作为参考图像。表 1给出了不同边缘检测算法得到边缘图像与参考图像的均方误差值。从表 1中的数值可以看出,除了山魈图像外,本文方案的MSE数值比大部分的边缘检测算法(Prewitt、Sobel、Zero-cross、LoG算子)要低,可以说明本文方案检测的边缘图像与经典Canny算法检测的边缘图像更相似。本文方案中山魈图像的MSE值大于其他边缘检测算法的主要原因是山魈图像中含有丰富的边缘细节信息,基于Roberts、Prewitt和Sobel算子检测的边缘细节信息较少,而基于Zero-cross、LoG算子以及本文方案检测的边缘细节信息丰富,导致出现误检的概率也会增加。因此,基于本文方案、Zero-cross和LoG算子检测到的边缘图像MSE数值明显大于Roberts、Prewitt和Sobel算子对应的MSE数值。
|
|
表 1 不同边缘检测方法的MSE Tab. 1 The MSE of different edge detection methods |
针对现有量子图像边缘检测算法的一些不足,本文提出基于NEQR模型的量子图像Canny边缘检测算法,以及完整的量子线路设计。重点实现了图像边缘检测算法中量子图像高斯平滑滤波、梯度计算、非极大值抑制和边缘跟踪的量子线路设计。于经典边缘检测算法相比,量子图像边缘检测算法充分利用量子计算的高度并行能力,线路复杂度的分析表明量子方案具有指数加速。与现有的量子图像边缘检测算法相比,Canny边缘检测算法具有更好的边缘检测性能。虽然本文仅仅给出了Canny边缘检测算法的量子实现方案,相比经典方案在边缘检测性能方面并未有所提高,但该方案构建了量子算法的完整功能线路实现,可在将来的量子计算机上执行,并且具有更高的并行性和处理速度。
在本文设计的方案中只考虑到整数形式的高斯卷积模板和全局阈值的双阈值方案,量子图像的边缘检测性能依然存在进一步提升的空间。此外,由于缺乏实用量子计算机的仿真,本文方案没有考虑在量子计算机上仿真时噪声等因素的影响,只能借助经典计算机从理论研究的角度上验证方案的可行性。因此,解决上述问题也是我们今后的研究重点。
| [1] |
SIMON D R. On the power of quantum computation[J]. SIAM journal on computing, 1997, 26(5): 1474-1483. DOI:10.1137/S0097539796298637 (  0) 0) |
| [2] |
DEUTSCH D, JOZSA R. Rapid solution of problems by quantum computation[J]. Mathematical and physical sciences, 1992, 439(1907): 553-558. (  0) 0) |
| [3] |
YAN F, ILIYASU A M, LE P Q. Quantum image processing: a review of advances in its security technologies[J]. International journal of quantum information, 2017, 15(3): 1730001. DOI:10.1142/S0219749917300017 (  0) 0) |
| [4] |
CAI Y Q, LU X W, JIANG N. A survey on quantum image processing[J]. Chinese journal of electronics, 2018, 27(4): 718-727. DOI:10.1049/cje.2018.02.012 (  0) 0) |
| [5] |
YAN F, ILIYASU A M, VENEGAS-ANDRACA S E. A survey of quantum image representations[J]. Quantum information processing, 2016, 15(1): 1-35. DOI:10.1007/s11128-015-1195-6 (  0) 0) |
| [6] |
VENEGAS-ANDRACA S E, BOSE S. Storing, processing and retrieving an image using quantum mechanics[C]//Proceedings of SPIE-the International Society for Optical Engineering.Bellingham, 2003: 5105.
(  0) 0) |
| [7] |
LATORRE J I. Image compression and entanglement[EB/OL]. (2005-02-05)[2019-02-20]. https: //arxiv.org/abs/quant-ph/0510031.
(  0) 0) |
| [8] |
LE P Q, DONG F Y, HIROTA K. A flexible representation of quantum images for polynomial preparation, image compression, and processing operations[J]. Quantum information processing, 2011, 10(1): 63-84. DOI:10.1007/s11128-010-0177-y (  0) 0) |
| [9] |
ZHANG Y, LU K, GAO Y H, et al. NEQR: a novel enhanced quantum representation of digital images[J]. Quantum information processing, 2013, 12(8): 2833-2860. DOI:10.1007/s11128-013-0567-z (  0) 0) |
| [10] |
YUAN S Z, MAO X, XUE Y L, et al. SQR: a simple quantum representation of infrared images[J]. Quantum information processing, 2014, 13(6): 1353-1379. DOI:10.1007/s11128-014-0733-y (  0) 0) |
| [11] |
SUN B, ILIYASU A M, YAN F, et al. An RGB multi-channel representation for images on quantum computers[J]. Journal of advanced computational intelligence and intelligent informatics, 2013, 17(3): 404-417. DOI:10.20965/jaciii.2013.p0404 (  0) 0) |
| [12] |
YANG Y G, XIA J, JIA X, et al. Novel image encryption/decryption based on quantum Fourier transform and double phase encoding[J]. Quantum information processing, 2013, 12(11): 3477-3493. DOI:10.1007/s11128-013-0612-y (  0) 0) |
| [13] |
SANG J Z, WANG S, LI Q. A novel quantum representation of color digital images[J]. Quantum information processing, 2017, 16(2): 42. DOI:10.1007/s11128-016-1463-0 (  0) 0) |
| [14] |
王兵, 郝梦奇, 李盼池, 等. 量子索引图像的描述方法与隐写算法[J]. 计算机辅助设计与图形学学报, 2019, 31(11): 1995-2006. WANG B, HAO M Q, LI P C, et al. Description method and steganography of quantum indexed images[J]. Journal of computer-aided design and computer graphics, 2019, 31(11): 1995-2006. (  0) 0) |
| [15] |
LI H S, CHEN X, XIA H Y, et al. A quantum image representation based on bitplanes[J]. IEEE access, 2018, 6: 62396-62404. DOI:10.1109/ACCESS.2018.2871691 (  0) 0) |
| [16] |
LI H S, FAN P, XIA H Y, et al. Quantum implementation circuits of quantum signal representation and type conversion[J]. IEEE transactions on circuits and systems I: regular papers, 2019, 66(1): 341-354. DOI:10.1109/TCSI.2018.2853655 (  0) 0) |
| [17] |
郭新, 徐明, 张众. 基于谱聚类的边缘检测算法[J]. 郑州大学学报(理学版), 2018, 50(3): 83-87. GUO X, XU M, ZHANG Z. A novel edge detection method based on spectral curvature clustering[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(3): 83-87. (  0) 0) |
| [18] |
ZHANG Y, LU K, GAO Y H. QSobel: a novel quantum image edge extraction algorithm[J]. Science China information sciences, 2015, 58(1): 104-116. (  0) 0) |
| [19] |
ZHANG Y, LU K, XU K, et al. Local feature point extraction for quantum images[J]. Quantum information processing, 2015, 14(5): 1573-1588. DOI:10.1007/s11128-014-0842-7 (  0) 0) |
| [20] |
YAO X W, WANG H Y, LIAO Z Y, et al. Quantum image processing and its application to edge detection: theory and experiment[J]. Physical review X, 2017, 7(3): 031041. DOI:10.1103/PhysRevX.7.031041 (  0) 0) |
| [21] |
FAN P, ZHOU R G, HU W W, et al. Quantum image edge extraction based on classical Sobel operator for NEQR[J]. Quantum information processing, 2019, 18(1): 24. DOI:10.1007/s11128-018-2131-3 (  0) 0) |
| [22] |
FAN P, ZHOU R G, HU W W, et al. Quantum image edge extraction based on Laplacian operator and zero-cross method[J]. Quantum information processing, 2019, 18: 27. DOI:10.1007/s11128-018-2129-x (  0) 0) |
| [23] |
ZHOU R G, YU H, CHENG Y, et al. Quantum image edge extraction based on improved Prewitt operator[J]. Quantum information processing, 2019, 18(9): 261. DOI:10.1007/s11128-019-2376-5 (  0) 0) |
| [24] |
LE P Q, ILIYASU A M, DONG F Y, et al. Strategies for designing geometric transformations on quantum images[J]. Theoretical computer science, 2011, 412(15): 1406-1418. DOI:10.1016/j.tcs.2010.11.029 (  0) 0) |
| [25] |
YUAN S Z, VENEGAS-ANDRACA S E, WANG Y C, et al. Quantum image edge detection algorithm[J]. International journal of theoretical physics, 2019, 58(9): 2823-2833. DOI:10.1007/s10773-019-04166-9 (  0) 0) |
| [26] |
LI P C, SHI T, LU A P, et al. Quantum implementation of classical Marr-Hildreth edge detection[J]. Quantum information processing, 2020, 19(2): 1-26. (  0) 0) |
| [27] |
CANNY J. A computational approach to edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 1986, 8(6): 679-698. (  0) 0) |
| [28] |
OLIVEIRA D S, RAMOS R V. Quantum bit string comparator: circuits and applications[J]. Quantum computers and computing, 2007, 7: 17-26. (  0) 0) |
| [29] |
HU W W, ZHOU R G, LIU X A, et al. Quantum image steganography algorithm based on modified exploiting modification direction embedding[J]. Quantum information processing, 2020, 19(5): 1-28. (  0) 0) |
| [30] |
LI P C, WANG B, XIAO H, et al. Quantum representation and basic operations of digital signals[J]. International journal of theoretical physics, 2018, 57(10): 3242-3270. DOI:10.1007/s10773-018-3841-0 (  0) 0) |
| [31] |
LI P C, LIU X D. Bilinear interpolation method for quantum images based on quantum fourier transform[J]. International journal of quantum information, 2018, 16(4): 1850031. DOI:10.1142/S0219749918500314 (  0) 0) |
| [32] |
NIELSEN M A, CHUANG I L. Quantum information theory[M]. Cambridge: Cambridge University Press, 2000.
(  0) 0) |
 2020, Vol. 52
2020, Vol. 52


