电力负荷预测是电网规划的基础,传统电网规划是以整个规划区域为对象,对总负荷进行预测。传统负荷预测方法有增长曲线法、回归分析法和时间序列法[1]。目前模糊预测法、神经网络法[2]也应用于负荷预测之中,称之为现代负荷预测方法。随着对电力系统的管理日益精细化,对于负荷预测也不仅仅局限于精准的总量负荷预测,还要求给出更为精细的负荷空间分布[3]。配电网网格化规划的提出,使得负荷预测过程由原来的整体区域负荷预测变为对供电单元、供电网格、供电区域3个层级自下而上依次展开空间负荷预测。
在配电网网格化规划中,空间负荷预测的精确性与参数的选取直接相关,如负荷密度指标的选取、供电单元内同时率的选取以及供电单元间同时率的考虑。文献[4]基于网格化规划对上饶市经济开发区进行了电力需求预测,供电单元内根据历史负荷进行回归分析来预测近期负荷,饱和年负荷采用负荷密度法进行预测,规划年同时率根据现状值进行选取,由于供电单元是人为划分的区域,其负荷数据需根据配变信息进行统计,因而统计各个单元的历史负荷数据工作量较大。文献[5]基于灰色关联和BP神经网络定量分析了电力、经济、需求侧管理及气候等因素对同时率的影响,并预测规划年同时率,其预测结果是以电力、经济等影响因素的预测为基础的。文献[6]参考国内典型用户的饱和负荷密度指标及其发展规律曲线来确定规划区域内负荷密度指标的选取,未考虑规划区域独有的负荷发展特性。本文提出用统一的S型曲线模型确定各个供电单元过渡年负荷密度指标的方法,既能反映区域内的负荷发展特性,又降低了基础数据统计工作量。同时,给出了供电单元内同时率的日负荷特性曲线叠加方法,以及供电单元间同时率的计算公式,为负荷预测过程中同时率的选取提供一个较为方便有效的方法。
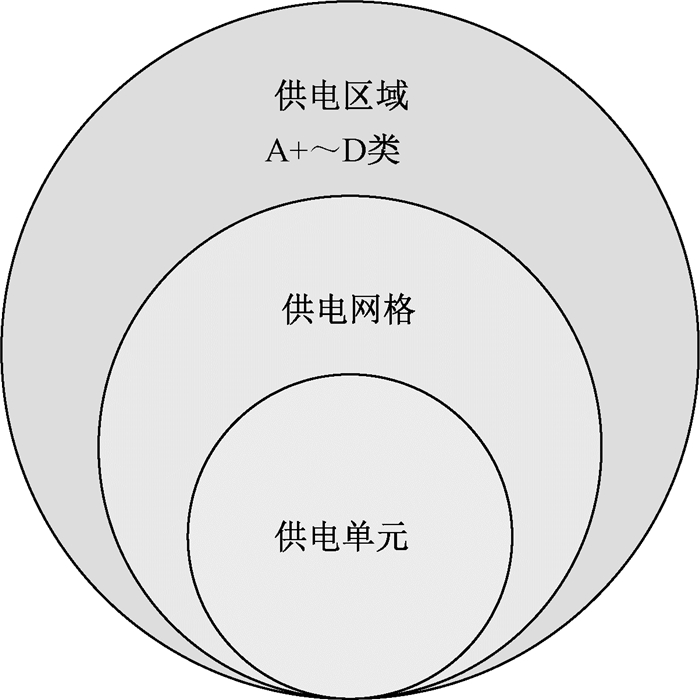
1 网格化规划空间负荷预测传统配电网规划建设模式是以变电站为中心、中压线路向四周延伸。这种辐射式的网架结构会导致:高压变电站供电范围不清晰、容载比分布不均匀;中压线路迂回、交叉供电;低压线路错乱,线损较高[7]。配电网网格化规划是指将配电网供电区域划分为若干供电网格,并进一步细化为供电单元,形成“供电区域、供电网格、供电单元”三级网络[8],自下而上分层分级开展配电网规划,提升了配网规划的精细度,便于运行管理。网格化规划中三级网络关系图如图 1所示。供电区域依据地区行政级别或规划水平年的负荷密度,参考经济发达程度、用户重要性、用电水平、GDP等因素,可划分为A+、A、B、C、D 5类[9]。供电网格是在供电区域划分的基础上,与城乡控制性详细规划等市政规划及行政区域划分相衔接,综合考虑配网运维抢修、营销服务等因素,进一步划分而成的若干相对独立的网格。供电单元是指在供电网格基础上,综合考虑用地属性、负荷密度、供电特性等因素划分的若干相对独立的单元。
|
图 1 网格化三级网络关系 Fig. 1 Three-level network in grid planning |
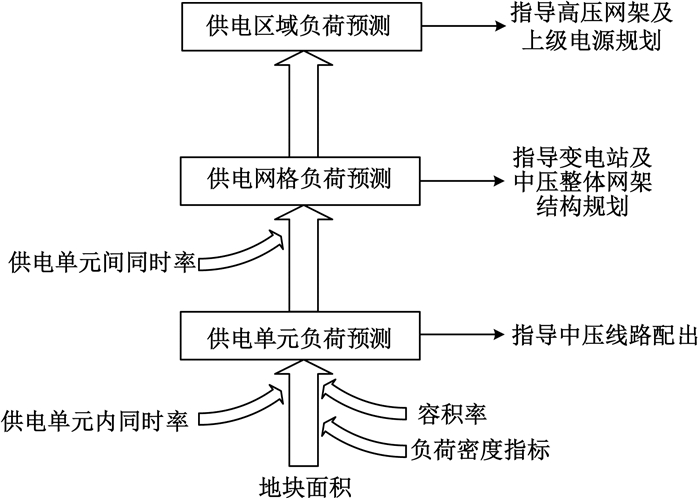
配电网网格化规划中空间负荷预测是对供电单元、供电网格、供电区域3个层级自下而上依次开展负荷预测,对于已完成城乡规划和土地利用规划的区域,由于其用地性质、规模和空间分布已明确,可采用负荷密度法进行负荷预测[10],其负荷预测流程如图 2所示,先通过地块面积、负荷密度指标、容积率以及供电单元内同时率参数计算供电单元负荷,用以指导中压线路配出;再利用供电单元负荷预测结果,并考虑供电单元间同时率,得到供电网格的负荷,可指导高压变电站的容量及布点规划,以及中压整体网架结构规划;最后由供电网格负荷预测结果汇总得到供电区域的负荷水平,由于供电网格为面积较大的综合型区域,它们之间的同时率非常接近1,累加时一般不再考虑同时率。
|
图 2 网格化空间负荷预测流程 Fig. 2 Grid spatial load forecasting process |
对于供电单元来说,负荷由各个地块面积、负荷密度指标、容积率的乘积和以及同时率得到,其中容积率可参考城市控制性详细规划中的地块控制强度指标,供电单元的负荷预测关键问题是如何确定负荷密度指标,特别是过渡年负荷密度指标选取方法以及供电单元内同时率的选取方法。
2.1 负荷密度指标的选取负荷密度指标分为饱和年负荷密度指标和过渡年负荷密度指标。对于同一区域来说,由于其政治、经济等外部环境因素相近,可认为同一用地性质的饱和年负荷密度指标是相似的[11],因此同一区域不同供电单元,虽然其现状负荷水平不同,但其饱和年负荷密度指标可进行统一选取。
饱和年负荷密度指标一般可通过用户调研得到,如调研地区内某发展较为成熟的商场负荷及其面积等信息,将计算出的负荷密度指标作为该地区饱和年商业用地负荷密度指标。除用户调研外,饱和年负荷密度指标的选取也可参考其他发展成熟地区的负荷密度值,或参考一些设计规范资料中的负荷密度指标推荐值。
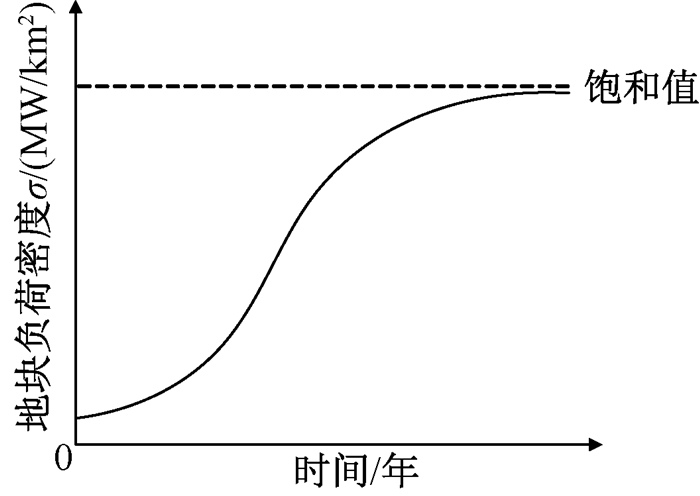
对于负荷密度法预测过渡年负荷,其关键在于确定其过渡年负荷密度指标。由于空间的限制,地块负荷密度不可能无限增长,往往经过一段时间快速增长后,速度逐渐放慢,最后趋向饱和[12],其S型曲线发展趋势如图 3所示。S型曲线通常采用逻辑斯蒂模型进行拟合,其常微分方程为dy/dt=ry(k-y)/k,式中:y为因变量;t为时间;r为增长潜力指数;k为饱和值。S型曲线常微分方程的通解为yt=k/(1+e(-rt+c))。
|
图 3 地块负荷密度发展趋势 Fig. 3 Development trend of land load density |
除负荷密度饱和值外,负荷密度的发展趋势也与政治、经济等外部环境因素相关,因此对于同一区域内各个供电单元来说,虽然负荷发展水平不同,负荷空间分布不均匀,但同一种用地性质的负荷密度S型曲线是相同的,不同的是各个供电单元现状年在S型曲线上所处的位置。
在饱和年负荷密度指标确定的情况下,k为已知量。为了确定过渡年负荷密度指标,需确定S型曲线模型中参数r,以及现状负荷密度指标在曲线上所处的位置。由于参数c仅影响S型曲线的左右平移,不影响曲线形状,因此可令c=0,S型曲线方程变为
| $ {y_t} = k/(1 + {{\rm{e}}^{ - rt}})。$ | (1) |
利用yt=k/(1+e-rt)和yt+1=k/(1+e-r(t+1)),消除参数t, 可得到(yt+1-yt)/yt=(1-er)/kyt+1+er-1。令st+1=(yt+1-yt)/yt,b=(1-er)/k,则st+1=byt+1-kb。通过历史统计数据和最小二乘法可得
在将各类或各分区的负荷相加时,需要考虑同时率的问题。同时率指整个电网最大负荷与各用户最大负荷之和的比值[13]。其大小与区域社会经济发展、季节温度变化以及负荷结构等因素相关[14]。在实际规划中,同时率一般通过典型日负荷特性曲线叠加获得,或是根据经验估计同时率的大小,一般来讲,用电负荷性质越接近同时率越高;反之,若负荷性质差异较大,则同时率就越小。供电单元的叠加典型日负荷特性曲线求取同时率的步骤如下:
1) 根据城市规划,统计汇总区域内各个用地性质用地的面积,合理选取负荷密度指标,计算得出此区域内各个用地性质用地的负荷预测值;
2) 采集典型日不同用地性质的整点负荷,绘制不同用地性质用地的日负荷曲线(标幺值);
3) 将各类用地性质的日负荷曲线乘以各自用地性质用地的负荷预测值后,予以叠加,其曲线最大值与各类用地性质用地的负荷预测值之和的比值,即为此区域的同时率。
3 基于单元负荷的供电网格负荷预测供电网格的负荷可通过网格内各个供电单元的负荷累加之和,并考虑供电单元间同时率得到,其关键问题为如何确定供电单元间同时率。通过对单元内同时率的计算方法分析可知,供电单元内同时率是单元曲线叠加最大负荷与单元各用地负荷直接相加之和的比值。类似地,供电单元间同时率可通过供电网格曲线叠加最大负荷与各个单元最大负荷之和来进行计算。
假设某供电网格A内包含n个供电单元A1,A2,…,An,则n个供电单元间的同时率为
| $ t = ({P_A}\cdot{t_A})/(\sum\limits_n {{{P}'_{An}}} ) = (\sum\limits_n {{P_{An}}\cdot{t_A}} )/(\sum\limits_n {({P_{An}}\cdot{t_{An}})} ), $ | (2) |
式中:PA为不考虑供电单元层级同时率情况下,网格A的负荷(即区域内各个用地性质用地的负荷预测结果之和);PAn为在不考虑单元内同时率情况下,供电单元An的负荷;P′An为供电单元An在考虑单元内同时率后的负荷;tA为不考虑供电单元层情况下,网格A的同时率(可用日负荷特性曲线进行叠加);tAn则为供电单元An的同时率。在以往网格化规划负荷预测过程中,单元间同时率并没有一个明确的选取方法,只有一个大概的选取范围,即0.95~1。式(2)则给出了具体的单元间同时率选取方法,可以在今后的网格化规划负荷预测过程中指导供电单元间同时率的取值。
由于供电网格为面积较大的综合型区域,之间同时率接近于1,因此供电区域的负荷计算方法为供电网格负荷直接累加,不再考虑供电网格间同时率。
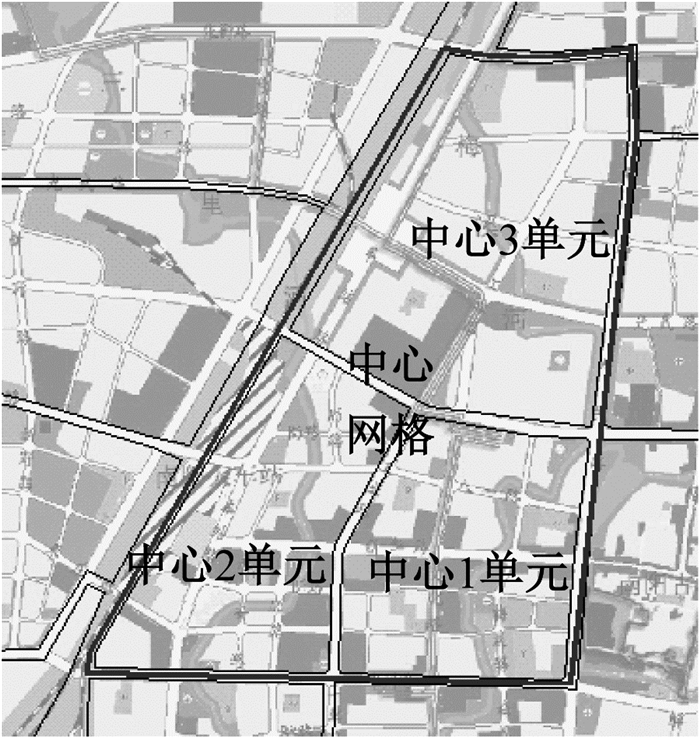
4 算例分析某地区中心网格包含三个供电单元,分别为中心1、中心2和中心3,其单元网格划分及规划土地性质如图 4所示。调研该地区发展较为成熟的各类用户,将其负荷密度值作为该地区饱和年负荷密度指标选取值,其结果分别为:居住用地23 W/m2、商业设施用地47 W/m2、行政办公用地39 W/m2、文化设施用地43 W/m2、教育用地18 W/m2。此网格三个单元的各个用地性质、用地面积、容积率选取值以及饱和年各个用地性质负荷计算如表 1所示,其中容积率取值参考该地区控制性详细规划中控制强度指标,饱和年负荷为用地面积、容积率及对应负荷密度指标的乘积。
|
图 4 中心网格单元划分 Fig. 4 The unit division of central grid |
|
|
表 1 中心网格供电单元用地及负荷情况 Tab. 1 Land and load of power supply unit in central grid |
由表 1可以得出,不考虑同时率情况下,中心1、中心2、中心3三个单元饱和年负荷分别为38.6 MW、31.19 MW、68.48 MW,中心网格的负荷为138.28 MW。
调研该地区内各个用地性质典型用户的典型日负荷特性,绘制日负荷特性曲线(标幺值),以各用地性质负荷作为权重进行曲线叠加,其曲线最高点负荷与单元累加负荷的比值为单元内同时率,则中心网格三个供电单元的饱和年同时率分别为0.893 52、0.963 70、0.978 04,考虑同时率后,中心网格三个供电单元的饱和年负荷分别为34.49 MW、30.06 MW、66.98 MW。
调研该地区内各个用地性质典型用户的负荷密度历史情况,计算负荷密度S型发展曲线模型中两个参数k和r,k为各类用地性质的饱和年负荷密度指标,各类用地性质的参数r分别为居住用地0.171 8、商业设施用地0.175 7、行政办公用地0.160 2、文化设施用地0.158 1、教育用地0.119 3。
根据各个供电单元内典型用户2018年负荷密度数据,确定其在负荷密度S型曲线上的位置,进而可以计算得到规划年的负荷密度指标值。3个供电单元的过渡年负荷密度指标计算值如表 2所示。
|
|
表 2 中心网格供电单元过渡年负荷密度指标 Tab. 2 Transitional annual load density index of power supply unit in central grid |
根据过渡年各指标选取结果,可计算过渡年各个单元的同时率以及负荷情况,结果如表 3所示。
|
|
表 3 中心网格供电单元过渡年负荷 Tab. 3 Transitional annual load in central grid |
在计算出各个单元的负荷及同时率的情况下,2019—2021年以及饱和年供电单元间的同时率可通过式(2)进行计算,结果分别为0.999 50、0.999 41、0.999 31、0.998 09,进而可计算得到中心网格的负荷,其结果分别为109.42 MW、112.34 MW、114.91 MW、131.28 MW。
通过统计2019年中心网格内配变信息,可计算得到各个单元的负荷及同时率情况,可将此实际数据与表 3中理论计算结果进行比较,验证理论计算方法的准确性与可靠性,中心网格及三个供电单元的配变信息统计结果如表 4所示,2019年中心1、中心2、中心3三个供电单元间的同时率可用网格最大负荷与单元最大负荷之和进行计算,其值为0.996 52。中心网格及三个单元2019年实际值与理论计算结果对比如表 5所示。负荷与同时率的误差分别不超过5%、1%,证明了理论计算方法的准确性。
|
|
表 4 中心网格配变信息统计 Tab. 4 Distribution statistics of central grid |
|
|
表 5 中心网格实际值与理论计算结果对比 Tab. 5 Comparison between the actual value of central grid and the theoretical calculation result |
本文根据网格化规划的要求,自下而上给出了供电单元、供电网格、供电区域的负荷预测方法。供电单元层提出了S型曲线确定过渡年负荷密度指标,以及日负荷特性曲线叠加确定供电单元内同时率的方法;供电网格层重点研究了单元间同时率的计算方法,最后进行了算例分析,验证了方法的准确性,对网格化规划中的高中压电网规划奠定坚实基础。
| [1] |
陈志强. 自然区域电网负荷预测及规划的研究[D]. 保定: 华北电力大学(河北), 2009. CHEN Z Q. Research on power load forecasting and transmission network planning of natural areas[D]. Baoding: North China Electric Power University, 2009. (  0) 0) |
| [2] |
邵恒, 冯兴乐, 包芬. 基于深度学习的文本相似度计算[J]. 郑州大学学报(理学版), 2020, 52(1): 66-71, 78. SHAO H, FENG X L, BAO F. Text similarity computation based on deep-learning[J]. Journal of Zhengzhou university(natural science edition), 2020, 52(1): 66-71, 78. (  0) 0) |
| [3] |
肖白, 周潮, 穆钢. 空间电力负荷预测方法综述与展望[J]. 中国电机工程学报, 2013, 33(25): 78-92, 14. XIAO B, ZHOU C, MU G. Review and prospect of the spatial load forecasting methods[J]. Proceedings of the CSEE, 2013, 33(25): 78-92, 14. (  0) 0) |
| [4] |
华蕾. 基于网格化规划的上饶市经济技术开发区电力需求预测[D]. 北京: 华北电力大学, 2018. HUA L. Forecast of power demand in Shangrao economic and technological development zone based on grid planning[D]. Beijing: North China Electric Power University, 2018. (  0) 0) |
| [5] |
田怀源, 张峰, 王新库, 等. 基于灰色关联度和BP神经网络的最大负荷同时率预测方法研究[J]. 山东电力技术, 2017, 44(4): 11-15, 21. TIAN H Y, ZHANG F, WANG X K, et al. Prediction method research on maximum load coincidence factor based on gray relational and BP neural network[J]. Shandong electric power, 2017, 44(4): 11-15, 21. DOI:10.3969/j.issn.1007-9904.2017.04.003 (  0) 0) |
| [6] |
杨慢慢, 王金凤, 李燕青, 等. 改进的空间负荷预测法及其应用[J]. 电力科学与工程, 2011, 27(11): 35-38. YANG M M, WANG J F, LI Y Q, et al. The improved spatial load forecasting and its application[J]. Electric power science and engineering, 2011, 27(11): 35-38. (  0) 0) |
| [7] |
吴怀波, 程金松, 陶军, 等. 城区配电网三级网格化规划及网格划分研究[J]. 国网技术学院学报, 2018, 21(1): 1-4. WU H B, CHENG J S, TAO J, et al. Study on three-level grid planning and grid Division of urban power distribution[J]. Journal of state grid technology college, 2018, 21(1): 1-4. DOI:10.3969/j.issn.1008-3162.2018.01.001 (  0) 0) |
| [8] |
刘旭, 贺子尧. 利用网格化规划配电网建设[J]. 农村电气化, 2019(8): 79. LIU X, HE Z Y. Planning power distribution networks construction making use of gridding[J]. Rural electrification, 2019(8): 79. (  0) 0) |
| [9] |
国家电网. 配电网规划设计技术导则: Q/GDW 1738-2012[S]. 北京: 中国电力出版社, 2012: 3-4. STATE GRID. The guide of planning and design of distribution network: Q/GDW 1738-2012[S]. Beijing: China Electric Power Press, 2012: 3-4. (  0) 0) |
| [10] |
黄庆键, 欧周, 林佳亮. 关于空间电力负荷预测方法综述与展望[J]. 自动化应用, 2017(2): 79-81. HUANG Q J, OU Z, LIN J L. Review and prospect of spatial power load forecasting methods[J]. Automation application, 2017(2): 79-81. (  0) 0) |
| [11] |
肖白, 杨欣桐, 田莉, 等. 计及元胞发展程度的空间负荷预测方法[J]. 电力系统自动化, 2018, 42(1): 61-67. XIAO B, YANG X T, TIAN L, et al. Spatial load forecasting method based on development degree of cell[J]. Automation of electric power systems, 2018, 42(1): 61-67. (  0) 0) |
| [12] |
张明理, 宋卓然, 梁毅, 等. 基于饱和负荷密度的城市远景空间负荷预测[J]. 沈阳工业大学学报, 2018, 40(1): 12-18. ZHANG M L, SONG Z R, LIANG Y, et al. Forecasting for urban prospective spatial load based on saturated load density[J]. Journal of Shenyang university of technology, 2018, 40(1): 12-18. (  0) 0) |
| [13] |
中国城市规划设计研究院. 城市电力规划规范: GB/T 50293-2014[S]. 北京: 中国建筑工业出版社, 2014: 32-33. China academy of urban planning and design. Code for planning of urban electric power: GB/T 50293-2014[S]. Beijing: China Architecture and Building Press, 2014: 32-33. (  0) 0) |
| [14] |
张静, 王主丁, 张代红, 等. 配电网规划中负荷预测实际问题探讨[J]. 华东电力, 2014, 42(2): 384-390. ZHANG J, WANG Z D, ZHANG D H, et al. Actual load forecasting problems in distribution network planning[J]. East China electric power, 2014, 42(2): 384-390. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


