在斜拉桥的有限元模型中, 拉索的模拟是决定分析精度的重要因素.对于成桥阶段, 可以采用桁架单元, 用直杆模拟拉索.为增加分析的准确性, 可采用Ernst公式修正杆的弹性模量.对大跨度斜拉桥中大垂度的长索及施工过程中的拉索, 必须考虑索的曲线特性.为精确模拟曲线形索, 文献[1]建立了多节点的曲线单元, 文献[2]采用三次多项式插值建立了两节点的曲线单元, 文献[3]采用拉格朗日插值构造了两节点的曲线索单元, 文献[4]建立了五节点的曲线索单元.文献[5-7]利用弹性悬链线的解析解建立了弹性悬链线单元, 并建议了计算时的初值.目前, 弹性悬链线单元已被广泛应用于拉索模拟, 并被引入部分结构有限元分析软件(如Midas/Civil).文献[8]在该单元的基础上建立了分析索结构中滑动索的滑移索单元.文献[9]对单索问题进行了分类, 算例结果表明, 修正弹性模量的方法只能用于水平长度不超过400 m的斜拉索, 否则将引起较大的误差.文献[10-11]建立了带刚臂的索单元, 假定两端刚臂总与索端部相切, 在应用于斜拉桥模拟时, 限制了塔上节点的划分, 也不便与主梁连接.文献[12-13]也建立了带刚臂的索单元, 刚臂与索端部铰接, 且文献[13]指出文献[12]在对刚臂端部力矢量微分时, 忽略了对角度变量的微分.本文在弹性悬链线解析解的基础上建立了两端有弹性段的索单元, 进而在索单元两端增加刚臂, 推导和构造了该组合索单元.
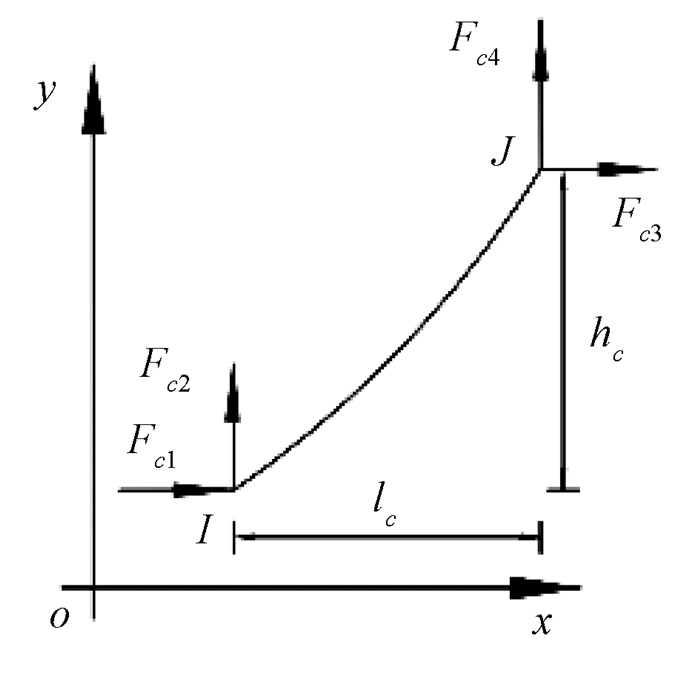
1 弹性悬链线单元一个弹性悬链线单元如图 1所示, 其水平投影长度为lc, 竖直投影长度为hc.索的弹性模量为E, 横截面面积为A0, 单位长度重量为q0, 该索段的无应力长度为L0.据弹性悬链线理论[6-7], 索的投影方程为
|
图 1 弹性悬链线单元 Fig. 1 Element of elastic catenary |
| $ {l_c} = - \frac{{{F_{c1}} \cdot {L_0}}}{{E \cdot {A_0}}} - \frac{{{F_{c1}}}}{{{q_0}}} \cdot \ln \left( {\frac{{{T_{Jc}} + {F_{c4}}}}{{{T_{Ic}} - {F_{c2}}}}} \right), $ | (1) |
| $ {h_c} = \frac{{{L_0}}}{{E \cdot {A_0}}} \cdot \left( {\frac{{{q_0} \cdot {L_0}}}{2} - {F_{c2}}} \right) + \frac{{{T_{Jc}} - {T_{Ic}}}}{{{q_0}}}, $ | (2) |
式中:TIc和TJc分别为索段左端和右端节点处的索力.
根据单元受力平衡条件, 可得Fc3=-Fc1, Fc4=q0·L0-Fc2.
式(1)和式(2)分别对Fc1、Fc2求偏导, 可得索段在I端的柔度矩阵为
| $ {\mathit{\boldsymbol{f}}_c} = \left[ {\begin{array}{*{20}{c}} { - {f_{c11}}}&{ - {f_{c12}}}\\ { - {f_{c21}}}&{ - {f_{c22}}} \end{array}} \right], $ | (3) |
其中:
左端点力的增大会使水平投影和竖直投影减小.因此, 柔度矩阵fc中各元素取计算值的负值.进而, 可得到弹性悬链线单元的刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_c} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_c}}&{ - {\mathit{\boldsymbol{k}}_c}}\\ { - {\mathit{\boldsymbol{k}}_c}}&{{\mathit{\boldsymbol{k}}_c}} \end{array}} \right], $ | (4) |
式中:kc为柔度矩阵fc的逆矩阵.
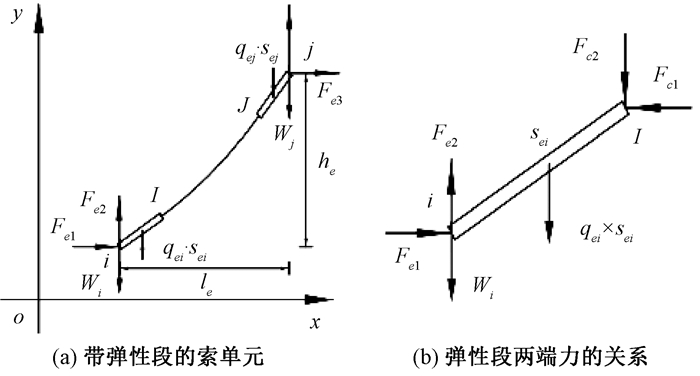
2 带弹性段的索单元索体两端的钢套筒与其内部的钢丝通过高强黏结材料固结为整体, 且钢套筒的横截面面积与其内部所有钢丝的横截面面积相当.因此, 套筒段宜单独考虑, 可近似为一个弹性段, 其方向沿索段端部索力方向, 也就是索段端部的切线方向.带弹性段的索单元如图 2(a)所示, 其水平投影长度为le, 竖直投影长度为he, Wi和Wj分别为索体端部超出锚垫板的锚杯部分和螺母的重量, sei、qei和sej、qej分别为两个弹性段的原长及单位长度重量, 弹性段受到的重力平移到相应的端部节点.
|
图 2 带弹性段的索单元和弹性段两端力的关系 Fig. 2 Cable element with elastic segments and forces on the both sides |
弹性段两端力的关系如由图 2(b)所示, 带弹性段的索单元的节点力为
| $ \left( {\begin{array}{*{20}{c}} {{F_{e1}}}\\ {{F_{e2}}}\\ {{F_{e3}}}\\ {{F_{e4}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{F_{c1}}}\\ {{F_{c2}} + {q_{ei}} \cdot {s_{ei}} + {W_i}}\\ {{F_{c3}}}\\ {{F_{c4}} + {q_{ej}} \cdot {s_{ej}} + {W_j}} \end{array}} \right). $ | (5) |
两端带弹性段索体的投影方程为
| $ {l_e} = {l_c} + {s_{ei}} \cdot \left( {\frac{{{T_{Ic}}}}{{{E_{ei}} \cdot {A_{ei}}}} + 1} \right) \cdot \frac{{ - {F_{c1}}}}{{{T_{Ic}}}} + {s_{ej}} \cdot \left( {\frac{{{T_{Jc}}}}{{{E_{ej}} \cdot {A_{ej}}}} + 1} \right) \cdot \frac{{ - {F_{c1}}}}{{{T_{Jc}}}}, $ | (6) |
| $ {h_e} = {h_c} + {s_{ei}} \cdot \left( {\frac{{{T_{Ic}}}}{{{E_{ei}} \cdot {A_{ei}}}} + 1} \right) \cdot \frac{{ - {F_{c2}}}}{{{T_{Ic}}}} + {s_{ej}} \cdot \left( {\frac{{{T_{Jc}}}}{{{E_{ej}} \cdot {A_{ej}}}} + 1} \right) \cdot \frac{{{q_0} \cdot {L_0} - {F_{c2}}}}{{{T_{Jc}}}}, $ | (7) |
式中:Eei和Aei分别为i端弹性段的弹性模量和横截面面积; Eej和Aej分别为j端弹性段的弹性模量和横截面面积.
式(6)和式(7)分别对Fc1、Fc2求偏导, 可得带弹性段的索单元在左端点的柔度矩阵为
| $ {\mathit{\boldsymbol{f}}_e} = \left[ {\begin{array}{*{20}{c}} { - {f_{e11}}}&{ - {f_{e12}}}\\ { - {f_{e21}}}&{ - {f_{e22}}} \end{array}} \right], $ | (8) |
其中:
带弹性段的索单元在左端点的刚度矩阵为
| $ \mathit{\boldsymbol{K}} = \mathit{\boldsymbol{f}}_e^{ - 1}. $ | (9) |
由刚度矩阵的对称性可知, 两端带弹性段的索单元的刚度矩阵可以表示为
| $ {\mathit{\boldsymbol{K}}_e} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{K}}&{ - \mathit{\boldsymbol{K}}}\\ { - \mathit{\boldsymbol{K}}}&\mathit{\boldsymbol{K}} \end{array}} \right]. $ | (10) |
根据刚度矩阵的定义, 可得
| $ \left( {\begin{array}{*{20}{c}} {\Delta {F_{e1}}}\\ {\Delta {F_{e2}}}\\ {\Delta {F_{e3}}}\\ {\Delta {F_{e4}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{K}}&{ - \mathit{\boldsymbol{K}}}\\ { - \mathit{\boldsymbol{K}}}&\mathit{\boldsymbol{K}} \end{array}} \right] \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_i}}\\ {\Delta {y_i}}\\ {\Delta {x_j}}\\ {\Delta {y_j}} \end{array}} \right). $ | (11) |
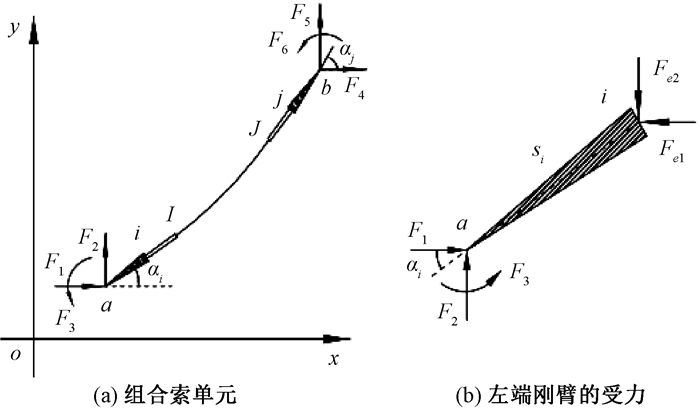
在带弹性段的索单元两端增加刚臂, 得到如图 3(a)所示的组合索单元.αi和αj分别为两端刚臂的倾角, 刚臂的长度分别为si和sj.左端刚臂的受力如图 3(b)所示, 其两端点之间的坐标关系[13]为
|
图 3 带刚臂和弹性段的组合索单元 Fig. 3 The combined cable element with rigid arms and elastic segments |
| $ {x_i} = {x_a} + {s_i} \cdot \cos {\alpha _i}, $ | (12) |
| $ {y_i} = {y_a} + {s_i} \cdot \sin {\alpha _i}. $ | (13) |
对式(12)和式(13)两端微分, 可得左端刚臂两端点之间的位移关系为
| $ \left( {\begin{array}{*{20}{c}} {\Delta {x_i}}\\ {\Delta {y_i}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0&{ - {s_i} \cdot \sin {\alpha _i}}\\ 0&1&{{s_i} \cdot \cos {\alpha _i}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_a}}\\ {\Delta {y_a}}\\ {\Delta {\alpha _i}} \end{array}} \right). $ | (14) |
同理, 可得右端刚臂两端点之间的位移关系为
| $ \left( {\begin{array}{*{20}{c}} {\Delta {x_j}}\\ {\Delta {y_j}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0&{{s_j} \cdot \sin {\alpha _j}}\\ 0&1&{ - {s_j} \cdot \cos {\alpha _j}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_b}}\\ {\Delta {y_b}}\\ {\Delta {\alpha _j}} \end{array}} \right). $ | (15) |
联立式(14)和式(15), 并记
| $ \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} 1&0&{ - {s_i} \cdot \sin {\alpha _i}}\\ 0&1&{{s_i} \cdot \cos {\alpha _i}} \end{array}} \right),\mathit{\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}} 1&0&{{s_j} \cdot \sin {\alpha _j}}\\ 0&1&{ - {s_j} \cdot \cos {\alpha _j}} \end{array}} \right), $ | (16) |
可得
| $ \left( {\begin{array}{*{20}{c}} {\Delta {x_i}}\\ {\Delta {y_i}}\\ {\Delta {x_j}}\\ {\Delta {y_j}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&\mathit{\boldsymbol{B}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_a}}\\ {\Delta {y_a}}\\ {\Delta {\alpha _i}}\\ {\Delta {x_b}}\\ {\Delta {y_b}}\\ {\Delta {\alpha _j}} \end{array}} \right). $ | (17) |
根据刚臂两端力的关系, 组合索单元的节点力可以表示为
| $ \left( {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}}\\ {{F_4}}\\ {{F_5}}\\ {{F_6}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {{F_{e1}}}\\ {{F_{e2}}}\\ {{s_i} \cdot \cos {\alpha _i} \cdot {F_{e2}} - {s_i} \cdot \sin {\alpha _i} \cdot {F_{e1}}}\\ {{F_{e3}}}\\ {{F_{e4}}}\\ { - {s_j} \cdot \cos {\alpha _j} \cdot {F_{e4}} + {s_j} \cdot \sin {\alpha _j} \cdot {F_{e3}}} \end{array}} \right]. $ | (18) |
对式(18)两端微分, 可得
| $ \left( {\begin{array}{*{20}{c}} {\Delta {F_1}}\\ {\Delta {F_2}}\\ {\Delta {F_3}}\\ {\Delta {F_4}}\\ {\Delta {F_5}}\\ {\Delta {F_6}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}}&0\\ 0&{{\mathit{\boldsymbol{B}}^{\rm{T}}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\Delta {F_{e1}}}\\ {\Delta {F_{e2}}}\\ {\Delta {F_{e3}}}\\ {\Delta {F_{e4}}} \end{array}} \right) + {\mathit{\boldsymbol{T}}_\alpha } \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_a}}\\ {\Delta {y_a}}\\ {\Delta {\alpha _i}}\\ {\Delta {x_b}}\\ {\Delta {y_b}}\\ {\Delta {\alpha _j}} \end{array}} \right), $ | (19) |
其中Tα除了两个元素Tα3, 3=-si·cos αi·Fe1-si·sin αi·Fe2, Tα6, 6=sj·cos αj·Fe3+sj·sin αj·Fe4外, 其余元素均为零.
联立式(11)、式(17)、式(19), 可得组合索单元的刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_E} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{A}}}&{ - {\mathit{\boldsymbol{A}}^{\rm{T}}} \cdot \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{B}}}\\ { - {\mathit{\boldsymbol{B}}^{\rm{T}}} \cdot \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{A}}}&{{\mathit{\boldsymbol{B}}^{\rm{T}}} \cdot \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{B}}} \end{array}} \right] + {\mathit{\boldsymbol{T}}_\alpha }. $ | (20) |
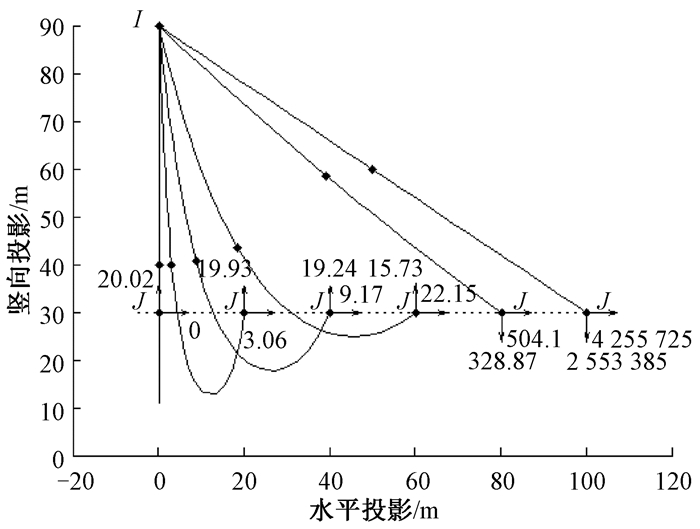
算例1 下端位于不同位置的单根索如图 4所示, 该索的计算参数见文献[5]和[11], 无应力长度L0=100 m, 横截面面积A0=1 cm2, 弹性模量E=3×107 Pa, 单位长度重量q0=1 N/m, 线膨胀系数为6.5×10-6.采用2个等原长的弹性悬链线单元模拟该索, 共有3个节点.
|
图 4 下端位于不同位置的单根索 Fig. 4 Single cable with the lower end at different locations |
由图 4可以看出, 不考虑弹性段的计算结果, 与文献[5]对比, 除最大张力工况有一定误差外, 其他结果相同.最大张力工况的计算结果与文献[11]的结果相同, 从而证明了本文弹性悬链线单元部分推导的正确性.
考虑弹性段时, 具体可分为以下两种情况:一种是弹性段的参数不变化; 另一种是弹性段的面积增加1倍, 单位长度索重增加1倍.算例1中弹性段在不同取值情况下的计算结果见表 1.结果表明, 第1种情况下的结果与不考虑弹性段的误差很小.第2种情况在索力较小的几个工况下, 只是竖向索力稍有增加, 但绝对量很小; 对于张力最大的工况, 水平索力和竖向索力都有较大增加, 这与实际情况相符, 表明在索力很大时, 不考虑弹性段会带来较大的误差.
|
|
表 1 算例1中弹性段在不同取值情况下的计算结果 Tab. 1 Results as the elastic segment taking different values in example 1 |
算例2 索段的弹性模量E=2×1011 Pa, 截面面积A0=10-5 m2, 单位长度重量q0=10 N/m, 无应力长度L0=3.604 842 m.左、右两端刚臂长均为0.8 m, 左端刚臂倾角αi=30°, 右端刚臂倾角αj=60°.两端的弹性段长度均为0.600 925 m, 与索段的弹性模量相等, 截面面积为10-6 m2, 各弹性段重量均为50 N, 弹性段外端各附加50 N的点荷载.弹性段截面面积取索的十分之一, 以便于弹性段有较大的变形.
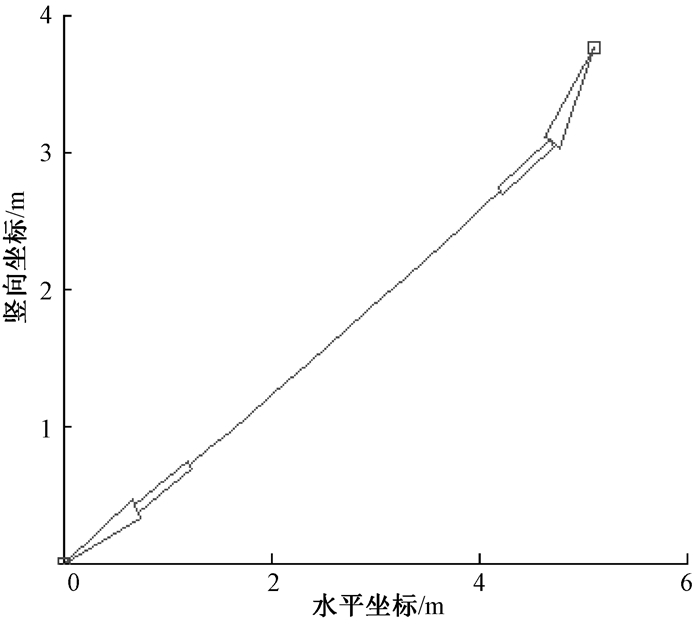
单元的左端点位于原点, 右端点位于(5.095 698 3, 3.761 006 7) m.算例2中组合单元在变形后的形状图见图 5, 组合索单元的节点力为(-500.045, -215.439, 50.757, 500.045, 451.488, 165.847) N.
|
图 5 算例2中组合单元在变形后的形状图 Fig. 5 The profile after displacement of the combined element in example 2 |
平衡状态下, 可推算出去除两端刚臂后, 带弹性段索单元的节点力为(-500.045, -215.439, 500.045, 451.488) N, 它们对左刚臂左端产生的力矩为-50.757 N·m, 与单元在左刚臂处的第3个节点力分量平衡, 右端也如此.推算索段两端的节点力为(-500.045, -315.439, 500.045, 351.488) N, 索段两端的水平投影长度为3 m, 竖直投影长度为2 m, 由式(1)和(2)可知, 索段处于平衡状态.因此, 组合索单元的单元节点力计算正确.通过依次使组合索单元的各自由度有一微小的位移增量, 计算得到单元节点力的增量, 可按定义法得到单元的刚度矩阵.经检验, 组合索单元输出的刚度矩阵与按定义法得到的刚度矩阵相同.因此, 根据推导所计算的刚度矩阵是完全正确的.
5 结论基于弹性悬链线的解析解, 首先建立了悬链线单元, 进而在两端增加弹性段, 推导了带弹性段的索单元的相关公式; 又在带弹性段的索单元两端增加刚臂, 构成了组合索单元, 算例证明了所推导公式及编程的正确性.本文的组合索单元是多功能的.在两端刚臂长度取零值的情况下, 可退化为只有单侧刚臂或不带刚臂的带弹性段索单元; 在弹性段长度取零值的情况下, 可退化为带刚臂而不带弹性段的单元; 当不考虑刚臂和弹性段后, 组合索单元可进一步退化为弹性悬链线单元.在已知索端部某个张力或张力分量的情况下, 可通过求解索段的水平投影与竖直投影方程得到索原长, 进而建立该组合单元.因此, 该组合索单元可用于模拟索的张拉过程.组合索单元可用于斜拉桥的设计与分析, 能更精确地模拟拉索, 也可以用于模拟拱桥中的吊杆和悬索桥中的吊索.
| [1] |
HENGHOLD W H, RUSSELL J J. Equilibrium and natural frequencies of cable structures(a nonlinear finite element approach)[J]. Computers and structures, 1976, 6(4): 267-271. (  0) 0) |
| [2] |
GAMBHIR M L, BATCHELOR B. A finite element for 3-D prestressed cablenets[J]. International journal for numerical methods in engineering, 1977, 11(11): 1699-1718. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [3] |
OZDEMIR H. A finite element approach for cable problems[J]. International journal of solids and structures, 1979, 15(5): 427-437. DOI:10.1016/0020-7683(79)90063-5 (  0) 0) |
| [4] |
唐建民, 董明, 钱若军. 张拉结构非线性分析的五节点等参单元[J]. 计算力学学报, 1997, 14(1): 108-113. (  0) 0) |
| [5] |
PEVROT A H, GOULOIS A M. Analysis of cable structures[J]. Computers and structures, 1979, 10(5): 805-813. DOI:10.1016/0045-7949(79)90044-0 (  0) 0) |
| [6] |
JAYARAMAN H B, KNUDSON W C. A curved element for the analysis of cable structures[J]. Computers and structures, 1981, 14(3/4): 325-333. (  0) 0) |
| [7] |
IRVINE H M. Cable structures[M]. Cambridge: the MIT Press, 1981.
(  0) 0) |
| [8] |
魏建东. 索结构分析的滑移索单元法[J]. 工程力学, 2004, 21(6): 172-176. DOI:10.3969/j.issn.1000-4750.2004.06.028 (  0) 0) |
| [9] |
梁鹏, 徐岳, 刘永健. 斜拉索分析统一理论及其应用[J]. 建筑科学与工程学报, 2006, 23(1): 68-77. DOI:10.3321/j.issn:1673-2049.2006.01.013 (  0) 0) |
| [10] |
罗喜恒, 肖汝城, 项海帆. 基于精确解析解的索单元[J]. 同济大学学报(自然科学版), 2005, 33(4): 445-450. DOI:10.3321/j.issn:0253-374X.2005.04.005 (  0) 0) |
| [11] |
YANG Y B, TSAY J Y. Two-node catenary cable element with rigid-end effect and cable shape analysis[J]. International journal of structural stability and dynamics, 2011, 11(3): 563-580. DOI:10.1142/S021945541100421X (  0) 0) |
| [12] |
陈常松, 颜东煌, 陈政清. 带刚臂的两节点精确悬链线索元的非线性分析[J]. 工程力学, 2007, 24(5): 29-34. DOI:10.3969/j.issn.1000-4750.2007.05.005 (  0) 0) |
| [13] |
邓继华, 谭平, 彭建新. 带刚臂平面悬链线索单元的非线性分析[J]. 应用力学学报, 2014, 31(3): 348-352. (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


