随着科技的发展,人们对于信息的安全也越来越重视.隐写术和密码学是信息安全的两大技术,各有不同的应用范围,将两者相结合,能够有效地提高信息的安全性.
汉明码由于编码简单,因此得到广泛的应用.近年来,人们对边缘检测和汉明码的研究已经取得了一些显著成果.文献[1]提出了一种基于Canny边缘检测的自适应空域检测算法,该算法对常见的隐写分析方法具有鲁棒性.文献[2]提出了基于2k修正和霍夫曼编码的图像隐写,该方法能够有效地增强隐写图像的视觉效果.文献[3]提出的算法既具有很高的隐藏能力,又具有很好的隐藏效率.文献[4]提出了使用(7, 4)汉明码对压缩图像进行信息隐藏,把信息隐藏在使用动量绝对值区块截短码进行压缩的图像中.文献[5]提出了使用(15, 11)汉明码在半色调图像中进行信息隐藏的方法.
1 Logistic-正弦映射 1.1 Logistic映射Logistic映射是最简单常用的一维混沌映射.表达式为xn+1=L(μ, xn)=μxn(1-xn),参数μ的取值范围是[3.57, 4].但在这个区间内,也并不是所有值都能使系统处于混沌状态.Logistic映射的李雅普诺夫指数较小,而且生成的混沌序列分布并不均匀,这些都是Logistic映射存在的不足之处.
1.2 正弦映射| $ {x_{n + 1}} = S(\mu, {x_n}) = \mu \;{\rm{sin}}(\pi {x_n})/4, $ | (1) |
当式(1)的参数μ在[3.48, 4]范围内,正弦映射系统处于混沌状态.其混沌特性与Logistic映射类似,同Logistic映射一样,具有有限的参数范围和生成的混沌序列分布不均匀的缺点.
1.3 Logistic-正弦映射| $ {x_{n + 1}} = (L(\mu, {x_n}) + S(\left( {4-\mu } \right), {x_n})){\rm{mod}}\;1 \\= (\mu {x_n}(1-{x_n}) + \left( {4-\mu } \right){\rm{sin}}({\rm{ \mathsf{ π} }}{x_n})/4){\rm{mod}}\;1, $ | (2) |
当式(2)的参数μ在(0, 4]范围内,系统处于混沌状态.与Logistic映射和正弦映射相比,Logistic-正弦映射具有更大的参数空间,混沌序列分布得更加均匀,同时具有更大的李雅普诺夫指数[6],因此更适合混沌图像加密的需要.
2 汉明码汉明码是由Richard Hamming[7]提出的,它是一种能够检测并修正误差的块码.在所有汉明码中,(7, 4)汉明码的应用最为广泛.它把4 bit的数据位(m1, m2, m3, m4)与3 bit的校验位(p1, p2, p3)组合在一起成为7 bit的码字.每一bit的校验位是由相应的数据位决定的.汉明码是通过校验位与相应的数据位是否形成偶校验来检测是否存在误差的[8].检测过程又称为校验,所用公式为
| $ {2^r}-1 \ge n\;或者\;{2^r}-1 \ge k + r, $ | (3) |
其中:n是码字的长度;k是数据位的长度;r是校验位的长度,r≥2.
表 1显示了数据位和校验位之间的关系,这里“√”表示相应的校验位和数据位之间存在关系.m1、m2、m3和m4是数据位,p1、p2和p3是校验位.
|
|
表 1 校验位与数据位之间的关系 Table 1 Relationship between parity bit and data bit |
校验位能用相应的数据位产生,
| $ {p_1} = {m_1} \oplus {m_2} \oplus {m_4}, {p_2} = {m_1} \oplus {m_3} \oplus {m_4}, {p_3} = {m_2} \oplus {m_3} \oplus {m_4}, $ |
“⊕”表示异或操作.
对于(7, 4)汉明码来说,相应的数据位和校验位的关系如表 2所示.
|
|
表 2 (7, 4)汉明码的码字 Table 2 Codewords of (7, 4) Hamming code |
把数据位与校验位组合在一起形成码字的方法是把校验位放在2i位置上,例如p1p2m1p3m2m3m4.
在使用汉明码进行编码的时候,需要用到校验矩阵H和产生矩阵G.矩阵G用来编码,矩阵H用来校验数据.在发送端,每4 bit数据乘以编码矩阵G,并把结果对2求模,得到码字R,所用公式为
| $\mathit{\boldsymbol{R}} = \left( {\mathit{\boldsymbol{M}} \times \mathit{\boldsymbol{G}}} \right){\rm{mod}}\;2, $ | (4) |
其中:M=(m1, m2, m3, m4);
| $ \mathit{\boldsymbol{G}}{\rm{ = }}\left[{\begin{array}{*{20}{c}} 1&1&1&0&0&0&0\\ 1&0&0&1&1&0&0\\ 0&1&0&1&0&1&0\\ 1&1&0&1&0&0&1 \end{array}} \right]. $ |
在接收端,为了校验收到的7 bit码字R(数据位加上校验位)是否正确,将向量R乘以校验矩阵H的转置矩阵,结果对2求模,如式
| $ \mathit{\boldsymbol{Z}} = (\mathit{\boldsymbol{R}} \times {\mathit{\boldsymbol{H}}^{\rm{T}}})\;{\rm{mod}}\;2, $ | (5) |
其中:
| $ \mathit{\boldsymbol{H}}{\rm{ = }}\left[{\begin{array}{*{20}{c}} 1&0&1&0&1&0&1\\ 0&1&1&0&0&1&1\\ 0&0&0&1&1&1&1 \end{array}} \right]; $ |
向量Z由3 bit向量(z1, z2, z3)组成.如果消息传输正确,则向量Z为0,即(0, 0, 0).否则,相应的位变为1,那么该消息就需要进行错误检测.
3 秘密信息隐藏算法信息隐藏的过程如图 1所示.具体算法步骤如下:
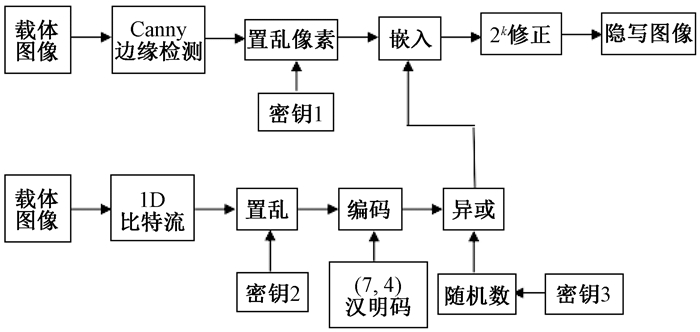
|
图 1 信息隐藏过程框图 Figure 1 Diagram of data hiding process |
1) 读取载体图像和密码图像.
2) 用Canny边缘检测算子检测载体图像边缘.
3) 用Logistic-正弦映射产生密钥1、密钥2和密钥3.
4) 用密钥1置乱边界像素.
5) 秘密图像转换为1D比特流.
6) 用密钥2置乱1D比特流.
7) 用(7, 4)汉明码编码1D比特流,并与用密钥3产生的随机数进行异或操作.
8) 比特流嵌入置乱后的边缘像素.
9) 用2k修正算法提高图像的视觉效果.
10)最终获得隐写图像.
信息提取的过程是上述过程的逆过程.
4 实验过程和结果本文的实验是在Windows 7下用Matlab 10实现的.为了衡量提出算法的效果,采用峰值信噪比(PSNR)、结构化的图像质量评价方法[9]和隐藏能力来度量.
为了计算PSNR,首先要计算均方误差(MSE),公式为
| $ MSE = \frac{1}{{MN}}\sum\limits_{i = 0}^{M-1} {\sum\limits_{j = 0}^{N-1} {{{\left\| {\mathit{\boldsymbol{I}}\left( {i, j} \right)-\mathit{\boldsymbol{S}}\left( {i, j} \right)} \right\|}^2}} }, $ |
其中:I是载体图像;S是隐写图像;M和N是载体图像的大小.PSNR值计算公式为
| $ PSNR = 20\;{\rm{lo}}{{\rm{g}}_{10}}\left( {\frac{{255}}{{\sqrt {MSE} }}} \right). $ | (6) |
结构化的图像质量评价方法为
| $ \bar x = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} ;{\rm{ }} = \frac{1}{N}\sum\limits_{i = 1}^N {{y_i}} ;{\rm{ }}x = \{ {x_i}\left| {i = 1,{\rm{ }}2, \ldots ,{\rm{ }}N} \right.\} ;{\rm{ }}y = \{ {y_i}\left| {i = 1,{\rm{ }}2, \ldots ,{\rm{ }}N} \right.\} ; $ |
| $ {\sigma _x}^2 = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{({x_i} - \bar x)}^2}} ;{\sigma _y}^2 = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{({y_i} - \bar y)}^2}} ;\\{\sigma _{xy}} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {({x_i} - \bar x)({y_i} - \bar y)} . $ |
信息隐藏能力Capacity用每个像素能够隐藏的bit数来表示.本文所提出的方法与文献[10]以及最低3位有效位方法(LSB-3)进行比较.载体图像大小是512×512的灰度图像,秘密图像大小是128×128的灰度图像.图 2显示了应用Canny检测算子得出的载体图像的边缘.高斯滤波器的标准差为1.5,低门限设定为5,高门限设为40.本文把秘密信息隐藏在3种方法的边缘像素中.尽管负载较其他方法小,但是PSNR和Q值较大.从表 3可见,本文的方法比LSB-3和文献[10]的方法更好.

|
图 2 Canny算子检测的载体边缘 Figure 2 Edge images with Canny detector |
|
|
表 3 三种参数的比较 Table 3 Comparison of three parameters |
图 3显示了载体图像、隐写图像及其对应的直方图,同时显示出秘密图像及其提取的秘密图像.
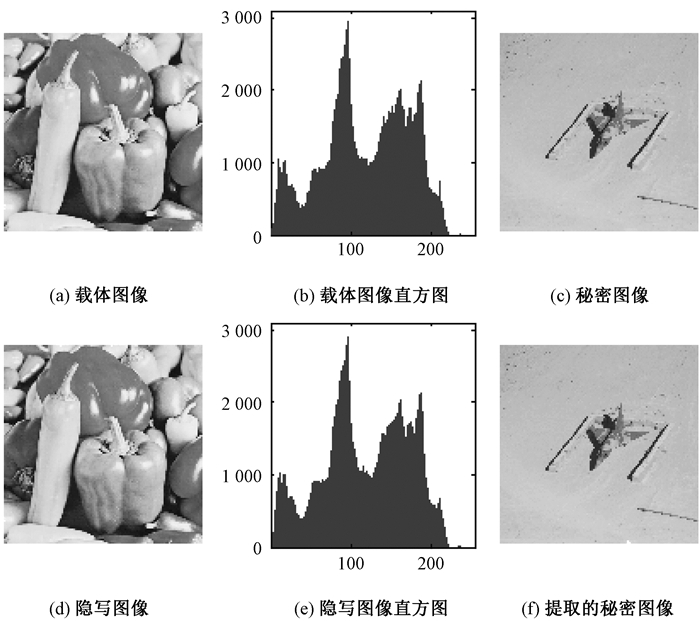
|
图 3 隐写图像和提取的秘密图像 Figure 3 Stego image and retrieved image |
本文提出了基于Logistic-正弦映射和汉明码的新型信息隐藏算法.由于人眼对平滑区域比对边缘区域更加敏感,因此秘密信息仅仅隐藏在载体的边缘像素中.用汉明码对秘密信息进行编码.利用Logistic-正弦映射生成3个密钥,最后用2k修正法提高隐写图像的视觉效果.实验证明本文提出的算法具有更好的安全性、有效性和鲁棒性.
| [1] |
韩涛, 祝跃飞. 基于Canny边缘检测的自适应空域隐写术[J]. 电子与信息学报, 2015, 37(5): 1266-1270. DOI:10.11999/JEIT141121 (  0) 0) |
| [2] |
SUN S L. A novel edge based image steganography with 2k correction and Huffman encoding[J]. Information processing letters, 2016, 116(2): 93-99. DOI:10.1016/j.ipl.2015.09.016 (  0) 0) |
| [3] |
ZHANG Y, JIANG J, ZHA Y, et al. Research on embedding capacity and efficiency of information hiding based on digital images[J]. International journal of intelligence science, 2013, 3(2): 77-85. DOI:10.4236/ijis.2013.32009 (  0) 0) |
| [4] |
BAI J, CHANG C C. A high payload steganographic scheme for compressed images with hamming code[J]. International journal of network security, 2016, 18(6): 1122-1129. (  0) 0) |
| [5] |
KIM C, SHIN D, SHIN D. Intelligent Information and Database Systems[M]. Heidelberg: Springer, 2011.
(  0) 0) |
| [6] |
ZHOU Y, BAO L, CHEN C L P. A new 1D chaotic system for image encryption[J]. Signal processing, 2014, 97(7): 172-182. (  0) 0) |
| [7] |
HAMMING R W. Error detecting and error correcting codes[J]. Bell system technical journal, 2014, 29(2): 147-160. (  0) 0) |
| [8] |
朱雪秀, 刘九芬, 张卫明. 一种基于汉明码和湿纸码的隐写算法[J]. 电子与信息学报, 2010, 32(1): 162-165. (  0) 0) |
| [9] |
WANG Z, BOVIK A C. A universal image quality index[J]. IEEE signal processing letters, 2002, 9(3): 81-84. DOI:10.1109/97.995823 (  0) 0) |
| [10] |
YU J G, YOON E J, SHIN S H, et al. A new image steganography based on 2k correction and edge-detection [C]// Information Technology: New Generations. New York, 2008: 563-568.
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


