作为描述多属性之间定性条件偏好的图模型, CP-nets[1]的理论研究已经成为人工智能领域的一大热点问题[2], 其中CP-nets结构学习问题研究起着至关重要的作用。并行算法是在并行机上利用很多个处理器联合求解问题和处理数据。作为一种处理大规模数据的分布式计算系统, Hadoop具有优秀的可移植性, 其核心是由NameNode分布式文件系统和MapReduce分布式计算框架组成, 解决了大规模数据的存储和算法的并行设计问题。目前, 国内对CP-nets结构学习的主要思想是在属性验证基础上穷举每个属性的可行父亲集[3], 得到的都是CP-nets的近似结构。不同于传统的CP-nets结构学习方法, 本文设计了一种基于MapReduce框架的相关系数并行算法, 首次将传统的“评分+搜索”方法[4]应用到Hadoop平台上, 利用信息论中的相关系数建立在偏好数据库上的目标函数, 提高属性间的依赖性和降低冗余性; 在电影推荐数据集上分析用户对电影的评分, 找出用户和电影之间的相互关系, 快速高效地从大规模数据中进行CP-nets结构学习。
1 相关工作近年来对CP-nets结构学习的研究方法众多, 然而由于结构的多样性, 进行学习是非常困难的。文献[5]基于精确P值计算学习CP-nets的拓扑结构, 首先选择一个顶点Xi, Xi的可行父亲集是全集V减去顶点Xi之后剩余集合中的任意子集组合, 根据Dijkstra原理比较每个顶点与其对应的可行父亲集之间的P值, 循环学习得到CP-nets的无环结构, 但存在时间复杂度不乐观等诸多问题。文献[6]为了学习CP-nets结构, 利用假设检验方法从噪声数据中进行学习, 但仅仅给出了全序关系下的CP-nets结构学习方法。对CP-nets结构学习的已有研究都是在基于关系数据库基础上进行的, 并不具有代表性。在此背景下, 本文提出了一种从偏好数据库中学习CP-nets结构的并行算法。
在机器学习领域, “评分+搜索”是目前使用较为广泛的图模型结构学习方法。这类方法将CP-nets结构学习问题看作是结构最优化问题, 包括了评分函数和搜索空间两部分。评分函数可以灵活地将专家经验知识以结构先验概率分布的形式融入结构学习过程中, 主要分为贝叶斯评分函数和基于信息论的评分函数。搜索空间包括序空间搜索和基于DAG的空间搜索, 其中序空间搜索依靠动态规划法来实现。本文考虑到属性之间的相关性、冗余性和算法的执行效率, 提出了一种利用相关系数评分函数[7]和序空间搜索从偏好数据库中学习CP-nets结构的算法, 并行地对偏好数据库进行数据挖掘, 利用评分函数表达属性间的依赖关系, 序空间搜索在改变属性间边的情况下求得属性间依赖冗余关系, 可以从不同类型的电影推荐数据集中挖掘出偏好依赖关系, 该算法基于MapReduce框架进行设计, 在处理大规模数据时展现出了良好的性能。
2 CP-nets结构学习相关概念 2.1 CP-nets如果两个属性之间存在依赖关系, 即属性Xi的偏好取决于Xj, 则Xj被称为Xi的父亲, 用Pare(Xi)表示; Dom(Xi)表示属性Xi的定义域; CPT(Xi)表示可行父亲集Pare(Xi)在不同情况下属性Xi对Dom(Xi)的偏好排序。
定义1[1] (条件偏好网) CP-nets是一个用N=〈V, CE, CPT〉表示的有向图, 其中:V={X1, X2, …, Xn}表示CP-nets所有属性的顶点集合; CE={(Xi, Xj)|Xj∈Pare(Xi), Xi∈V}为CP-nets结构中有向边的集合, 表示各个顶点属性之间的依赖关系; 每个属性Xi对应于一个用来表示偏好关系的条件偏好表CPT(Xi)。
2.2 偏好数据库定义2(偏好数据库) 设P(a1, a2, …, an)是一个关系模式, Tuple(P)表示属于P的所有元组, Tuple(P)上的偏序集合B=Tuple(P)×Tuple(P)称为偏好数据库。例如, (o1, o2)∈B被称为一个二元组, 表示比较偏好数据库B里的o1与o2, 如果更偏好于o1, 则用o1>o2表示[8]。
定义3(划分属性) 设偏好数据库B, 属性为X, 则在偏好数据库B中关于X的划分属性为
| $ \begin{array}{l} \mathit{Divide}(X) = \left\{ {\left( {{x_i}, {x_j}} \right)|\left( {o\left[ {{x_i}} \right] = {x_1}, o\left[ {{x_j}} \right] = {x_2} \cup o\left[ {{x_i}} \right] = {x_2}, o\left[ {{x_j}} \right] = {x_1}} \right)} \right., \\ \left. {\left( {{o_i}, {o_j}} \right) \in B, \left( {{x_i}, {x_j}} \right) \in \mathit{Dom}(X)} \right\}, \end{array} $ | (1) |
式中:o[xi]表示xi在偏好数据库B上的映射; Dom(X)表示属性X的定义域。
2.3 “评分+搜索”方法“评分+搜索”方法学习CP-nets结构的主要思想, 是利用某种评分思路对CP-nets的每个组合(顶点及其他的可行父亲集)构造一个评分, 然后在所有可能的结构中, 搜索寻找一组全局最优的结构。“评分+搜索”方法众多, 本文采用特征选择中的相关系数评分函数学习CP-nets结构。统计学中使用协方差来度量两个属性之间的总体误差, 随机变量X和Y之间的协方差表示为
| $ \mathit{cov}\left( {\sum\limits_{i = 1}^n {{X_i}} , \sum\limits_{j = 1}^m {{Y_j}} } \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\mathit{cov}} } \left( {{X_i}, {Y_j}} \right)。$ | (2) |
方差用于衡量随机变量与其数学期望之间的偏离程度, 随机离散变量X的方差表示为
| $ \begin{array}{l} \mathit{var}(X) = \sum\limits_{i = 1}^n {\mathit{var}} \left( {{X_i}} \right) + 2\sum\limits_{i < j} {\mathit{cov}} \left( {{X_i}, {X_j}} \right) = \frac{{\sum\limits_{{\alpha _i} \in \mathit{Divide}\left( {{X_i}} \right)} {\sum\limits_{i = 1}^n {\left( {{X_i} - {\alpha _i}} \right)} } \left( {{X_i} - {\alpha _i}} \right)}}{{n - 1}} + \\ 2 \times \frac{{\sum\limits_{{\alpha _i}, {\beta _j} \in {\rm{ }}\mathit{Divide}(X)} {\sum\limits_{j = 1, i < j}^n {\left( {{X_i} - {\alpha _i}} \right)} } \left( {{X_i} - {\alpha _i}} \right)}}{{n - 1}} \times \frac{{\sum\limits_{{\alpha _i}, {\beta _j} \in {\rm{ }}\mathit{Divide}(X)} {\sum\limits_{j = 1, i < j}^n {\left( {{X_j} - {\beta _j}} \right)} } \left( {{X_j} - {\beta _j}} \right)}}{{n - 1}}, \end{array} $ | (3) |
式中:α、β表示当前偏好数据库中, 通过划分属性计算具有相同属性偏好的个数。
2.3.1 评分函数定义4 (相关性评分函数) 使用线性相关系数来衡量属性之间的线性相关度, 表示为
| $ \max R(X, Y) = \sum\limits_{i = 1}^n {\sum\limits_{{X_i} \in V} {\frac{{\mathit{cov}\left( {{X_i}, Y} \right)}}{{\sqrt {\mathit{var}\left( {{X_i}} \right)\mathit{var}(Y)} }}} } + |V|\frac{{\log _2^n}}{2}, $ | (4) |
式中:|V|表示初始特征子集中成对比较的个数; cov(Xi, Y)表示属性Xi和属性Y之间的协方差; var(Y)表示属性Y的方差。好的评分函数具有可分解性、易解性等优秀特征, 其中可分解性可以帮助算法进行搜索, 允许其独立于其他因素的影响。
2.3.2 搜索空间属性之间的父亲关系, 从全集到空集可以构成n!条不同的序搜索路径, 同样的一条路径对应一个CP-nets可行结构[9]。假设最优路径为{A, B, C, D, E}→{A, B, C, D}→{A, B, C}→{A, B}→{A}→Ø, 代表最优路径为A, B, C, D, E, 从而也得到了CP-nets的最优路径结构。
3 基于MapReduce的算法设计作为MapReduce最流行的开源实现, Hadoop使用块级调度和排序合并技术来实现并行处理的分组功能[10]。本文提出的基于MapReduce的“评分+搜索”的相关系数算法, 可以把原来庞大且无序的电影推荐数据集进行数据规整, 并从中提取来自不同类型电影的评论热点, 从而得到用户对电影的不同偏好, 进而为电影的生产者、销售者与消费者提供建议。
算法的基本思想是根据原始数据集M生成对应的初始特征子集V, 分别在节点上求取每个特征子集之间的依赖关系, 对给定的所有候选父亲结构并行地进行统计, 对CP-nets结构中每个节点的候选结构进行评分, 选取候选结构中相关系数评分最高的局部最优结构, 将具有最高评分的候选结构作为下一次搜索的基础迭代进行, 直至选取到最高的评分, 继而得到全局最优结构。算法1的具体步骤如下。
算法1 Learn_CP-netsstructure
输入: M, V, R(), U;
输出: CP-nets N, N=〈V, CE, CPT(X)X∈V〉;
Step 1 CE=Ø;FirstS=R(X, U); //FirstS表示对初始特征子集V中U的初始评分, U为V中的各个顶点。
Step 2 Foreach Xi∈V do
NowS=maxR(Xi, U);
//依据偏好数据库中数据集的数据, 通过式(1)可知, 划分属性代表了属性X在偏好数据库中有限定义域的排列组合, 计算划分属性, 继而并行计算相关性系数评分, 得到各顶点之间的依赖关系(伪代码步骤见算法2)。
Step 3 If FirstS < NowS
then NowS=FirstS; CE=CE∪(Xi, Pare(Xi));
else FirstS=NowS; CE=CE∪(Xi, Pare(Xi));
End for
Step 4 N=〈V, CE, CPT(X)X∈V〉;
Return N;
局部评分Map阶段, 利用数据处理阶段生成的候选结构D及其对应的CPT, 动态分配到多个Map任务当中, 每个Map任务调用Map函数对其进行评分, 将结果以对应的子节点为键, 候选结构、CPT以及打分结果为该节点所对应的值, 将结果输出至Reduce函数。Reduce阶段接收Map阶段的输出, 首先查找到具有相同子节点中评分最高的一项候选结构作为局部最优结构并输出, 将对应于该项的候选结构作为key值, 相对应的CPT作为value值进行输出。伪代码在算法2中进行详细描述。
算法2 Compute_Score
输入: Map(String key, String value); 候选结构〈D, max R()〉及其对应的CPT;
输出: 〈各节点最优结构, CPT〉;
//key为一个候选结构, value为候选结构进行相关性评分函数max R()设置参数。
Foreach Xi∈V do
Node=Dom(key); //Node为key所对应的候选结构的子节点;
S=max R(key, value); //依据key和value的值调用评分函数求取相应的评分S。
End for
Return 〈Node, 〈key, S, CPT〉〉;
输入: Reduce (String key, iterator values); 候选结构〈Node, 〈key, S, CPT〉〉及其对应的CPT;
输出: 〈各节点最优结构, CPT〉;
//key为候选结构对应的子节点, iterator values包含该子节点中对应的候选结构、评分数值和相应的CPT。
Foreach value do
search max(value.S); //找寻每一子节点中最大评分函数所对应的项。
End for
Return 〈value.key, value.CPT〉;
基于MapReduce的“评分+搜索”方法对CP-nets结构并行学习, 首先并行从数据集学习得到的评分函数中所需要的参数, 在对候选结构并行评分过程中利用已得到的参数, 对全部节点的候选父亲结构并行地完成相关系数评分, 最终得到各节点的局部最优结构以及对应属性的CPT, 通过简单合并得到全局最优CP-nets结构和对应结构的CPT, 即完成对CP-nets结构的并行学习[10]。
4 实验结果分析在两类电影数据集上进行实验验证:一类是由电影公司Netflix提供的电影推荐数据集, 该数据集包含480 189个用户、17 770部电影、100 480 507条评分记录, 包括动作片、冒险片等18种类型的电影; 另一类是由GroupLens Research收集的MovieLens网站, 包括了943个用户对1 682部电影的1 000 000条评分记录。每一种类型的电影都可以看作是CP-nets的一个属性。
为了验证算法的性能, 将学习得到的CP-nets N与原模型CP-nets N0的主要要素进行对比, 评价标准使用图模型结构相似度和加速比。
4.1 相似度分析CP-nets学习包括参数和结构学习, 本文着重关注结构学习, 选择相似度作为评价结构学习结果的标准。相似度是指学习得到的CP-nets N与原模型CP-nets N0之间的结构相似性。由于CP-nets是描述偏好关系的图模型, 很难判断图模型之间的相似性。因此, 可以将结构相似度转换为边的相似度, 用边的相似度来描述结构的相似度。相似度越高, 算法的性能越好。边的相似度公式表示为
| $ \mathit{Similarit}{\mathit{y}_{\mathit{edge}}} = \frac{{\mathit{num}\left( {\mathit{agre}{\mathit{e}_ - }\mathit{edge}} \right)}}{{\mathit{num}\left( {\mathit{tota}{\mathit{l}_ - }\mathit{edge}} \right)}}, $ | (5) |
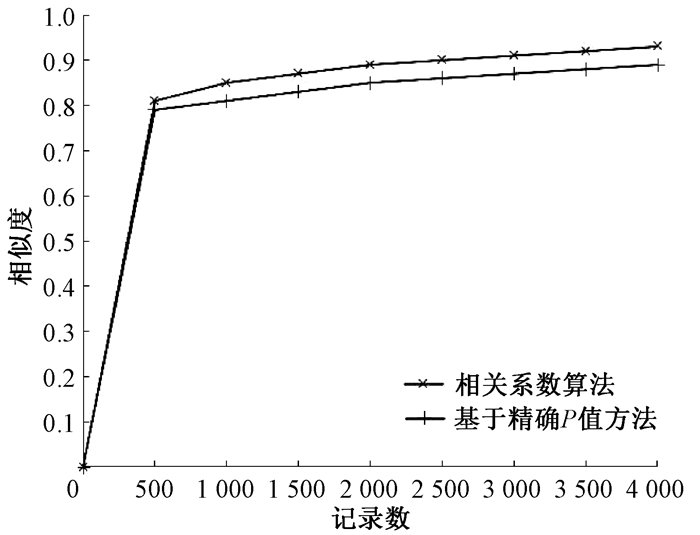
式中:分母表示两个CP-nets结构中边的总数; 分子表示两个CP-nets结构中具有相同起点、终点和相同方向的边的总数。基于精确P值方法学习CP-nets结构, 是根据Dijkstra原理对可行父亲集Pare(Xi)的对应值进行排序以获得CP-nets结构。将相关系数算法和基于精确P值方法分别在Netflix数据集和MovieLens数据集下进行相似度比较, 结果如图 1、图 2所示。可以看出, 在不同数据集中, 相关系数算法的相似度均高于精确P值方法, 这表明相关系数算法在CP-nets结构学习方面具有更好的效果。
|
图 1 Netflix数据集下不同算法的相似度 Fig. 1 The similarity of the different algorithms on the Netflix dataset |

|
图 2 MovieLens数据集下不同算法的相似度 Fig. 2 The similarity of the different algorithms on the MovieLens dataset |
加速比通常被用来评估一个算法并行化的效果, 可以很好地衡量节点数增加时算法效率提高的程度。设一台计算机完成一个串行算法所需要的时间为Ts, 多台计算机并行完成一个算法所需要的时间为Tp, 那么加速比为S=Ts/Tp。
为了衡量相关系数算法在不同规模数据集下的并行效果, 分别使用1个节点、2个节点和3个节点的Netflix和MovieLens数据集学习CP-nets结构, 记录不同节点数时算法的运行时间, 结果如表 1所示。可以看出, 在数据集大小保持不变的情况下, 随着节点数的增加, 算法的运行时间逐渐减少, 数据集的总体性能得到提高。此外, 随着数据集记录条数的增大, 算法的运行时间增加。
|
|
表 1 Netflix和MovieLens数据集下算法的运行时间 Tab. 1 Algorithm running time on the Netflix and MovieLens dataset |
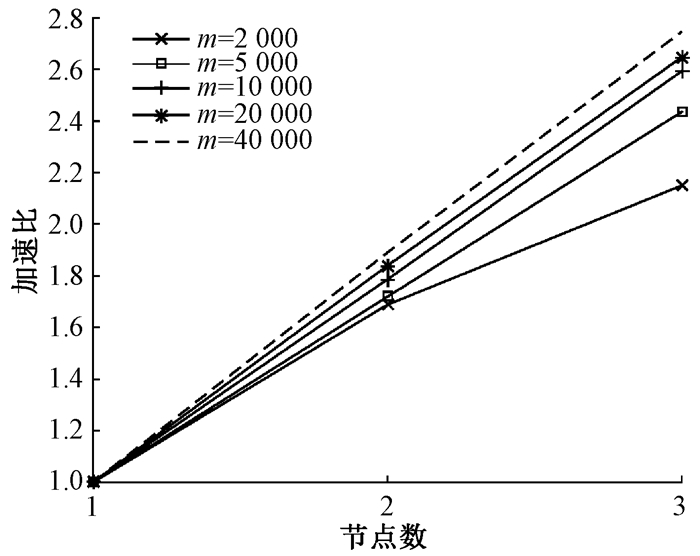
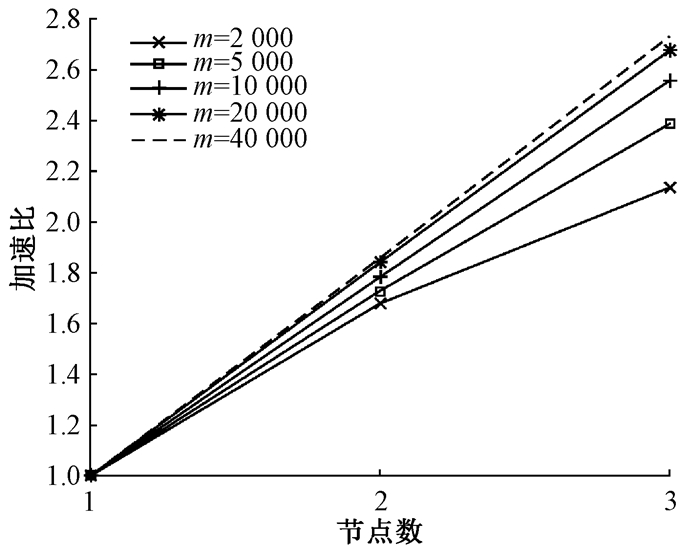
Netflix数据集和MovieLens数据集下算法的加速比结果如图 3、图 4所示。可以看出, 在数据集大小保持不变的情况下, 增大节点数, 算法总体性能随之增强; 当节点数恒定时, 随着数据集记录条数的增大, 加速比也增加。在数据集较小时, 加速比随着节点数的不同变化幅度较小。随着数据集的增大, 加速比曲线更接近于线性, 表明加速比不仅取决于节点数, 还取决于数据集的大小。
|
图 3 Netflix数据集下算法的加速比 Fig. 3 The speedup of the algorithm on the Netflix dataset |
|
图 4 MovieLens数据集下算法的加速比 Fig. 4 The speedup of the algorithm on the MovieLens dataset |
本文提出了一种从偏好数据库中基于MapReduce框架学习CP-nets结构的相关系数并行算法, 在两类电影推荐数据集下对算法进行了评估。实验结果表明, 该算法具有较高的准确性, 可以学习获得与原模型具有较高相似度的CP-nets结构, 与本文后续目标的性能接近。本文设计的算法具有较高的延展性, 为今后的研究工作奠定了基础。下一阶段的工作主要包括以下2个方面:运用特征选择中的方法, 考虑树形等特殊结构的CP-nets结构学习; 借鉴贝叶斯网络结构学习的方法, 继续探索其他更适合于在大规模数据集下进行CP-nets结构学习的方法。
| [1] |
BOUTILIER C, BRAFMAN R I, DOMSHLAK C, et al. CP-nets: a tool for representing and reasoning with conditional ceteris paribus preference statements[J]. Journal of artificial intelligence research, 2004, 21(1): 135-191. (  0) 0) |
| [2] |
ALANAZI E, MOUHOUB M. Variable ordering and constraint propagation for constrained CP-nets[J]. Applied intelligence, 2016, 44(2): 437-448. DOI:10.1007/s10489-015-0708-4 (  0) 0) |
| [3] |
范会涛, 冯涛. 基于聚类思想的加权条件熵及属性约简[J]. 郑州大学学报(理学版), 2018, 50(1): 39-46. FAN H T, FENG T. The weighted conditional entropy and attribute reduction based on clustering[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(1): 39-46. (  0) 0) |
| [4] |
GOUDIE R J B, MUKHERJEE S. A Gibbs sampler for learning DAGs[J]. Journal of machine learning research, 2016, 17(30): 1-39. (  0) 0) |
| [5] |
辛冠琳, 刘惊雷. 基于精确P值计算学习无环CP-nets[J]. 南京大学学报(自然科学), 2017, 53(3): 450-461. XIN G L, LIU J L. Learning acyclic CP-nets based on exact P-value computation[J]. Journal of Nanjing university (natural sciences), 2017, 53(3): 450-461. (  0) 0) |
| [6] |
LIU J T, YAO Z J, XIONG Y, et al. Learning conditional preference network from noisy samples using hypothesis testing[J]. Knowledge-based systems, 2013, 40(1): 7-16. (  0) 0) |
| [7] |
申金媛, 李航, 刘润杰, 等. 基于相关系数的有效特征光谱筛选方法[J]. 郑州大学学报(理学版), 2017, 49(3): 28-31. SHEN J Y, LI H, LIU R J, et al. Screening the effective spectrum features based on correlation coefficient[J]. Journal of Zhengzhou university (natural science edition), 2017, 49(3): 28-31. (  0) 0) |
| [8] |
GONZALES C, PERNY P, DUBUS J P. Decision making with multiple objectives using GAI networks[J]. Artificial intelligence, 2011, 175(7/8): 1153-1179. (  0) 0) |
| [9] |
YUAN C, MALONE B, WU X. Learning optimal Bayesian networks using A* search[C]//22nd International Joint Conference on Artificial Intelligence. Barcelona, 2011: 2186-2191.
(  0) 0) |
| [10] |
YUE K, FANG Q Y, WANG X L, et al. A parallel and incremental approach for data-intensive learning of Bayesian networks[J]. IEEE transactions on cybernetics, 2015, 45(12): 2890-2904. DOI:10.1109/TCYB.2015.2388791 (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


