2. 河北大学 数学与信息科学学院 河北 保定 071002
2. College of Mathematics and Information Science, Hebei University, Baoding 071002, China
19世纪初凸几何成为数学的一个独立分支[1-2]。伽罗瓦连接根基于伽罗瓦格理论[3],而伽罗瓦格理论是形式概念分析(formal concept analysis,FCA)[4]的核心,每一对伽罗瓦连接与伽罗瓦格之间存在一一对应。一些研究人员已将凸几何的方法应用于FCA研究中[5]。由于反拟阵与凸几何之间有一一对应关系[2],使得研究凸几何与伽罗瓦连接之间的关系,与研究反拟阵与伽罗瓦连接之间的关系具有一致性。寻找更为有效的方法来构造一个形式背景的伽罗瓦格,是FCA研究所面临的问题之一。研究反拟阵或凸几何与伽罗瓦连接的关系,是解决上述FCA问题的基础,也可将反拟阵和凸几何加入到FCA研究中以得到新的结果,这也是本文的主要研究目的。
虽然目前已经有较多的生物分类方法,但将信息提取方法融入生物分类学[6]研究中是亟须解决的问题之一。本文将探索解决该问题所需的基本理论,主要包括以下3项工作:(Ⅰ)对于一个凸几何(G, τ),是否存在一个伽罗瓦连接(K, L)满足LK=τ?若为是,这样的(K, L)在映射相等的观点下是否唯一?若不唯一,在何种思想下可以唯一?(Ⅱ)对于一个伽罗瓦连接(K, L),是否有一个凸几何(G, τ)满足τ=LK?若为否,则何时可为是?(Ⅲ)对一个伽罗瓦连接(K, L),给出一方法构造反拟阵,且利用此方法判定(G, LK)的凸几何性质。此外,本文利用上述方法对一个生物信息系统实例进行了分类。
1 一些定义和引理本节将给出后续工作所需的一些基本定义和性质,其他内容如格论可参考文献[7],FCA可参考文献[4]。本文所有考虑均为有限的,2A代表集合A的所有子集族。
定义1[2, 4] (1)若集合G上的一个函数τ: 2G→ 2G满足:对于任意的A,B⊆ G,有以下条件成立,① A⊆τ(A); ② A⊆B
(AE) 若闭包算子τ满足条件反交换性:对任意的X⊆G, y, z∈G且y≠z, 有y, z∉τ(X)且z∈τ(X∪y)
(2) 令F⊆2G,若F满足条件(a1):对于每个非空集合X∈F,一定存在一个x∈X满足X\x∈F;以及(a2):X, Y∈F
(3) 称格L为半模的,如果对于∀x, y∈L都有:若y覆盖x∧y,则必有x∨y覆盖x。
注1 闭包算子有多种定义方式,本文采用文献[2]中相关定义。
引理1[2] (1)令N为集合G满足如下性质的子集族:① G∈N;② X, Y∈N
(2) 设F⊆2G且N={G\X: X∈F},τ是由N产生的闭包算子,则(G, F)为反拟阵⇔(G, τ)为凸几何。
(3) 令F ⊆2G满足条件(a1),则(G, F)为反拟阵当且仅当(F, ⊆)为半模格。
注2 若集合系统(G, N)满足引理1(1)中的①和②,且相应的闭包算子满足(AE),则反拟阵和凸几何之间存在一一对应F
定义2[3] 令G和M为两个集合,Φ为G和M之间的二元关系,即Φ⊆G×M。对于G的任意子集X,令K(X)={y∈M:对于所有x∈X,有(x, y)∈Φ};对于M的任何子集Y,令L(Y)={x∈G:对于所有y∈Y,有(x, y)∈Φ}。则这一对映射(K, L)是G与M之间的一个伽罗瓦连接。
注3 (1)在文献[4]中称定义2中(G, M, Φ)为一个形式背景。对于(A, B)⊆(G, M),若A=L(B)且B=K(A),则称(A, B)为一概念,A为概念(A, B)的外延,B为概念(A, B)的内涵。全体概念关于概念之间的泛化和例化关系构成一个格,此格称为(G, M, Φ)的伽罗瓦格,记为Gal(G, M, Φ)。
(2) 由定义2知,伽罗瓦连接(K, L)是由形式背景(G, M, Φ)产生的,而形式背景(G, M, Φ)是由(K, L)产生的。
引理2[3] 令G和M为两个集合,(K, L)为G和M之间的伽罗瓦连接。那么映射LK是G上的一个闭包算子,KL是M上的一个闭包算子。
注4 文献[5]中定理5指出:对于一个伽罗瓦连接(f, g),若想讨论gf和fg的性质,则仅需考虑gf和fg中的一个即可。因此引理2对于工作(Ⅰ)和(Ⅱ)是有意义的。
说明1 (1)令(G, M, Φ)为一个形式背景,从文献[4]发现有一个形式背景(G1, M1, Φ1)满足L1K1(∅)=∅,其中G1=G\{g:对于任何的m∈M,有(g, m)∈Φ},M1=M\{m:对于任何的g∈G,有(g, m)∈Φ},并且对于任意的x∈G1和y∈M1,有(x, y)∈Φ1 ⇔ (x, y)∈Φ。此外(K1, L1)是由(G1, M1, Φ1)产生的。
(2) 由于Gal(G1, M1, Φ1)≌Gal(G, M, Φ),故对于(G, M, Φ)的讨论仅需研究(G1, M1, Φ1)[4]。
(3) 从文献[4]以及上述内容可知,即使有LK(∅)=∅的限制,也不会影响对伽罗瓦连接的讨论。同时,即使τ(∅)=∅,也不会影响对凸几何的研究,故本文所有结果对凸几何亦成立。
2 工作(Ⅰ)~(Ⅲ)本节将给出伽罗瓦连接和凸几何之间的关系,并且完成工作(Ⅰ)~(Ⅲ)。
首先,完成工作(Ⅰ)。
定理1 设(G,τ)为一个凸几何,
(1) 定义一个二元关系R⊆G×2G为(x, Y)∈R ⇔ Y=τ(Y)且x∈Y。令(K,L)是由(G, 2G, R)产生的伽罗瓦连接,则LK=τ成立。
(2) 定义R2⊆G×M为(x, Y)∈R2 ⇔ x∈Y, 且M={X⊆G: τ(X)=X}。令(K2, L2)是由(G, M, R2)产生的伽罗瓦连接,则L2K2=τ成立。
证明 先证明(1)。由R的定义以及注3(1)可保证(G, 2G, R)为一个形式背景。设X⊆G且N为τ的所有闭集构成的集族,从定义2导出K(X)={Y∈2G: ∀ x∈X,(x, Y)∈R}={Y∈N:∀ x∈X,x∈Y}。因此,对于∀Y∈K(X)和∀x∈X,必有(x, Y)∈R,也就是x∈Y。这就导出X⊆Y,根据定义1(1)中的①和②可得X⊆τ(X)⊆ τ(Y)=Y,故τ(X)∈K(X)。一方面,由定义2可知LK(X)={a∈G: ∀Y∈K(X), (a, Y)∈R}。运用τ(X)∈K(X)导出对任意的a∈LK(X),必有(a, τ(X))∈R,即a∈τ(X),故得LK(X)⊆τ(X)。另一方面,对任意的Y∈K(X),τ(X)⊆Y表明对任意的z∈τ(X),必有z∈Y成立,即(z,Y)∈R。进一步地,z∈LK(X)成立,亦即τ(X)⊆ LK(X)。总之有LK=τ成立。
再证明(2)。利用(1)的证明并结合R2的定义,则可得L2K2=τ成立。
定理1解决了对一个凸几何(G, τ),存在一个伽罗瓦连接(K, L)满足LK=τ的问题,同时发现(K, L)在通常映射相等的观点下不唯一。依据数学理论观点,同构意义下的数学结构视为同一个结构。因此,考虑在何种同构思想下,这样的(K, L)能够唯一。为此,给出定义3。
定义3 设(Oj, Pj, Rj)为一个形式背景,并且对应的伽罗瓦连接为(Kj, Lj)(j=1, 2)。若存在一个双射π:O1→O2满足条件:对于任意的X⊆O1,X=L1K1(X) ⇔ πX=L2K2(πX),则
(1) (K1, L1)是伽罗瓦同构于(K2, L2);
(2) 称π为一个(K1, L1)和(K2, L2)之间的伽罗瓦同构映射。
注5 将定义3与文献[4]中定义86进行比较得出:伽罗瓦同构是比两个形式背景之间的同构定义要弱的一种映射形式,即定义3在适用范围方面要比两个形式背景之间的同构更为广泛。
定理2 设(G, τ)为一个凸几何,则在伽罗瓦同构意义下,存在且仅存在唯一一个伽罗瓦连接(K, L)满足LK=τ。
证明 由定理1和定义3可得定理2。
说明2 对于凸几何(G, τ), 定理1以构造方式发现一个伽罗瓦连接(K, L)使其满足LK=τ。定理2保证了在伽罗瓦同构意义下(K, L)的唯一性。
其次,完成工作(Ⅱ)。
令(K, L)为集合G和M之间的一个伽罗瓦连接,以及有G上的一个伽罗瓦连接τ,是否有LK=τ?例1给出一个否定的回答。
例1 设k为一个正整数并且I={X⊆G: X≤ k},由文献[8]第10页知(G, I)为拟阵。根据文献[8]第8页定理4知:(G, I)的闭包算子σ满足定义1(1)的条件,并且当|X|≤k-1时,有σ(X)=X;当|X|≥k时,有σ(X)=G。
设X⊆G且|X|=k-1, 选取 y, z∈G\X且y≠z, 则有σ(X)=X, 以及X∪y,X∪z⊆G和|X∪y|=|X∪z|=k。因此σ(X∪y)=σ(X∪z)=G,从而z∈G=σ(X∪y)和y∈σ(X∪z)。故σ不满足条件(AE),即(G, σ)不是凸几何。定义R⊆G×2G为(x,Y)∈R⇔ Y=σ(Y)且x∈Y,可以证明,由(G, 2G, R)产生的伽罗瓦连接(K, L)满足LK=σ。对任意凸几何(G, τ),因τ不一定为σ,故不一定有LK=τ。
下面给出LK=σ成立的证明。
从LK⊆σ和σ⊆LK两个方面加以证明。令X⊆G,一方面,因为K(X)={Y∈2G: ∀x∈X,(x,Y)∈R}={Y: ∀x∈X,x∈Y=σ(Y)},可导出X⊆Y=σ(Y),故X⊆σ(X)⊆σ(Y)=σ(σ(Y))=Y成立,因此σ(X)∈K(X)。由于LK(X)={a∈G: ∀Y∈K(X),(a,Y)∈R},并且结合σ(X)∈ K(X)导出,对于任意的a∈LK(X)必有(a,σ(X))∈R,即a∈σ(X), 从而LK(X)⊆σ(X)成立。另一方面,对任意的Y∈K(X),σ(X)⊆Y表明对于任意的b∈σ(X),必有b∈Y成立,即(b, Y)∈R。因此,b∈LK(X)是正确的, 从而σ(X)⊆LK(X)成立。
定理3将给出在什么条件下,一个伽罗瓦连接(K, L)和凸几何(G, τ)满足LK=τ。
定理3 令(K, L)为G和M之间的一个伽罗瓦连接,
(1) LK满足条件(AE)当且仅当存在一个凸几何(G, τ)满足LK=τ。
(2) 设F={G\Y: Y=LK(Y)}, F满足定义1(2)中的(a1),并且(F, ⊆)是一个半模格当且仅当(G, LK)是一个凸几何。
证明 由引理2和定义1易得(1)。由引理1易证明(2)。
再者,完成工作(Ⅲ)。
定理3可以发现在什么条件下一个伽罗瓦连接(K, L)对应一个凸几何,但可惜不是用构造性方法。下文将用构造性方法确定(G, LK)的凸几何性质。由引理1及注2知:(G, LK)的凸几何性质是由(G, {Y⊆G: Y=LK(Y)})在反拟阵方面的性质所决定的。故给出判定一个伽罗瓦连接产生凸几何性质的方法,其思路如下:令(K, L)为集合G和M之间的一个伽罗瓦连接,以及F={G\Y: Y=LK(Y)}。设(G, M, R)为由(K, L)产生的形式背景,从文献[4]可得如下陈述:
(1) 在伽罗瓦连接集合与形式背景集合之间存在一一对应关系; 在形式背景集合与伽罗瓦格集合之间存在一一映射。
(2) 设B(G)={A⊆G:存在B⊆M使得(A, B)∈Gal(G, M, R)},则格(B(G), ⊆)同构于Gal(G, M, R)。
(3) 设B(LK)={Y: Y=LK(Y)},则B(G)=B(LK)。
(4) 有许多构造B(G)或(B(G), ⊆)的方法。
陈述(1)~(4)意味着F={G\Y: Y∈B(LK)}可选任意构造B(G)的方法[4],用于寻找出F,进一步地,找到(F, ⊆)。同时,在FCA中一些构造B(G)的算法可以用于构造(B(G), ⊆)的Hasse图。如果使用这些算法,由于(F, ⊆)是(B(G), ⊆)的对偶,则可以构造出(F, ⊆)的Hasse图。从(F, ⊆)的Hasse图中可以很容易地确定(F, ⊆)的半模性,进而可以判定(F, ⊆)是否为一个反拟阵。文献[9]给出一些判定一个结构为反拟阵的算法,也可以用这些算法判定(F, ⊆)的反拟阵性质。同时,(G, LK)的凸几何性质也可以利用引理1加以判断。
3 应用举例本节用一个实例说明上述一些结论的具体应用。
例2 给定原始生物信息系统(O1, P1, R1),其中O1={纺织娘1,纺织娘2,纺织娘3}, P1={体长,翅长,翅宽,前胸背板长,前胸背板高}, 生物信息背景R1如表 1所示。根据文献[10]的操作过程,可以将表 1转化为如表 2所示的二元化生物信息背景。表 2中的1表示该行的生物个体拥有对应该列的生物特征,0表示该行的生物个体不拥有对应该列的生物特征。
|
|
表 1 生物信息背景 Tab. 1 Biological information context |
|
|
表 2 二元化生物信息背景 Tab. 2 Binary biological information context |
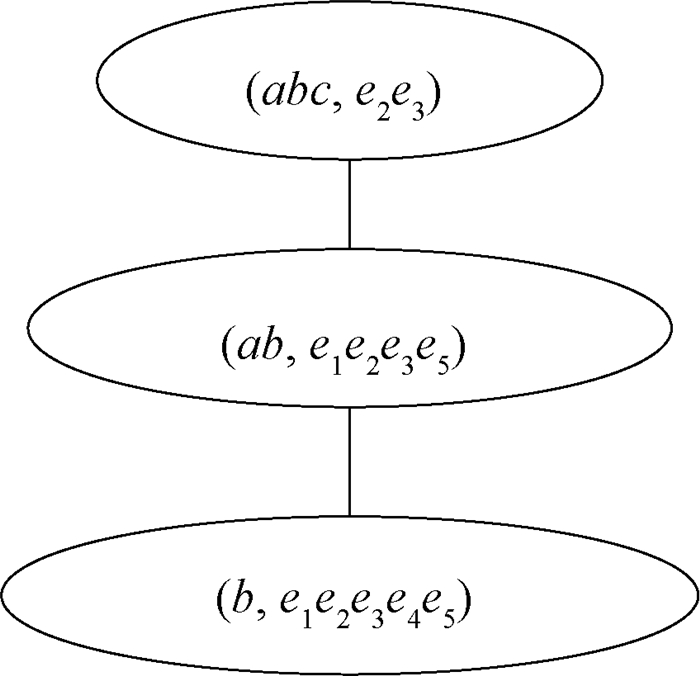
若令纺织娘1为a, 纺织娘2为b, 纺织娘3为c, 体长为e1,翅长为e2,翅宽为e3,前胸背板长为e4,前胸背板高为e5, 则可以得到与表 2对应的形式背景(O2, P2, R2)的数学表示,如表 3所示。利用文献[4]中的方法,可以生成与表 3对应的伽罗瓦格,如图 1所示。为简洁起见,将{X}简记为X,其中{X}⊆O2或者{X}⊆P2。
|
|
表 3 二元化生物信息背景的数学表示 Tab. 3 Mathematical representation of binary biological information context |
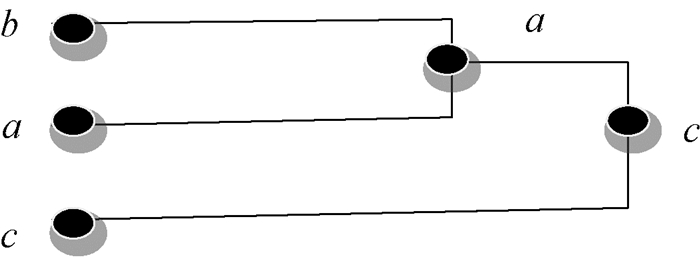
如果令F={{b}, {a, b}, {a, b, c}}, 利用定义1 (3)易知(F, ⊆)是一个半模格,再利用引理1知(O2, F)为一个反拟阵。事实上,依据表 1~3的关系以及生物形态学知识可知,(b, e1e2e3e4e5)表示纺织娘2拥有5个生物特征e1、e2、e3、e4、e5;(ab, e1e2e3e5)中的ab在(F, ⊆)中满足{a, b}覆盖{b},该特点表明{a, b}\{b}中的元,即纺织娘1具有纺织娘2的祖先特征,这几个特征是e1、e2、e3和e5。在(F, ⊆)中{a, b, c}覆盖{a, b}表明{a, b, c}\{a, b}中的元,即纺织娘3具有纺织娘1和纺织娘2的祖先特征,这些特征是e2和e3。原始生物信息背景的生物特征分析树状结构如图 2所示。此处,N={{a, b, c}\X: X∈F}={{a, c}, {c}, ∅},产生的闭包算子τ为τ(A)=∩{Y: A⊆Y且Y∈N},满足τ(∅)=τ({a, b})=τ({b, c})=τ({b})=τ({a, b, c})=∅, τ({a})=τ({a, c})={a, c}, τ({c})={c}。由上面讨论和引理1(2)可以得到({a, b, c}, τ)是一个凸几何。
|
图 2 原始生物信息背景的生物特征分析树状结构 Fig. 2 Tree structure of biological characteristic analysis for raw biological information context |
设X⊆{a, b, c}和Y⊆{ej: j=1, …, 5},令K(X)={y∈{ej: j=1, …, 5}:对于X中任意的x满足与y在表 3中对应值为0}, L(Y)={x∈{a, b, c}:对于Y中任意的y满足与x在表 3中对应值为0}。则LK(∅)=LK({a, b})=LK({b, c})=LK({b})=LK({a, b, c})=∅,LK({a})=LK({a, c})={a, c},LK({c})={c}。(K, L)就是(O2, P2, R2C)产生的伽罗瓦连接,显然有LK=τ,此处R2C={(x, y): (x, y)∈O2×P2, 且(x, y)∈R2不成立}。
注6 例2表明,在一个生物信息系统组成的形式背景(G, M, Φ)中,G是生物个体集合,M是生物特征集合,Φ⊆G×M。若令F⊆2G, 在(F, ⊆)中,对于任意的x, y∈F, 当x覆盖x∧y, 则表明生物集合x\x∧y中的生物个体拥有生物群体x∧y的祖先特征。如果(F, ⊆)为一个半模格,那么x∨y\y中的生物个体都拥有生物群体y的祖先特征。这一推测对于生物的系统发育问题会有所帮助,也显示出考虑半模格的优势所在。
即使(F, ⊆)不为半模格,也可以借用半模格的性质进行讨论。对于任意的x, y∈F, 下文将根据x, y之间的关系,分成状态1~3研究拥有x与y的祖先特征问题。
状态1 设x, y在(F, ⊆)中可比较,不妨设在(F, ⊆)中x < y, 并且xi+1覆盖xi(i=0, 1, …, n-1),x0=x, xn=y, 则借用例2中的方法,经过n步可以得到y\xn-1中的元所具有的x的祖先特征,此外还可以得到生物特征分析树状结构。
状态2 设x, y在(F, ⊆)中不可比较,分以下3种情况进行讨论。
情况1 在(F, ⊆)中x, y无公共上界。
该情况表明在(F, ⊆)中x, y无共同的祖先特征。
情况2 在(F, ⊆)中x, y有唯一的公共上界x∨y。
① 设从y到x∨y的极大链为{y, yi1, …, yi(mi-1), x∨y}(i=1, 2, …, ny)。
② 利用状态1可以得到x∨y\yi(mi-1)以及该集合中的生物个体集合拥有的公共生物特征Yiy, 这也就是x∨y\yi(mi-1)拥有的yi(mi-1)(i=1, 2, …, ny)的祖先特征。
③ 对x, 令x=y,重复①和②,得到x∨y\xi(si-1)以及该集合中的生物个体集合拥有的公共生物特征Xix, 这也就是x∨y\xi(si-1)拥有的xi(si-1)(i=1, 2, …, nx)的祖先特征。
④ 令A=x∨y\((y1(m1-1)∪…∪yny(mny-1))∩(x1(s1-1)∪…∪xnx(snx-1))),B=((Y1y∩…∩Ynyy)∩(X1x∩…∩Xnxx))。则A中的元具有(y1(m1-1)∪…∪yny(mny-1))∩(x1(s1-1)∪…∪xnx(snx-1))的公共祖先特征就是B。再由y∩x⊆ (y1(m1-1)∪…∪yny(mny-1))∩(x1(s1-1)∪…∪xnx(snx-1)), 说明A中的元拥有x和y的祖先特征。
情况3 在(F, ⊆)中x, y有不唯一的公共上界(xy)1, …, (xy)t (t>1)。
对于每一个(xy)i, 重复情况2,可以得到相应的Ai和Bi (i=1, 2,…, t)。利用凸几何的闭包算子和伽罗瓦连接的产生过程,这时如果在(F, ⊆)中存在包含有A1∪…∪At的最小元C,则C中的元拥有x和y的祖先特征B1∩…∩Bt。如果这样的C不存在,则也说明Ai拥有x和y的祖先特征。
对上述情况分析如下:①对于情况2和情况3中存在C,这时关于x和y与x∨y或C产生的生物特征分析的树状结构图是有根树;对于情况3中不存在C,这时关于x和y以及(xy)1, …, (xy)t产生的生物特征分析的树状结构图是无根树。对于情况1,此时与x和y有关的生物特征分析的树状结构图是无根树。②三种情况的讨论完全是依据偏序集理论和格论,以及伽罗瓦连接的思想进行的,并无任何其他推测,所以可以保证结果在数学理论方面的正确性。由于遍历了所有可能的结果,因此从生物分类角度而言也是可行和可信的。
状态3 设x, y在(F, ⊆)中不可比较,对于状态2的情况1,由于结论简单,这里不再讨论。对于状态2的其他两种情况,给出一种不同于状态2的求法,分以下两部分进行讨论。
第1部分:对于状态2中的情况2,分两种子情况加以讨论。
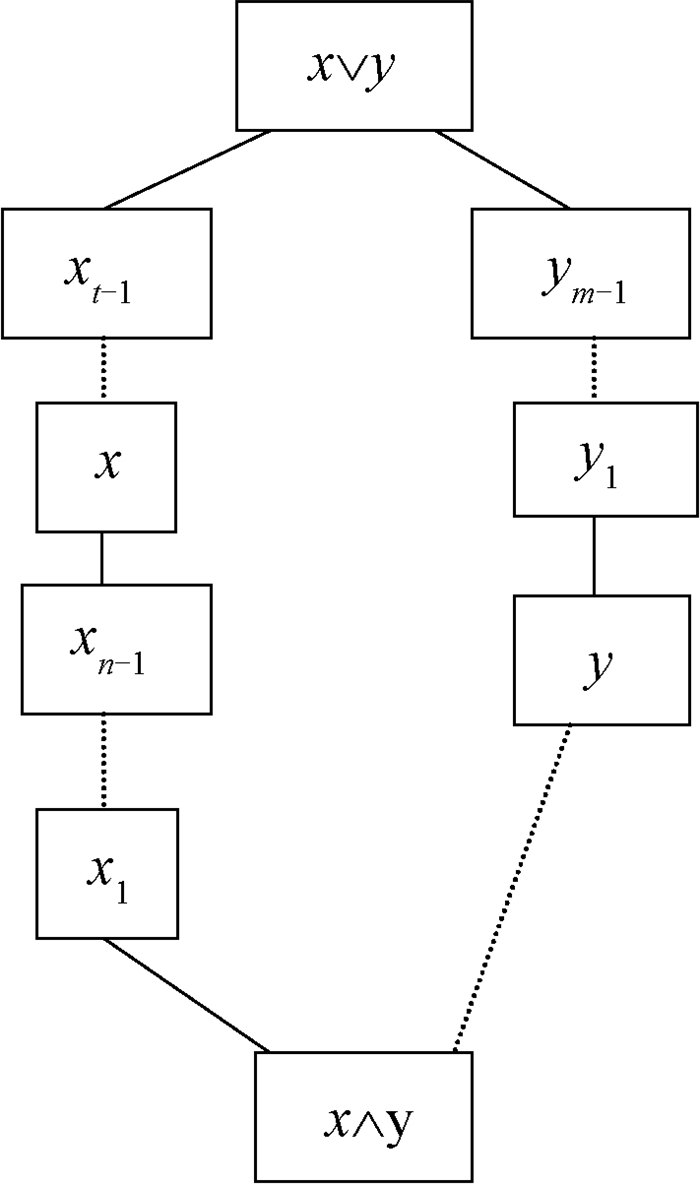
子情况1 (F,⊆)中两个元x, y的关系见图 3,其中的实线表示覆盖关系,虚线表示两个元之间有链关系。求取x∨y与x和y的祖先特征关系的思路如下。
|
图 3 (F, ⊆)中两个元x, y的关系 Fig. 3 Relationship between two elements x and y in (F, ⊆) |
第1步 将x1视为一个外群个体集合,将x1与yj(j=1, …, m-1, m)之间分别做假设的连线,此处做实线,并且x∨y=ym。
第2步 ({x∧y, x1, y, y1}, ⊆)构成一个半模格,利用半模性推测出y1\(x1∪y)具有的x1和y的哪些祖先特征,事实上,若用z′表示生物个体z的生物特征集合,则这些特征是x′1∩y′, 将所得y1与x1和y的那些祖先特征与y′1求交集,替换掉y1原先具有的生物特征。
第3步 令y=y1, y1=y2, 重复第1、2步。由于采用的生物样本的有限性,导致了所考虑的生物个体集合的有限性。也就是经过m次重复, 一定可以推测出x∨y\\ym-1具有的x1和ym-1的可能祖先特征。
第4步 令x1=x2, 重复第1~3步,由于x∨y的有限性,可知x1, …, xn-1的有限性,如此经过n次重复,可以得到x∨y\ym-1具有的x和ym-1的可能祖先特征。
第5步 由于考虑{x∧y, xi, yj, y}的可能祖先特征关系时,得到的是yj\y具有xi(i=1, …, n-1, n; j=1, …, m-1, m)和y的可能的祖先特征,其中x=xn,x∨y=ym。将所有这些祖先特征集合求交集,推测出x∨y\(x∪y)具有的x和y的一些祖先特征,此处是利用伽罗瓦连接与凸几何运算的定义推测的。
对子情况1分析如下:①在第1步中做假设的连线是可行的,因为在系统发育分析时,有时是允许假设一个外群,例如做系统发育分析时常用的Hennig方法[11]。②从对应的思路过程可以看出,x∧y在求得最后结果的过程中几乎没有作用。如果x∧y不存在时,可以假设一个下界,不妨设∅∈F,这是由于∅′=M,所以在上述过程中,所有结果均不受影响。
子情况2 若x和y之间有唯一上界x∨y,但是从y到x∨y,以及从x到x∨y的极大链不一定是唯一的,则对于每对从y到x∨y的极大链和从∅到x的极大链,重复子情况1,类似状态2中情况2的④,可以得到所需的祖先特征关系。
第2部分:对于状态2中的情况3进行讨论。
对于每个x和y的上界,重复第1部分,其他类似状态2中情况3的讨论。
需要说明的是:①状态2和状态3只是理论上的方法和想法,还需具体的算法实现以及生物分类实践的检验,并与已有方法进行比对,这些研究将在后续工作中进行。②虽然Gal(G, M, Φ)的外延全体(GalG(G, M, Φ), ⊆)不一定是半模的,但是在某些情况下,比如例2的情况,或者只考虑(GalG(G, M, Φ), ⊆)部分时,有可能是半模的,这样利用反拟阵的性质[2]可以很快地解决所要讨论的问题。另外,如果需要考虑N={G\X: x∈GalG(G, M, Φ)}的情况,则可以利用凸几何的性质[1]迅速地发现所需答案。再有,上面的讨论是GalG(G, M, Φ),事实上,由伽罗瓦连接与反拟阵和凸几何的关系可知,不一定用(G, M, Φ)的伽罗瓦格,可更为一般化地用伽罗瓦连接讨论一个生物信息组成的形式背景中生物个体集合之间的关系。
4 结束语本文借助反拟阵讨论凸几何与伽罗瓦连接之间的关系,利用凸几何与反拟阵之间的对应关系,以及FCA中伽罗瓦连接与伽罗瓦格的联系、伽罗瓦格与反拟阵的半模性的联系,得到判定一个伽罗瓦连接产生的几何是否为凸几何的方法,该方法为用反拟阵和凸几何方法研究FCA提供了思路。未来将尝试进一步地发展和实现这些想法和思路。
| [1] |
COPPEL W A. Foundations of convex geometry[M]. Cambridge: Cambridge University Press, 1998.
(  0) 0) |
| [2] |
BJÖRNER A, ZIEGLER G M. Introduction to greedoids[M]//Matroid Applications. Cambridge: Cambridge University Press, 1992: 284-357.
(  0) 0) |
| [3] |
STEWART I. Galois theory[M]. 2nd ed. New York: Champman and Hall Ltd., 2011.
(  0) 0) |
| [4] |
GANTER B, WILLE R. Order-theoretic foundations[M]//Formal Concept Analysis. Berlin: Springer, 1999: 1-15.
(  0) 0) |
| [5] |
MONJARDET B. Some order dualities in logic, games and choices[J]. International game theory review, 2007, 9(1): 1-12. (  0) 0) |
| [6] |
蔡邦华. 昆虫分类学[M]. 北京: 化学工业出版社, 2017. CAI B H. Insect taxonomy[M]. Beijing: Chemical Industry Press, 2017. (  0) 0) |
| [7] |
GRÄTZER G. Lattice constructions[M]//Lattice Theory: Foundation. Basel: Springer, 2011: 255-306.
(  0) 0) |
| [8] |
WELSH D J A. Matroid theory[M]. London: Academic Press, 1976.
(  0) 0) |
| [9] |
KEMPNER Y, LEVIT V E. Correspondence between two antimatroid algorithmic characterizations[J]. The electronic journal of combinatorics, 2003, 10(1): 1-12. (  0) 0) |
| [10] |
毛华, 杨兰珍, 蔺庚梅, 等. 渐进式生物聚类信息提取软件V1.0: 2017SR129228[P]. 2017-02-20. MAO H, YANG L Z, LIN G M, et al. A software for information extraction of gradual biological clustering V1.0: 2017SR129228[P]. 2017-02-20. (  0) 0) |
| [11] |
梁爱萍. 介绍系统发育分析计算机程序HENNIG86(1.5版)[J]. 动物分类学报, 1993, 18(4): 499-502. LIANG A P. On the phylogenetic program HENNIG86(version 1.5)[J]. Acta zootaxonomica sinica, 1993, 18(4): 499-502. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53