0 引言

随着互联网数据的快速增长和网络应用的日趋丰富，用户需求逐渐从主机之间的通信演进为主机对网络信息的重复访问^[1-2].与传统网络架构中以IP地址进行路由的方式不同，信息中心网络(information-centric networking，ICN)^[3-4]通过唯一的内容名称对用户请求进行路由，且每个节点除了具有处理、转发的功能之外，还具有存储的功能^[5].网内缓存作为ICN最大特点之一^[6-7]，在提高用户服务质量、减少用户访问时延、减轻服务器负载上功不可没^[8].ICN缓存领域中很多关键技术已有了阶段性的创新，但仍值得深入分析和研究^[3].

在ICN众多研究项目中，最具代表性且最有发展前景的范例当属命名数据网络(named data networking，NDN)项目^[9-10].文献[11]为了充分利用ICN的内置缓存，提出了一种基于内容空间分区和哈希路由的缓存机制，将内容缓存在指定的划分区域中，能够解决哈希路由引起的路径拉伸问题.文献[12]提出了一种新型智能资源管理系统，旨在分析请求模式，充分利用通用缓存内容.该系统能够根据用户需求变化实时高效地进行缓存资源分配.文献[13]通过在转发信息库中添加路由缓存，包括原子缓存和即时缓存，来缓解转发信息库的爆炸问题.目前国内外学者在ICN体系结构、路由算法、缓存决策等方面已经取得了一定的成果，但是却鲜有针对缓存容量分配机制的研究.

ICN缓存容量分配面临着巨大的缓存对象与有限的缓存空间之间的矛盾^[14].绝大多数的ICN中都默认均匀部署路由器(即缓存容量相同).考虑到节点位置、网内流量分布以及用户请求特征不同，从根本上导致了节点负载不均衡.因此，如何将有限的总缓存容量适当地部署到更关键的位置，以平衡节点负载并提高缓存利用率尤为关键.

针对上述问题，本文在互联网主干网络的ICN网络架构下，分别从用户角度和节点角度对全局流量分布进行分析.首先分析网络拓扑属性以及流量特征信息，然后基于分析结果对网络节点进行聚类划分，并重新分配节点容量，旨在将有限的总缓存容量以最优的方式合理地分配给各节点，从而实现网络的负载均衡.

1 网络数据模型 1.1 拓扑信息

网络拓扑中的节点位置从根本上影响着该节点处理兴趣请求的概率，即位于网络中相对“枢纽”位置的节点可能需要处理更多的请求.因此，基于图论基础，选取了节点度数中心性C_d、节点介数中心性C_b、节点紧密中心性C_c 3个中心性指标作为网络拓扑属性来区分节点的重要程度.

节点度数中心性C_d的计算为${C_ - }{d_i} = \sum\limits_{k = 1}^n a \left( {{v_i}, {v_k}} \right)$, 其中：n是节点总数；a(v_i, v_k)是连接函数，如果节点v_i、v_k直接相连，那么a(v_i, v_k)值为1，否则为0；C_d表示与该节点直接相连的边数，用来分析节点的直接影响力.节点介数中心性C_b的计算为${C_ - }{b_i} = \sum\limits_{s \ne v \ne t \in V} {\frac{{{\sigma _{st}}(i)}}{{{\sigma _{st}}}}} $，其中：σ_st是点v_s到点v_t的所有最短路径数；σ_st(i)是其中经过节点i的路径数，节点介数中心性表示网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例，反映了该节点是否为“交通枢纽”，即在整个网络中的作用和影响力.节点紧密中心性C_c的计算为${C_ - }{c_i} = \frac{1}{{\sum\limits_{k = 1}^n d \left( {{v_i}, {v_k}} \right)}}$，其中：d(v_i, v_k)是节点v_i到节点v_k的最短路径长度.一个节点如果到其他所有节点的最短路径和越小，则该点就越靠近网络的中心位置，用来分析节点的相对位置.

1.2 流量特征信息

流量特征信息能够很好地反映网络流量的分布情况，为区分节点的重要程度，本文从节点负载和用户偏好两方面共选取5个指标作为流量特征信息属性.在节点负载方面，选取接收兴趣包个数Rec_I、响应请求次数Res_I以及内容替换次数Rep_C 3个指标.在用户偏好方面，选取兴趣聚合率Aggr和兴趣影响度Impact两个指标.其中，节点负载方面的3个指标可以通过采样单位时间段内的测量值累加统计得出.下面给出本文对兴趣聚合率和兴趣影响度的定义.

兴趣聚合率Aggr为节点v_i添加的接口数Nface_i与节点接收到的兴趣包数Rec_I_i的比值，如$Agg{r_i} = \frac{{Nfac{e_i}}}{{Re{c_ - }{I_i}}}$.兴趣影响度$\mathit{Im}pac{t_i} = \sum\limits_{j = 0}^{TTL} {\left( {Iho{p_j} \cdot \frac{1}{{j + 1}}} \right)} $.TTL为用户所能容忍的最大跳数.本文定义节点v_i响应的兴趣请求中，兴趣包经过跳数j的倒数和对应的兴趣包个数Ihop_j之积的总和为兴趣影响度.

1.3 信息整合模型

本文将提出的3个拓扑参数和5个流量信息参数作为评价节点重要程度的指标.使用x_i(t)表示，在单位取样时间段T内，节点v_i收集到的流量特征信息的数据，如公式(1)，

$ {x_i}(T) = \left\{ {\mathit{Re}{\mathit{c}_ - }{I_i}(T), \mathit{Re}{\mathit{s}_ - }{I_i}(T), \mathit{Re}{\mathit{p}_ - }{C_i}(T), \mathit{Agg}{\mathit{r}_i}(T), \mathit{Impac}{\mathit{t}_i}(T)} \right\}, $

(1)

其中：x_i(T)是五维数据，简写为x_i.单独收集一个时间段内的流量信息不能全面反映网内流量的变化情况，因此，总共需要选取T′个采样时间段进行流量信息的收集.用X_i表示在T′个采样时间段内节点v_i收集到的数据集为

$ {X_i} = \left\{ {{x_i}\left( {{T_1}} \right), {x_i}\left( {{T_2}} \right), \cdots , {x_i}\left( {T_T^\prime } \right), {C_ - }{d_i}, {C_ - }{b_i}, {C_ - }{c_i}} \right\}, i \in [0, n). $

(2)

结合公式(1)，可将公式(2)中的X_i展开

$ {X_i} = \left\{ {\mathit{Re}{\mathit{c}_ - }{I_i}\left( {{T_1}} \right), \mathit{Re}{\mathit{s}_ - }{I_i}\left( {{T_1}} \right), \mathit{Re}{\mathit{p}_ - }{C_i}\left( {{T_1}} \right), \mathit{Agg}{\mathit{r}_i}\left( {{T_1}} \right), \mathit{Impac}{\mathit{t}_i}\left( {{T_1}} \right), \cdots , \mathit{Re}{\mathit{c}_ - }{I_i}\left( {T_T^\prime } \right), \mathit{Re}{\mathit{s}_ - }{I_i}\left( {T_\tau ^\prime } \right)} \right., $

$ \mathit{Re}{\mathit{p}_ - }{C_i}\left( {T_T^\prime } \right), \mathit{Agg}{\mathit{r}_i}\left( {T_T^\prime } \right), \mathit{Impac}{\mathit{t}_i}\left( {T_T^\prime } \right), {C_ - }{d_i}, {C_ - }{b_i}, {C_ - }{c_i}\} , $

其中：X_i是(5T′+3)维的数据.考虑到拓扑中共有n个节点，因此，本文收集的数据集为n个(5T′+3)维的数据.

2 缓存容量分配机制 2.1 基于改进t-SNE算法的数据集处理

本文所收集的数据呈现高维特征，且对于每个节点而言高维数据之间存在数据冗余、信息重叠的问题.本文将使用改进的t-SNE算法^[15]对原数据进行降维，并通过VP树(vantage point tree)^[16]构建K-近邻.在高维空间中，已知x_i和x_j为任意的两个数据点，x_k为非x_i的数据点，Nei_i为x_i邻居集合，可通过对称化两个条件概率分布得到点对相似性的联合概率分布p_ij.而在本文收集的高维数据点中，两个相距较远的数据点的相似性概率p_ij非常小，因此取条件概率作为p_ij的近似.基于此，高维空间中数据点的点对相似性可定义为

$ {p_{j|i}} = \left\{ \begin{array}{l} \frac{{\exp \left( { - {{\left\| {{x_i} - {x_j}} \right\|}^2}/2\sigma _i^2} \right)}}{{\sum\limits_{k \in Ne{i_i}} {\exp } \left( { - {{\left\| {{x_i} - {x_k}} \right\|}^2}/2\sigma _i^2} \right)}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 如果\;j \ne i\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right.. $

(3)

高维数据是基于流形的^[17]，在高维空间中如果直接使用欧式距离会存在误差，因此本文将以测地线距离代替欧式距离.但是，高维数据中的真实测地线距离难以获得.考虑到每个输入对象x_i已有最近邻居集合Nei_i，本文将邻域内两个数据点间的最短路径计算值作为真实测地线距离的近似.x_i邻域Nei_i内任意两个数据点间的欧式距离记为d_X(x_i, x_j)，测地线距离记为d_G(x_i, x_j)，两者关系如公式(4)，然后计算x_i邻域Nei_i内任意两个数据点间的最短路径，如公式(5)，

$ {d_G}\left( {{x_i}, {x_j}} \right) = \left\{ \begin{array}{l} {d_X}\left( {{x_i}, {x_j}} \right), \;\;\;\;如果i、j相连\\ \infty , \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right.. $

(4)

$ {d_G}\left( {{x_i}, {x_j}} \right) = \min \left\{ {{d_G}\left( {{x_i}, {x_j}} \right), {d_G}\left( {{x_i}, {x_k}} \right) + {d_G}\left( {{x_k}, {x_j}} \right)} \right\}, \;\;\, k \in [0, n). $

(5)

基于此，公式(3)可改进为

$ {p_{j|i}} = \left\{ \begin{array}{l} \frac{{\exp \left( { - {{\left( {{x_i}, {x_j}} \right)}^2}/2\sigma _i^2} \right)}}{{\sum\limits_{k \in Ne{i_i}} {\exp } \left( { - {d_G}{{\left( {{x_i}, {x_k}} \right)}^2}/2\sigma _i^2} \right)}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 如果j \ne i\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right.. $

(6)

然后使用KL散度(Kullback-Leibler divergence)来衡量联合概率分布p_ij和q_ij之间的相似性.t-SNE最终目标就是对高维空间中所有数据点最小化代价函数C，$C = KL(P \parallel Q) = \sum\limits_i {\sum\limits_j {{p_{ij}}} } \log \frac{{{p_{ij}}}}{{{q_{ij}}}}$.在初始化的过程中，方差σ可以选择较小的值，使用随机梯度下降算法进行训练.在训练过程中，为了保证优化速度，同时防止陷入局部最优，需要引入3个参数，分别为迭代次数I、学习速率η和第i次迭代的动量参数α(i).在更新过程中，不仅需要考虑当前的梯度，还需要考虑之前迭代过程中梯度的指数衰减.根据文献[16]推导，迭代i次后的解 ${Y^{(i)}} = {Y^{(i - 1)}} + \eta \frac{{\delta C}}{{\delta Y}} + \alpha (i)\left( {{Y^{(i - 1)}} - {Y^{(i - 2)}}} \right)$.经过I次迭代后，得到低维嵌入的最终解Y^(I).

2.2 缓存容量分配

在通过构造K-近邻表征相似性的方式改进了t-SNE算法后，对收集到的高维数据进行处理，得到低维空间的嵌入结果Y^(I).本文以该降维结果作为节点相似性的划分标准，根据节点重要程度不同，设置不同的权重，进而按权重为节点分配不同大小的容量空间.

假设低维嵌入结果Y^(I)将节点划分为k_class类，num_j表示类别j中包含的节点个数.令W表示类别对应的权重值，W={w₁, w₂, …, w_k}，W中的变量按降序排列且满足公式(7)的约束，

$ \sum\limits_{j = 1}^k {{w_j}} = 1, 0 < {w_1} < \cdots < {w_k} < 1. $

(7)

假设整个网络拓扑的总缓存容量用C_total表示，在类别j中，节点的分配缓存大小用C_ji表示，

$ {C_{ji}} = {C_{{\rm{ total }}}} \cdot {w_j}/nu{m_j}, j \in [1, k], i \in \left[ {1, nu{m_j}} \right). $

(8)

缓存容量分配机制中，首先初始化参数并构建VP树；然后根据VP树构建K-近邻并计算点对之间的测地线距离；再计算高维空间联合概率分布；最后使用梯度下降法进行训练，得到低维嵌入的结果.通过构造K-近邻表征相似性的方式改进t-SNE算法，既考虑了高维数据的流形特征，也大大降低了高维空间点对相似性的计算量.

3 性能评价 3.1 拓扑用例

在进行仿真实现的过程中，本文使用了中国的cernet和美国的deltacom两种拓扑结构.cernet网络拓扑结构含有36个节点、49条链路，平均节点度数为2.72.deltacom网络拓扑结构含有113个节点、161条链路，平均节点度数为2.85.

3.2 评价指标

本文在Ubuntu下搭建基于NS-3的仿真模块NDNSIM并进行仿真实现，同时将搜集的历史流量数据导入到matlab软件中进行处理.

本文基于两种拓扑结构、采用多个性能指标对基于t-SNE算法的缓存容量分配机制进行性能评价，评价指标如下.

1) 缓存命中率.缓存命中率的计算公式CacheHitRatio=Num_cacheHit/Num_success，其中：Num_cacheHit为从路由器节点的内容存储库(content store, CS)获得内容的兴趣请求数；Num_success为路由成功的兴趣请求数.缓存命中率能够在很大程度上表征缓存内容的利用率.

2) 路由成功率.路由成功率的计算公式SuccessRatio=Num_success/Num_total，其中：Num_success为路由成功的兴趣请求数；Num_total为用户向网络中发起的兴趣请求总数.路由成功率能够表征路由机制的效率.

3) 缓存开销.节点缓存开销的计算公式Over_i=Rep_C_i·Vol_aver/c_i，其中：Rep_C_i为节点内容替换次数；Vol_aver为内容平均大小；c_i为节点缓存容量.缓存开销能够表征采样时间段内节点的负载情况.

3.3 性能评估

为验证本文设计的基于t-SNE算法的缓存容量分配机制，在全网发起了5 000次请求进行节点聚类，所有节点都能正常执行缓存替换机制(缓存空间已满)并收集50个采样时间段的流量特征信息.

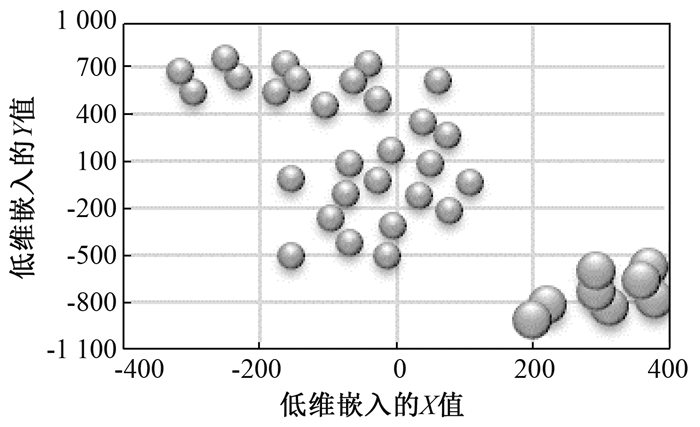
在cernet拓扑下执行本文的缓存容量分配机制得到的二维嵌入结果如图 1所示，其中每个数据点代表一个路由器节点.根据节点在网络中的相对位置可以发现，X值越大，Y值越小，节点在网络中越重要.由该图可见cernet的36个节点被聚簇为2类，含有重要节点8个，含有普通节点28个.在deltacom拓扑下执行本文的缓存容量分配机制得到的二维嵌入结果如图 2所示. deltacom中的113个节点被聚簇为4类，其中节点个数分别为6、40、30、37.

为了验证本文提出的缓存容量分配机制的性能，选取LCE(leave copy everywhere)以及Betw^[18]作为基准缓存决策机制.其中，LCE是ICN的默认缓存决策机制，它在数据包传输路径上的每个路由器节点都进行缓存；而Betw机制对LCE进行了改进，它将内容缓存在兴趣包转发路径上介数中心性最大的节点中.本文在cernet和deltacom两种网络拓扑下，将两种基准机制分别在默认等量分配和基于t-SNE算法的缓存容量分配(t-LCE、t-Betw)两种情况下进行仿真实验.在网内发起3 000个兴趣请求，并统计对应缓存命中率、路由成功率、缓存开销3个指标.实验结果如表 1所示.

从表 1中我们可以看出，在引入缓存容量分配机制后，t-LCE与t-Betw均在不同程度上提升了基准缓存机制的缓存命中率和路由成功率，且降低了网络平均缓存开销.本文提出的缓存容量分配机制基于低维嵌入的结果，为节点分配不同大小的缓存容量.cernet拓扑下，均匀分布时每个节点缓存容量为1 G，重要节点权重w₁=0.6，普通节点权重w₂=0.4，基于低维嵌入结果，每个重要节点需分配2.7 G容量，每个普通节点需分配0.5 G容量(2.7 G×8+0.5 G×28≈36 G).deltacom拓扑下，同样均匀分布时节点缓存容量为1 G，4类节点权重分别设为w₁=0.4、w₂=0.3、w₃=0.2、w₄=0.1.根据公式(8)可知，4类节点分别需要分配7.5 G、0.85 G、0.75 G、0.3 G容量(7.5 G×6+0.85 G×40+0.75 G×30+0.3 G×37≈113 G).

在两种拓扑下，本文提出的缓存容量分配机制与默认机制进行对比分析，缓存命中率提高了3%~4%，路由成功率基本维持在95%，其性能的提升与缓存决策机制本身有关.t-LCE机制对缓存命中率的提升更明显.因为从全网角度来看，尽管普通节点容量减少，但重要节点分配更多的容量后，不仅特别流行的内容副本数变化不大，还能够在重要节点缓存更多的流行内容，因此在缓存命中率指标上提升很多.t-Betw机制则在路由成功率提升方面更加明显，这是由于该机制在当前路径中的重要节点缓存内容，缓存容量分配机制为网络中相对重要的节点分配更多的缓存容量，这些节点能够响应更多的兴趣请求，因此极大提升了路由成功率.

从全网节点的平均缓存开销来看，cernet拓扑下t-LCE的平均缓存开销减少了6.3%，t-Betw的平均缓存开销减少了23.4%.deltacom拓扑下t-LCE的节点平均开销减少了13.5%，t-Betw的节点平均开销减少了17.4%.由此可见，本文提出的缓存容量分配机制在Betw上提升效果更明显，这是因为Betw对节点按照节点介数中心性进行划分，而不是像LCE机制那样对所有节点一视同仁.此外，本文提出的缓存容量分配机制，权衡了拓扑信息和流量分布，将节点按照重要程度进行划分，进而能够保证网络流量按照节点重要程度均匀分布在网内，不仅解决了部分节点负载过重的问题，还解决了少数节点缓存利用率不高的问题，从而降低了网络的整体缓存开销.

4 结束语

本文通过对现有缓存技术进行分析，提出了基于t-SNE算法的缓存容量分配机制.通过构造K-近邻表征相似性的方式改进t-SNE算法，对网络拓扑属性以及流量特征信息进行分析，基于聚类结果将有限的缓存空间合理分配给不同节点以达到平衡节点负载的目的.为验证本文方法的可行性和有效性，对算法进行了仿真实现，并与基准机制进行对比分析.从实验结果可以看出，本文设计的机制在缓存命中率、路由成功率以及缓存开销等方面具有一定的优势.下一步工作将对缓存分配机制的稳定性进行验证，进一步完善本文提出的机制.