2. 墨尔本大学 商学院 澳大利亚 维多利亚州 墨尔本 3010;
3. 郑州大学 生态与环境学院 河南 郑州 450001
2. Business School, the University of Melbourne, Victoria, Melbourne 3010, Australia;
3. School of Ecology and Environment, Zhengzhou University, Zhengzhou 450001, China
近年来,随着我国电力市场化进程加快,主动配电网智能化程度不断提高,积累了海量的用电负荷数据[1]。电力负荷曲线是描述用电负荷数据随时间变化的特性曲线[2]。利用电力负荷数据对用户群体进行划分,然后对不同子群体的用电负荷曲线进行分析有助于供电机构掌握用户行为习惯,为其在供需侧进行能效管理、制定合理的营销计划和发展战略提供帮助[3-4]。
目前关于电力负荷聚类的研究主要基于用户负荷的基本特性,主要采用基于划分、基于层次、基于密度、基于模型和基于网格的聚类算法。还有一些新的方法包括基于熵的聚类算法、自适应递归聚类算法、蚁群优化算法和社区发现方法[5-6]。谷紫文等为提高聚类质量,从信号角度出发,提出了变分模态分解和密度峰值快速搜索算法的聚类方法[4]。段秦刚等针对原有电力负荷聚类算法加入新负荷数据时,只能重新进行聚类而产生的结果不稳定问题,提出了改进的蚁群半监督聚类算法[5]。苏适等提出了一种基于密度空间聚类和引力搜索算法的用户用电模式分类模型,分析了不同类用户的用电模式及其参与需求侧响应的潜力[7]。林锦波基于聚类融合方法得到了双峰型、三峰型、平稳型以及避峰型四类用电负荷曲线,论证了聚类融合算法的效果优于单一聚类方法[8]。然而,上述无论是基于单聚类方法或是多种聚类融合方法,都是基于单一采样数据视角出发进行研究,忽视了采样数据在不同粒度视角下的内部度量信息差异。魏伟等针对上述问题提出了基于多视角网络融合的典型用电负荷模式挖掘方法,证明了使用多视角数据比单视角数据效果更好[9]。但仅挖掘出用户静态典型用电负荷模式,无法反映动态变化趋势。
为此,本文从不同粒度视角下的电力负荷数据出发,将用户看成电力社区成员,基于多视角网络融合矩阵,结合社区发现算法对用户群体进行划分,然后依据不同子社区内用户的社区属性识别各个子社区的典型用电负荷曲线,挖掘其动态模式,从而为电力系统掌握用户行为和进行电力负荷差异化调控提供理论支持。
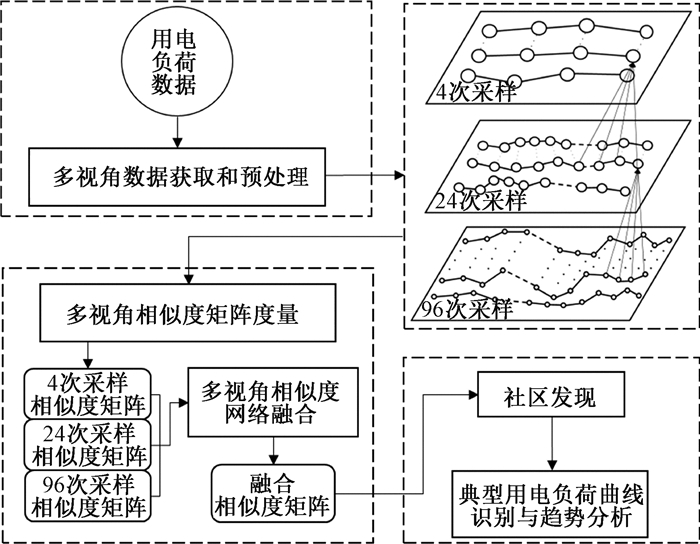
1 研究框架图 1展示了典型用电负荷曲线模式挖掘的总体研究框架,总共包含以下5个关键步骤。
|
图 1 研究框架 Fig. 1 Research framework |
1) 多视角数据获取和预处理。将一个月的用户用电负荷数据按照周一到周日进行映射,然后分别按照每天96、24和4次采样间隔获取多视角数据,并进行数据预处理。
2) 相似性度量。针对三个视角数据先采用欧氏距离进行距离度量,然后采用归一化指数相似度核方法进行相似性度量。
3) 多视角相似度网络融合。用相似度网络融合方法对三个视角下的相似度网络计算整体的相似度矩阵。
4) 社区发现。基于融合相似度矩阵,选用合适的社区发现方法将用户群体划分到不同社区。
5) 典型用电负荷曲线识别与趋势分析。以各个社区成员的介数中心性为权重,对各个社区成员进行加权,得到各个社区的典型用电负荷曲线,然后分别进行趋势分析。
2 典型用电负荷模式挖掘方法 2.1 多视角数据表示实验数据包括用户基本信息和用户每日用电负荷数据,按照每日96次采样频率,在2017年1月1日至2017年1月31日期间连续采集江苏省59家教育机构和41家房地产机构数据信息。用户基本信息数据包括用户名称、供电机构名称、电压等级、用户用电目的、用户用电总量、专变数量和专变总供电量。原始用户用电负荷数据集合表示为Dorigin,为方便后续以周为单位进行典型用电负荷曲线的趋势分析,将原始的31 d数据以平均值形式映射到周一到周日7个集合中。映射后的用户用电负荷数据集为
| $ \boldsymbol{D}_{\text {origin_week }}=\left[\begin{array}{c} d 96_{\text {monday }} \\ d 96_{\text {tuesday }} \\ \vdots \\ d 96_{\text {sunday }} \end{array}\right], d 96_{\text {monday }}, \cdots, d 96_{\text {sunday }} \in {\bf{R}}^{n \times 96}, $ |
其中:n表示用户总数。目前用电负荷采样频率为每日96次(每15分钟1次),由于数据粒度较细,导致单次采样数值变化不大。为解决单一视角下数值变化幅度过小导致的社群划分效果不佳的问题,本文考虑增加每日24次(每1小时1次)和每日4次(每6小时一次)两种粒度视角进行分析。每日96次采样数据集D96即为Dorigin_week。每日24次采样数据集D24和每日4次采样数据集D4的表示方式与D96类似,仅在列的维度上存在差异。然后对三个粒度视角数据集D96、D24、D4进行标准化处理,以消除数据间的量纲差异。
2.2 相似性度量假定有n个用户,每个用户有m次用电负荷采样数据,基于三个粒度视角下用户之间用电负荷的相似性构建三个异质图Gm=(Vm, Em), m∈{4, 24, 96},其中:节点集合Vm={u1, u2, …, un}表示每个图对应的n个用户;边集合Em={S(u1, u2), …, S(un-1, un)}表示每个图对应的用户用电负荷相似度。本文首先对三个粒度视角数据集D96、D24、D4分别采用欧氏距离度量用户ux和用户uy之间的用电负荷距离,计算公式为
| $ \begin{aligned} & d_m\left(u_x, u_y\right)=\sqrt{\sum\limits_{k=1}^m\left(u_x^k-u_y^k\right)^2}, \\ & u_x^k, u_y^k \in \boldsymbol{D}_m, m \in\{4, 24, 96\} 。\end{aligned} $ | (1) |
然后,采用指数相似度核对用户ux和用户uy之间的用电负荷相似性进行度量,计算公式为
| $ \begin{aligned} & s_m\left(u_x, u_y\right)=\exp \left(-\frac{d_m^2\left(u_x, u_y\right)}{\mu \cdot \varepsilon_m\left(u_x, u_y\right)}\right), \\ & u_{x_k}, u_{y_k} \in \boldsymbol{D}_m, m \in\{4, 24, 96\}, \end{aligned} $ | (2) |
其中:μ是一个超参数,且μ∈[0.3, 0.8];ε(ux, uy)用来消除比例缩放问题,其计算公式为
| $ \begin{aligned} & \varepsilon_m\left(u_x, u_y\right)=\left[\operatorname{mean}\left(s_m\left(u_x, \boldsymbol{N}_{u_x}\right)\right)+\right. \\ & \left.\operatorname{mean}\left(s_m\left(u_y, \boldsymbol{N}_{u_y}\right)\right)+s_m\left(u_x, u_y\right)\right] / 3, \end{aligned} $ | (3) |
其中:Nux表示用户ux的K个邻居集合;mean(sm(ux, Nux))表示用户ux与它的K个邻居特征向量间的欧氏距离平均值。根据公式(1)~(3)可以分别计算三个粒度视角数据集D96、D24、D4的相似度矩阵S96、S24和S4。
2.3 多视角相似度网络融合本文基于Wang等[10]提出的相似度网络融合方法对S96、S24和S4进行融合,基本思想为,利用存储所有样本相似度信息的矩阵Pm和存储最近K个样本相似度信息的矩阵Sm,经过融合迭代得到最终的融合相似度矩阵。相较于传统的线性加权融合方法,该方法作为一种非线性融合方法,一方面无须依赖专家经验去设置权重,另一方面在应对数据噪声和异质性问题时具有更强的鲁棒性,对于大规模数据具有更好的可扩展性[11]。
首先对相似度矩阵Sm(m∈{4, 24, 96})进行归一化操作得到Pm,计算公式为
| $ \boldsymbol{P}_m=\boldsymbol{D}_m^{-1} \cdot \boldsymbol{S}_m, m \in\{4, 24, 96\}, $ | (4) |
其中:矩阵Dm是一个对角矩阵,表示为Dm(ux, ux)=
| $ \boldsymbol{P}_m\left(u_x, u_y\right)= \begin{cases}\frac{\boldsymbol{S}_m\left(u_x, u_y\right)}{2 \sum\limits_{u_x \neq u_l} \boldsymbol{S}_m\left(u_x, u_l\right)}, & u_x \neq u_y, \\ 0.5, & u_x=u_y, \end{cases} $ | (5) |
其中:Pm(ux, uy)表示用户ux与用户uy在归一化后的相似度。最终归一化的相似度矩阵Pm存储了图Gm中所有用户的相似度信息,且满足
然后计算用户与最近邻的相似度矩阵Sm,假设用户之间距离越近则越亲密,超过一定阈值后,用户之间的亲密度为0,故用户ux与K个邻居之间的相似信息计算公式为
| $ \boldsymbol{S}_m\left(u_x, u_y\right)= \begin{cases}\frac{\boldsymbol{S}_m\left(u_x, u_y\right)}{\sum\limits_{u_k \in N_{u_x}} \boldsymbol{S}_m\left(u_x, u_K\right)}, & u_y \in \boldsymbol{N}_{u_x}, \\ 0, & \text { 其他。}\end{cases} $ | (6) |
以Pm作为初始状态矩阵,以Sm作为核矩阵进行相似度矩阵融合。三个粒度视角的初始状态矩阵为P4t=0=P4, P24t=0=P24, P96t=0=P96,融合过程迭代公式为
| $ \begin{aligned} & \boldsymbol{P}_m^{t+1}=\boldsymbol{S}_m \times\left(\sum\limits_{i \neq m} \boldsymbol{P}_i^t /( { length }(m)-1)\right) \times\left(\boldsymbol{S}_m\right)^{\mathrm{T}} \\ & m \in\{4, 24, 96\}。\end{aligned} $ | (7) |
经过t次迭代后,最终多视角相似度网络为
| $ \boldsymbol{P}_{\text {final }}=\left(\boldsymbol{P}_4^t+\boldsymbol{P}_{24}^t+\boldsymbol{P}_{96}^t\right) / 3 。$ |
社区发现旨在通过一定的方法和手段在复杂网络中划分出若干个群组。本文基于用户用电负荷相似性,采用社区发现算法对用户群体进行划分,进而识别每个社区的典型用电负荷模式。Leiden算法对社区发现领域中流行的Louvain算法进行了两处改进。1) 结合快速局部移动、智能局部移动和随机邻居移动方法使得Leiden算法的耗时比Louvain算法更短。2) 针对Louvain算法在多次迭代过程中可能产生任意连接不良或断连社区的问题,Leiden算法通过提供明确的界限能够更好地进行分区[12]。
本文使用的社区发现结果的评价指标为该领域通用的评价指标模块度,模块度指标旨在最大化社区中实际边缘数与此类边缘的预期数量之间的差异,计算公式为
| $ H=\frac{1}{2 M} \sum\limits_g\left(E_g-\gamma \frac{K_g^2}{2 M}\right), $ | (8) |
其中:Eg表示社区G中的实际边缘数;Kg表示社区g中所有节点的度之和;M表示网络G中所有边缘的总数;γ是一个大于0的分辨率参数,该参数越大则划分的社区个数越多。
2.5 典型用电负荷曲线识别通过上一节中的社区发现算法,可以将用户划分到L个社区中,进而识别每个社区的典型用电负荷曲线。传统方法是将一个社区内所有成员的每次采样电力负荷取平均值,这样可以得到m次采样电力负荷均值点,然后基于这些点绘制出一条典型用电负荷曲线。但该方式会造成严重的信息损失且容易受到极值影响,若采用加权平均的方式则需要考虑权重的设置问题。节点的介数中心性是社区的基本属性之一,表示通过该节点的最短路径数,一定程度上可以衡量这个节点的重要程度[13]。故本文以每个社区成员节点的介数中心性作为权重,与其对应的采样电力负荷值进行加权平均,最终利用加权平均的m次均值点绘制每个社区的典型用电负荷曲线,典型用电负荷曲线cE的计算公式为
| $ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;{c_\mathit{\boldsymbol{E}}} = {\mathit{\boldsymbol{B}}^{\rm{T}}} \cdot {\mathit{\boldsymbol{E}} }。\\ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {u_1^1}& \cdots &{u_1^m}\\ \vdots &{}& \vdots \\ {u_g^1}& \cdots &{u_g^m} \end{array}} \right], m = 24。\end{array} \right. $ | (9) |
假定一个社区中有g个成员,每天采样次数m为24,E为g个用户的用电负荷矩阵,B为一个社区内g个成员节点的介数中心性集合,表示为B=[b1, b2, …, bg]T。每个成员归一化介数中心性的计算公式为
| $ \left\{\begin{array}{l} b_i=b_{u_i} / \sum\limits_{i=1}^g b_{u_i}, \\ b_{u_i}=\sum\limits_{u_o \neq u_i \neq u_q \in g} \sigma_{u_o{ }_q}\left(u_i\right) / \sigma_{u_o u_q}, \end{array}\right. $ | (10) |
其中:σuouq(ui)表示通过节点ui的节点uo
识别出各个子社区的典型用电负荷曲线后,可以基于各个子社区中节点的介数中心性进一步分析。具体做法为筛选每个子社区介数中心性最高的前两个节点,对一周时间内筛选出的节点频率进行排序,选择频率最高的前3个点作为每个子社区的代表点。
3 实验及结果分析本节首先对社区发现的结果进行评价,针对社区发现结果的演化过程进行初步分析。然后结合领域知识对典型用电负荷曲线趋势变化规律进行分析。
3.1 社区发现结果评价与初步分析分别对教育机构和房地产机构用户电力负荷数据进行社区发现,在多视角相似度网络融合步骤中,选用的超参数μ为0.5,邻居个数K为10,迭代次数为10。本文采用的社区发现算法为Leiden算法,对比基线算法为Louvain算法、Walktrap算法、快速贪婪算法、边介中心性算法和特征中心性算法。表 1展示了6种社区发现算法划分的子社区个数及模块度大小。
|
|
表 1 社区发现子社区个数及模块度 Tab. 1 The number of sub-communities and modules by the community detection |
由表 1可知,对于学校和房地产用电负荷数据,使用Leiden算法进行社区发现的效果最好(表中黑体数据),其模块度大小均优于其他社区发现算法,且周一到周日每天划分的子社区个数均为3。对比教育机构和房地产机构社区发现结果的模块度,发现房地产机构的模块度数值均小于教育机构,原因可能是房地产机构用电负荷数据极差波动较大,导致社区发现任务难度提升。图 2展示了59家教育机构(图 2(a)~(g))和41家房地产机构(图 2(h)~(n))在周一至周日的社区发现结果的演化过程。节点大小表示介数中心性数值,节点越大表示该节点的介数中心性越大;边的粗细表示节点之间彼此的相似度大小,边越粗表示节点之间的相似度越高;颜色的深浅表示各个节点的子社区归属。由图 2可知,教育机构用户划分的三个子社区在持续一周的演化过程中保持了相同的社区结构,具备稳定性。整体上子社区3成员数量最多,子社区2成员数量其次,子社区1成员数量最少。房地产机构划分的3个子社区呈现出两种模式,且除周日外子社区的界限都十分明晰。整体上子社区1成员数量最多,子社区2成员数量其次,子社区3成员数量最少。

|
图 2 教育机构与房地产机构社区发现结果演化过程 Fig. 2 The evolutionary process of the educational and real estate organization institution by community detection |
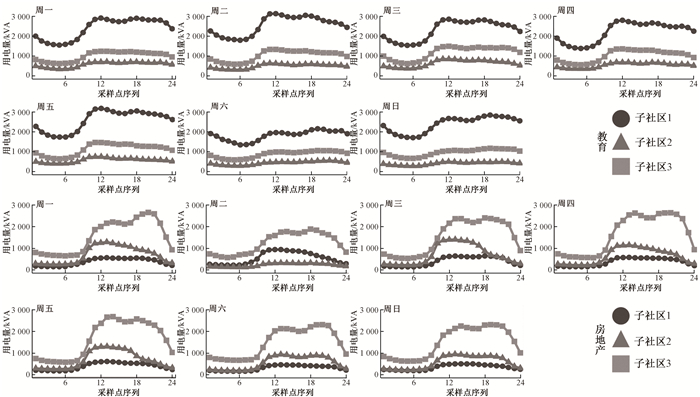
图 3展示了59家教育机构与41家房地产机构典型用电负荷趋势曲线。结合用户基本信息数据进行分析。
|
图 3 教育机构与房地产机构典型用电负荷趋势曲线 Fig. 3 Typical power load trend curves of educational institution and real estate organization |
1) 教育机构典型用电负荷趋势曲线分析。教育机构各个子社区的代表点分别为:子社区1为南京大学、南京旅游学院和河海大学;子社区2为江苏健康职业学院、南京铁道职业技术学院和江苏警官学院;子社区3为南京工业大学、南京财经大学和南京晓庄学院。在教育机构社区发现结果演化过程的分析中可知教育机构的社区发现结果具备稳定性,图 3的结果验证了这一观点。除此之外,在一周时间里,子社区1的用电负荷量和峰值波动最大,其次是子社区3,最后是子社区2;子社区1的用电负荷量远高于其他两个子社区。出现上述结果的原因可能是子社区1的成员所属的学校层次水平和办学规模较高,子社区3其次,子社区2最低,因而上述教育机构两种属性的差异导致了典型用电负荷曲线趋势的差异性。
2) 房地产机构典型用电负荷趋势曲线分析。房地产机构各个子社区的代表点分别为:子社区1为南京天悦置业投资顾问有限公司、南京万尚城有限公司和南京高科股份有限公司;子社区2为南京红太阳房地产开发有限公司、银城地产集团股份有限公司、南京华欧舜都置业有限公司;子社区3为南京新宇房产开发有限公司、南京凯润房地产有限公司、江苏徐矿置业有限公司。在房地产机构社区发现结果演化过程中有两种模式:周一、周二、周三、周五和周六;周四和周日。这与房地产机构典型用电负荷趋势曲线的两种模式(周二;除周二之外)并没有完全对应,表明社区发现结果的演化过程与典型用电负荷曲线趋势变化之间可能不存在显著的相关关系。在图 3中展示的房地产机构典型用电负荷趋势曲线中:在整体上子社区3的用电负荷量与峰值波动最高,存在午高峰和晚高峰用电负荷负载较高的情况;子社区2在一周时间里的典型用电负荷趋势大致呈现出工作日(周一至周五)和双休日(周六及周日)两种模式,除周二外的工作日用电负荷量呈现单峰分布情况,且整体数值较高,而双休日的用电负荷量呈现双峰分布情况,且整体数值比工作日更低;子社区1在一周时间里的用电负荷趋势变化不大,相对稳定。3个子社区的用电负荷相关属性包括用户容量、专变数量和专变容量合计。子社区1~3的用户容量均值分别为12506.7、21466.7和28 800 kVA;专变数量均值分别为4.7、6.7和11.3个;专变容量合计均值分别为6253.3、10733.3和17000.6 kVA。三个子社区在用户容量、专变数量和专变容量合计三个属性均值上,均为子社区3>子社区2>子社区1。与房地产机构典型用电负荷趋势曲线的整体趋势保持一致,因此可以考虑利用以上三个用电负荷属性作为各个子社区典型用电负荷曲线的判别因素。
4 结论本文针对当前研究中忽视了多视角电力负荷采样数据的问题,提出了一种基于多视角数据与社区发现的典型用电负荷模式挖掘方法。并利用江苏省59家教育机构和41家房地产机构的用电负荷真实数据进行实验,结果表明本文提出的方法能够识别出各个子社区的典型用电负荷曲线,并且能够结合用户自身的属性信息对典型用电负荷曲线的趋势进行进一步的解释与分析。对于教育机构,各个子社区的典型用电负荷曲线趋势具备稳定性,可能与教育机构用电行为较为稳定且单一有关。对于供电机构而言,可以根据教育机构所属学校的层次水平及办学规模进行差异化供电。对于房地产机构,可以通过用户容量、专变数量和专变容量3个属性来大致判断其典型用电负荷曲线的数值大小。3个子社区呈现出不同的峰值分布模式,供电机构可以根据对应的模式进行错峰供电,用削峰填谷等措施进行供电,为用户提供个性化的供电服务。
| [1] |
陈俊艺, 丁坚勇, 田世明, 等. 基于改进快速密度峰值算法的电力负荷曲线聚类分析[J]. 电力系统保护与控制, 2018, 46(20): 85-93. CHEN J Y, DING J Y, TIAN S M, et al. An improved density peaks clustering algorithm for power load profiles clustering analysis[J]. Power system protection and control, 2018, 46(20): 85-93. (  0) 0) |
| [2] |
方茂益, 孙志杰, 周国鹏, 等. 基于FCM配电侧典型电力日负荷曲线分类研究[J]. 华北电力技术, 2016(11): 15-19. FANG M Y, SUN Z J, ZHOU G P, et al. Typical power daily load classification based on fuzzy C-means clustering algorithm[J]. North China electric power, 2016(11): 15-19. (  0) 0) |
| [3] |
朱祥和. 考虑气象因素的短期负荷预测模型研究[J]. 数学的实践与认识, 2018, 48(3): 131-143. ZHU X H. Study on short-term load forecasting model considering meteorological factors[J]. Mathematics in practice and theory, 2018, 48(3): 131-143. (  0) 0) |
| [4] |
谷紫文, 李鹏, 郎恂, 等. 基于变分模态分解和密度峰值快速搜索的电力负荷曲线可控聚类模型[J]. 电力系统保护与控制, 2021, 49(8): 118-127. GU Z W, LI P, LANG X, et al. A controllable clustering model of the electrical load curve based on variational mode decomposition and fast search of the density peak[J]. Power system protection and control, 2021, 49(8): 118-127. (  0) 0) |
| [5] |
段秦刚, 王浩浩, 伍子东, 等. 基于改进蚁群算法的电力负荷半监督聚类[J]. 电力建设, 2020, 41(10): 81-89. DUAN Q G, WANG H H, WU Z D, et al. Research on power load semi-supervised clustering based on improved ant colony algorithm[J]. Electric power construction, 2020, 41(10): 81-89. (  0) 0) |
| [6] |
魏震波, 关翔友, 刘梁豪. 电网社区结构发现方法及其应用综述[J]. 电网技术, 2020, 44(7): 2600-2609. WEI Z B, GUAN X Y, LIU L H. Overview of power community structure discovery algorithms and their application in power grid analysis[J]. Power system technology, 2020, 44(7): 2600-2609. (  0) 0) |
| [7] |
苏适, 李康平, 严玉廷, 等. 基于密度空间聚类和引力搜索算法的居民负荷用电模式分类模型[J]. 电力自动化设备, 2018, 38(1): 129-136. SU S, LI K P, YAN Y T, et al. Classification model of residential power consumption mode based on DBSCAN and gravitational search algorithm[J]. Electric power automation equipment, 2018, 38(1): 129-136. (  0) 0) |
| [8] |
林锦波. 聚类融合与深度学习在用电负荷模式识别的应用研究[D]. 广州: 华南理工大学, 2014. LIN J B. Application of recognition model for power load in cluster ensemble and deep learning[D]. Guangzhou: South China University of Technology, 2014. (  0) 0) |
| [9] |
魏伟, 李永胜, 程逍, 等. 基于多视角网络融合的典型用电负荷模式挖掘[J]. 沈阳工业大学学报, 2022, 44(3): 248-254. WEI W, LI Y S, CHENG X, et al. Mining for typical power load modes based on multi-view network fusion[J]. Journal of Shenyang university of technology, 2022, 44(3): 248-254. (  0) 0) |
| [10] |
WANG B, MEZLINI A M, DEMIR F, et al. Similarity network fusion for aggregating data types on a genomic scale[J]. Nature methods, 2014, 11(3): 333-337. (  0) 0) |
| [11] |
CHEN J F, SUN L L, GUO C H, et al. A fusion framework to extract typical treatment patterns from electronic medical records[J]. Artificial intelligence in medicine, 2020, 103: 101782. (  0) 0) |
| [12] |
TRAAG V A, WALTMAN L, VAN ECK N J. From Louvain to Leiden: guaranteeing well-connected communities[J]. Scientific reports, 2019, 9: 5233. (  0) 0) |
| [13] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical review E, Statistical, nonlinear, and soft matter physics, 2004, 69(2): 026113. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


