2. 北京航空航天大学 自动化科学与 电气工程学院 北京 100191;
3. 中国科学院 空间应用工程与技术中心 北京 100094
2. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China;
3. Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China
灰色关联分析理论以研究“小样本,贫信息”的数据系列相关性大小为主要内容,为不确定性系统的建模、评价与决策提供了有利工具.传统灰色关联分析模型是依据比较序列与参考序列的曲线几何相似程度进行度量的.事实上,关联度大小不仅与曲线相似程度密切相关,也与曲线之间的接近程度紧密联系.目前,不同学者从几何、积分、分数阶导数、插值等不同角度定义了多种不同的改进型灰色关联分析模型[1-7].文献[1]构建了绝对灰色关联度, 该模型满足偶对称性, 且计算相对简便.文献[2]基于数据序列相似性与相近性视角构建了新型灰色关联分析模型,但该模型对于走势不一致的两组数据会出现灰色关联度为1的情况.文献[3]指出关联度取值随分辨系数变化而变化,从而造成关联度取值唯一性不满足或关联度不满足对称性等问题.文献[4]利用光滑性与逼近效果较好的三次样条插值函数逼近序列数据改进了灰色绝对关联度, 提高了逼近精度.文献[5]利用梯形求积法建立了序列数据折线面积基础上的灰色预测模型.文献[6]采用Caputo型分数阶导数的记忆性改进灰色预测模型.文献[7]提出了基于改进灰色关联度模型的综合一致性检验方法.这些工作都促进了灰色系统理论的发展.
灰色相似关联度与接近关联度是建立在两组序列数据所围图形面积基础之上的[2, 8],但当两组序列数据存在振荡情况时表现的并不准确,当一组序列数据在另一组序列数据之上与之下的面积相等时,关联度为1.本文将利用分段二次Lagrange插值完成对序列数据的逼近,通过引入绝对值表示所围面积的改进型灰色相似关联度与灰色接近关联度模型.结合微元法与梯形法的计算,客观地反映序列数据的相似性与接近性.
1 灰色相似关联度与接近关联度的改进 1.1 基于面积的灰色相似关联度与接近关联度的定义与计算定义1[2] 设系统第i组与第j组序列数据为Xi=(xi(1), xi(2), …, xi(n)), Xj=(xj(1), xj(2), …, xj(n)),它们的始点零化像分别为Xi0=(xi0(1), xi0(2), …, xi0(n)),Xj0=(xj0(1), xj0(2), …, xj0(n)),其中:i, j表示序列标号;xi0(k)=xi(k)-xi(1), xj0(k)=xj(k)-xj(1),k=1, 2, …, n,且n≥3.
定义2 设fi(t)是第i组序列数据Xi的逼近函数, fj(t)是第j组序列数据Xj的逼近函数, t∈[1, n],fi(t)与fj(t)的始点零化像分别为fi0(t)与fj0(t),其中:fi0(t)=fi(t)-fi(1),fj0(t)=fj(t)-fj(1),fi(t)与fj(t)可以采用拟合或插值的方法对原始序列数据进行逼近.
当使用分段线性Lagrange插值逼近原始序列数据时会出现光滑性较差, 且精度不高的问题, 而三次样条插值又相对较复杂, 故为了简化计算, 提高计算精度, 下面采用分段二次Lagrange插值.
定义3[9] 对于如定义1所给的第i组序列数据Xi,任取相邻节点k-1, k, k+1,以[k-1, k+1]作为插值区间构造分段二次Lagrange插值函数,
| $ {f_{ik}}\left( t \right) = {x_i}\left( {k - 1} \right){l_{k - 1}}\left( t \right) + {x_i}\left( k \right){l_k}\left( t \right) + {x_i}\left( {k + 1} \right){l_{k + 1}}\left( t \right), $ |
其中:
根据定义3整理出序列数据Xi, Xj的分段二次Lagrange插值函数的整体形式.
当n≥3, 且n=2g+1, g∈Z+时,
| $ {f_i}\left( t \right) = \sum\limits_{k = 2}^{2g} {{\mathit{\delta }_k}} {f_{ik}}\left( t \right);{f_i}\left( t \right) = \sum\limits_{k = 2}^{2g} {{\mathit{\delta }_k}} {f_{ik}}\left( t \right);{\mathit{\delta }_k} = \left\{ {\begin{array}{*{20}{c}} {1, }&{t \in \left[{k-1, k + 1} \right]}\\ {0, }&{t \notin \left[{k-1, k + 1} \right]} \end{array}} \right.. $ | (1) |
当n≥4, 且n=2g, g∈Z+时,
| $ \begin{array}{*{20}{l}} {{f_i}\left( t \right) = \sum\limits_{k = 2}^{2g - 2} {{\mathit{\delta }_k}} {f_{ik}}\left( t \right) + \mathit{\delta }{f_i}_{\left( {2g - 1} \right)}\left( t \right);{f_j}\left( t \right) = \sum\limits_{k = 2}^{2g - 2} {{\mathit{\delta }_k}} {f_{jk}}\left( t \right) + \mathit{\delta }{f_j}_{\left( {2g - 1} \right)}\left( t \right);}\\ {{\mathit{\delta }_k} = \left\{ {\begin{array}{*{20}{c}} {1, }&{t \in \left[{\begin{array}{*{20}{c}} {k-1, }&{k + 1} \end{array}} \right]}\\ {0, }&{t \notin \left[{\begin{array}{*{20}{c}} {k-1, }&{k + 1} \end{array}} \right]} \end{array}} \right.;\mathit{\delta } = \left\{ {\begin{array}{*{20}{c}} {1, }&{t \in \left[{\begin{array}{*{20}{c}} {n-1, }&n \end{array}} \right]}\\ {0, }&{t \notin \left[{\begin{array}{*{20}{c}} {n-1, }&n \end{array}} \right]} \end{array}} \right..} \end{array} $ | (2) |
其中
| $ {f_{jk}}\left( t \right) = {x_j}\left( {k - 1} \right){l_{k - 1}}\left( t \right) + {x_j}\left( k \right){l_k}\left( t \right) + {x_j}\left( {k + 1} \right){l_{k + 1}}\left( t \right) $ |
为Xj在t∈[k-1, k+1]时的分段二次Lagrange插值函数, 插值基函数lk-1(t), lk(t), lk+1(t)定义同上, k=2, 4, 6, …,n, 且n≥3.
在得到分段二次Lagrange插值函数fi(t)与fj(t)的基础上, 再按照定义2分别对fi(t)与fj(t)进行始点零化像操作后可以获得fi0(t)与fj0(t).
定义4 设
| $ {\alpha _{ij}} = \frac{1}{{1 + \mathit{\Delta } {s_{ij}}}} $ | (3) |
为序列数据Xi与Xj基于面积的灰色相似关联度, 称
| $ {\mathit{\beta }_{ij}} = \frac{1}{{1 + \mathit{\Delta }{S_{ij}}}} $ | (4) |
为序列数据Xi与Xj基于面积的灰色接近关联度.
注:Δsij表示fi0(t)与fj0(t)对应曲线与直线t=1, t=n所围图形的面积, ΔSij表示fi(t)与fj(t)对应曲线与直线t=1, t=n所围图形的面积.
对于量纲相同的两组原始序列数据Xi与Xj,基于面积的灰色相似关联度αij可以表征Xi与Xj对应曲线的相似程度, Xi与Xj越相似, fi(t)与fj(t)也就越相似, 则fi0(t)与fj0(t)重合的可能性就越大, Δsij取值越接近于0, αij取值就越接近1.基于面积的灰色接近关联度βij可以表征Xi与Xj对应曲线的接近程度, Xi与Xj越接近, fi(t)与fj(t)也就越接近, 则ΔSij取值越接近于0, βij取值就越接近1.构建的基于面积的灰色相似关联度与接近关联度均充分考虑了原始序列数据在始点零化处理之前与之后各自在平面直角坐标系中所围封闭图形的面积大小的差异性.对于定义4中的Δsij与ΔSij,用两种近似数值计算方法.
1) 微元法
| $ \mathit{\Delta }{s_{ij}} = \int_1^n {\left| {f_i^0\left( t \right) - f_j^0\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \sum {\left| {f_i^0\left( t \right) - f_j^0\left( t \right)} \right|} \Delta t, $ | (5) |
| $ \mathit{\Delta }{S_{ij}} = \int_1^n {\left| {{f_i}\left( t \right) - {f_j}\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \sum {\left| {{f_i}\left( t \right) - {f_j}\left( t \right)} \right|} \Delta t, $ | (6) |
其中Δt为采样步长.
2) 梯形求积法(简称梯形法)
| $ \mathit{\Delta }{s_{ij}} = \int_1^n {\left| {f_i^0\left( t \right) - f_j^0\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \frac{1}{2}\left| {f_i^0\left( n \right) - f_j^0\left( n \right)} \\\right|\Delta t{\rm{ + }}\sum\limits_{k = 1}^{m - 1} {\left| {f_i^0\left( {1{\rm{ + }}k\Delta t} \right) - f_j^0\left( {1{\rm{ + }}k\Delta t} \right)} \right|} \Delta t, $ | (7) |
| $ \begin{array}{l} \mathit{\Delta }{S_{ij}} = \int_1^n {\left| {{f_i}\left( t \right) - {f_j}\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \frac{1}{2}\left| {f_i^0\left( n \right) - f_j^0\left( n \right)} \right|\Delta t{\rm{ + }}\frac{1}{2}\left| {f_i^0\left( 1 \right) - f_j^0\left( 1 \right)} \right|\Delta t{\rm{ + }}\\ \sum\limits_{k = 1}^{m - 1} {\left| {f_i^0\left( {1{\rm{ + }}k\Delta t} \right) - f_j^0\left( {1{\rm{ + }}k\Delta t} \right)} \right|} \Delta t, \end{array} $ | (8) |
其中:Δt为采样步长, m=(n-1)/Δt.
证明 设Xi与Xj是如定义1所给出的两个不同序列数据, fi(t)与fj(t)是对应的分段二次Lagrange插值函数.
a) 当始点零化像fi0恒在fj0的一侧时
| $ \mathit{\Delta }{s_{ij}} = \int_1^n {\left| {f_i^0\left( t \right) - f_j^0\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \sum\limits_{k = 0}^{m - 1} {\mathit{\Delta} s_{_{ij}}^k}, $ | (9) |
其中:Δsijk为第k个小梯形的面积, k=0, 1, …, m;Δt为采样步长; m=(n-1)/Δt.因为
| $ \begin{array}{*{20}{l}} {\mathit{\Delta} s_{ij}^k \approx \frac{1}{2}\left| {f_i^0\left( {1 + \mathit{k}\Delta t} \right) - f_j^0\left( {1 + k\Delta t} \right)} \right|\Delta t + \frac{1}{2}\left| {f_i^0\left( {1 + k\Delta t + \Delta t} \right) - f_j^0\left( {1 + k\Delta t + \Delta t} \right)} \right|\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta t, }f_i^0\left( 1 \right) = {f_i}\left( 1 \right) - {f_i}\left( 1 \right) = 0, f_j^0\left( 1 \right) = {f_j}\left( 1 \right) - {f_j}\left( 1 \right) = 0, } \end{array} $ |
代入(9) 即得公式(7).同理当fi(t)恒在fj(t)的一侧时, 使用梯形求积公式可证明公式(8).
b) 当始点零化像fi0与fj0存在除(1, 0) 外的交点(1+k0Δt, x)时, 则存在某个k=k0,使得fi0(1+k0Δt)=fj0(1+k0Δt)=x,k=0, 1, …, m,则
| $ \mathit{\Delta }{s_{ij}} = \int_1^n {\left| {f_i^0\left( t \right) - f_j^0\left( t \right)} \right|} {\rm{d}}\mathit{t} \approx \sum {\mathit{\Delta} s_{ij}^k} + \mathit{\Delta} s_{ij}^{{k_0} - 1} + \mathit{\Delta} s_{ij}^{{k_0}}, $ | (10) |
其中:Δsijk为第k个小梯形的面积, k=0, 1, …, m; k≠k0, k≠k0-1; m=(n-1)/Δt,Δt为采样步长; Δsijk0-1, Δsijk0为三角形面积.因为k≠k0, k≠k0-1时,
| $ \mathit{\Delta} s_{ij}^k \approx \frac{1}{2}\left| {f_i^0\left( {1 + k\Delta t} \right) - f_j^0\left( {1 + k\Delta t} \right)} \right|\\\Delta t + \frac{1}{2}\left| {f_i^0\left( {1 + k\Delta t + \Delta t} \right) - f_j^0\left( {1 + k\Delta t + \Delta t} \right)} \right|\Delta t, $ |
又由|fi0(1+k0Δt)-fj0(1+k0Δt)|=0,可知
| $ \begin{array}{l} \mathit{\Delta} s_{ij}^{{k_0}} = \frac{1}{2}\left| {f_i^0\left( {1 + {k_0}\Delta t + \Delta t} \right) - f_j^0\left( {1 + {k_0}\Delta t + \Delta t} \right)} \right|\\\Delta t + \frac{1}{2}\left| {f_i^0\left( {1 + {k_0}\Delta t} \right) - f_j^0\left( {1 + {k_0}\Delta t} \right)} \right|\Delta t, \\ \mathit{\Delta} s_{ij}^{{k_0} - 1} = \frac{1}{2}\left| {f_i^0\left( {1 + {k_0}\Delta t - \Delta t} \right) - f_j^0\left( {1 + {k_0}\Delta t - \Delta t} \right)} \right|\\\Delta t + \frac{1}{2}\left| {f_i^0\left( {1 + {k_0}\Delta t} \right) - f_j^0\left( {1 + {k_0}\Delta t} \right)} \right|\Delta t. \end{array} $ |
代入式(10) 化简即得公式(7).同理当fi(t)与fj(t)存在交点时, 使用梯形求积公式亦可证明公式(8).
1.2 基于面积的灰色相似关联度与接近关联度的相关性质定理1 基于面积的灰色相似关联度为
证明 1) 规范性.显然Δsij≥0, ΔSij≥0,故0 < αij≤1, 0 < βij≤1,当且仅当Δsij=0时,αij=1,ΔSij=0时,βij=1.
2) 接近性.由1) 可知,显然成立.
3) 偶对称性.对于X={Xi, Xj},显然有fi0(t)-fj0(t)=fj0(t)-fi0(t),Δsij=Δsji,fi(t)-fj(t)=fj(t)-fi(t),ΔSij=ΔSji,故αij=αji,βij=βji.
定理2 在平面直角坐标系下, 当始点零化像Xi0恒在Xj0的一侧时, αij≈εij,当序列数据Xi恒在Xj的一侧时, βij≈ρij.其中εij,ρij分别为文献[2]所定义的灰色相似关联度与灰色接近关联度,
| $ {\varepsilon _{ij}} = \frac{1}{{1 + \left| {{s_i} - {s_j}} \right|}};{s_i} - {s_j} = \int_1^n {\left( {x_t^0\left( t \right) - x_j^0\left( t \right)} \right)} {\rm{d}}\mathit{t, } $ | (11) |
| $ {\rho _{ij}} = \frac{1}{{1 + \left| {{S_i} - {S_j}} \right|}};{S_i} - {S_j} = \int_1^n {\left( {{x_i}\left( t \right) - {x_j}\left( t \right)} \right)} {\rm{d}}\mathit{t}\mathit{.} $ | (12) |
证明 当始点零化像Xi0恒在Xj0的一侧时, 因
对于非1-时距序列可以采用相应变换转化为1-时距序列, 故假设下面讨论的均是1-时距序列[2], 并且要求序列数据的长度是一致的, 而当序列长度不一致时可以采用分层逐次均值填补空缺[2].
例1 设序列数据X1=(x1(1), x1(2), …, x1(7))=(0.91, 0.97, 0.90, 0.93, 0.91, 0.93, 0.95),X2=(x2(1), x2(2), …, x2(7))=(0.60, 0.68, 0.61, 0.62, 0.63, 0.64, 0.65),X3=(x3(1), x3(2), …, x3(7))=(0.82, 0.86, 0.90, 0.89, 0.88, 0.87, 0.86),X1, X2, X3均是1-时距序列, n=7,试求X2, X3与X1三者之间基于面积的灰色相似关联度α12, α13, α23与灰色接近关联度β12, β13, β23,要求给出与文献[2]方法、基于微元法的相似与接近关联度、基于梯形求积法的相似与接近关联度(简称梯形法)的对比结果.
解 1) 由于n=7,故首先按照公式(1),计算X1, X2, X3的分段二次Lagrange插值曲线得f1(t), f2(t), f3(t),见图 1.
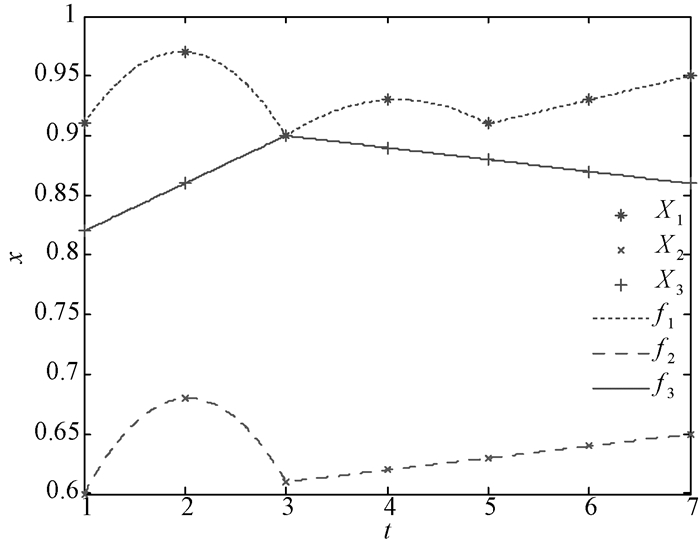
|
图 1 原数据与Lagrange插值曲线 Figure 1 Original data and Lagrange interpolation curves |
2) 计算f1(t), f2(t), f3(t)的始点零化像f10(t), f20(t), f30(t),为了与其他方法进行对比, 也一并算出X1, X2, X3的始点零化像X10, X20, X30得, fi0(t)=fi(t)-fi(1), i=1, 2, 3. X10=(x10(1), x10(2), …, x10(7))=(0, 0.06, -0.01, 0.02, 0, 0.02, 0.04),X20=(x20(1), x20(2), …, x20(7))=(0, 0.08, 0.01, 0.02, 0.03, 0.04, 0.05),X30=(x30(1), x30(2), …, x30(7))=(0, 0.04, 0.08, 0.07, 0.06, 0.05, 0.04),其中f10(t), f20(t), f30(t)是f1(t), f2(t), f3(t)的始点零化像, 也是X10, X20, X30的分段二次Lagrange插值曲线, 如图 2所示.
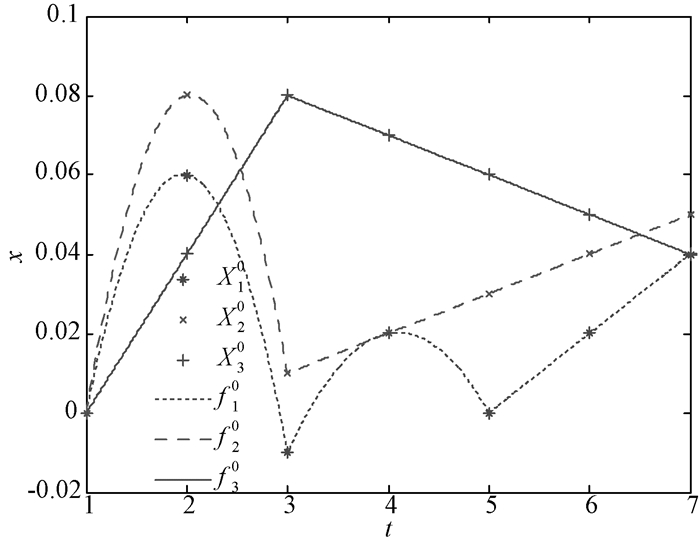
|
图 2 始点零化像与Lagrange插值曲线 Figure 2 Initial point zero image and Lagrange interpolation curves |
3) 根据微元法与梯形法给定的公式分别计算Δsij, ΔSij.采用微元法由公式(5) 计算Δsij,采样步长Δt=0.01, 由公式(6) 计算ΔSij,得Δs12≈0.104 8,Δs13≈0.266 1,Δs23≈0.215 6,ΔS12≈2.061 6,ΔS13≈0.419 3,ΔS23≈1.642 3.
采用梯形求积法由公式(7) 计算Δsij,由公式(8) 计算ΔSij,得
Δs12≈0.104 9,Δs13≈0.266 1,Δs23≈0.215 6,ΔS12≈2.058 0,ΔS13≈0.418 2,ΔS23≈1.639 7.
4) 最后代入公式(3) 和(4) 计算出基于面积的灰色相似关联度与灰色接近关联度, 结合文献[2]的方法给出对序列数据两两比较的3种结果, 见表 1.
|
|
表 1 比较结果 Table 1 Comparison of results |
使用微元法得灰色相似关联度与灰色接近关联度为:
| $ {\alpha _{12}} = 0.905\;1, {\alpha _{13}} = 0.789\;8, {\alpha _{23}} = 0.822\;7, $ |
| $ {\mathit{\beta }_{12}} = 0.326\;6, {\mathit{\beta }_{13}} = 0.704\;6, {\mathit{\beta }_{23}} = 0.378\;5. $ |
使用梯形求积法得灰色相似关联度与灰色接近关联度为α12=0.905 1,α13=0.789 9,α23=0.822 7,β12=0.327 0,β13=0.705 1,β23=0.378 8.
上述两种方法的计算结果表明, X1, X2, X3中的X1, X2最相似, X2, X3的相似程度次之, 而X1, X3的相似程度最低; X1, X3最接近, X2, X3的接近程度次之, 而X1, X2的接近程度最低.对于本算例, 三种方法给出的序列数据的相似程度和接近程度的排序是一致的.
例2 设序列数据
| $ \begin{array}{l} {\mathit{X}_1} = \left( {{x_1}\left( 1 \right), {x_1}\left( 2 \right), \cdots, {x_1}\left( 5 \right)} \right) = \left( {1, 2, 3, 4, 5} \right), \\ {\mathit{X}_2} = \left( {{x_2}\left( 1 \right), {x_2}\left( 2 \right), \cdots, {x_2}\left( 5 \right)} \right) = \left( {1, 1, 3, 5, 5} \right), \end{array} $ |
试给出X1, X2基于分段二次Lagrange插值微元法、梯形法与刘氏法的灰色相似关联度与接近关联度.
解 本算例的计算与上例是一样的, 采用上例相同的4步操作可得X1, X2基于分段二次Lagrange插值微元法、梯形法的结果,见表 2.显然, 微元法和梯形法的结果是合理的, 而刘氏法的结果是不合理的, 因为差异较大数据的关联度是不可能取1的.原序列数据与分段二次Lagrange插值曲线见图 3.
|
|
表 2 比较结果 Table 2 Comparison of results |
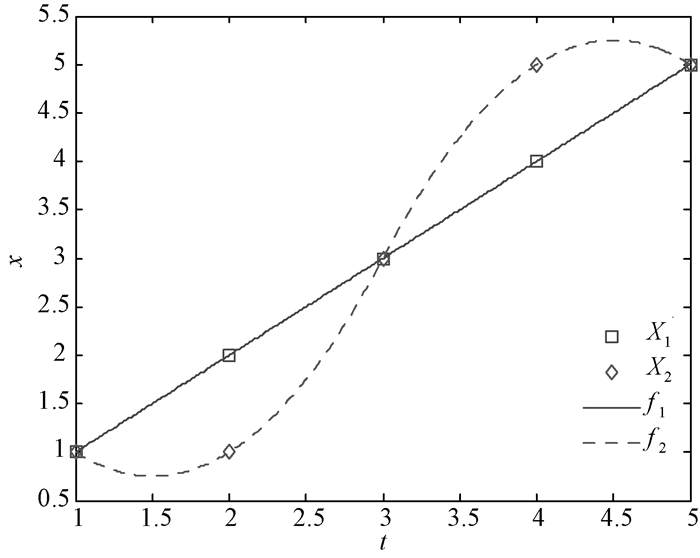
|
图 3 原数据与分段二次Lagrange插值曲线 Figure 3 Original data and piecewise quadratic Lagrange interpolation curves |
建立不同序列数据的分段二次Lagrange插值, 尽可能以一种简单的方式逼近序列数据, 基于序列数据被逼近曲线与t=1, t=n所围的图形面积,构建了微元法与梯形法两种计算灰色相似关联度与灰色接近关联度的改进算法, 使得灰色关联度的计算更能反映数据间的几何位置关系.改进模型克服了原有灰色相似关联度与接近关联度不能客观反映振荡序列相似性与接近性的弊端, 是对原有模型的有效拓展.通过算例证明了本文所提出的基于面积的两种方法是有效的.当数据较多, 信息包含较多时, 基于分段二次Lagrange插值建立的逼近曲线将具有较高的逼近精度, 随之建立的灰色相似关联度与接近关联度模型也将具有较高的评估精度.
| [1] |
LIU S, FANG Z, LIN Y. A new definition for the degree of grey incidence[J]. Grey systems theory and application, 2005, 7(2): 8-18. (  0) 0) |
| [2] |
刘思峰, 谢乃明, FORRESTJ. 基于相似性和接近性视角的新型灰色关联分析模型[J]. 系统工程理论与实践, 2010, 30(5): 881-887. DOI:10.12011/1000-6788(2010)5-881 (  0) 0) |
| [3] |
刘勇, 刘思峰, FORRESTJ. 一种新的灰色绝对关联度模型及其应用[J]. 中国管理科学, 2010, 20(5): 173-177. (  0) 0) |
| [4] |
陈勇明, 张明. 灰色样条绝对关联度模型[J]. 系统工程理论与实践, 2015, 35(5): 1304-1310. DOI:10.12011/1000-6788(2015)5-1304 (  0) 0) |
| [5] |
蒋诗泉, 刘思峰, 刘中侠, 等. 基于面积的灰色关联决策模型[J]. 控制与决策, 2015, 30(4): 685-690. (  0) 0) |
| [6] |
吴利丰, 刘思峰, 姚立根. 含Caputo型分数阶导数的灰色预测模型[J]. 系统工程理论与实践, 2015, 35(5): 1311-1316. DOI:10.12011/1000-6788(2015)5-1311 (  0) 0) |
| [7] |
胡玉伟, 马萍, 杨明, 等. 基于改进灰色关联分析的仿真数据综合一致性检验方法[J]. 北京理工大学学报(自然科学版), 2013, 33(7): 711-715. (  0) 0) |
| [8] |
刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2014.
(  0) 0) |
| [9] |
施吉林, 张宏伟, 金光日. 计算机科学计算[M]. 北京: 高等教育出版社, 2005.
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49

