2. 河南中烟工业有限责任公司 河南 郑州 450016;
3. 广西中烟工业有限责任公司 广西 南宁 530000
2. China Tobacco Henan Industrial Co. Ltd., Zhengzhou 450016, China;
3. China Tobacco Guangxi Industrial Co. Ltd., Nanning 530000, China
图像匹配是模式识别、图像分析、机器学习和计算机视觉研究中的一个重要领域,如视觉的跟踪和人脸识别,车辆的无人驾驶等[2-4]。根据已知模板在参考图像中搜索合适的子图像的过程称为模板匹配[1]。实现模板匹配主要分为基于强度的方法和基于特征的方法[5], 然而, 这两种匹配方法大多采用的是遍历式搜索进行匹配,虽然具有较高的鲁棒性和较好的匹配结果,但计算量较大,特别是当模板规模增加时。为此张焕龙等[6]提出每次只增加和减少与步长相关信息的增量式方法,这使得遍历式匹配方法的计算量大大降低。李强等[7]通过比较图像各部分编码值的方法,降低了灰度匹配算法的时间复杂度。唐永鹤等[8]提出通过特征描述算子的方法来减少计算量,提高匹配效率。然而这些改进仍保存着遍历式搜索的弊端,即存在大量的匹配点对。
近年来,许多启发式方法被引入到基于强度的匹配中。智能优化算法在解决问题时,通常采用非遍历式的方法,这种特性使得算法在鲁棒性不变的前提下,计算成本大大降低。周美茹[9]利用惯性权重因子的自适应个体迁徙策略使得参数有所减少,改善了细菌觅食算法中由于迁徙概率和随机迁移的固定而引起的最优解“逃逸”问题。张焕龙等[10]利用混合模拟退火和蚁狮优化算法增强了算法寻找最优解的能力,并应用于图像匹配中,使匹配精度得以提升。王斐等[11]利用樽海鞘优化算法参数少、易于调节的特点,首次将其与图像匹配结合起来,然而由于樽海鞘优化算法在解决复杂问题时易陷入局部最优的局限性,使得匹配精度有待提升。彭健等[12]利用混合离散余弦变换(DTC)和鸡群算法,使得算法的收敛速度和精度得以提升,并在图像匹配上取得了一定的优势。
虽然以上算法在精度上得以提升,但在实际应用中存在调节参数多、不易操作等问题。鹈鹕优化算法[13]具有参数少,结构简单等优点。但传统的鹈鹕优化算法在处理多峰值函数问题时易陷入局部最优,针对这个问题,提出了一种基于质量扰动的鹈鹕优化算法,降低了算法在处理多峰值问题时易陷入局部最优的概率,将其运用到图像匹配问题中,改善了传统群优化算法调节参数多、不易操作等问题。
1 鹈鹕优化算法鹈鹕优化算法是一种模拟鹈鹕捕食的算法。鹈鹕在确定猎物位置后,从10~20 m的高度俯冲下来捕食,它们在水面上展开翅膀,迫使鱼进入浅水区,这是一个捕捉它们的好方法[14],基于此捕食过程,提出了POA算法。
1.1 种群初始化根据搜索区域的边界,随机生成POA初代种群的位置,所用公式为
| $ \begin{aligned} & x_{i, j}=l b_j+{rand}\left(u b_j-l b_j\right), i=1, 2, \cdots, N, j=1, 2, \cdots, D_{\text {dim }}, \\ & \boldsymbol{X}=\left[\begin{array}{c} \vec{X}_1 \\ \vdots \\ \vec{X}_i \\ \vdots \\ \vec{X}_N \end{array}\right]_{N * D_{\text {dim }}}=\left[\begin{array}{ccccc} x_{1, 1} & \cdots & x_{1, j} & \cdots & x_{1, D_{\text {dim }}} \\ \vdots & & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, D_{\text {dim }}} \\ \vdots & & \vdots & & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, D_{\text {dim }}} \end{array}\right]_{N * D_{\text {dim }}} \text {, } \end{aligned} $ | (1) |
其中:ubj和lbj是搜索区域边界;rand是(0, 1)内的随机数;X是由每个个体组成的矩阵;
因为每个鹈鹕的位置都对应一个方程的解,所以可以用公式(2)所示的目标函数推导出多个解,
| $ \boldsymbol{F i t}=\left[\begin{array}{c} F i t_1 \\ \vdots \\ F i t_i \\ \vdots \\ F i t_N \end{array}\right]_{N * 1}=\left[\begin{array}{c} F i t\left(X_1\right) \\ \vdots \\ F i t\left(X_i\right) \\ \vdots \\ F i t\left(X_N\right) \end{array}\right]_{N * 1} \text {, } $ | (2) |
其中:Fit是目标函数解的集合;Fiti是第i个鹈鹕所对应的函数值。
1.2 向猎物移动(探索阶段)探索阶段是在种群内随机选择特定的食物位置。另外,如果新的目标函数值更好,则接受新的鹈鹕位置。这降低了算法向非最优区域移动的概率。所用公式为
| $ x_{i, j}^{\mathrm{new}}= \begin{cases}x_{i, j}+{rand}\left(p_j-I * x_{i, j}\right), & F_p<F_i ,\\ x_{i, j}+{rand}\left(x_{i, j}-p_j\right), & \text { 其他 }, \end{cases} $ | (3) |
| $ X_i= \begin{cases}X_i^{\text {new }}, & F_i^{\text {new }}<F_i, \\ X_i, & \text { 其他 }, \end{cases} $ | (4) |
其中:xi, jnew表示第i个鹈鹕的第j维的新位置;I是1到2之间随机选择的数字;pj表示鹈鹕在第i次迭代时,第j维的位置;Fp为对应函数的值;Fi是当前第i只鹈鹕的适应度值;Finew是新产生的适应度值。公式(4)表示如果新的目标函数值更好,则接受新的鹈鹕位置以及其所对应的适应度值,否则不接受。
1.3 在水面上滑行(开发阶段)在开发阶段,一旦鹈鹕到达水面(确定搜索区域),它们会在水面上滑行,张大嘴巴,让更多的猎物进入口中(开发局部区域,以实现更充分的搜索)。这一阶段将提高局部搜索能力和挖掘能力。此外,还有一个接受新成员的进程。所用公式为
| $ x_{i, j}^{\mathrm{new}}=x_{i, j}+0.2\left(1-\frac{t}{T}\right) *(2 { rand }-1) x_{i, j} \text {, } $ | (5) |
| $ \vec{X}_i= \begin{cases}\vec{X}_i^{\text {new }}, & F_i^{\text {new }}<F_i, \\ \vec{X}_i, & \text { 其他 }, \end{cases} $ | (6) |
其中:xi, jnew表示第i个鹈鹕的第j维的新位置;t表示当前迭代次数;T表示最大迭代次数。
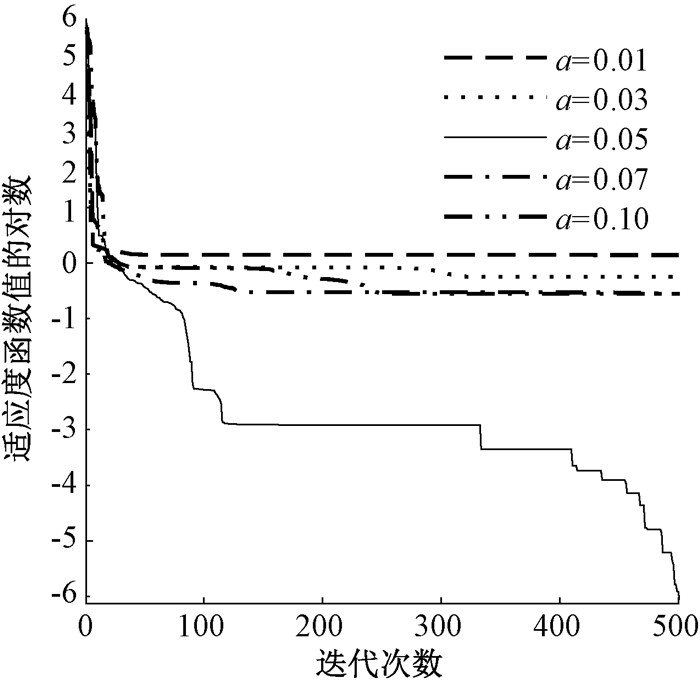
2 改进鹈鹕优化算法基础POA的开发阶段只搜索鹈鹕位置附近的点,然而,当面对多峰函数问题时,这种方法容易陷入局部最优。为了提高全局寻优能力,本文提出了一种随机扰动质量方法。首先,指定一个阈值,通过它来确定鹈鹕位置质量的高低,并计算每个个体的质量大小和干扰。对于质量较大的个体(质量大于指定的阈值),认为全局最优解的概率较高,因此,在它周围的一小块区域利用布朗运动来获取最优解信息,从而更加充分地发掘该位置的信息。对于质量较小的个体(质量小于指定的阈值),认为在它周围存在全局最优解的概率较低,因此,利用莱维飞行进行更大幅度的移动,从而使其跳出该区域,并发掘其他位置。通过此方法我们可以将低质量点转化为高质量点,从而增加算法跳出局部最优的概率。合理的阈值可以有效地过滤较差的个体,从而使算法具有更高效的性能。图 1显示了不同阈值的结果。我们发现,当阈值为0.05时,算法在收敛速度和收敛精度上都取得了较为满意的结果。所用公式为
|
图 1 不同阈值的收敛曲线 Fig. 1 Convergence curves of different thresholds |
| $ q_i=\frac{F_i-F_{\text {worst }}}{\sum\left(F_i-F_{\text {worst }}\right)} * \mathrm{e}^{F_{\text {rand }} / F_{\text {worst }}}, i=\{1, 2, \cdots, N\}, $ | (7) |
| $ { Brownian }={rand}\left(p i p, D_{\text {dim }}\right), $ | (8) |
| $ \begin{gathered} { Levy }=\lambda \times \frac{u}{|v|^{1 / \beta}} \lambda=0.01, \\ u={Normal}\left(0, \sigma_u^2\right), v={Normal}\left(0, \sigma_v^2\right), \\ \sigma_u=\left\{\frac{\Gamma(1+\beta) \cdot \sin (\pi \cdot \beta / 2)}{\beta \cdot \Gamma[(1+\beta) / 2] \cdot 2^{(\beta-1) / 2}}\right\}^{1 / \beta}, \sigma_v=1, \\ \Gamma(w)=\int_0^{\infty} t^{w-1} \mathrm{e}^{-t} \mathrm{~d} t, \end{gathered} $ | (9) |
| $ \begin{aligned} & X_{\_} {new }=X_i+ { Brownian } *\left(X_i- { Brownian } 1 * X_{\text {best }}\right), \\ & \text { 如果 } q \geqslant 0.05 *(1-t / T), \end{aligned} $ | (10) |
| $ X_{-} {new }=X_i+ { Levy } *\left(X_i-{Levy} 2 * X_{\text {best }}\right) \text {, } \\ 如果 q<0.05 *(1-t / T), $ | (11) |
其中:Fi为第i个总体适应度的值;Fworst表示总体适应度值的最差值;Frand表示随机的一个种群适应度值;qi是第i只鹈鹕位置信息的质量;Xbest表示适应度值最优所在的位置;X_new是经过质量扰动后产生的新解的位置;λ=β=0.01。
3 基于DPOA的图像匹配方法在进行图像匹配的过程中,其主要的框架由特征空间、搜索策略以及相似度量函数三部分组成。基于DPOA图像匹配的主要流程可以分为以下几个步骤:首先,在待匹配的图像中利用DPOA搜索目标图像;其次,利用特征描述方法将目标图像和待匹配图像表示出来,再利用相似度量函数得到图像相似程度,并且保留最相似的备选图像;最后,将完成迭代后得到的最大相似度值所对应的图像表示出来,也就是匹配的目标。
3.1 HOG特征提取方向梯度直方图(histogram of oriented gradients, HOG)是表示物体形状的局部强度梯度方向的一维直方图,该特征是局部区域相邻像素梯度的直方图,它不容易受到局部光照条件的影响,对几何形状的变化具有鲁棒性。因为在匹配过程中,图像的颜色对结果的影响不大,为了减小计算量并加快实验过程,对图像进行灰度化处理。计算每个像素点(x, y)的公式为
| $ G_{(x, y)}=\sqrt{G_x^2+G_y^2}, $ | (12) |
| $ \theta_{(x, y)}=\arctan \left(G_x / G_y\right), $ | (13) |
其中:G(x, y)和θ(x, y)是每个像素点的梯度幅值和梯度方向;Gx和Gy为像素点水平方向和垂直方向的梯度。
3.2 相似性度量相似性度量是为了将目标与模板之间的相似性可视化的一种手段,本文是将目标的HOG特征与模板的HOG特征通过相似度量函数将相似度表示出来。具体公式为
| $ \rho(X, Y)=\frac{{cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}, $ | (14) |
其中:X和Y分别是目标和模板的HOG特征;D(X)表示方差;cov(X, Y)为协方差;ρ(X, Y)为相关系数,其值越大,表示两张图像(模板和目标)的相似性越高,匹配的成功率也就越高,反之越小。
3.3 基于DPOA算法匹配流程将基于DPOA算法的图像匹配过程转化为寻优过程,每个个体均代表一个匹配结果,通过寻优过程将最优结果保存下来,直至满足迭代完成的条件。匹配步骤如算法1所示。
算法1 基于DPOA算法图像匹配流程
初始化:种群数量(备选图像位置)为n,当前迭代次数为t;最大迭代次数为T;保存最大相似值对应的坐标Xbest。
While t≤T
For i=1 to n //向猎物移动(探索阶段)
利用公式(3)更新每个个体的位置;
End
计算候选图像与目标图像之间的相似度,更新最优值Xbest位置;
For i=1 to n //在水面上滑行(开发阶段)
利用公式(5)更新每个个体的位置;
End
计算候选图像与目标图像之间的相似度,更新最优值Xbest位置;
For i=1 to n //质量扰动阶段
利用公式(7)计算个体的质量;
If Q(i) < 0.05*(1-t/T)
利用公式(10)更新个体;
Else
利用公式(11)更新个体;
End
计算候选图像与目标图像之间的相似度,更新最优值Xbest位置;
End
输出最佳位置Xbest。
4 仿真与结果分析本文所用实验环境为Windows 10系统,主要设备包括i7-11700 2.50 GHz CPU处理器;NVIDIA GeForce GTX 1050 Ti;采用Matlab R2019a语言实现。
4.1 测试及结果分析为了测试加入质量扰动后POA算法的性能,我们将算法在函数测试集CEC2019[15](共包含10个函数,本文选取其中七个)上进行测试,并与POA,DE,ALO,GOA和SSA五个算法进行比较,函数测试集共包含七个高度复杂的测试函数,每个函数都有自己的维度和搜索范围,如表 1所示。为了避免实验中发生意外,每个函数都单独运行50次,取值范围为(-100,100),种群数为30,最大迭代次数为500,之后保存数据的最优值(最小值)、平均值以及方差,并将最优数据加粗处理,比较结果如表 2所示。表中最优值表示算法运行50次所取得的最好结果,其值最小表示算法的寻优能力越强,平均值表示运行50次,将每次的最优值收集起来后取平均值,其值表示每次结果相对集中较多的中心位置,越小表示找到最优值的次数越多。方差表示数据的离散程度,越小表示算法的鲁棒性越高。
|
|
表 1 CEC2019测试函数库 Tab. 1 CEC2019 test function library |
|
|
表 2 六种算法在CEC2019测试函数集上优化结果对比 Tab. 2 Comparison of optimization results of six algorithms on the CEC2019 test function library |
由表 2可知,在大多数情况下,DPOA的性能要优于其他几种算法,其性能与POA相比,求解精度有所提高。从标准差可知,DPOA算法的鲁棒性也优于其他几种算法。此外,DPOA算法的运行时间为90.83 s,与原算法的69.22 s相比有所增加,但是寻优能力也得到了较大提升。与其他算法相比均取得了较好的运行结果,数据寻优能力也有所增加。
4.2 匹配实验及结果分析实验一 原始图像质量较好,没有噪声。
在烟叶生产过程中由于环境因素,实验车间总会掺杂一些飞虫等影响烟叶质量的东西。为了验证本文算法的可行性和有效性,将所提算法与原算法在烟虫图像匹配上进行对比实验。种群数量为N=50,最大迭代次数为T=100。实验结果如图 2和图 3所示。其中实线为DPOA算法的实验结果,虚线为POA算法的实验结果。

|
图 2 多只烟虫匹配实验对比图 Fig. 2 Comparison chart of multiple smoke bug matching experiments |

|
图 3 带有烟叶干扰匹配实验对比图 Fig. 3 Comparison chart of experiments with tobacco interference matching |
为了验证算法的鲁棒性,将两种方法的匹配实验分别进行50次,比较两种算法的平均匹配时间和正确匹配次数,实验结果与POA相比,DPOA在成功率上提升了8%,但匹配时间上升了1.77 s。虽然匹配时间有所增加,但是由于质量扰动方法的加入,使得算法跳出局部最优的概率增加,提高了寻优精度,即匹配成功的概率得到提升。
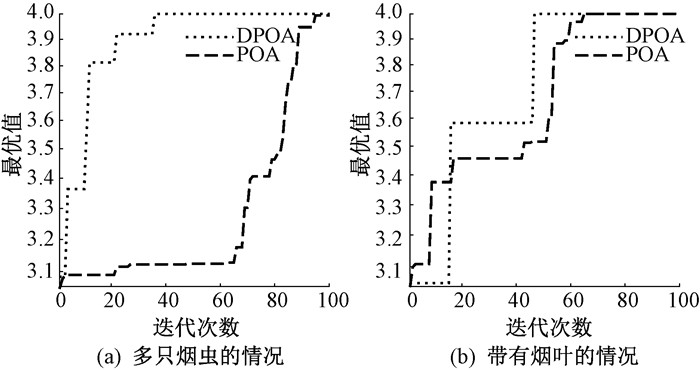
此外,为了更加直观地显示出DPOA算法在收敛速度以及收敛精度上的提升,将其迭代次数与平均适应度值的仿真结果进行比较,如图 4所示。
|
图 4 平均收敛曲线比较 Fig. 4 Comparison of average convergence curves |
从图 4给出的两种算法的平均收敛曲线可以看出,DPOA在处理复杂的实际问题时,无论从收敛速度和收敛精度上来说,均优于原算法,且跳出局部最优的能力得到增强。
实验二 原始图像质量较好,加入噪声。
为了测试基于DPOA算法的图像匹配方法的鲁棒性,我们对图像进行多种噪声干扰,由于噪声是一种不规则的错误,因而当图像加入噪声后,在捕捉、传输或处理过程中,会增加处理难度,也可检验算法的鲁棒性。图像加入噪声后结果如图 4所示。图 5(b)是加入均值为0、标准差为0.1的二维高斯分布噪声后的匹配结果,图 5(c)是加入泊松分布噪声后的匹配结果,图 5(d)是加入强度为0.02的椒盐噪声后的匹配结果。其中实线为DPOA算法的匹配结果,虚线为POA算法的匹配结果。将实验进行50次,比较两种算法的平均匹配时间以及正确率,结果如表 3所示。

|
图 5 加入噪声之后的匹配结果 Fig. 5 Matching results after adding noise |
|
|
表 3 加噪声后的实验数据 Tab. 3 Experimental data after adding noise |
从图 5可以看出,在加入噪声之后,DPOA算法仍然可以找到目标图像,其匹配效果也非常好,而原算法开始出现误差。50次实验中,两种算法在匹配时间上都有所增加,而DPOA的匹配时间虽然比原算法匹配时间久一些,但是在匹配结果上与原算法相比却有较大的优势。
5 结论本文针对传统图像匹配算法中存在调节参数多,效率低等问题,提出了一种基于质量扰动的鹈鹕优化算法,通过将匹配的过程转化为寻优过程,利用质量扰动可以较为充分地探索附近的点以及增加跳出局部最优的机会,弥补了原算法在解决多峰函数时容易陷入局部最优的缺陷。通过与多种算法在测试函数集CEC2019上进行对比实验,验证了DPOA方法的有效性和鲁棒性。与原算法进行的图像匹配实验证明了DPOA算法在处理实际问题时有较高的实际应用性。此外,我们提出的算法还将应用于图像增强和其他图像处理中,这将是未来的另一个关键问题。
| [1] |
MA J Y, JIANG X Y, FAN A X, et al. Image matching from handcrafted to deep features: a survey[J]. International journal of computer vision, 2021, 129(1): 23-79. DOI:10.1007/s11263-020-01359-2 (  0) 0) |
| [2] |
MA F. Explore the application of template matching technology in image recognition[J]. Electronic world, 2021(14): 138-139. (  0) 0) |
| [3] |
DOU J F, QIN Q, TU Z M. Robust image matching based on the information of SIFT[J]. Optik, 2018, 171: 850-861. DOI:10.1016/j.ijleo.2018.06.094 (  0) 0) |
| [4] |
MA L Y, SUN Y D, FENG N Z, et al. Image fast template matching algorithm based on projection and sequential similarity detecting[C]//2009 Fifth International Conference on Intelligent Information Hiding and Multimedia Signal Processing. Piscataway: IEEE Press, 2009: 957-960.
(  0) 0) |
| [5] |
DUAN H B, XU C F, LIU S Q, et al. Template matching using chaotic imperialist competitive algorithm[J]. Pattern recognition letters, 2010, 31(13): 1868-1875. DOI:10.1016/j.patrec.2009.12.005 (  0) 0) |
| [6] |
张焕龙, 郑卫东, 舒云星. 基于增量式互信息的图像快速匹配方法[J]. 弹箭与制导学报, 2015, 35(1): 135-138. ZHANG H L, ZHENG W D, SHU Y X. A new method of fast image matching based on incremental mutual information[J]. Journal of projectiles, rockets, missiles and guidance, 2015, 35(1): 135-138. (  0) 0) |
| [7] |
李强, 张钹. 一种基于图像灰度的快速匹配算法[J]. 软件学报, 2006, 17(2): 216-222. LI Q, ZHANG B. A fast matching algorithm based on image gray value[J]. Journal of software, 2006, 17(2): 216-222. (  0) 0) |
| [8] |
唐永鹤, 陶华敏, 卢焕章, 等. 一种基于Harris算子的快速图像匹配算法[J]. 武汉大学学报(信息科学版), 2012, 37(4): 406-409. TANG Y H, TAO H M, LU H Z, et al. A fast image matching algorithm based on Harris operator[J]. Geomatics and information science of Wuhan university, 2012, 37(4): 406-409. (  0) 0) |
| [9] |
周美茹. 细菌觅食优化算法研究及其在图像匹配中的应用[D]. 西安: 西安电子科技大学, 2014. ZHOU M R. Research on bacterial foraging optimization algorithm and its application in image matching[D]. Xi'an: Xidian University, 2014. (  0) 0) |
| [10] |
张焕龙, 张秀娇, 贺振东, 等. 基于布谷鸟搜索的图像匹配方法研究[J]. 郑州大学学报(理学版), 2017, 49(4): 51-56. ZHANG H L, ZHANG X J, HE Z D, et al. The study on image matching method based on cuckoo search[J]. Journal of Zhengzhou university (natural science edition), 2017, 49(4): 51-56. DOI:10.13705/j.issn.1671-6841.2017192 (  0) 0) |
| [11] |
王斐, 贾晓洪, 李丽娟, 等. 基于樽海鞘群算法的图像匹配方法[J]. 弹箭与制导学报, 2019, 39(5): 111-114. WANG F, JIA X H, LI L J, et al. Image matching based on salp swarm algorithm[J]. Journal of projectiles, rockets, missiles and guidance, 2019, 39(5): 111-114. (  0) 0) |
| [12] |
彭健, 曹中清. 基于DCT变换和鸡群优化算法的图像匹配[J]. 计算机与数字工程, 2020, 48(6): 1450-1455. PENG J, CAO Z Q. Image matching based on discrete cosine transform and chicken swarm optimization algorithm[J]. Computer & digital engineering, 2020, 48(6): 1450-1455. DOI:10.3969/j.issn.1672-9722.2020.06.035 (  0) 0) |
| [13] |
TROJOVSKY P, DEHGHANI M. Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications[J]. Sensors, 2022, 22(3): 855. (  0) 0) |
| [14] |
ANDERSON J G T. Foraging behavior of the American white pelican (pelecanus erythrorhyncos) in western Nevada[J]. Colonial waterbirds, 1991, 14(2): 166-172. (  0) 0) |
| [15] |
PRICE K V, AWAD N H, ALI M Z, et al. Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization[M]. Technical Report. Singapore: Nanyang Technological University, 2018.
(  0) 0) |
 2024, Vol. 56
2024, Vol. 56


