2. 郑州大学 力学与工程科学学院 河南 郑州 450001
2. School of Mechanics and Engineering Science, Zhengzhou University, Zhengzhou 450001, China
交通体系的发展在带来便利的同时,也因振动问题给周边环境带来不可忽略的影响.对此类振动进行研究和控制是交通实现可持续发展的关键问题之一[1].这种由不平顺激发的随机振动具有强烈的耦合和随机特性,对整体模型进行高效计算分析的研究尚不多见.文献[2]用车-桥-地基建立动力学模型,计算分析了车辆、轨道、桥梁、地面等部位的振动.文献[3]用数值方法计算了地下轨道交通引起的振动波在不同土层的传播特性.文献[4]通过汽车冲击振动试验和数值模拟方法,研究了振源特性与地面振动的传递函数关系.文献[5]采用数值和试验实测方法对交通引起的环境振动问题进行了系统的研究,建立了车辆-结构-周围环境-建筑物系统分析模型.文献[6]运用有限元数值方法,从车辆-轨道动力学理论角度讨论了临界速度附近土体的振动与衰减.文献[7]成功地将三维问题降为2.5维,解决了列车运动荷载作用下的三维动力问题.文献[8]采用解析法分析了铁路引起的环境振动问题,建立了基于虚拟激励法和车辆-轨道-路基-地基耦合系统垂向振动解析模型有效结合的算法.文献[9]通过大量的实测数据和数值分析总结了振动波的传播特性与规律.目前数值分析方面的研究面临以下三个难题:一是建立合理的分析模型;二是振动系统的计算效率与精度;三是复杂的随机特性描述.这些难题的攻克要以先进的随机振动计算方法为前提,虚拟激励法自20世纪80年代被提出来后,先后应用到工程领域诸多随机问题的数值分析实践中,取得了公认的成果[10].
本文研究了公路交通荷载耦合随机振动诱发的毗邻建筑二次振动响应.以垂向振动为主,采用Kelvin地基上的纵向无限长Kirchhoff板模拟路面及基础结构,通过位移协调条件与移动车辆构建耦合关系,建筑与基础结构采用线性阻尼器进行耦合,从而将环境振动的三个子系统耦合为统一的振动模型;考虑一个典型路面子结构模型,证明链式子结构的辛正交特性,基于辛数学方法[11]求解结构振动响应;基于虚拟激励法[12]建立车辆拟静止而支撑路面移动的二维移动单元格式求解,有效地提高了计算效率.用数值算例对车辆、支撑路面及毗邻建筑的随机响应进行了分析,得到一些有意义的结论.
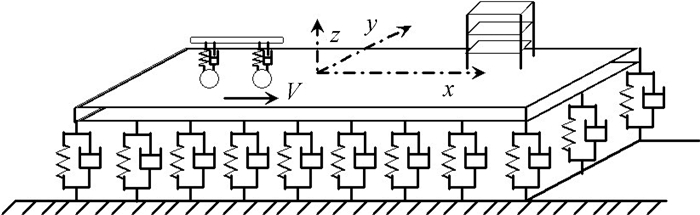
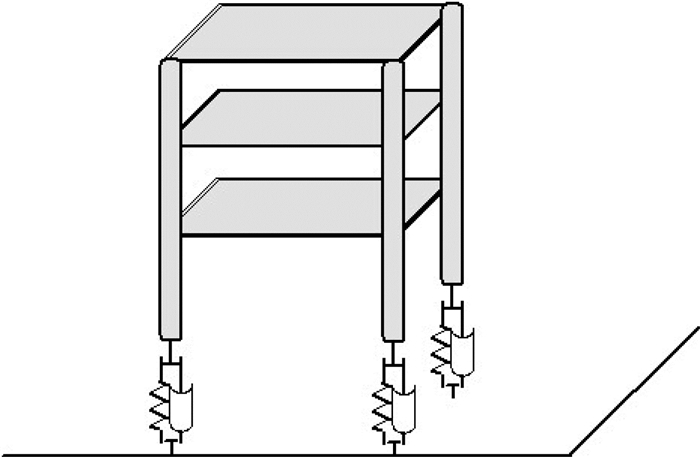
1 交通荷载模型及移动单元格式公路交通荷载耦合系统引起的邻近建筑振动力学模型如图 1所示.以Kelvin地基上的纵向无限长Kirchhoff板模拟路面支撑体系;车辆采用对称四自由度刚体模型,根据位移协调条件与支撑体系耦合;以三层梁柱模型模拟邻近受振建筑,以弹性连接与支撑结构耦合,建筑与基础结构耦合模型如图 2所示.对于车辆-路面耦合随机振动模型,车辆以弹簧、质量、阻尼组成的多刚体描述,路面以弹性半空间模拟,系统的运动微分方程表示为
|
图 1 交通荷载环境振动模型 Fig. 1 The model of traffic load environment vibration |
|
图 2 建筑与基础结构耦合模型 Fig. 2 The coupling model of building and foundation structure |
| $ D{\nabla ^2}{\nabla ^2}\mathit{\boldsymbol{u}} + \mu \mathit{\boldsymbol{u}} + \eta \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + m\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}} = \mathit{\boldsymbol{p}}\left( t \right)\delta \left( {x - Vt} \right), $ | (1) |
式中:u代表路面位移;抗弯刚度D=Eh3/12(1-υ),其中h、E、υ分别为路面模型的厚度、弹性模量和泊松比;m为路面质量密度;μ为地基反应模量;η为地基阻尼;p为车辆荷载;V为移动速度;∇2为拉氏算子.
本文采用移动单元法建立以速度V移动的相对坐标系.对路面进行有限元离散后,假定其为以速度V移动的单元,则在这个单元上车辆是静止的,属于平稳随机振动.离散后的路面移动单元如图 3所示.

|
图 3 离散后的路面移动单元 Fig. 3 The moving unit of the discretized pavement |
建立与荷载接触的四边形移动单元,给出相对坐标系参数为
| $ X = x - Vt;Y = y. $ | (2) |
在相对坐标系下,单元的动力学方程可以表示为
| $ D{\nabla ^2}{\nabla ^2}\mathit{\boldsymbol{u}} + \mu \mathit{\boldsymbol{u}} + \eta \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} - V\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial X}}} \right) + m\left( {\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}} - 2V\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial t\partial X}} + {V^2}\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {X^2}}}} \right) = \mathit{\boldsymbol{p}}\delta \left( X \right). $ | (3) |
对路面位移采用形函数离散,Kelvin地基上的Krichhoff板的形函数表示为
| $ {N_k} = \left( {1 + {\xi _0}} \right)\left( {1 + {\psi _0}} \right)\left( {2 + {\xi _0} + {\psi _0} - {\xi ^2} - {\psi ^2}} \right)/8, $ | (4) |
| $ {N_{{x_k}}} = - b{\psi _k}\left( {1 + {\xi _0}} \right)\left( {1 + {\psi _0}} \right)\left( {1 + {\psi ^2}} \right)/8, $ | (5) |
| $ {N_{{y_k}}} = - a{\xi _k}\left( {1 + {\xi _0}} \right)\left( {1 + {\psi _0}} \right)\left( {1 - {\xi ^2}} \right)/8. $ | (6) |
则位移向量可以表示为u=Nue.
移动荷载此时只与该单元接触,故对于式(3),其外力项除了移动荷载接触点外均为零,是一个0、1向量.采用弱积分形式可以获得离散的动力学振动方程,表示为
| $ \int {\int_s {\mathit{\boldsymbol{N}}\left[ {D{\nabla ^2}{\nabla ^2}\mathit{\boldsymbol{u}} + \mu \mathit{\boldsymbol{u}} + \eta \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} - V\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial X}}} \right)} \right]{\rm{d}}s} } + \\\int {\int_s {\mathit{\boldsymbol{N}}\left[ {m\left( {\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}} - 2V\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial t\partial X}} + {V^2}\frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {X^2}}}} \right) - \mathit{\boldsymbol{p}}\delta \left( X \right)} \right]{\rm{d}}s} } = 0, $ | (7) |
| $ \mathit{\boldsymbol{Ke}} = \int {\int_s {BDB{\rm{d}}s} } + \mu \int {\int_s {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}s} } - V\eta \int {\int_s {\frac{{\partial {\mathit{\boldsymbol{N}}^{\rm{T}}}}}{{\partial X}}\mathit{\boldsymbol{N}}{\rm{d}}s} } + m{V^2}\int {\int_s {\frac{{{\partial ^2}{\mathit{\boldsymbol{N}}^{\rm{T}}}}}{{\partial {X^2}}}\mathit{\boldsymbol{N}}{\rm{d}}s} } , $ | (8) |
| $ C\mathit{\boldsymbol{e}} = \eta \int {\int_s {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}s} } - 2Vm\int {\int_s {\frac{{\partial {\mathit{\boldsymbol{N}}^{\rm{T}}}}}{{\partial X}}\mathit{\boldsymbol{N}}{\rm{d}}s} } , $ | (9) |
| $ M\mathit{\boldsymbol{e}} = m\int {\int_s {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}s} } , $ | (10) |
| $ M\mathit{\boldsymbol{\ddot u}} + C\mathit{\boldsymbol{\dot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}, $ | (11) |
式中:u={u1,u2,…,un}为系统中各子系统结构的节点位移向量.从单元刚度矩阵和阻尼矩阵中可以看出,速度的影响被耦合进去,从而使得系统运动方程的右端荷载项不再随时间变化,是线性非时变的,故属于平稳随机振动,相对于非平稳问题,求解更简单.
2 移动单元法的虚拟激励形式对于耦合随机振动方程(11),根据传统的随机振动理论,有
| $ {\mathit{\boldsymbol{S}}_{{\rm{out}}}}\left( \omega \right) + {\mathit{\boldsymbol{H}}^ * }\left( \omega \right){\mathit{\boldsymbol{S}}_{{\rm{in}}}}\left( \omega \right){\mathit{\boldsymbol{H}}^{\rm{T}}}\left( \omega \right), $ | (12) |
式中:Sin(ω)代表输入激励;Sout(ω)代表输出响应;二者的变换由系统的频响函数矩阵H(ω)实现,*和T分别表示转置与共轭.基于虚拟激励法思想,路面不平顺激励可以用确定性的简谐激励表达.对于图 1问题,引入r(x)为路面不平顺量,可以表示为
| $ \mathit{\boldsymbol{r}}\left( x \right) = {\left\{ {r\left( x \right),r\left( {x - {l_t}} \right)} \right\}^{\rm{T}}}, $ | (13) |
式中:lt为前后悬架的间距.设r(x)的功率谱Sr(Ω)已知,当移动单元以车辆速度向后匀速运动时,根据坐标变换(2)式,功率谱可以表示为
| $ {\mathit{\boldsymbol{S}}_r}\left( \omega \right) = {\mathit{\boldsymbol{S}}_r}\left( \mathit{\Omega } \right)/V;\omega = \mathit{\Omega }V, $ | (14) |
式中:ω、Ω分别表示时域和空间域的圆频率.将不平顺激励代入移动单元格式的虚拟激励,有
| $ \mathit{\boldsymbol{\tilde r}}\left( t \right) = {\left\{ {{{\tilde r}_1},{{\tilde r}_2}} \right\}^{\rm{T}}} = {\left\{ {{{\rm{e}}^{ - {\rm{i}}\omega {t_1}}},{{\rm{e}}^{ - {\rm{i}}\omega {t_2}}}} \right\}^{\rm{T}}}\sqrt {{\mathit{\boldsymbol{S}}_r}\left( \omega \right)} {{\rm{e}}^{{\rm{i}}\omega t}}. $ | (15) |
式(15)代表一个简谐轨道不平顺激励.将
| $ {\mathit{\boldsymbol{S}}_{{\rm{in}}}}\left( \omega \right) = {{\mathit{\boldsymbol{\tilde r}}}^ * }{{\mathit{\boldsymbol{\tilde r}}}^{\rm{T}}};{\mathit{\boldsymbol{S}}_{{\rm{out}}}}\left( \omega \right) = {{\mathit{\boldsymbol{\tilde u}}}^ * }{{\mathit{\boldsymbol{\tilde u}}}^{\rm{T}}}. $ | (16) |
问题就转化为了求解简谐激励
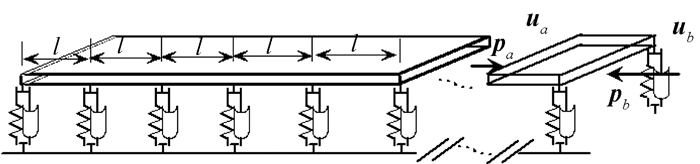
真实路面支撑结构是无限长延续的,若取大规模模型进行计算会导致计算困难,若取部分模型进行计算则会引起振动传递截断,带来误差,给数值分析造成精度问题.这里将路面支撑体系模型视为无限长周期性链式子结构,如图 4所示.
|
图 4 路面周期子结构模型 Fig. 4 The periodic model of pavement substructure |
取长度为l的路面结构作为一个子结构,考虑圆频率为ω的简谐波在路面结构中的传播.考虑系统的滞变阻尼,每一个子结构都有边界和内部节点,为了区分方便,取下标a表示左边界节点,b代表右边界节点,i代表内部节点,u和p代表位移和力向量.以矩形单元子结构为例,有12*12个自由度,运动方程中质量M和刚度矩阵K分别耦合路面结构u和车辆d的部分.通常不受外力作用的子结构可以内部消去,得
| $ \left( {{{\rm{e}}^{{\rm{i}}v}}\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_i}}\\ {{\mathit{\boldsymbol{u}}_a}}\\ {{\mathit{\boldsymbol{u}}_b}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{ii}^0}&{\mathit{\boldsymbol{K}}_{ia}^0}&{\mathit{\boldsymbol{K}}_{ib}^0}\\ {\mathit{\boldsymbol{K}}_{ai}^0}&{\mathit{\boldsymbol{K}}_{aa}^0}&{\mathit{\boldsymbol{K}}_{ab}^0}\\ {\mathit{\boldsymbol{K}}_{bi}^0}&{\mathit{\boldsymbol{K}}_{ba}^0}&{\mathit{\boldsymbol{K}}_{bb}^0} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_i}}\\ {{\mathit{\boldsymbol{u}}_a}}\\ {{\mathit{\boldsymbol{u}}_b}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_i}}\\ {{\mathit{\boldsymbol{p}}_a}}\\ {{\mathit{\boldsymbol{p}}_b}} \end{array}} \right\}. $ | (17) |
表示成状态空间向量的形式为
| $ {\mathit{\boldsymbol{S}}_H}\left( \omega \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{aa}}}&{{\mathit{\boldsymbol{S}}_{ab}}{{\rm{e}}^{ - {\rm{i}}v}}}\\ {{\mathit{\boldsymbol{S}}_{ba}}{{\rm{e}}^{{\rm{i}}v}}}&{{\mathit{\boldsymbol{S}}_{bb}}} \end{array}} \right]\left( {{y_b} = \mathit{\boldsymbol{S}}\left( \omega \right){y_a}} \right). $ | (18) |
可以验证
| $ {\mathit{\boldsymbol{S}}^{ - {\rm{T}}}} = \mathit{\boldsymbol{JS}}{\mathit{\boldsymbol{J}}^{ - 1}}\;或\;{\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{JS}} = \mathit{\boldsymbol{J}}, $ | (19) |
| $ \mathit{\boldsymbol{J}} = \left[ {0{\mathit{\boldsymbol{I}}_n}; - {\mathit{\boldsymbol{I}}_n}0} \right], $ | (20) |
式中:J是单位辛矩阵;In是n阶单位阵,说明矩阵S(ω)满足辛正交关系.假设S(ω)有2n个特征值,将其分成μ和1/μ两组,响应的特征向量构成如下矩阵:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {{\mathit{\boldsymbol{\varphi }}_1},{\mathit{\boldsymbol{\varphi }}_2}, \cdots ,{\mathit{\boldsymbol{\varphi }}_{2n}}} \right] \equiv \left[ {{\mathit{\boldsymbol{X}}_a}{\mathit{\boldsymbol{X}}_b};{\mathit{\boldsymbol{N}}_a}{\mathit{\boldsymbol{N}}_b}} \right]. $ | (21) |
则ua、ub、pa、pb和pi可以由特征向量表示为
| $ {\mathit{\boldsymbol{u}}_a} = {\mathit{\boldsymbol{X}}_b}\mathit{\boldsymbol{\lambda }};{\mathit{\boldsymbol{u}}_b} = {\mathit{\boldsymbol{X}}_a}\mathit{\boldsymbol{\gamma }};{\mathit{\boldsymbol{p}}_i} = {\mathit{\boldsymbol{p}}_{ie}};{\mathit{\boldsymbol{p}}_a} = {\mathit{\boldsymbol{p}}_{ae}} \\- {\mathit{\boldsymbol{p}}_b}{\mathit{\boldsymbol{u}}_a};{\mathit{\boldsymbol{p}}_b} = {\mathit{\boldsymbol{p}}_{be}} - {\mathit{\boldsymbol{p}}_a}{\mathit{\boldsymbol{u}}_b};{\mathit{\boldsymbol{p}}_a} = {\mathit{\boldsymbol{N}}_a}\mathit{\boldsymbol{X}}_a^{ - 1};{\mathit{\boldsymbol{p}}_b} = - {\mathit{\boldsymbol{N}}_b}\mathit{\boldsymbol{X}}_b^{ - 1}, $ | (22) |
式中:λ、γ为待定系数向量;pa、pb为边界出口刚度阵;边界间的响应简谐荷载向量为pae、pbe、pie.由此可以确定含有待定系数的子结构振动方程为
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{aa}^ * }&{\mathit{\boldsymbol{K}}_{ab}^ * }\\ {\mathit{\boldsymbol{K}}_{ba}^ * }&{\mathit{\boldsymbol{K}}_{bb}^ * } \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\lambda }}\\ \mathit{\boldsymbol{\gamma }} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{p}}_a^ * }\\ {\mathit{\boldsymbol{p}}_b^ * } \end{array}} \right\}. $ | (23) |
根据振动波子结构双向传播的特性,任一个端面响应可以根据确定的λ、γ求出,即
| $ {\mathit{\boldsymbol{u}}_{kr}} = {\mathit{\boldsymbol{X}}_a}{\mu ^k}\mathit{\boldsymbol{\gamma }};{\mathit{\boldsymbol{p}}_{kr}} = {\mathit{\boldsymbol{p}}_a}{\mathit{\boldsymbol{u}}_{kr}}, $ | (24) |
式中:k的正、负表示外力左、右侧的端面.对于图 1问题,双轴与路面接触,选取接触位置的两个子结构单元
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{aa}^ * }&{\mathit{\boldsymbol{K}}_{ab}^ * }\\ {\mathit{\boldsymbol{K}}_{ba}^ * }&{\mathit{\boldsymbol{K}}_{bb}^ * } \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\lambda }}_i}}\\ {{\mathit{\boldsymbol{\gamma }}_i}} \end{array}} \right\} = \mathit{\boldsymbol{K}}_t^d\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\lambda }}_i}}\\ {{\mathit{\boldsymbol{\gamma }}_i}} \end{array}} \right\} = - \mathit{\boldsymbol{N}}\left( {{\xi _i}} \right){f_i},i = 1,2, $ | (25) |
式中:ξi为轮子接触点与子结构左侧距离;λi、γi代表第i个子结构的位移向量,由式(23)可以求得第i个子结构两端的位移为ul, i和ur, i,它由两个车轮接触力单独作用时的响应叠加而成,即
| $ {\mathit{\boldsymbol{u}}_{l,i}} = \sum\limits_{j = 1}^2 {{\mathit{\boldsymbol{u}}_{l,ji}}} ;{\mathit{\boldsymbol{u}}_{r,i}} = \sum\limits_{j = 1}^2 {{\mathit{\boldsymbol{u}}_{r,ji}}} . $ | (26) |
合并成一个方程,可得
| $ \mathit{\boldsymbol{\tilde K}}\tilde y = \mathit{\boldsymbol{\tilde F}};\mathit{\boldsymbol{\tilde K}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde K}}}_{vv}}}&{{{\mathit{\boldsymbol{\tilde K}}}_{vt}};}&{{{\mathit{\boldsymbol{\tilde K}}}_{tv}}}&{{{\mathit{\boldsymbol{\tilde K}}}_{tt}}} \end{array}} \right]. $ | (27) |
式(27)即为结构的动力学方程,
考虑如图 1所示的交通荷载环境振动模型,其中四自由度车辆模型参数为:mc=708 kg,mr=mf=80 kg,J=1 060 kg·m2,kr=19 326 N/m,kf=20 292 N/m,cr=cf=1 000 N·s/m,lt=1.308 m,f=1.168 m,wkr=wkf=128 760 N/m.公路模型参数为:E=1.516×1010 Pa,υ=0.35,ρ=7.66×102 kg/m2,h=0.15 m,μ=9.5×107 N/m3,路面板宽度为20 m,截取有效子结构长度l=0.8 m.采用国标GB—7031路面谱的形式Sr(ω)=2πGqn02(V/ω2),n0为参考空间频率,通常n0=0.1 m-1;公路级别通常分为8个等级,这里取C级路面谱值Gq=2.56×10-4 m3.假定车辆沿着x轴方向行驶,受振毗邻建筑为三层板式结构,层高3 m,楼板厚度0.15 m,柱横截面面积Ap=0.8 m2,混凝土密度为2.5×103 kg/m3,弹性模量为2.5×1010 N/m,采用Rayleigh阻尼,建筑接触竖向刚度为1.0×109 N/m,阻尼为3.475×106 N·s/m.
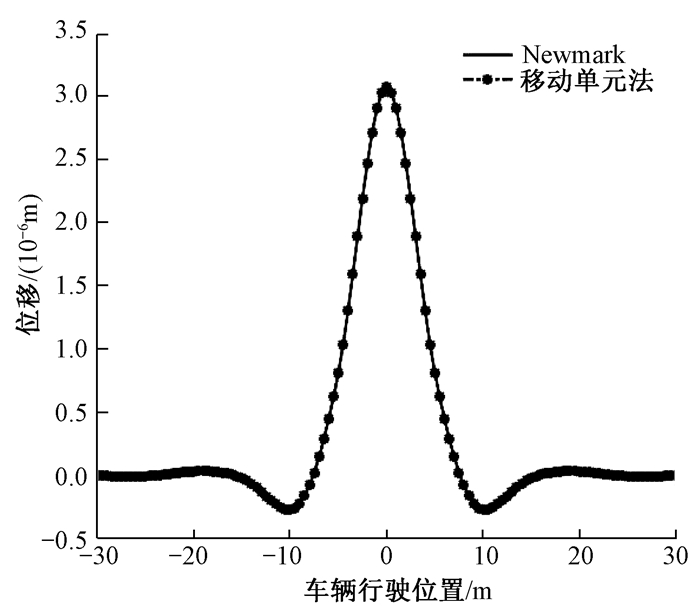
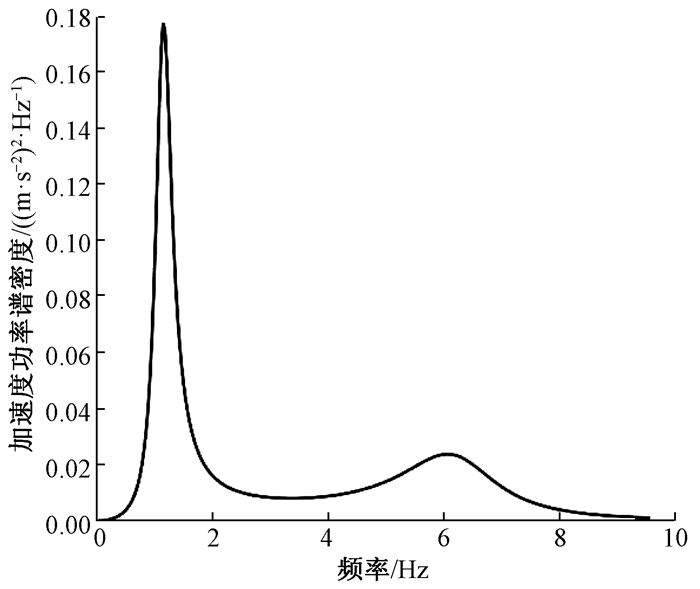
图 5为路面中轴位移响应, 给出了图 1模型使用本文移动单元法与经典Newmark-β算法的验证结果,可以看出两种算法结果吻合良好.图 6为公路路面地基板三维挠度响应.可以看出,当车辆运行时,对路面产生带状变形影响,路面板变形方向以沿车辆行进方向为主,按行车道中轴线横向扩展;由于邻近建筑的存在,使得路面板一侧刚度较大,沿刚度较大一侧变形褶皱要强于另一侧.图 7给出了行驶车辆受路面不平顺激励产生的竖向加速度功率谱密度响应.可以发现,车辆在运行过程中分别出现两个振动峰值1.3 Hz和6 Hz,这是因为前后轮间随机激励间的相位差,也即行波效应.
|
图 5 路面中轴位移响应 Fig. 5 The deflection response of pavement axis line |

|
图 6 地基板三维挠度响应 Fig. 6 The 3D deflection response of the foundation plate |
|
图 7 车辆竖向加速度功率谱密度响应 Fig. 7 The vertical acceleration power spectral density response of vehicle |
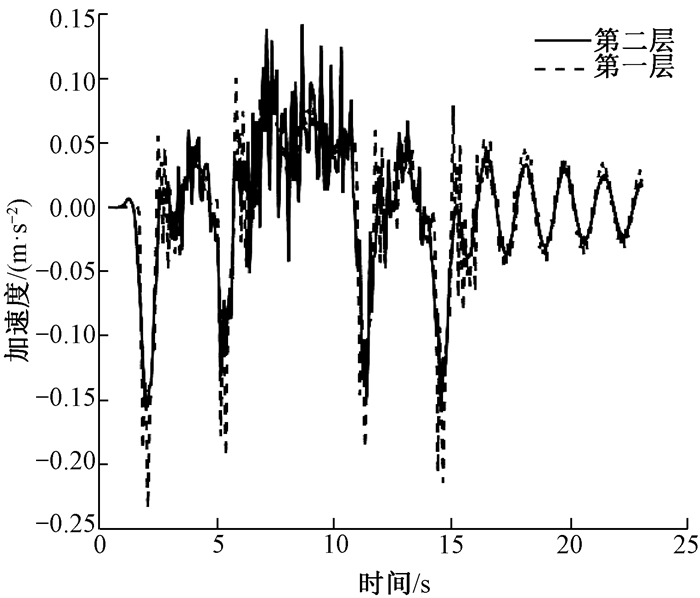
图 8为建筑结构中点加速度响应,给出了建筑受交通荷载的影响.结果表明,毗邻建筑受交通荷载的影响随车辆行驶从远到近而逐渐加剧,振源距离对建筑的影响为主要作用;且由于低楼层具有较大刚度,其加速度响应明显高于高楼层.随着荷载由近场驶向远场,振动响应趋于衰减,楼层之间的加速度响应差异不再明显,这是因为振动波在建筑体内迟滞传递的效果.
|
图 8 建筑结构中点加速度响应 Fig. 8 Mid-point acceleration response of building structures |
图 9为建筑结构加速度功率谱密度响应,计算了受振建筑各个楼层的加速度功率谱响应的频域特性及变化规律.结果表明,毗邻建筑垂向加速度功率谱密度在20 Hz左右达到峰值,加速度功率谱密度随楼层的升高而降低,但频域特征保持一致.同时也计算了不同楼层受振的位移均值响应,可以发现,建筑结构位移响应随车辆的驶近而加剧,其峰值与加速度随车辆位置的响应保持一致,且随着楼层的升高,位移响应变化增大,这与加速度功率谱密度值的变化规律相反.

|
图 9 建筑结构加速度功率谱密度响应 Fig. 9 The acceleration power spectral density response of building structure |
建立了振源子结构-传播路径-受振建筑一体的交通荷载诱发环境振动数值分析模型,采用链式子结构的周期性特性,用辛数学方法建立子结构的动态响应求解途径,基于虚拟激励法推导了移动荷载耦合随机振动的二维移动单元格式.通过计算分析得到以下结论:①通过周期性链式子结构的证明和应用,说明对无限长路面或轨道结构通过建立合理的子结构链,可以有效地避免人工边界条件的引入,减少数值计算产生的人为误差.②对非平稳多点耦合随机激励系统,移动单元格式使复杂的时变随机分析转化为非时变问题分析.③交通荷载引起的毗邻建筑结构的响应随车辆近场、远场关系影响明显,其幅值变化较大,尤其在高频部分,建筑体不同楼层之间的加速度和位移响应变化规律不同步;建筑结构的存在对路面动力响应影响不是很大.此外,由于本文的模型构建和推导存在一些假设,且缺乏实际测量数据和模型算例计算数据,因此其结果还需进行与实测结果的验证.
| [1] |
夏禾. 交通环境振动工程[M]. 北京: 科学出版社, 2010.
(  0) 0) |
| [2] |
HAYAKAWA K. Ground vibrations isolation by PC wall-piles[C]//Proceeding of 4th International Conference on Case Histories in Geotechnical Engineering. Saint Louis, 1998: 662-667.
(  0) 0) |
| [3] |
KURZWEIL L G. Ground-borne noise and vibration from underground rail systems[J]. Journal of sound and vibration, 1979, 66(3): 173-182. (  0) 0) |
| [4] |
DEGRANDE G, LOMBAERT G. High-speed train induced free field vibration: in situ measurements and numerical modelling[C]//Proceeding of the International Workshop on Wave Propagation, Moving Load and Vibration Reduction. Rotterdam, 2000: 29-41.
(  0) 0) |
| [5] |
曹艳梅, 夏禾, 王昆鹏, 等. 紧邻既有铁路桥基础施工对行车影响的预评估[J]. 铁道学报, 2013, 35(3): 95-101. DOI:10.3969/j.issn.1001-8360.2013.03.015 (  0) 0) |
| [6] |
翟婉明. 车辆-轨道耦合动力学[M]. 北京: 中国铁道出版社, 1997.
(  0) 0) |
| [7] |
蒋红光, 边学成, 徐翔, 等. 列车移动荷载下高速铁路板式轨道路基动力性态的全比尺物理模型试验[J]. 岩土工程学报, 2014, 36(2): 334-362. (  0) 0) |
| [8] |
冯青松, 雷晓燕, 练松良. 解析法分析铁路环境振动的列车随机激振荷载[J]. 华东交通大学学报, 2013, 30(5): 1-7. DOI:10.3969/j.issn.1005-0523.2013.05.001 (  0) 0) |
| [9] |
崔高航, 陶夏新, 陈宪麦. 轨道交通引起地面环境振动最小二乘法分析[J]. 哈尔滨工业大学学报, 2008, 40(8): 1184-1188. DOI:10.3321/j.issn:0367-6234.2008.08.002 (  0) 0) |
| [10] |
林家浩, 张亚辉, 赵岩. 虚拟激励法在国内外工程界的应用回顾与展望[J]. 应用数学和力学, 2017, 38(1): 1-31. (  0) 0) |
| [11] |
钟万勰. 应用力学对偶体系[M]. 北京: 科学出版社, 2002.
(  0) 0) |
| [12] |
林家浩, 张亚辉. 随机振动的虚拟激励法[M]. 北京: 科学出版社, 2004.
(  0) 0) |
 2019, Vol. 51
2019, Vol. 51


