2. 中国科学院 软件研究所 计算机科学国家重点实验室 北京 100190;
3. 珠海澳大科技研究院 广东 珠海 519000
2. State Key Laboratory of Computer Science, Institute of Software, Chinese Academy of Science, Beijing 100190, China;
3. Zhuhai-UM Science and Technology Research Institute, Zhuhai 519000, China
在计算机图形学领域, 基于物理的可变形物体的模拟与仿真始终是人们研究的热点之一.其应用范围主要包括虚拟手术[1-2], 计算机动画[3-4], 以及通过模拟来指导工程模型的建造等[5-6].近年在Siggraph、Eurographics、SCA等国际著名图形学会议上多有关于此类问题的研究报道[7-11].
基于物理的可变形物体的模拟与仿真从材料的本质属性出发, 能够更加真实、准确地模拟物体的变形过程, 但同时需要求解复杂的运动方程, 所以既要保证模拟的计算效率, 又要提高模拟的真实度与灵活性一直是个挑战性问题.随着近年来计算机硬件的飞速发展和计算能力的不断增强, 基于物理的变形模拟效率已得到有效提高, 研究者们不断开发模拟更为复杂的混合材料, 以提供丰富的视觉效果, 满足人们对真实感及灵活性的需求.此前, 基于物理的变形模型综述[7], 主要对常见的模型离散方法, 如有限元法、有限差分法、质量弹簧法等, 进行了分类和总结, 并结合相应采用的时间积分算法进行了讨论, 指出了热门的应用方向.黄绍辉等[8]对采用有限元模型仿真可变形物体的相关研究进行了综述, 将典型的有限元模拟方法进行了分类比对.石敏等[9]对布料动画方法的研究进行了综述, 根据生成动画所采用的技术不同, 将其分为几何法、物理法等7个大类进行对比分析. Frerichs等[10]针对由自然环境所引起的物体形态变化, 如金属表面的腐蚀、植物的枯萎腐败等现象, 概述了此类变形模拟方法的研究现状. Wu Jun等[11]讨论了基于物理的可变形物体的切割模拟方法, 主要针对切割引起的拓扑结构变化等问题, 及相应解决方案进行了分类探讨.在基于物理的变形模拟方法中, 材料的本构模型决定了其响应变形的物理特性, 因此本文主要针对近十年基于物理的变形模拟中所采用的本构模型进行分析和概括, 并根据模拟材料的不同进行分类和展开, 最后进行讨论总结.
1 基本的本构模型Terzopoulos等人[12-13]首先将基于物理的变形模拟应用到了图形学领域中, 近年来得到了广泛的研究与发展.其中本构模型是材料物理特性的数学表达, 描述了材料响应变形的方式, 如应力变化、能量变化, 可以通过应力P关于变形梯度F的函数P(F), 或能量密度Ψ关于F的函数Ψ(F)来表达[14].应变张量E用来表示变形的程度, 也可以由变形梯度推导出.目前比较流行的关于应变张量的两种选择分别是Green应变张量EG和Cauchy应变张量EC.所用公式为EG(F)=(FTF-I)/2, EC(F)=(FT+F)/2-I, 其中Green应变张量是非线性的, 具有旋转不变性, 因此基于该应变的弹性模型模拟结果更加准确, 但求解方式较为复杂和耗时.将Green应变张量用泰勒公式展开, 可以得到线性的Cauchy应变张量, 基于线性应变的模型求解方式简单, 计算效率高, 是早期基于物理的变形模拟最常用的方法.其能量密度方程为Ψ(F)=μ||EC||F2+(λtr2(EC))/2, 其中μ、λ为拉梅系数, 由杨氏模量和泊松比构成.线性Cauchy应变只适用于小变形的模拟, 它能够有效模拟物体的伸缩变形, 却不能正确模拟物体的旋转.事实上旋转操作不会引起物体的变形以及能量密度的变化, 但在柯西应变中, 旋转会导致物体体积的变化从而产生大量误差, 如图 1(a)所示, 模型头部由于受力旋转而导致体积变大.

|
图 1 线性Cauchy模型与corotated模型对比 Figure 1 Comparison between linear Cauchy model and corotated model |
为了解决上述问题, Müller[15-16]提出了同步旋转(corotated)线弹性模型, 仅通过对应变添加旋转矩阵来保持变形的旋转不变性, 求解复杂度比非线性Green应变模型降低很多, 随后得到了广泛应用, 其修正结果如图 1 (b)所示.该方法对变形梯度进行极分解F=RS, 即将其分为旋转和缩放两部分, 其能量密度函数为
| $ \mathit{\Psi }\left( \mathit{\boldsymbol{F}} \right) = \mu \left\| {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{R}}} \right\|_F^2 + \left( {\lambda {\rm{t}}{{\rm{r}}^2}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{I}}} \right)} \right)/2. $ |
采用Green非线性应变的弹性模型称为St.Venant-Kirchhoff模型, 它能够保证物体的旋转不变性, 较好地模拟大变形.但是非线性模型会导致求解复杂度的提高和时间消耗的增大, 因此出现了一些针对此类模型加速方法的研究[17-18].
上述如Cauchy线性应变一类的线性量度称之为几何线性, 而如Hookean材料中应力与应变的线性依赖关系称之为材料线性.材料线性的物体在变形过程中, 应力随着变形的增大而增强, 但到达一定阈值时, 应力反而会减小, 从而在极端压缩的情况下, 变形物体的体积被压缩至0, 甚至出现倒转, 从而产生不稳定的模拟结果.为解决此类问题, 研究者们采用应力-应变关系为非线性的本构模型, 如采用Neo-Hookean模型来进行模拟.
除了线性与非线性的本构模型特征, 材料属性还存在各向同性与各向异性之分.各向同性材料如橡胶、金属, 其在各个方向上具有相同的物理特性; 各向异性材料如人类的肌肉组织、树木等, 其在物体本身特定的轴向上具有更强的应变能力.下面本文根据材料的不同特性, 对近十年来基于物理的变形模拟研究进行分类, 具体分为超弹性材料、黏弹性材料、弹塑性材料和各向异性材料, 并结合其各自采用的本构模型进行详细探讨.
2 本构模型在不同材料中的应用 2.1 超弹性材料对于许多材料, 弹性模型只能近似模拟其变形过程, 而不能准确表达.例如橡胶, 其应力-应变关系实则为非弹性的, 此时需要采用超弹性模型进行建模求解.而超弹性材料在极大变形情况下, 其模拟方法的鲁棒性是一个挑战性问题.
部分文章[19-21]在corotated线性本构模型的基础上, 采用6面体网格的FEM数值离散化方法, 模拟了超弹性材料行为.其中McAdams等人[22]通过观察发现, 在corotated能量密度方程中, 主要由μ||F-R||F2决定模拟的稳定性, 而(λtr2(RTF-I))/2对稳定性的影响几乎可以忽略不计.因此该方法对μ项进行调整, 将其拆分为1个采用更复杂、稳定的方式进行求积的Laplace能量密度Ψ△, 以及1个采用简单的1点求积方式的辅助能量密度Ψaux, 从而改善了大变形行为中的不稳定现象, 并尽量控制了开销, 其能量密度函数为
| $ \mathit{\Psi } = \underbrace {\mu \left\| \mathit{\boldsymbol{F}} \right\|_F^2}_{{\mathit{\Psi }_\Delta }}\underbrace { - 2\mu {\rm{tr}}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{F}}} \right) + \mu \left\| \mathit{\boldsymbol{I}} \right\|_F^2 + \frac{\lambda }{2}{\rm{t}}{{\rm{r}}^2}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{I}}} \right)}_{{\mathit{\Psi }_{aux}}} $ |
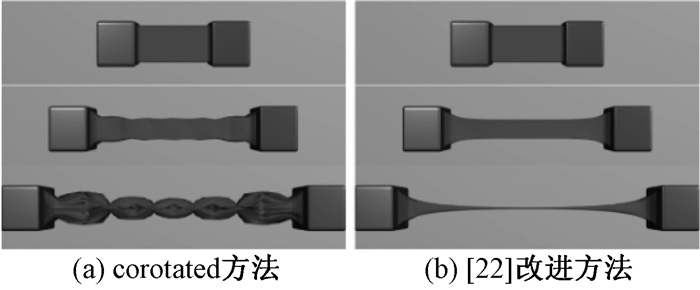
图 2(b)展示了该方法与图 2(a)corotated方法相比, 模拟极大变形的结果更加稳定.
|
图 2 超弹性模型的极大变形模拟 Figure 2 Large deformation of hyperelastic model |
Fedkiw等人[21-22]提出了倒转有限元(invertible finite element, IFE)方法, 对1st Piola-Kirchoff应力进行求解.通过对变形梯度进行奇异值分解, 即
| $ \mathit{\Psi } = \frac{\mu }{2}\left( {{\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^{\rm{T}}}\mathit{\boldsymbol{\hat F}}} \right) - 3} \right) - \mu \ln \left( J \right) + \frac{\lambda }{2}{\ln ^2}\left( J \right), $ |
其中

|
图 3 不同方法模拟极大变形的结果 Figure 3 Large deformation simulation with different methods |
黏弹性材料通常用于对复杂流体进行模拟, 黏性指流体内部阻碍其自由流动的力.如Dariusz[25]所述, 通常用于模拟流体的Navier-Stokes方程的黏性系数设置为常量, 不足以描述这样复杂的材料行为, 因而需要在方程中添加更为复杂的本构模型进行模拟.弹塑性材料多指固体, 如钢材, 在经历小变形时展现出线弹性行为, 而当变形程度超过一个临界值时, 呈现出塑性行为, 即物体无法恢复原形.对此两类材料的模拟有着相似之处, 可将变形梯度分为弹性和塑性两部分, 即F=FEFP.
Ram等人[26]采用了包含本构模型的动态方程来模拟黏弹性液体的运动.对于塑性变形部分, 通常有Von Mises[27]和Oldroyed-B[28]两种模型, 前者的数值离散方法更为复杂, 所以该文选择后者进行模拟, 并通过定义一个新的左Cauchy-Green应变使得该塑性变形模拟可以保持物体的体积.弹性部分则采用了可压缩的Neo-Hookean弹性能量密度模型,
| $ \mathit{\Psi }\left( {{\mathit{\boldsymbol{b}}^\mathit{\boldsymbol{E}}}} \right) = \frac{\mu }{2}\left( {{\rm{t}}r\left( {{\mathit{\boldsymbol{b}}^\mathit{\boldsymbol{E}}}} \right) - 3} \right) - \mu \ln \left( J \right) + \frac{\lambda }{2}{\left( {J - 1} \right)^2}, $ |
其中bE=FEFET, 为左Cauchy-Green应变. 图 4展示了该方法模拟黏性流体的结果.

|
图 4 奶油派扔向人体模型的模拟结果 Figure 4 A pie with a stiff crust and soft whipped cream is thrown at a mannequin |
Stomakhin等人[29]首次将物质点方法(material point method, MPM)应用到图形学领域, 对雪进行了模拟.雪具有可压缩性, 并且受温度、湿度等环境因素的影响, 而呈现出固、液以及混合的多态性.为实现这种复杂的多态材料模拟, 该方法在塑性变形部分采用基于主拉伸的屈服准则, 提高了用户对参数设置的可控性.同时仅通过修改能量密度中的拉梅参数来简化材料的硬化行为.文章采用了Cauchy应力, 其能量密度函数定义为
| $ \mathit{\Psi }\left( {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{E}}}, {\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{P}}}} \right) = \mu \left( {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{P}}}} \right)\left\| {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{E}}} - {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{E}}}} \right\|_F^2 + \frac{{\lambda \left( {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{P}}}} \right)}}{2}{\left( {{\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{E}}} - 1} \right)^2}, $ |
其中弹性部分采用了corotated线弹性模型, 拉梅参数则通过塑性变形梯度设置为
| $ \mu \left( {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{P}}}} \right) = {\mu _0}{{\rm{e}}^{\xi \left( {1 - {\mathit{\boldsymbol{J}}_P}} \right)}}, \lambda \left( {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{P}}}} \right) = {\lambda _0}{{\rm{e}}^{\xi \left( {1 - {J_P}} \right)}}, $ |
其中:JE=det(FE); JP=det(FP); λ0、μ0为初始拉梅系数; ξ为塑料硬化参数.同时定义了压缩临界值θC和拉伸临界值θS来控制启用塑性变形, 即FE的奇异值在[1-θC; 1+θS]范围内.当物体进行小变形时, 由弹性变形梯度FE控制; 当变形程度超出临界值时, 开始产生塑性变形.
Klar等人[30]对Mast等人[31-32]模拟弹塑性颗粒材料的方法进行了改进, 模拟了沙堆的变形.文章将Drucker-Prager塑性流动模型与基于Hencky应变的超弹性模型相结合.该方法相较于文献[29]的方法, 物理精确度更高.通过奇异值分解F=UΣVT, 定义应变张量为

|
图 5 模拟结果与真实情况的对比 Figure 5 Comparison between the simulation and the ground truth |
Tampubolon等人[34]在文献[30]的基础上进行了多孔隙沙堆与水混合的材料变形模拟.相较于干沙堆, 湿沙堆可以通过张力保持自己的形态, 这一现象利用在模型中添加凝聚力来实现, 凝聚力的大小随混合材料中水的饱和程度而变化, 其对应的屈服条件为
| $ {C_F}{\rm{tr}}\left( {{\mathit{\boldsymbol{\sigma }}^s}} \right) + {\left\| {{\mathit{\boldsymbol{\sigma }}^s} - \frac{{{\rm{tr}}\left( {{\mathit{\boldsymbol{\sigma }}^s}} \right)}}{3}I} \right\|_F} \le {C_C}, $ |
其中:σs为沙粒部分的应力; CC≥0为对凝聚力的约束, 随着材料中凝聚量的增多而增大; CF≥0为对摩擦力的约束, 随沙粒间产生摩擦的量而增长.例如在文献[30]的方法中, CC设置为0, 而本文中的凝聚力由混合材料中水的容积率ϕw=ρw/ρ决定, 有CC=CC(φw).该方法对于弹性应变部分, 在文献[30]本构模型的基础上, 乘以一个分段函数

|
图 6 不同凝聚力的沙堆通过楔形物坠落的模拟结果 Figure 6 Dropping sand on wedges with various cohesion values |
前面所述的各种材料的变形模拟都是基于各向同性的, 生活中还有许多各向异性材料, 如人类的肌肉, 树木等.各向异性材料已被广泛讨论[35], 多数被应用于医学领域人体器官、软组织等的变形模拟及布料模拟. Liao等人[36]利用医学CT数据生成了横向各向同性和正交各向异性的骨骼材料. Talbot等人[37]使用横向各向同性材料构建了电子心脏模型.文献[38]通过对Cauchy应变张量中的每个元素单独进行约束, 来模拟各向异性的双向纺织材料.Wang等人[39]提出了一种分段的线性各向异性布料模型.
各向同性材料无论是在物质坐标系下, 还是在空间坐标系下都具有旋转不变性, 而各向异性材料则不具备物质坐标系的旋转不变性. Irving等人[21]对变形梯度进行奇异值分解
前面所述的这些方法大多研究的是横截各向异性材料, 即在三维坐标空间中, 有两个方向的刚度相等. Li等人[40]提供了一种通用的线性各向异性材料的变形模拟, 可以在3个正交方向上, 设置3种不同的刚度参数, 同时在保证稳定性的前提下, 向用户提供了1种直观的方式来调节这些参数.该方法采用了corotated的线弹性本构模型, 由于应变张量ε与应力张量σ的对称性, 可将其展开成为6×1的向量, 即ε=[ε11ε22ε332ε122ε232ε31]T, σ=[σ11σ22σ33σ12σ23σ31]T, 下标11, 22, 33对应了正向应力应变, 12, 23, 31对应了切向应力应变. 6×6的弹性张量E用来描述应力-应变关系, 有σ=Eε, E可以简写为
| $ \mathit{\boldsymbol{E}} = \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ 0&\mathit{\boldsymbol{B}} \end{array}} \right]. $ |
对于各向同性材料, 有
| $ \mathit{\boldsymbol{A}} = \frac{\kappa }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[{\begin{array}{*{20}{c}} {1-\nu }&\nu &v\\ \nu &{1-\nu }&\nu \\ \nu &\nu &{1-\nu } \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B = }}\frac{\kappa }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[{\begin{array}{*{20}{c}} {1-2\nu }&0&0\\ 0&{1-2\nu }&0\\ 0&0&{1-2\nu } \end{array}} \right], $ |
其中:κ为杨氏模量; ν为泊松比.它们共同决定了材料的应力-应变属性.而该方法提出的通用线性各向异性材料, 为不同方向上的应变设置了不同的属性, 则上式A和B可以重新定义为
| $ \mathit{\boldsymbol{A}} = \gamma \left[{\begin{array}{*{20}{c}} {{\kappa _1}\left( {1-{\nu _{23}}{\nu _{32}}} \right)}&{{\kappa _2}\left( {{\nu _{12}} + {\nu _{32}}{\nu _{13}}} \right)}&{{\kappa _3}\left( {{\nu _{13}} + {\nu _{12}}{\nu _{23}}} \right)}\\ {{\kappa _1}\left( {{\nu _{21}} + {\nu _{31}}{\nu _{23}}} \right)}&{{\kappa _2}\left( {1-{\nu _{13}}{\nu _{31}}} \right)}&{{\kappa _3}\left( {{\nu _{23}} + {\nu _{21}}{\nu _{13}}} \right)}\\ {{\kappa _1}\left( {{\nu _{31}} + {\nu _{21}}{\nu _{32}}} \right)}&{{\kappa _2}\left( {{\nu _{32}} + {\nu _{12}}{\nu _{31}}} \right)}&{{\kappa _3}\left( {1-{\nu _{12}}{\nu _{21}}} \right)} \end{array}} \right],\\ \mathit{\boldsymbol{B}} = \left[{\begin{array}{*{20}{c}} {{\mu _{12}}}&0&0\\ 0&{{\mu _{23}}}&0\\ 0&0&{{\mu _{31}}} \end{array}} \right], $ |
其中:γ=1/(1-ν12ν21-ν23ν32-ν13ν31-2ν21ν32ν13);
|
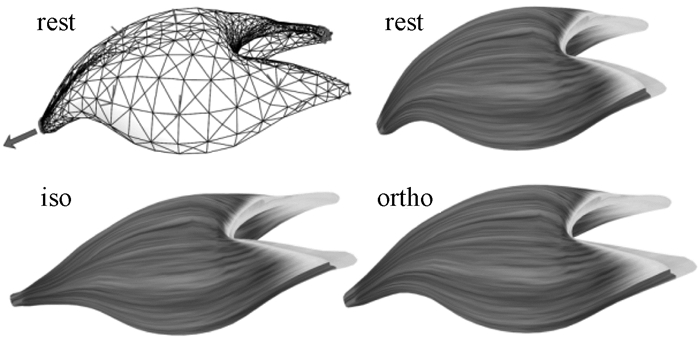
图 7 各向同性材料与正交各向异性材料变形对比 Figure 7 Isotropic material deformation compared with orthotropic material deformation |
表 1将本节所述文献所采用的本构模型以及相应的模型离散方法进行了归纳.
|
|
表 1 本构模型以及模型离散方法归类 Table 1 Classification of constitutive models and discretization methods |
从本构模型在基于物理的变形模拟中的发展来看, 近年来的研究热点主要有3个方面:1)解决模型在极度变形时所产生的走样问题, 如极度拉伸情况下产生的抖动, 以及极度压缩情况下产生的单元体倒转, 此类问题所研究的材料属于超弹性材料, 只包含1个本构模型, 多采用FEM方法对模型进行离散处理, 如文献[19-24]. 2)模拟混合材料或多相材料的变形动画, 如雪从固态到液态变形的不同结果, 沙子与水的融合交互, 此类材料多为弹塑性或黏弹性材料, 可包含多个不同特性的本构模型, 多采用MPM的模型离散方法, 能够更加灵活地处理不同状态下本构模型的差异, 如文献[26]和[29-34].这种对于混合及多相材料的模拟正逐步将固体变形与流体动画同化融合, 因此选择能够适应不同本构模型的模型离散以及数值求解方法, 以保证模拟的真实感和计算效率, 本文认为有可能成为未来此类问题的重点研究思路. 3)各向异性材料的模拟, 如文献[21]和[36-40], 首先现实生活中有很多材料如肌肉组织、植物组织等都具有各向异性, 因此实现材料的各向异性可以增强模拟的真实感.其次在电影、动画、游戏等领域, 设计者们也可以通过自己天马行空的想象, 创造出丰富的虚拟材料, 来向观众呈现出更加生动有趣的虚拟世界, 对材料各向异性的模拟无疑为此提供了便利.
4 总结本文对基于物理的变形模拟研究进展进行了综述, 主要对其所采用的物理材料及相关本构模型进行了分类概括, 结合模型离散和数值求解方法, 我们可以归纳出此类基于物理的变形模拟的研究思路:即通过开发或改进新型的本构模型, 来模拟复杂材料的变形过程, 以追求更加丰富灵活的视觉效果; 再根据材料特性, 选择合适的模型离散方法和数值求解方法进行求解, 以提高模拟的时间效率.随着计算机硬件的发展和计算能力的提升, 使复杂的非线性材料模拟性能得到了提升, 因此对于混合材料和多相材料的模拟成为了研究热点.未来还可以将模型分割与材料各向异性模拟进行结合, 创造出新型材料, 从而进一步丰富变形模拟的动画.同时, 提高模拟效率, 增强实时交互也将一直是该领域的研究热点.
| [1] |
WU W, HENG P A. An improved scheme of an interactive finite element model for 3D soft-tissue cutting and deformation[J]. The visual computer, 2005, 21(8): 707-716. (  0) 0) |
| [2] |
LIU Y Q, JIAO S H, WU W, et al. GPU accelerated fast FEM deformation simulation[C]//IEEE Asia Pacific Conference on Circuits and Systems, APCCAS 2008. Macao, 2008: 606-609.
(  0) 0) |
| [3] |
CHANG Y Z, BAO K, LIU Y Q, et al. A particle-based method for viscoelastic fluids animation[C]//Proceedings of the ACM Symposium on Virtual Reality Software and Technology. Kyoto, 2009: 111-117.
(  0) 0) |
| [4] |
XU H Y, BARBIČ J. Pose-space subspace dynamics[J]. ACM transactions on graphics, 2016, 35(4): 1-14. (  0) 0) |
| [5] |
BICKEL B, BÄCHER M, MIGUEL A, et al. Design and fabrication of materials with desired deformation behavior[J]. ACM transactions on graphics, 2010, 29(4): 1-10. (  0) 0) |
| [6] |
CHEN D, LEVIN D I W, Matusik W, et al. Dynamics-aware numerical coarsening for fabrication design[J]. ACM transactions on graphics, 2017, 36(4): 1-15. (  0) 0) |
| [7] |
NEALEN A, MÜLLER M, KEISER R, et al. Physically based deformable models in computer graphics[J]. Computer graphics forum, 2006, 25(4): 809-836. (  0) 0) |
| [8] |
黄绍辉, 王博亮. 使用有限元模型仿真可变形物体的研究进展[J]. 系统仿真学报, 2007, 19(22): 5315-5320. DOI:10.3969/j.issn.1004-731X.2007.22.051 (  0) 0) |
| [9] |
石敏, 毛天露, 夏时洪, 等. 布料动画方法研究进展及问题[J]. 计算机学报, 2012, 35(12): 2446-2458. (  0) 0) |
| [10] |
FRERICHS D, VIDLER A, GATZIDIS C. A survey on object deformation and decomposition in computer graphics[J]. Computers and graphics, 2015, 52: 18-32. DOI:10.1016/j.cag.2015.06.004 (  0) 0) |
| [11] |
WU J, WESTERMANN R, DICK C. A survey of physically based simulation of cuts in deformable bodies[J]. Computer graphics forum, 2015, 34(6): 161-187. DOI:10.1111/cgf.12528 (  0) 0) |
| [12] |
TERZOPOULOS D, PLATT J, BARR A, et al. Elastically deformable models[J]. ACM siggraph computer graphics, 1987, 21(4): 205-214. DOI:10.1145/37402 (  0) 0) |
| [13] |
TERZOPOULOS D, FLEISCHER K. Modeling inelastic deformation: viscolelasticity, plasticity, fracture[J]. ACM siggraph computer graphics, 1988, 22(4): 269-278. DOI:10.1145/378456 (  0) 0) |
| [14] |
SIFAKIS E, BARBIČ J. FEM simulation of 3D deformable solids: a practitioner′s guide to theory, discretization and model reduction[C]//ACM SIGGRAPH Courses. California, 2012: 1-35.
(  0) 0) |
| [15] |
MÜLLER M, DORSEY J, MCMILLAN L, et al. Stable real-time deformations[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. San Antonio, 2002: 49-54.
(  0) 0) |
| [16] |
MÜLLER M, GROSS M. Interactive virtual materials[C]//Proceedings of Graphics Interface. London, 2004: 239-246.
(  0) 0) |
| [17] |
BARBIČ J, JAMES D J. Real-time subspace integration for St. Venant-Kirchhoff deformable models[J]. ACM transactions on graphics, 2005, 24(3): 982-990. DOI:10.1145/1073204 (  0) 0) |
| [18] |
HUANG J, SHI X H, LIU X G, et al. Subspace gradient domain mesh deformation[J]. ACM transactions on graphics, 2006, 25(3): 1126-1134. DOI:10.1145/1141911 (  0) 0) |
| [19] |
CHAO I, PINKALL U, SANAN P, et al. A simple geometric model for elastic deformations[J]. ACM transactions on graphics, 2010, 29(4): 38. (  0) 0) |
| [20] |
MCADAMS A, ZHU Y N, SELLE A, et al. Efficient elasticity for character skinning with contact and collisions[J]. ACM transactions on graphics, 2011, 30(4): 37. (  0) 0) |
| [21] |
IRVING G, TERAN J, FEDKIW R. Invertible finite elements for robust simulation of large deformation[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Grenoble, 2004: 131-140.
(  0) 0) |
| [22] |
TERAN J, SIFAKIS E, IRVING G, et al. Robust quasistatic finite elements and flesh simulation[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Los Angeles, 2005: 181-190.
(  0) 0) |
| [23] |
STOMAKHIN A, HOWES R, SCHROEDER C, et al. Energetically consistent invertible elasticity[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Lausanne, 2012: 25-32.
(  0) 0) |
| [24] |
LIU T T, BOUAZIZ S, KAVAN L. Quasi-Newton methods for real-time simulation of hyperelastic materials[J]. ACM transactions on graphics, 2017, 36(3): 23. (  0) 0) |
| [25] |
NIEDZIELA D. On numerical simulations of viscoelastic fluids[D]. Kaiserslautern: Technische University of Kaiserslautern, 2006.
(  0) 0) |
| [26] |
RAM D, GAST T, JIANG C F F, et al. A material point method for viscoelastic fluids, foams and sponges[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Los Angeles, 2015: 157-163.
(  0) 0) |
| [27] |
YUE Y H, SMITH B, BATTY C, et al. Continuum foam: a material point method for shear-dependent flows[J]. ACM transactions on graphics, 2015, 34(5): 160. (  0) 0) |
| [28] |
TERAN J, FAUCI L, SHELLEY M. Peristaltic pumping and irreversibility of a Stokesian viscoelastic fluid[J]. Physics of fluids, 2008, 20(7): 73-101. (  0) 0) |
| [29] |
STOMAKHIN A, SCHROEDER C, CHAI L, et al. A material point method for snow simulation[J]. ACM transactions on graphics, 2013, 32(4): 102. (  0) 0) |
| [30] |
KLAR G, GAST T, PRADHANA A, et al. Drucker-prager elastoplasticity for sand animation[J]. ACM transactions on graphics, 2016, 35(4): 103. (  0) 0) |
| [31] |
MAST C M. Modeling landslide-induced flow interactions with structures using the material point method[D]. Seattle: University of Washington, 2013.
(  0) 0) |
| [32] |
MAST C M, ARDUINO P, MACKENZIE-HELNWEIN P, et al. Simulating granular column collapse using the material point method[J]. Acta geotechnica, 2015, 10(1): 101-116. DOI:10.1007/s11440-014-0309-0 (  0) 0) |
| [33] |
KLAR G, GAST T, PRADHANA A, et al. Drucker-prager elastoplasticity for sand animation[J]. ACM transactions on graphics, 2016, 35(4): 103. (  0) 0) |
| [34] |
TAMPUBOLON A P, GAST T, KLÁR G, et al. Multi-species simulation of porous sand and water mixtures[J]. ACM transactions on graphics, 2017, 36(4): 105. (  0) 0) |
| [35] |
BOWER A F. Applied mechanics of solids[M]. Boca Raton: CRC press, 2009.
(  0) 0) |
| [36] |
LIAO S H, TONG R F, DONG J X. Anisotropic finite element modeling for patient-specific mandible[J]. Computer methods and programs in biomedicine, 2007, 88(3): 197-209. DOI:10.1016/j.cmpb.2007.09.009 (  0) 0) |
| [37] |
TALBOT H, MARCHESSEAU S, DURIEZ C, et al. Towards an interactive electromechanical model of the heart[J]. Interface focus, 2013, 3(2): 20120091. DOI:10.1098/rsfs.2012.0091 (  0) 0) |
| [38] |
THOMASZEWSKI B, PABST S, STRABER W. Continuum-based strain limiting[J]. Computer graphics forum, 2009, 28(2): 569-576. (  0) 0) |
| [39] |
WANG H M, O′BRIEN J F, RAMAMOORTHI R. Data-driven elastic models for cloth: modeling and measurement[J]. ACM transactions on graphics, 2011, 30(4): 71. (  0) 0) |
| [40] |
LI Y J, BARBIĈ J. Stable anisotropic materials[J]. IEEE transactions on visualization and computer graphics, 2015, 21(10): 1129-1137. DOI:10.1109/TVCG.2015.2448105 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


