郑州大学学报（理学版）  2017, Vol. 49 Issue (1): 103-107  DOI: 10.13705/j.issn.1671-6841.2016230

引用本文  

刘莹, 张建华, 师会谭, 等. 基于线性神经网络和多参数的蛋白质相似度算法[J]. 郑州大学学报(理学版), 2017, 49(1): 103-107.
LIU Ying, ZHANG Jianhua, SHI Huitan, et al. Protein Similarity Algorithm Based on a Linear Neural Network and Multiparameter[J]. Journal of Zhengzhou University(Natural Science Edition), 2017, 49(1): 103-107.

基金项目

国家自然科学基金项目(813D3150)

通信作者

张建华(1971—)，男，河北唐山人，副教授，主要从事医学工程技术与数据挖掘研究，E-mail:petermails@163.com

作者简介

刘莹(1989—)，女，河南南阳人，硕士研究生，主要从事多参数信息学研究，E-mail:1063251753@qq.com

文章历史

收稿日期：2016-09-13
Contents              Abstract              Full text              Figures/Tables              PDF
基于线性神经网络和多参数的蛋白质相似度算法
刘莹1 , 张建华1,2 , 师会谭1 , 张琳婧1     
1. 郑州大学 电气工程学院 河南 郑州450001;
2. 郑州大学 医学工程技术与数据挖掘研究所 河南 郑州450001
收稿日期：2016-09-13
基金项目：国家自然科学基金项目(813D3150)
作者简介：刘莹(1989—)，女，河南南阳人，硕士研究生，主要从事多参数信息学研究，E-mail:1063251753@qq.com.
通信作者：张建华(1971—)，男，河北唐山人，副教授，主要从事医学工程技术与数据挖掘研究，E-mail:petermails@163.com.
摘要：提出一种新的蛋白质结构相似度算法，目的在于通过比对蛋白质的结构寻找功能上的相似性.收集约1 000对蛋白质的PDB结构文件，采用RCSB PDB结构比对工具获取每一对蛋白的结构匹配相似度，并计算每一对蛋白质的9个参数的相似度.采用线性神经网络建立总体相似度和9个参数之间的数学模型.计算模型的仿真误差，并选取若干蛋白质对该算法模型进行应用验证.所建立模型仿真误差为8.76%，验证结果与已有工具结果基本相同，但个别有一定差异.该算法可用于比较蛋白质的结构相似度，且比对结果可以对蛋白质功能的相似性进行提示.
关键词：蛋白质    相似度    多参数    算法模型    线性神经网络    
Protein Similarity Algorithm Based on a Linear Neural Network and Multiparameter
LIU Ying1 , ZHANG Jianhua1,2 , SHI Huitan1 , ZHANG Linjing1     
1. School of Electrical Engineering of Zhengzhou University, Zhengzhou 450001, China;
2. Biomedical Engineering Technology and Data Mining Research Institution of Zhengzhou University, Zhengzhou 450001, China
Abstract: The study aimed to presented a new algorithm of proteins structure similarity.The aims of the algorithm was to find the similarity of function by proteins structure alignment.The data of more than 1 000 pairs of proteins were collected.Their similarities were obtained through RCSB PDB structure alignment tool, meanwhile, the similarity of nine parameters of every pairs of proteins were calculated. A linear neural network was adopted to establish the mathematical model between them and the simulation error of it was calculated.Several pairs protein were selected to verify the practicability.The mean error of the model is 8.76%. The result of the practicability verification was basically the same with existing tools except individual had some difference.The algorithm model can be used to evaluate the similarity of proteins structure and the result could signal the function similarity of proteins.
Key words: proteins    similarity    multiple parameter    algorithm model    linear neural network    
0 引言

生物学上一般采用BLAST(basic local alignment search tool)工具来获取蛋白质氨基酸序列的相似度[1].随着相关研究工作的进展，大量学者设计开发了其他序列匹配算法以改进BLAST算法的不足[2].然而，氨基酸序列的相似性只能提示两个蛋白是否具有足够的同源性，并不能满足学者对于功能表达相似性的研究.因此，现有研究中已出现了许多关于蛋白质结构相似度比对的工具.CE(combinatorial extension)和FATCAT(flexible structure alignment by chaining AFPs (aligned fragment pairs) with twists)算法是较早开始应用的蛋白质结构比对方法[3]，其中CE是采用增量式组合扩展的方法逐段比较对齐的两个蛋白结构片段，最后将其组合起来评价蛋白质相似度.FATCAT算法是CE算法的进一步改进.DALI是L Holm等设计开发的蛋白质对结构相似度在线工具，其主要计算方法是计算一对蛋白中原子的均方根误差(root-mean-square deviation, RMSD)，但用户在使用时需要上传处理过的PDB文件(该方法只能计算ATOM/HETATM部分).文献[4]结合TM得分旋转矩阵和动态调整方法设计出TM-align算法，该算法的计算速度大约是DALI和SAL方法的20倍，CE算法的4倍.鉴于各算法的不同，比对结果往往也不一致.RCSB PDB比对工具是RCSB PDB(RCSB protein data bank)数据库自主开发的一种用于匹配蛋白质结构相似度的Java web start应用程序，操作简便，可以实时在线精确匹配PDB数据库中的蛋白质结构文件，应用相对较为广泛.

现有蛋白质相似度比较方法中，基本都是从蛋白质三级结构出发，将其比对结果应用于蛋白质功能的相似性评价上.本文拟从多参数的角度评价蛋白质的相似度，建立相似度和各参数之间的数学关系模型，并依此对蛋白质功能的相似性进行提示.并采用该算法计算并筛选出与新发现的胃癌蛋白p42.3相似的蛋白，成功找出了p42.3的功能调控路径，从而证明了该算法的可用性.

1 材料和方法 1.1 数据收集 1.1.1 总体相似度和参数选择

从PDB(http://www.rcsb.org/pdb/home/home.do)数据库中先行收集相似蛋白质共1 005对，进而下载其结构数据PDB文件.然后通过RCSB PDB结构比对工具(http://www.rcsb.org/pdb/workbench/workbench.do?action=menu)获取每一对蛋白质的结构相似度作为标准相似度.在PDB文件中，只取ATOM及HETATM部分的数据进行9个参数相似度的计算，分别为空间密度、原子个数、氨基酸个数、氨基酸种类、C元素比例、N元素比例、O元素比例、P元素位置、S元素位置[5-6]，并分别标记为S1~S9.参数的选择标准均以与蛋白质功能表达相关为出发点.

1.1.2 密度相似度(S1)

首先在蛋白质内部以该蛋白中心原子为原点建立空间坐标系，将其余原子的坐标按统一位移向量变化.然后，计算每一个原子距原点的距离，根据距离将蛋白质划分为一层层的球壳.统计每一层球壳的原子数目，并比较两个蛋白在每一层的原子个数相似度，而后加权求和.当层数取得无穷大时，每一层球壳的厚度便无穷小，此时所计算的参数便可视为蛋白质的密度相似度.假设将蛋白质平均划分为n层，每一层相似度计算公式simi，每一层的相似度权值计算公式wi，n1i为其中为第一个蛋白第i层的原子个数，n2i为第二个蛋白第i层的原子个数，n1为第一蛋白质的原子总数，n2为另一个蛋白质的原子总数.

$ si{m_i} = 1-\frac{{\left| {{n_{1i}}-{n_{2i}}} \right|}}{{\left| {{n_{1i}} + {n_{2i}}} \right|}}, i = 1, 2, \ldots, n, \;\;{w_i} = (\frac{{{n_{1i}}}}{{{n_1}}} + \frac{{{n_{2i}}}}{{{n_2}}})/2, i = 1, 2, \ldots, n. $

因此，两个蛋白质的密度相似度可以表示为$S1 = \mathop {\lim }\limits_{n-\infty } \sum\limits_{i = 1}^n {si{m_i}{w_i}} .$.

1.1.3 原子数目、氨基酸数目及氨基酸种类相似度(S2、S3、S4)

每一个蛋白分子所包含的原子数目决定了分子的大小和质量，而氨基酸的数目和种类影响着蛋白质的功能.

$ S2 = 1-\frac{{\left| {{n_1}-{n_2}} \right|}}{{\left| {{n_1} + {n_2}} \right|}};S3 = 1-\frac{{\left| {{m_1} - {m_2}} \right|}}{{\left| {{m_1} + {m_2}} \right|}};S4 = 1 - \frac{{\left| {{k_1} - {k_2}} \right|}}{{\left| {{k_1} + {k_2}} \right|}}, $ (1)

其中:n1、m1、k1分别为第一个蛋白质的原子总数、氨基酸数目和氨基酸种类；n2、m2、k2分别为第二个蛋白质的原子总数、氨基酸数目和氨基酸种类.

1.1.4 C、N、O元素比例相似度(S5、S6、S7)

S5~S7计算方法相同，均按照公式(2) 进行计算，其中:ne1是第一个蛋白质中的C/N/O元素个数; ne2是第二个蛋白质中的C/N/O元素个数; n1和n2分别为两个蛋白质的原子总数.

$ S = 1-\frac{{\left| {\frac{{{n_{e1}}}}{{{n_1}}}-\frac{{{n_{e2}}}}{{{n_2}}}} \right|}}{{\left| {\frac{{{n_{e1}}}}{{{n_1}}} + \frac{{{n_{e2}}}}{{{n_2}}}} \right|}}. $ (2)
1.1.5 P和S元素的相似度(S8、S9)

P和S元素在蛋白质中的含量相对较偏少，但其对蛋白质作用的发挥起着关键的作用，因此，P、S元素的相似度也是评价两个同源蛋白相似度的一个重要因素.其中，S8为P元素位置相似度，计算定义为:若两个蛋白均不含P元素，则该相似度为1；若其中一个含有而另一个不含有，则相似度为0.如果两个蛋白质均含有P元素，查找P元素位置和其距原点原子的距离，并按照距离获取其所在的层数(S1计算过程中的分层)，如果两个蛋白所含P原子位于相同层，则相似度为1；在相邻层，则相似度为0.5，除此之外的情况则相似度为0.S9为S元素的位置相似度，计算方法同P元素.

因此，按照上述方法可以计算出每一对蛋白的9个参数的相似度，将其与总相似度S一起组成样本数据用于之后的建模分析.所收集部分数据如表 1所示.

表 1 所收集数据S及S1~S9的均值和标准差 Table 1 Mean and standard deviation of S1~S9 and collected data S
1.2 线性神经网络模型的建立

神经网络为采用单层感知器结构时，所建立模型可视为线性模型[7].作为一种线性分类器，单层感知器尽管结构简单，却能够学习并解决相当复杂的问题.假设S和S1~S9之间的关系是线性的，因此单层感知器可以对其建模一个方程.神经网络学习的过程就是一个权值调节过程，最终会输出一个权值矩阵[8].在本方法中，随机选取所有数据集中80%的数据用于对模型进行训练，将其余的20%数据用于对模型验证，所设置训练误差阈值为0.001，最大训练次数为5 000，输入层节点数为9，输出层节点数为1，因此，训练结束后会得到一个1*9的系数向量w和一个常数项B.此时，相似度S按$S = \sum\limits_{{\rm{i}} = 1}^{\rm{k}} {{w_i}{s_i}} + B, i = 1, 2, \cdots, 9$来计算.

选取数据集中剩余的20%的数据对模型进行误差验证.将数据按照相似度S的公式进行计算，并与已知结果进行比较，误差计算方法$ME = \frac{1}{n}\sum {\left| {S-{S_o}} \right|/S} $，其中:ME为平均误差；So为所建立模型的计算输出；S为已知输出.

2 结果

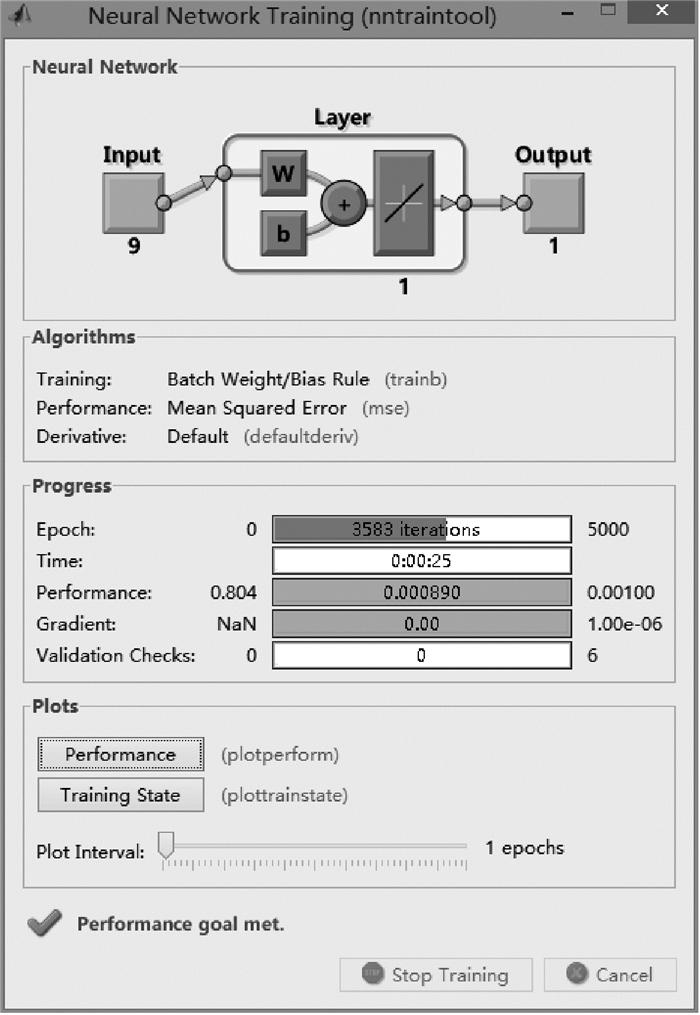
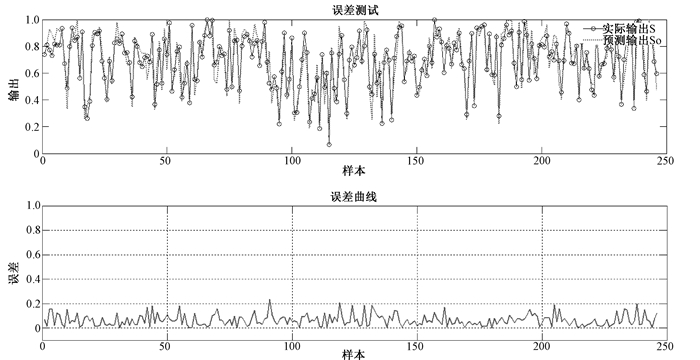
所建立神经网络为单层感知器线性神经网络，训练过程如图 1所示.该训练过程结束后，输出各参数系数如表 2所示.由此可得，所建立的数学模型为:S=0.319 8S1+0.034 3S2+0.027 9S3+0.061 8S4+0.065 3S5+0.106 2S6+0.103 2S7+0.147 7S8+0.148 0S9-0.014 2.仿真误差如图 2所示，平均误差ME计算结果为8.67%.分别用该算法模型和RCSB PDB比对工具及BLAST进行相似度的计算，并比较其结果如表 3所示.

图 1 训练过程 Figure 1 Training process

表 2 各参数系数 Table 2 Coefficient of every parameter

图 2 误差曲线 Figure 2 Error curve

表 3 所用模型与已有工具比较 Table 3 Comparison between models and existing tools
3 讨论

本文提出一种新的基于多参数和线性神经网络的蛋白质相似度算法，建立了蛋白质相似度和其9个参数之间的数学模型.该算法是从分析蛋白质结构相似度出发，旨在对蛋白质功能的相似性进行提示，所选用参数也均与蛋白质功能的表达相关.

已有一些学者的研究证明，多参数评价蛋白质相似度较单一参数更为合适[9-10, 13]，文献[11]通过比较两个蛋白的骨架碳原子曲线参数比较蛋白质的相似度，例如曲率、扭力和翻转变体等.文献[12]通过对氨基酸以及蛋白质多肽链中的特殊结构的分析，综合考虑了蛋白质结构中骨架碳原子数、突变原子数、亲水微粒数和螺旋数4个参数，并依托模糊数学等价矩阵理论，提出一种新的相似度算法，证明其性能比考虑单一参数更好.神经网络是近代应用逐渐广泛的人工智能算法[14]，并且对神经网络采用单层感知器即可建立线性模型，在数据量较大时，对数据进行特征提取后，再利用神经网络进行分类会节省时间.因此，本文所采用的简单线性神经网络模型，对其进行的误差分析及结果验证都表明了其良好的性能.从表 3可以看出，本算法的计算结果同RCSB PDB比对工具的结果基本相同，但个别具有一定差异.如1AAX(酪氨酸激酶)和101M(抹香鲸肌红蛋白)的相似度，3B94(人GITRL蛋白)和4DB5(家兔GITRL蛋白)的相似度相比较，RCSB PDB结构比对工具的结果较高，而3WD5(人TNFα与阿达木抗体结合蛋白)和2TNF(小鼠TNFα蛋白)的相似度相对其较低.具体分析可知，1AAX和101M以及3B94和4DB5均含有S元素且所在位置非常接近，而S元素在蛋白质中的作用一般是形成二硫键，以此来影响蛋白质高级结构的生物活性和蛋白质的复性等功能特点[15].而3WD5和2TNF虽然也含有S元素，但其所在位置较为不同(一个在蛋白分子表面, 而另一个在内部靠近中心位置), 另外，BLAST同源性也表明了二者的相似程度.

采用本文的算法，可以初步计算并筛选出与p42.3具有相同结构域且总体相似度在80%以上的蛋白质集，推测出p42.3的生物学功能和调控路径与这些蛋白相似.在后期进行的Weston Blot及PCR生物学实验结果验证了这一预测.本文中所采用的9个参数主要提取自蛋白质的空间结构PDB文件，在参数的选择和计算方法方面尚需要进一步改进.随着研究的深入和样本量的增多，算法将会得到进一步的优化.

参考文献
[1]
JOHNSON M, ZARETSKAYA I, RAYTSELIS Y, et al. NCBI blast: a better web interface[J]. Nucleic acids research, 2008, 36(S2): 5-9. (0)
[2]
YE Y, CHOI J H, TANG H. RAP rearch: a fast protein similarity search tool for short reads[J]. BMC bioinformatics, 2011, 12(1): 159. DOI:10.1186/1471-2105-12-159 (0)
[3]
SHINDYALOV I N, BOURNE P E. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path[J]. Protein engineering, 1998, 11(9): 739-747. DOI:10.1093/protein/11.9.739 (0)
[4]
ZHANG J H, LU C L, SHANG Z G, et al. P42.3 gene expression in gastric cancer cell and its protein regulatory network analysis[J]. Theoretical biology and medical modelling, 2012, 11(9): 53. (0)
[5]
王昕, 毛炳蔚, 王福伟, 等. 蛋白质空间结构的统计分析[J]. 山西大同大学学报(自然科学版), 2008, 24(5): 3-8. (0)
[6]
章社生, 何康, 范宁, 等. 蛋白质空间结构数字特性统计分析及应用[J]. 武汉工程大学学报, 2010, 32(5): 45-48. (0)
[7]
何立群, 占永平. 感知器神经网络模型研究[J]. 九江学院学报(自然科学版), 2014(4): 37-43. (0)
[8]
ATLAS K. 神经网络的优化与用于优化的神经网络[D]. 大连: 大连理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013197371.htm (0)
[9]
高华龙. 蛋白质空间结构相似性比较方法研究[D]. 大连: 大连交通大学, 2012. http://d.wanfangdata.com.cn/Thesis/Y1583884 (0)
[10]
HAO Y, FAN T, NAN K. Optimization and corroboration of the regulatory pathway of p42.3 protein in the pathogenesis of gastric carcinoma[J]. Computational and mathematical methods in medicine, 2015, 5(28): 1-9. (0)
[11]
KOTLOVYI V, NICHOLS W L, TEN EYCK LF. Protein structural alignment for detection of maximally conserved regions[J]. Biophysical chemistry, 2003, 105(2/3): 595-608. (0)
[12]
徐占, 董洪伟. 多特征框架下的蛋白质相似性比较与分类[J]. 图学学报, 2010, 31(1): 191-196. (0)
[13]
张萍萍, 张建华, 尹咪咪. 蛋白质空间结构相似度多参数算法模型的建立[J]. 郑州大学学报(理学版), 2016, 48(2): 105-109. (0)
[14]
张睿. 计算智能方法及应用研究[J]. 电脑开发与应用, 2012, 25(10): 1-3. DOI:10.3969/j.issn.1003-5850.2012.10.001 (0)
[15]
徐国恒. 二硫键与蛋白质的结构[J]. 生物学通报, 2010, 45(5): 5-6. (0)