2. 河南省高校计算智能与数据挖掘工程技术研究中心 河南 新乡 453007
2. Engineering Technology Research Center for Computing Intelligence and Data Mining of Henan Province, Xinxiang 453007, China
生物地理学优化(biogeography-based optimization, BBO)算法[1]模拟了自然界物种的迁移行为及生存环境的突变现象,通过群智能方法在解的可行域空间搜索最优解.许多学者从不同角度改进BBO算法以增强其优化性能.文献[2]从算法模型角度针对BBO迁移算子提出了6种不同的迁移模型,证明了采用余弦迁移模型的BBO算法优化性能最佳;文献[3]从算法拓扑结构角度将随机环形拓扑结构用于BBO,形成PRBBO,并验证了PRBBO算法的优化性能;文献[4]从算法种群更新方式角度将多源策略和正交学习策略融入BBO,形成POLBBO,并证明了POLBBO算法增强了原算法的优化性能;文献[5]从算法混合角度将BBO与BFO进行混合,并将混合算法用于彩色图像分割,得到了较好的分割效果.目前BBO的相关改进研究通常是从多个角度同时改进算法,以求最大化其优化性能.然而,现实中的优化问题往往是种类多样化,复杂度不一的单峰、多峰及不可分离的非线性问题,又相继有更为复杂的优化问题被提出,对算法优化性能的要求也越来越高.目前,BBO及其改进算法在处理一些复杂优化问题时表现出优化性能不足,计算复杂度较高等缺陷.为得到性能更优的算法,本文提出了一种差分变异和交叉迁移的BBO算法(DCBBO).对于BBO的变异算子,用差分扰动操作取代原变异操作,形成差分变异算子,强化其探索能力;对于BBO的迁移算子,用基于维度的垂直交叉操作替换原迁移操作,形成交叉迁移算子,提升其开采能力,注重其探索能力;又将启发式水平交叉操作融入交叉迁移算子中,形成混合交叉迁移算子,进一步提升开采能力,并平衡算法的探索和开采.此外,从多个方面降低了算法的计算复杂度.为验证DCBBO的优化性能,在一组常用基准函数上进行了大量实验,与其他state-of-the-art算法进行了对比.
1 标准的生物地理学优化算法BBO是在生物地理学理论基础上提出的[1].生态系统(种群)HN由N个栖息地组成,N为种群数量.对于求解一个d维优化问题,栖息地Hi(i=1, 2, …, N)的生存适宜度指数变量SIVs=(SIVi1, SIVi2, …, SIVid),表示所求全局优化问题的一个候选解.该栖息地的生存适宜度指数HSI表示该候选解对应的目标函数值.栖息地Hi的迁入率λi、迁出率μi和变异率mi计算公式为
| $ {\lambda _i} = I\left( {1-{S_i}/{S_{\max }}} \right);{\mu _i} = E\left( {{S_i}/{S_{\max }}} \right);{m_i} = {m_{\max }}\left( {1-{P_i}/{P_{\max }}} \right), $ | (1) |
式中:I为最大迁入率;E为最大迁出率;mmax为最大变异概率;Si为Hi当前的物种数量;Smax为最大物种数量;Pi为物种数量概率;Pmax为最大物种数量概率.迁移操作可以实现迁出栖息地与迁入栖息地的信息共享,变异操作实现了对栖息地生存环境的随机性改变,可以分别表示为
| $ {H_i}\left( {SI{V_j}} \right) \leftarrow {H_{SI}}\left( {SI{V_j}} \right), $ | (2) |
| $ {H_k}\left( {SI{V_j}} \right) \leftarrow l{b_j} + rand\left( {u{b_j}-l{b_j}} \right), $ | (3) |
式中:Hi为迁入栖息地;HSI为通过轮赌选择法选出的迁出栖息地;Hk为变异栖息地;Hi(SIVj)为Hi的第j个SIV;ubj和lbj分别为第j个SIV取值的上限和下限;rand为(0, 1)之间的随机实数.BBO总流程如下.
Step 1:设置相关参数,随机初始化种群;
Step 2:评价每个栖息地的HSI,根据HSI由优至劣对种群排序;
Step 3:计算每个栖息地的迁入率、迁出率和变异率,保留精英栖息地;
Step 4:执行迁移算子;
Step 5:执行变异算子;
Step 6:对每个栖息地进行越界限制;
Step 7:评价每个栖息地的HSI,根据HSI由优至劣对种群排序,用精英栖息地替换较差的栖息地;
Step 8:根据HSI由优至劣对种群排序;
Step 9:判断是否满足算法停止条件,若是则输出最优解,否则返回Step 3.
2 改进的生物地理学优化算法 2.1 差分变异算子差分进化(DE)算法的差分操作具有优秀的探索能力,已被很多其他改进算法所借鉴[6].受DE启发,提出一种差分扰动操作替换BBO的原变异操作,形成差分变异算子.差分扰动操作表示为
| $ {H_i}\left( {SI{V_j}} \right) \leftarrow {H_{rn1}}\left( {SI{V_j}} \right) + \\ {\alpha _d}*\left( {{H_{{\rm{best}}}}\left( {SI{V_j}} \right)-{H_i}\left( {SI{V_j}} \right) + {H_{rn2}}\left( {SI{V_j}} \right)-{H_{rn3}}\left( {SI{V_j}} \right)} \right), $ | (4) |
式中:Hbest为当前迭代种群中HSI最优的栖息地;Hrn1、Hrn2和Hrn3是随机选择的3个栖息地,满足rn1、rn2、rn3和i∈[1, N]且rn1≠rn2≠rn3≠i; 差分缩放因子αd=rand.从式(4)可以看出,变异栖息地Hi的SIV与其他3个不同栖息地对应的SIV通过差分计算得到差分向量,将差分向量赋予权值加到另一个随机选择的栖息地对应的SIV上,生成携带多样化信息的变异SIV.令变异栖息地接受变异SIV,增加了种群多样性,大幅度强化了探索能力.
此外,对于栖息地的变异率采用线性降方法进行计算,使每次迭代所有栖息地都采用相同的变异率,相较于BBO原变异率计算方式,大幅度降低了计算复杂度,其计算公式为
| $ {p_m} = {p_{m\;\max }}-\left( {{p_{m\;\max }}-{p_{m\;\min }}} \right)*t/D{T_{\max }}, $ | (5) |
式中:pm为变异率;t为当前迭代次数;DTmax为最大迭代次数;pm max和pm min分别为pm取值的上限和下限.
2.2 交叉迁移算子BBO的迁移算子开采能力不足,为此,用基于维度的垂直交叉操作取代其迁移算子的直接取代式迁移操作,形成交叉迁移算子,克服原迁移操作迁移形式简单,方向单一,在解空间中可搜索到的位置较为局限的缺陷.基于维度的垂直交叉操作可以表示为
| $ {H_i}\left( {SI{V_j}} \right) \leftarrow {\alpha _c}*{H_{SI}}\left( {SI{V_j}} \right) + \left( {1-{\alpha _c}} \right)*{H_{SI}}\left( {SI{V_{num}}} \right), num = rand*d, $ | (6) |
式中:垂直交叉缩放因子αc=rand.从式(6)可以看出,迁入栖息地Hi的SIV受到迁出栖息地对应的SIV及随机的SIV两者的共同影响,对两者进行加权的交叉计算,并分享给迁入栖息地,使迁入栖息地迅速向迁出栖息地方向聚集,并对迁出栖息地所在解空间区域位置的附近区域进行搜索,从而增强算法的开采能力.又由于迁出栖息地的随机SIV在选择上具有一定的多样性,从而也注重了探索能力.
此外,对于迁出栖息地HSI的选择,用榜样学习法替换算法原轮赌选择法,有利于算法性能的进一步提升,并降低了计算复杂度[7].
2.3 混合交叉迁移算子由于上述改进重点强化算法的探索能力,对开采能力提升不足,为平衡算法的探索和开采,将启发式水平交叉操作融入交叉迁移算子中,形成混合交叉迁移算子.启发式水平交叉操作可以表示为
| $ {H_i}\left( {SI{V_j}} \right) \leftarrow {H_{SI}}\left( {SI{V_j}} \right) + {\alpha _h}*\left( {0.5-rand} \right)*\left( {{H_{SI}}\left( {SI{V_j}} \right)-{H_i}\left( {SI{V_j}} \right)} \right), $ | (7) |
式中:水平交叉缩放因子αh=rand.由式(7)可知,αh*(0.5-rand)*(HSI(SIVj)-Hi(SIVj))可以得到一个扰动值,其扰动方向和幅度分别受(0.5-rand)的结果及αh的取值影响动态变化.将该扰动值加到HSI(SIVj)上,实现了在HSI(SIVj)附近范围随机局部搜索,其搜索方向多样化且幅度不固定.由于榜样学习法选出的迁出栖息地HSI本身比迁入栖息地Hi更优,其所在解空间区域的位置更靠近最优解,所以启发式水平交叉操作实质上是在最优解可能存在的区域小范围多方向局部搜索,从而有效地提升了算法的开采能力.
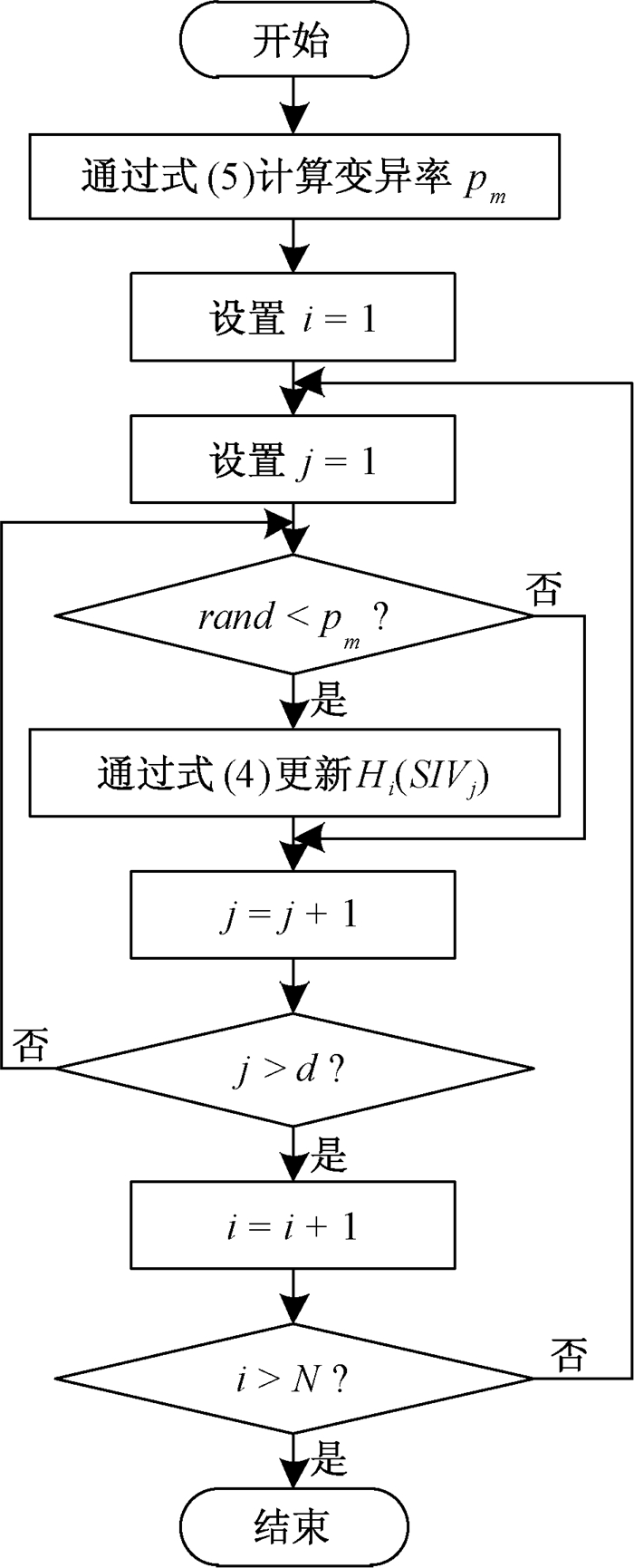
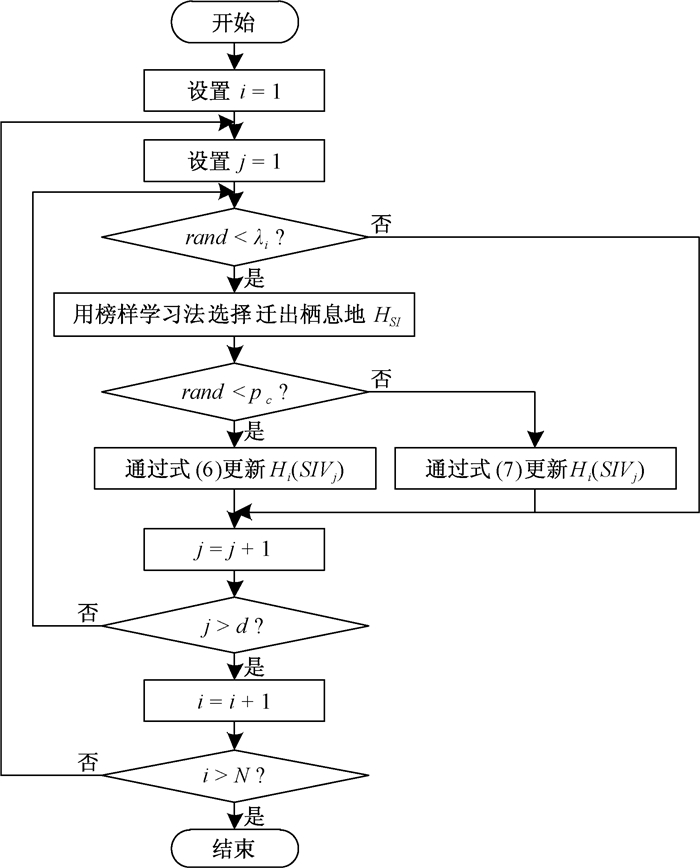
2.4 DCBBO总流程除上述改进外,还将BBO的精英保留策略换成了贪婪选择法[7],将迁入率计算步骤移至算法的迭代循环外[8],进一步降低了算法的计算复杂度,最终形成了DCBBO.差分变异算子的流程如图 1所示, 混合交叉迁移算子的流程如图 2所示.DCBBO总流程如下.
|
图 1 差分变异算子的流程 Figure 1 Flow chart of differential mutation operator |
|
图 2 混合交叉迁移算子的流程 Figure 2 Flow chart of hybrid cross migration operator |
Step 1:设置相关参数,随机初始化种群;
Step 2:评价每个栖息地的HSI,按HSI由优至劣对种群排序;
Step 3:计算每个栖息地的迁入率;
Step 4:执行差分变异算子;
Step 5:执行混合交叉迁移算子;
Step 6:对每个栖息地进行越界限制;
Step 7:评价每个栖息地的HSI,执行贪婪选择法;
Step 8:按HSI由优至劣对种群排序;
Step 9:判断是否满足算法停止条件,若是则输出最优解,否则返回Step 4.
3 实验与分析为验证DCBBO的优化性能,在表 1所示的一组常用基准函数上进行了大量实验,这些基准函数的表达式可以参看文献[9-11].设置DCBBO的种群数量N=20,最大迁入率I=1(由于使用了榜样学习,无需设置最大迁出率),交叉选择概率pc=0.2,pm取值的上界和下界分别为pm max=0.1,pm min=0.001.这些参数取值是通过大量的实验确定的,可以使算法性能最佳.DCBBO以最大迭代次数作为停止条件,根据基准函数维度的不同动态调整,在30维基准函数的实验中,设置DTmax=2 500,其最大函数评价次数(MNFE)为50 000,在50维基准函数的实验中,设置DTmax=4 000,其MNFE为80 000.所有实验均在操作系统为Windows 7、CPU为主频3.10 GHz和内存为4 GB的PC上进行,编程语言采用Matlab R2014a.
|
|
表 1 基准函数 Table 1 Benchmark functions |
本组实验用DCBBO对比了state-of-the-art同类算法,对比算法包括EBO[9]、BBO-M[12]和LBBO[13].这3种对比算法都是近几年提出的BBO改进算法,具有很强的竞争性.为公平起见,设置3种对比算法的种群数量N和最大迭代次数DTmax与DCBBO相同,使它们的MNFE相等,其他参数设置同其相应的参考文献.为避免偶然结果,每种算法在每个基准函数上分别独立运行30次,得到平均值(Mean)、标准差值(Std)及运行时间(t).算法获得的平均值越小表明算法的优化能力越强,获得的标准差值越小表明算法的稳定性越强,消耗的运行时间越少表明算法的运行速度越快.几种算法的结果对比如表 2所示.
|
|
表 2 DCBBO与EBO、BBO-M和LBBO的结果对比 Table 2 Result comparisons among DCBBO, EBO, BBO-M and LBBO |
从表 2可以看出,在30维基准函数的实验中,DCBBO获得的优化能力和稳定性总是优于其他3种算法,DCBBO的运行速度也是3种算法中最快的,且优势明显.在50维基准函数的实验中,LBBO和DCBBO在f11上得到了相同的结果,其他情况下,DCBBO的各项结果依然是最优的.
为验证实验结果的显著性,对表 2中的数据进行了置信水平α=0.05的双尾t检验,其结果如表 3所示,其中NA表示对比算法的标准差值均为0,无法得到t值和p值,Best、Same和Worst分别表示DCBBO显著优于对比算法、与对比算法无显著差异及显著劣于对比算法的次数.从表 3可以看出,大多数情况下,DCBBO显著优于BBO-M和LBBO,具有95%的置信度.相对来说,虽然EBO表现出较强的竞争性,但该算法没有得到过显著优于DCBBO的结果.
|
|
表 3 DCBBO与EBO、BBO-M和LBBO的t检验结果 Table 3 The t-test results of DCBBO, EBO, BBO-M and LBBO |
本组实验用DCBBO对比了state-of-the-art其他类算法,包括PSO的改进算法RLPSO[10]及DE的改进算法DELLU[11]和JADE[14].为客观比较,3种对比算法的结果分别取自其相应的参考文献,由于不同文献选取的基准函数集不同,故只选取这些算法在同维度、同基准函数上的结果对比.为了使对比结果可靠,令DCBBO的MNFE总是小于3种对比算法,这就意味着DCBBO的优化条件更苛刻.几种算法的结果对比如表 4所示,其中NA表示该数据在原文献中未提供.
|
|
表 4 DCBBO与RLPSO、DELLU和JADE的结果对比(d=30) Table 4 Result comparisons among DCBBO, RLPSO, DELLU and JADE (d=30) |
从表 4可以看出,在MNFE更小的情况下,DCBBO在所有情况下获得的结果都是最优的或者与对比算法并列最优,表明DCBBO的优化能力和稳定性整体上优于对比算法.
3.3 DCBBO的计算复杂度讨论在运行环境相同的前提下,优化算法的计算复杂度主要由两部分组成:一是目标函数的计算复杂度;二是算法自身流程的复杂程度.
本文3.1节的实验中记录了算法的运行时间,因DCBBO和其对比算法的MNFE相等,故DCBBO运行耗时少的主要原因在于其算法流程中从多个方面降低了计算复杂度.以BBO为参照,在算法总流程的对比中,BBO每次迭代需要计算所有栖息地的迁入率和迁出率,总计算次数为2*N*DTmax,DCBBO将栖息地迁入率计算移至迭代循环外,采用的榜样学习法不需要计算迁出率.因此,其在整个算法优化过程中只需对每个栖息地的迁入率计算1次,总计算次数为N.BBO采用精英保留策略,每次迭代需对种群排序2次,DCBBO采用贪婪选择法,每次迭代对种群排序一次.在迁移算子的对比中,BBO采用轮赌选择法,选择迁出栖息地平均计算(1+N)/2次,DCBBO采用榜样学习法,选择迁出栖息地只计算1次.在变异算子的对比中,BBO每次迭代需计算每个栖息地的变异率,DCBBO采用线性降方法,每次迭代对所有栖息地变异率只计算1次.综上所述,DCBBO大幅度降低了计算复杂度,从而具有较快的运行速度.
4 结束语为了增强BBO的优化性能,提出了一种差分变异和交叉迁移的BBO算法(DCBBO),提高了算法的探索能力和开采能力并致力于两者的平衡,从多个方面降低了计算复杂度.在不同维度的一组常用基准函数上进行了大量实验,验证了DCBBO显著的优化性能.
| [1] |
SIMON D. Biogeography-based optimization[J]. IEEE transactions on evolutionary computation, 2008, 12(6): 702-713. DOI:10.1109/TEVC.2008.919004 (  0) 0) |
| [2] |
MA H. An analysis of the equilibrium of migration models for biogeography-based optimization[J]. Information sciences, 2010, 180(18): 3444-3464. DOI:10.1016/j.ins.2010.05.035 (  0) 0) |
| [3] |
FENG Q, LIU S, ZHANG J, et al. Improved biogeography-based optimization with random ring topology and Powell′s method[J]. Applied mathematical modelling, 2017, 41: 630-649. DOI:10.1016/j.apm.2016.09.020 (  0) 0) |
| [4] |
XIONG G, SHI D, DUAN X. Enhancing the performance of biogeography-based optimization using polyphyletic migration operator and orthogonal learning[J]. Computers and operations research, 2014, 41(1): 125-139. (  0) 0) |
| [5] |
张新明, 康强, 涂强, 等. 融合细菌觅食趋化算子的生物地理学优化算法[J]. 郑州大学学报(理学版), 2016, 48(4): 44-53. (  0) 0) |
| [6] |
STORN R, PRICE K. Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 (  0) 0) |
| [7] |
张新明, 尹欣欣, 涂强. 动态迁移和椒盐变异融合生物地理学优化算法的高维多阈值分割[J]. 光学精密工程, 2015, 23(10): 2943-2951. (  0) 0) |
| [8] |
张新明, 涂强, 尹欣欣. 混合迁移的高效BBO算法及其在图像分割中的应用[J]. 计算机科学与探索, 2016, 10(10): 1459-1468. (  0) 0) |
| [9] |
ZHENG Y J, LING H F, XUE J Y. Ecogeography-based optimization: enhancing biogeography-based optimization with ecogeographic barriers and differentiations[J]. Computers and operations research, 2014, 50(10): 115-127. (  0) 0) |
| [10] |
夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法[J]. 计算机学报, 2015, 38(7): 1397-1407. DOI:10.11897/SP.J.1016.2015.01397 (  0) 0) |
| [11] |
周晓根, 张贵军, 郝小虎, 等. 一种基于局部Lipschitz下界估计支撑面的差分进化算法[J]. 计算机学报, 2016, 39(12): 2631-2651. DOI:10.11897/SP.J.1016.2016.02631 (  0) 0) |
| [12] |
NIU Q, ZHANG L, LI K. A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells[J]. Energy conversion and management, 2014, 86: 1173-1185. DOI:10.1016/j.enconman.2014.06.026 (  0) 0) |
| [13] |
SIMON D, OMRAN M G H, CLERC M. Linearized biogeography-based optimization with re-initialization and local search[J]. Information sciences, 2014, 267: 140-157. DOI:10.1016/j.ins.2013.12.048 (  0) 0) |
| [14] |
ZHANG J, SANDERSON A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE transactions on evolutionary computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


