2. 海南大学 信息科学技术学院 海南 海口 570228;
3. 海南大学 南海海洋资源利用国家重点实验室 海南 海口 570228
2. College of Information Science and Technology, Hainan University, Haikou 570228, China;
3. State Key Laboratory of Marine Resource Utilization in South China Sea, Haikou 570228, China
近年来分布式拒绝服务(distributed denial of service,DDoS)攻击方式层出不穷,其频率、规模、危害等快速增长[1].大多数DDoS攻击检测方法趋向于混合检测方法[2],而且结合机器学习模型来提高正确率,包括时间序列模型[3]、支持向量机[4]、遗传算法[5]、神经网络[6]等.尤其针对大数据环境下的DDoS检测方法的研究[7-8]也逐渐增多,但是在大数据环境下正常数据的高流量、多样性和突发性增加了攻击识别的难度,使得DDoS攻击检测方法仍存在较高的误报率、漏报率,亟待提出有效的检测方法.针对该问题,本文提出一种基于网络流组合相关度与决策树参数优化算法的随机森林(random forest, RF) DDoS攻击检测方法.
1 DDoS攻击流特征提取由于DDoS攻击通常采用多对一的攻击模式,网络流的源地址与目的地址、源地址与目的端口、目的端口与目的地址均呈现出多对一的关系,致使攻击呈现出流非对称性的特点[9].在直接或反射DDoS攻击中,攻击流会造成网络服务不正常或瘫痪,使得攻击目标不能正常回复网络服务请求而产生大量只有源地址到目的地址的单向网络流,致使攻击呈现出流半交互性[10].因此本文基于流非对称性和半交互性提取特征.
假设某单位时间T内网络流F为
1) 记源IP地址为Am、目的IP地址为An的所有数据包形成的类为StDIP(Am, An).对上面形成的这些类,若有不同的目的IP地址 An和Ak使得类StDIP(Am, An)和StDIP(Am, Ak)均非空,则删除所有源IP地址为Am的数据包所在的类.假设最后剩下的类为RStD1, RStD2, …, RStDm,定义网络流F的地址相关统计(address correlation statistics, ACS)特征为:
| $ AC{S_F} = \sum\limits_{i = 1}^m {W\left( {RSt{D_i}} \right)} , $ | (1) |
其中: W(RStDi)=αPort(RStDi)+(1-α)Packet(RStDi), 0 < α < 1.Port(RStDi)是类RStDi中不同端口号的个数, Packet(RStDi)是类RStDi中数据包的个数,α是加权值,一般情况下α=0.5.
2) 记源IP地址为Am的所有数据包形成的类为SoIPC(Am),目的IP地址为An的所有数据包形成的类为DeIPC(An).若类SoIPC(Am)的源IP地址Am使得类DeIPC(Am)为空,则称SoIPC(Am)中所有的数据包为一个源半交互流(source half interaction flow, SHI),记为SHI(Am),表示SHI流有源半交互性,SHI(Am)中不同端口号的数量记为Port(SHI(Am)).由此,对SoIPC类分类,得到所有源半交互流SHI,表示为SHI1, SHI2, …, SHIs.
对s个SHI流分类,将目的IP地址相同的SHI流分在同一类别中,记具有不同源IP地址和相同目的IP地址Am的SHI流数量为Msdnm,具有相同目的IP地址Am的SHI流所在类表示为SDHI(Msdnm, Am),且m=1, 2, …, l.假设所有的Msdnm≥M (M≥2,为保证攻击检测较大的覆盖面,本文令M=2)的SDHI类为SDHI1, SDHI2, …, SDHIk,类SDHIi中不同目的端口号的数量表示为Port(SDHIi),i=1, 2, …, k.据此,定义网络流F中单向流半交互度(unidirectional flow semi interaction,UFSI)定义为:
| $ UFS{I_F} = \frac{1}{{f\left( k \right)}}\left( {\sum\limits_{i = 1}^k {\left( {Msd{n_i} + w\left( {Port\left( {SDH{I_i}} \right)} \right)} \right) - k} } \right), $ | (2) |
其中:
3) 结合1)和2)中的两部分特征提取规则,在采样时间Δt内,分别计算和提取ACS和UFSI两种特征来构造二元特征,形成网络流组合相关度(combination correlation degree,CCD):
| $ CC{D_F} = \left( {{w_1}\;AC{S_F}, {w_2}UFS{I_F}} \right), $ | (3) |
其中: w1、w2均表示权重,表示CCD特征中ACS和UFSI所占的比例.
大数据环境下的正常网络流与DDoS攻击流都具有高容量、多样性和突发性的特性,但是CCD特征序列仍然能较好地反映正常流与攻击流的本质区别.首先,该特征中的两部分统计特征均以DDoS攻击的流非对称性为基础提出的,攻击情况下CCD特征值比正常情况下的值显著增大且持续时间较长;其次,ACS特征提取的是“多对一”与“一对一”会话模式的网络流的源IP地址与端口的加权统计特征,排除了“一对多”网络流的干扰,更能较好地反映网络中攻击流与正常流之间的相关性变化,而UFSI特征提取的是网络流中“多对一”会话模式的单向流的统计信息,更能准确地刻画网络受到DDoS攻击时单向流急剧增加的情况.这两方面结合能够准确描述攻击流在受害端汇聚和直接影响正常流的状态变化,以及汇聚的攻击流混杂在正常流中引起的CCD特征序列异常的现象,从而能及时、准确地提取攻击前后网络的相关状态特征,较好地区分攻击前后的网络异常现象.
2 基于CCD的随机森林的DDoS攻击检测方法 2.1 CCD特征序列提取对数据集以采样时间Δt进行流量采样,分别计算各采样时间中ACS和UFSI的值,并整合为二元组合,N次采样后,获得CCD时间序列样本M,M(N, Δt)={CCDi,i=1, 2, …, N},N为序列长度.按照采样时间顺序提取CCD特征序列,Δt作为一个时间单位,则该序列为随时间Δt累加,且长度为N的时间特征序列.
2.2 随机森林模型随机森林作为一种集成学习分类方法,具有准确率较高、能有效防止过拟合、训练速度快、可对变量重要性排序、容易实现并行化等优点.假设随机森林分类器为R(x), 第i棵决策树记为ti(x), R(x)={ti(x), i∈[0, n_estimators]}, 其中:n_estimators表示随机森林中决策树的棵数;x为输入的待分类的训练样本;sign(x)∈S为x的标记值;S为标记类别的集合;ti(x)的输出为S中的某个值,作为单棵决策树对于样本x的估计值;R(x)的输出为{ti(x), i∈[0, n_estimators]}估计值中的众数.在使用随机森林进行攻击检测时,x为CCD特征训练集利用重采样技术随机生成的新训练数据集中的值;在DDoS攻击检测中只有异常与正常两种标记,即S={-1,1},且sign(x)只取-1来代表攻击样本标记和1来代表正常样本标记.本文选取Gini系数作为单棵决策树分裂的量化评价指标.该系数既能反映所有类别样本的比例关系以及不同类别样本的比例变化,还能使各种样本计算的系数值均在(0, 1)之间,以便处理分析.
2.3 基于遗传算法的随机森林参数优化遗传算法(genetic algorithm,GA)可对任意形式的约束和目标函数在全局意义上搜索问题最优解,具有潜在并行性、过程简单和快速随机搜索等优点.综合考虑随机森林本身性能、特征样本数量等,本文设初始种群M为30,进化代数G为50,随机森林子树的棵数n_estimators的整数范围(2,30),子决策树最大深度max_depth整数范围(2,10),变异率Pc、交叉率Pm分别为默认值.选择训练样本K次交叉验证中Roc曲线下的面积(area under curve,AUC)的平均值作为判定种群中个体优劣度的适应度函数值,其表达式由公式(4)所示.该值越大,越接近1,越有利于个体的遗传进化.
| $ Fitness = \frac{1}{K}\sum\limits_{i = 1}^K {AU{C_i}} . $ | (4) |
随机森林中子树的数目和子树的最大深度均会对随机森林的训练结果有关键的影响:过少会导致训练不足而不能产生较好结果;过多会导致构建RF的时间长、规模复杂等问题.因此,选定子树的最大棵数n_estimators和子树的最大深度max_depth作为待优化参数.基于遗传算法的随机森林参数优化算法见算法1.
算法1 基于遗传算法的随机森林参数优化算法.
输入:CCD特征训练集,初始化Pm,Pc,M,G等参数,待优化参数n_estimators,max_depth的范围;
输出:最优参数组合(n_estimators, max_depth).
1.利用初始化Pm,Pc,M,G等参数,随机产生第一代种群Pop;
2. While繁殖代数小于G do
3. 在指定待优化参数范围内随机选取参数组合(n_estimators, max_depth);
4. 基于CCD特征训练集训练指定参数组合的随机森林;
5. 根据公式(4)计算种群Pop中每一个体的适应度Fitness;
6. 初始化空种群newPop;
7. While M个子代被创建do
8. 根据适应度以轮盘选择算法从种群Pop中选出2个个体;
9. If random (0, 1) < Pm then
10. 对2个个体按交叉概率Pc执行交叉操作;
11. If random (0, 1) < Pm then
12. 对2个个体按变异概率Pm执行变异操作;
13. End while
14. 将M个子代加入种群newPop中;
15. 用newPop取代Pop;
16.End while
17.选出最终代Pop中适应度值最优的个体,提取其中最优参数组合;
18. return参数组合(n_estimators, max_depth).
2.4 基于CCD的随机森林DDoS攻击检测根据前文描述,本文基于CCD特征序列优化了参数,训练了RF分类器,得到了基于CCD的遗传算法优化的随机森林(genetic algorithm-optimized random forest, GAORF)的DDoS攻击检测模型.
基于CCD的随机森林DDoS攻击检测方法识别DDoS攻击流程如图 1所示.该模型为只需判定攻击与否二分类问题,假设正常情况下设置检测模型输出标记为1,而在受到攻击情况下CCD特征值会不同程度地变化,则模型输出值不同于正常情况,设置检测模型输出标记为-1.判断待测网络流是否异常需将待测网络流CCD特征序列输入攻击检测模型,若所输出的标记值为-1则为攻击.
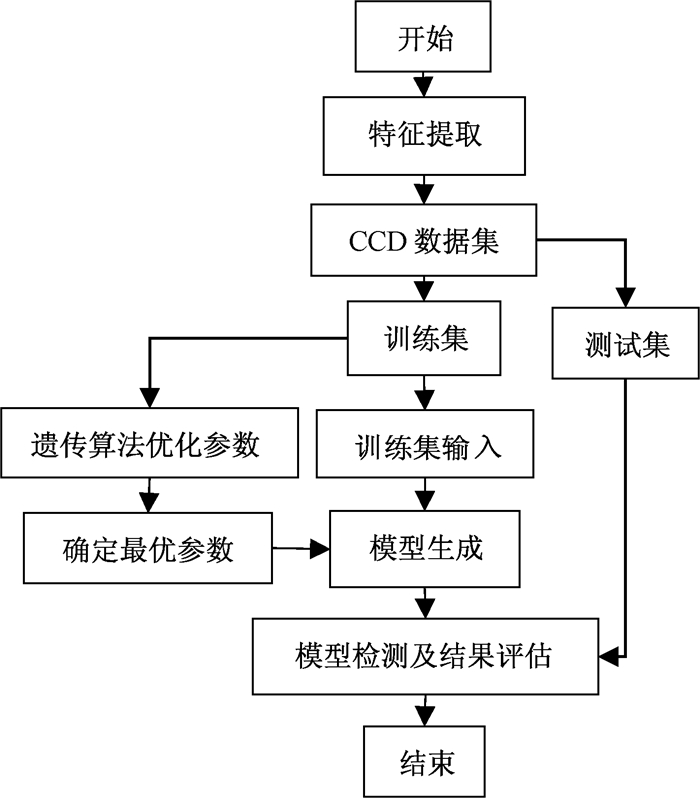
|
图 1 基于CCD的GAORF-DDoS攻击检测方法的流程 Fig. 1 Process of GAORF-DDoS attack-detection method based on CCD |
本文前面已分析得出CCD特征序列能较好地反映大数据环境下正常流与DDoS攻击流的不同状态特征.RF集成了多棵决策树,并使用bootstrap方法缩小单棵决策树训练样本集的大小,使用投票机制选取更加合理的分类结果,而且本文提出的基于遗传算法的RF参数优化算法有效地提高了RF的分类能力.因此本文提出基于CCD的GAORF的DDoS攻击检测方法,可以快速有效地识别大数据环境下的DDoS攻击.
3 实验结果与分析本文实验使用CAIDA “DDoS attack 2007”数据集[11],检测性能评判指标包括准确率(accuracy)、漏报率(missing report rate, MR)、误报率(false alarm rate, FR).设采样间隔Δt=0.1 s,ACS的权重w1=0.1,UFSI的权重w2=0.6,其中w1(0 < w1≤1)、w2(0 < w2≤1)是利用本文检测方法通过不断变化权重大小对样本进行学习实验并依据最佳识别效果来选取的.选取训练集和测试集并做归一化处理,基于训练集利用遗传算法对RF中子决策树最大棵数和最大深度进行了优化.根据初始种群规模、训练样本数量及迭代时间的考虑,选取了五折交叉验证的平均AUC作为适应度函数来进行寻优操作,即选定公式(4)中交叉验证折数K=5.确定RF检测模型的子树棵数和最大深度两个待优化参数的值.将参数优化的RF模型对训练数据集进行训练形成检测模型,应用该模型对测试集进行检测,并对结果进行了分析.
3.1 攻击特征比较分析本文分别对ACS、UFSI和CCD特征进行了多组实验对比分析:假定攻击流不变,每组实验依次将正常流缩小至原值的1/10,以模拟攻击流发生作用引起正常流不断减少的情况;假定正常流不变,每组实验依次将攻击流缩小至原值的1/10,以模拟攻击流模仿正常流状态变化减少攻击流来逃避检测的情况.从相同训练集中分别提取ACS、UFSI和CCD特征等3种特征,并分别基于3种特征训练RF模型生成3种分类器,再利用相同测试集对3种分类器进行测试,以比较3种特征对正常流和攻击流的区分能力,测试结果如图 2和图 3所示.其中CCD_MR、ACS_MR、UFSI_MR分别为基于CCD特征、基于ACS特征、基于UFSI特征的检测方法的漏报率;CCD_FR、ACS_FR、UFSI_FR分别为基于CCD特征、基于ACS特征、基于UFSI特征的检测方法的误报率.如图 2所示,随着正常流减少,3种特征均能较好地识别攻击,其中CCD特征表现最好.从漏报率来看,随着正常样本减小,CCD_MR下降至15%,较ACS_MR和UFSI_MR低2%左右,且有明显下降趋势.对误报率而言,随着正常样本减少,3种检测方法的误报率(ACS_FR、UFSI_FR、CCD_FR)虽有微弱上升,但均保持在2%左右.图 3中,随着攻击流减少,分别基于3种特征的检测方法的误报率和漏报率都没有大幅度改变,其中CCD特征表现也最好.由于ACS特征统计“多对一”和“一对一”的网络流,其中包含了正常流,故其值会随着正常流的减少而发生相应变化,即ACS特征能较好地反映攻击流引起的正常流状态异常变化,因此漏报率较低.因正常流中“多对一”的单向流相对较少,故当正常流减少时,UFSI特征值发生细微变化,即UFSI特征能较好地反映攻击产生的“多对一”单向流的半交互性,因此误报率较低.由于CCD特征中包含了ACS特征和UFSI特征提供的两方面统计信息,故基于CCD特征检测的漏报率和误报率都较低,相对ACS特征和UFSI特征,CCD特征能够更好地识别DDoS攻击.
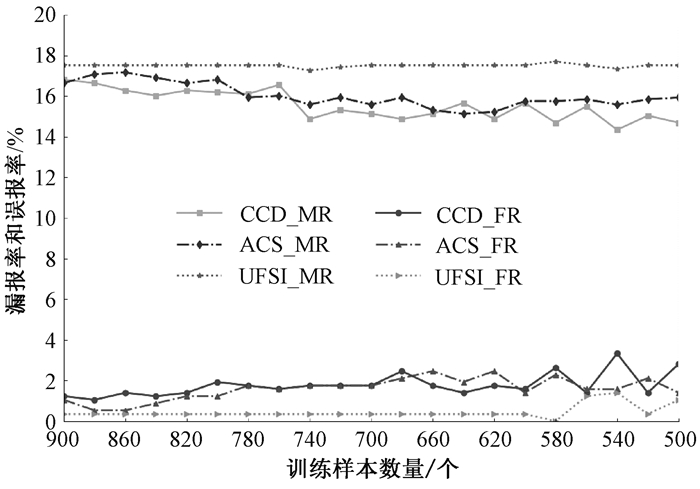
|
图 2 正常训练样本变化中特征对比的误报率和漏报率 Fig. 2 The false alarm rate and missing alarm rate of feature contrast with changing normal training samples |
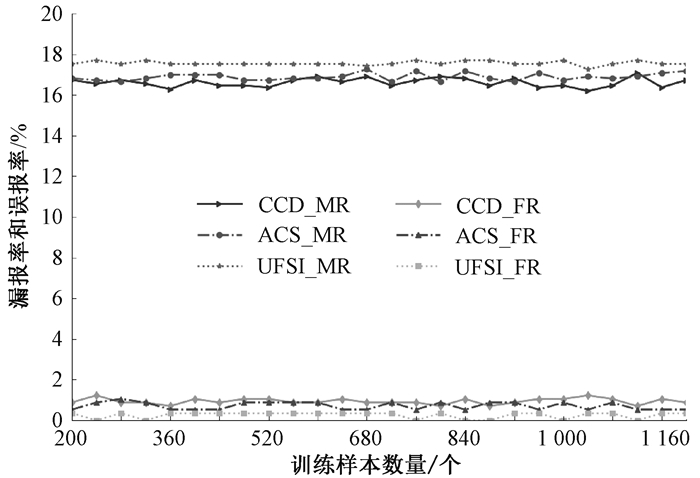
|
图 3 攻击训练样本变化中特征对比的误报率和漏报率 Fig. 3 The false alarm rate and missing alarm rate of feature contrast with changing attack training samples |
考虑到支持向量机(support vector machine,SVM)分类模型是机器学习领域中的主流方法,本文将提出的GAORF分类模型与nu-SVM、C-SVM和一类支持向量机(one-class-SVM)等3种分类模型进行了多组DDoS攻击检测实验对比.本实验将从数据集样本中提取的CCD特征序列分别带入了GAORF、nu-SVM、C-SVM和one-class-SVM 4种分类模型进行训练和测试,各组实验分别通过不断改变正常训练样本数量和攻击训练样本数量来比较各种分类模型的学习分类能力和鲁棒性,其中选取了攻击早期的数据作为部分测试样本.实验结果如表 1和表 2所示.
|
|
表 1 正常训练样本数量变化中4种算法检测对比结果 Tab. 1 Comparison of four algorithms with changing numbers of normal training samples |
|
|
表 2 攻击训练样本数量变化中4种算法检测对比结果 Tab. 2 Comparison of four algorithms with changing numbers of attack training samples |
由表 1可知,随着正常训练样本的增大,GAORF分类模型的准确率保持在90%以上,误报率保持在0.4%以下,漏报率保持在15.6%以下.一方面RF本身具有良好稳定的分类性能,能较好地挖掘和利用CCD特征对攻击引起的正常流状态异常变化的表征能力;另一方面基于遗传算法的RF参数优化算法通过学习正常训练样本集优化了RF参数,提高了RF分类能力,因此GAORF分类模型的分类效果最好.表 1中nu-SVM模型的漏报率和误报率波动较大,准确率在87.6%以下且浮动较大.由于测试集中包含了攻击早期攻击特征值较低的部分数据,这部分特征值与正常流特征值相近,致使nu-SVM模型分类超平面难以区分从而影响了检测结果.C-SVM分类模型在正常训练样本数量大于500时,准确率和漏报率分别保持在91.6%和16%,但是正常训练样本数量为400时该模型出现误报率为100%的情况.由于该模型中惩罚参数并不会因为训练样本数量过度增加而有所改变,使模型表现出了较好的稳定性;但是当正常样本较少时,该模型难以获得最优分类面,使其出现了误报率骤增的情况.随着正常训练样本的增大,虽然one-class-SVM方法保持了较低的漏报率,但比其他方法误报率高,使其准确率均在70%以下.其原因为one-class-SVM只能训练正常训练样本生成分类模型,致使识别攻击比较困难,因此难以取得较为理想的分类效果.
表 2显示,在变化攻击样本增大时,GAORF模型的检测结果与其他3种SVM相比仍有很好表现,保持了91%以上的准确率,15%的较低漏报率.一方面RF本身具有良好的稳定分类性能,能较好地挖掘和利用CCD特征对攻击流特性的表征能力;另一方面基于遗传算法的RF参数优化算法通过学习攻击训练样本集优化了RF参数,提高了RF分类能力.因此4种分类模型中GAORF分类模型的分类效果仍然最好.C-SVM模型在检测中保持91.6%的准确率,在攻击训练样本数量大于500之后,C-SVM模型仍有16%以上较高漏报率.由于C-SVM模型在对攻击训练样本充分拟合之后,值较大的攻击样本并未影响超平面,从而降低了C-SVM模型的分类能力.随着攻击训练样本的增大,nu-SVM分类模型的漏报率波动较大,准确率较低.其原因主要是当正常训练样本不变而攻击样本增大时,会使得超平面有所偏移,使得该模型难以准确识别测试集中部分攻击早期特征值较低的样本.one-class-SVM检测模型的准确率保持在70%以下,误报率较高.由于该模型只对正常训练样本进行训练,增加攻击训练样本并不能改变其分类模型,因此分类结果未变.
综合表 1和表 2可知,针对正常样本和攻击样本的不断变化,GAORF分类模型比各种经典的SVM分类模型具有更强的学习分类能力和鲁棒性.尤其在大数据环境下,样本特征维数和数据集规模日益增长,较SVM分类模型,RF更能适应大数据的要求.
4 结论针对大数据环境下DDoS攻击检测方法存在误报率、漏报率高的问题,本文提出了一种基于组合相关度的随机森林的DDoS攻击检测方法.首先定义了网络流组合相关度CCD,该特征采用地址相关统计特征ACS和单向流半交互度UFSI来表征攻击流的非对称性和半交互性.本文提出的基于CCD的遗传算法的参数优化算法来优化RF参数,并进行分类训练以生成DDoS攻击分类模型来检测攻击.实验表明,本文定义的CCD特征能较好地提取攻击流特性及其引起的正常流状态异常变化特征,提出的检测方法比同类检测方法有更高的准确率,更低的误报率和漏报率,较好的鲁棒性,能在大数据环境下有效地检测DDoS攻击.
| [1] |
BEHAL S, KUMAR K. Characterization and comparison of DDoS attack tools and traffic generators:a review[J]. International journal of network security, 2017, 19(3): 383-393. (  0) 0) |
| [2] |
AGRAWAL S, AGRAWAL J. Survey on anomaly detection using data mining techniques[J]. Procedia computer science, 2015, 60(1): 708-713. (  0) 0) |
| [3] |
CHENG J, ZHOU J H, LIU Q, et al. A DDoS detection method for socially aware networking based on forecasting fusion feature sequence[J]. The computer journal, 2018, 61(7): 959-970. DOI:10.1093/comjnl/bxy025 (  0) 0) |
| [4] |
WANG C, ZHENG J, LI X. Research on DDoS attacks detection based on RDF-SVM[C]//International Conference on Intelligent Computation Technology and Automation. Changsha, 2017: 161-165.
(  0) 0) |
| [5] |
UDDIN M, ALSAQOUR R, ABDELHAQ M. Intrusion detection system to detect DDoS attack in gnutella hybrid P2P network[J]. Indian journal of science & technology, 2013, 6(2): 4045-4057. (  0) 0) |
| [6] |
RIADI I, MUHAMMAD A W, SUNARDI. Neural network based DDoS detection regarding hidden layer variation[J]. Journal of theoretical & applied information technology, 2017, 95(15): 3684-3691. (  0) 0) |
| [7] |
SINGH K, GUNTUKU S C, THAKUR A, et al. Big data analytics framework for peer-to-peer botnet detection using random forests[J]. Information sciences, 2014, 278(19): 488-497. (  0) 0) |
| [8] |
CHENG J, XU R M, TANG X Y, et al. An abnormal network flow feature sequence prediction approach for DDoS attacks detection in big data environment[J]. Computers, materials & continua, 2018, 55(1): 95-119. (  0) 0) |
| [9] |
程杰仁, 殷建平, 刘运, 等. 基于地址相关度的分布式拒绝服务攻击检测方法[J]. 计算机研究与发展, 2009, 46(8): 1334-1340. (  0) 0) |
| [10] |
CHENG J, TANG X, YIN J. A change-point DDoS attack detection method based on half interaction anomaly degree[J]. International journal of autonomous & adaptive communications systems, 2017, 10(1): 38-54. (  0) 0) |
| [11] |
THE COOPERATIVE ASSOCIATION FOR INTERNET DATA ANALYSIS. The Caida Ucsd "DDoS attack 2007" dataset[EB/OL]. (2007-08-05)[2018-08-01]. http://www.caida.org/data/passive/ddos-20070804_dataset.xml.
(  0) 0) |
 2019, Vol. 51
2019, Vol. 51


