0 引言

群智能优化算法是通过模拟自然界中的一些机制，并建立其数学模型的元启发式算法。群智能优化算法针对优化问题表现出了较强的有效性及鲁棒性，因此越来越多的学者对元启发式算法进行了研究，近几年提出的算法有鲸鱼优化算法(whale optimization algorithm, WOA)^[1]、花卉授粉算法(flower pollination algorithm, FPA)^[2]、蝴蝶优化算法(butterfly optimization algorithm, BOA)^[3]、正弦优化算法(sine cosine algorithm, SCA)^[4]、麻雀搜索算法(sparrow search algorithm, SSA)^[5]和哈里斯鹰优化算法(Harris Hawks optimization, HHO)^[6]等。并且群智能优化算法在机器人路径规划^[7]、图像匹配^[8]和特征选择^[9]等领域，表现出了优秀的性能。HHO是Heidari等^[6]提出的一种新型群智能优化算法，它仿照自然界中哈里斯鹰的捕食行为，分为探索与开发两种阶段，又根据猎物是否逃脱等情况将开发行为细分为四种策略进行局部搜索。该算法具有寻优能力强、参数少、原理简单等优点，但仍具有容易早熟收敛、寻优精度较差、全局搜索能力较弱的问题。

针对上述存在的问题，已有研究人员对其进行改进。文献[10]引入长时记忆序列的概念，防止算法陷入局部最优。文献[11]利用Fuch无限折叠混沌策略初始化种群, 在探索阶段引入黄金正弦算子，利用透镜成像学习和柯西变异策略进行扰动。文献[12]设计了基于方形领域的多子群拓扑结构，利用原有策略在纵向和横向中进行迭代。文献[13]利用精英等级制度增强个体间信息交流，采用Tent混沌映射调整随机值，将逃逸能量改进为非线性形式，最后利用高斯游走进行扰动。文献[14]利用交叉和变异的进化算子来提高HHO算法的性能，并用对立学习和随机对立学习平衡算法的全局开发与局部搜索。文献[15]利用Tent混沌映射初始化种群，之后提出优化参数的勘探系数来提高勘探能力，最后利用随机游走策略，进一步增强算法的开发能力。文献[16]将逃逸能量改进为非线性形式，引入自适应权值的策略，最后通过相对反射的策略进一步改进了HHO算法。

综上所述，已有的改进策略在一定程度上增强了算法的寻优能力，但仍有一定的提升空间。本文针对上述问题，提出融合多策略改进的哈里斯鹰算法(improved Harris Hawks optimization fused with multiple strategies, IHHO)，从以下几个方面进行改进：1) 采用佳点集初始化种群，使种群的多样性和遍历性进一步提升；2) 重新设置算法进行探索或开发的条件，更好地平衡算法的全局搜索与局部搜索能力；3) 利用麻雀算法中发现者更新公式对探索阶段位置公式进行改进，提升算法全局搜索能力；4) 针对每次迭代中最优个体进行柯西变异和高斯变异扰动，防止算法陷入局部最优。

1 哈里斯鹰优化算法

哈里斯鹰算法作为一种元启发式算法，仿照自然界中哈里斯鹰捕食的策略进行寻优操作。算法分为探索和开发两个阶段，主要依据逃逸能量E来进行转化，其计算公式为

$ E=2 E_{0}(1-t / T), E_{0}=2 r-1, $

(1)

其中：t为当前迭代次数；T为最大迭代次数；r为[0, 1]间的随机数。

1.1 探索阶段

当逃逸能量$|E| \geqslant 1$时，算法进入探索阶段，进行广泛的搜索操作。位置更新公式为

$ \begin{aligned} & \boldsymbol{X}(t+1)= \\ & \begin{cases}\boldsymbol{X}_k(t)-r_1\left|\boldsymbol{X}_k(t)-2 r_2 \boldsymbol{X}(t)\right|, & q \geqslant 0.5, \\ \left(\boldsymbol{X}_r(t)-\boldsymbol{X}_{m}(t)\right)-r_3\left(l b-r_4(u b-l b)\right), & q <0.5, \end{cases} \\ & \boldsymbol{X}_{m}(t)=\frac{1}{N} \sum\limits_{i=1}^N \boldsymbol{X}_i(t), \end{aligned} $

(2)

其中: $\boldsymbol{X}_{k}$为在种群中随机选择的个体; $\boldsymbol{X}_{r}$为猎物位置, 即当前最优个体; $\boldsymbol{X}_{m}$为当前种群平均位置; $N$为种群中个体数量; $r_{1} 、r_{2} 、r_{3} 、r_{4}$为四个独立的均匀分布的随机数, 取值为$[0, 1] ; l b$和$u b$分别为问题的下界和上界。

1.2 开发阶段

当逃逸能量$|E|<1$时，算法进入开发阶段，进行精细的局部搜索。此时根据逃逸能量的值和猎物是否逃脱，选择四种不同的局部搜索策略进行位置更新。猎物是否逃脱根据随机值r进行判断。

当逃逸能量$|E| \geqslant 0.5$, 且$r \geqslant 0.5$时，采取软包围的策略进行位置更新，方法为

$ \begin{aligned} & \boldsymbol{X}(t+1)=\Delta \boldsymbol{X}(t)-E\left|\boldsymbol{J}\boldsymbol{X}_{r}(t)-\boldsymbol{X}(t)\right|, \\ & \Delta \boldsymbol{X}(t)=\boldsymbol{X}_{r}-\boldsymbol{X}(t), \end{aligned} $

(3)

其中：J为跳跃能量，其值为[0, 2]的随机数；$\Delta \boldsymbol{X}(t)$表示在第$t$次迭代中最优个体与当前个体间位置的距离。

当$|E|<0.5$, 且$r \geqslant 0.5$时，猎物逃逸失败，此时采用硬包围策略进行位置更新，公式为

$ \boldsymbol{X}(t+1)=\boldsymbol{X}_{r}(t)-E|\Delta \boldsymbol{X}(t)| \text { 。} $

(4)

当$|E| \geqslant 0.5$, 且$r <0.5$时, 算法采用渐进式快速俯冲软包围的策略进行更新, 若使用位置$\boldsymbol{Y}$更新后适应度未改善, 则采用位置$\boldsymbol{Z}$更新, 若适应度值还未得到改善, 则保留原位置, 其具体公式为

$ \boldsymbol{X}(t+1)= \begin{cases}\boldsymbol{Y}, & F(\boldsymbol{Y})<F(\boldsymbol{X}(t)), \\ \boldsymbol{Z}, & F(\boldsymbol{Z})<F(\boldsymbol{X}(t)), \end{cases} $

(5)

$ \begin{gathered} \boldsymbol{Y}=\boldsymbol{X}_{r}(t)-E\left|\boldsymbol{J} \boldsymbol{X}_{r}(t)-\boldsymbol{X}(t)\right|, \\ \boldsymbol{Z}=\boldsymbol{Y}+\boldsymbol{S} \times Leavy(D), \\ L_{F}(x)=0.01 \times(u \times \sigma) /\left(|v|^{\frac{1}{\beta}}\right), \\ \sigma=\left[\Gamma(1+\beta) \times \sin \left(\frac{{\rm{ \mathsf{ π} }} \beta}{2}\right) / \Gamma\left(\frac{1+\beta}{2}\right) \times \beta \times 2^{\frac{\beta-1}{2}}\right]^{\frac{1}{\beta}}, \end{gathered} $

其中：D是问题的维度；S是大小为1×D的随机向量；Leavy是莱维飞行函数；u、v是在(0, 1)间均匀分布的随机数；β为默认常数，设置为1.5；Γ为伽马函数。

当$|E|<0.5$, 且$r <0.5$时，采取渐进式快速俯冲硬包围策略进行位置更新，此时，种群不断缩小最优位置与平均位置之间的距离进行寻优，公式为

$ \boldsymbol{Y}=\boldsymbol{X}_{r}(t)-E\left|\boldsymbol{J}\boldsymbol{X}_{r}(t)-\boldsymbol{X}_{m}(t)\right|, $

(6)

若采用位置$\boldsymbol{Y}$后适应度值得到改善, 则位置更新为$\boldsymbol{Y}$, 否则采用$\boldsymbol{Z}$位置, 若失败则返回原位置。

2 改进的哈里斯鹰优化算法 2.1 佳点集初始化种群

在智能优化算法中，初始解的质量会对搜索结果产生一定的影响。由于系统产生的随机数并不是完全随机的，所以存在分布不均匀、容易聚集等缺点。因此为了尽可能使数值在搜索空间中均匀分散，提高初始解的遍历性，本文采用佳点集^[17]来初始化种群。佳点集由数学家华罗庚提出，设$\boldsymbol{G}_{s}$是$s$维空间中的单位立方体, 若$r \in \boldsymbol{G}_{s}$, 形为

$ \boldsymbol{P}_{n}(k)=\left\{\left(\left\{r_{1}^{(n)} * k\right\}, \cdots, \left\{r_{s}^{(n)} * k\right\}\right), 1 \leqslant k \leqslant n\right\}, $

偏差为$\varphi(n)=C(r, \varepsilon) n^{-1+\varepsilon}$, 其中$C(r, \varepsilon)$是与$r$和$\varepsilon$有关的常数, 则$P_{n}(k)$为佳点集。令$\boldsymbol{r}=$ $\{2 \cos (2 {\rm{ \mathsf{ π} }} k / p), 1 \leqslant k \leqslant s\}$, 其中: $p$是满足$(p-$ $3) / 2 \geqslant s$的最小素数, 将$r$称为佳点。生成佳点集后, 将其映射到搜索空间中的公式为

$ X_{i, j}=(u b-l b) \cdot\left\{r_{j}^{(i)} \cdot k\right\}+l b \text { 。} $

(7)

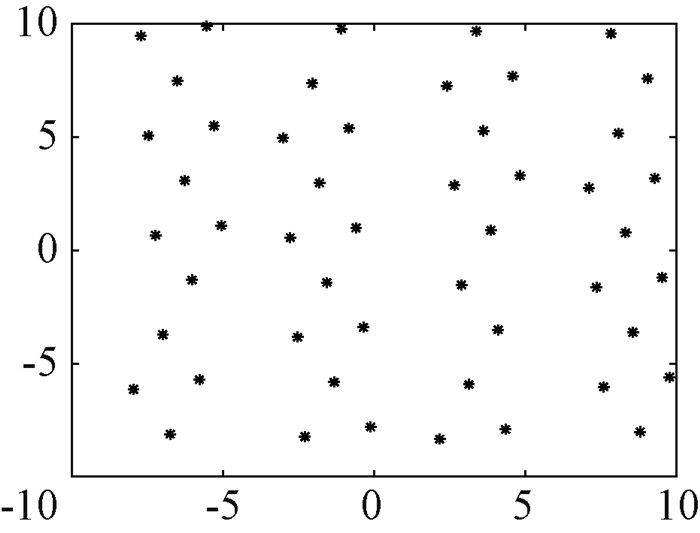
由图 1可知，假设种群数量为50，与传统初始化种群方式相比，佳点集生成的初始种群分布更均匀，能够保留更多的信息，为之后算法的寻优操作打下坚实的基础。

2.2 探索和开发转换方式改进

在原哈里斯鹰算法中, 进行探索和开发的转换是由逃逸能量$E$来决定的, 当$|E| \geqslant 1$时, 进行探索操作, $|E|<1$时, 进行开发操作。由公式(1) 可知, 当算法迭代达到最大迭代次数的一半之后, $|E|$的值恒小于1, 因此算法不会进行探索操作, 即当迭代次数大于$T / 2$时, 算法只进行局部搜索。若当前迭代中搜寻到的最优解未在全局最优解所在区域中, 则算法可能会陷人局部最优, 因此在算法迭代的后半部分, 也需要一定的概率进行全局搜索, 防止算法陷人局部最优。针对HHO算法存在的问题, 本文重新设计一种探索和开发的转换方式, 转换公式为

$ E_{T}=\sin (t {\rm{ \mathsf{ π} }} / 2 T+{\rm{ \mathsf{ π} }})+1, $

(8)

即生成一个[0, 1]间的随机值$r$, 若$r \leqslant E_{T}$, 进行探索操作, 否则进行开发操作。在算法刚开始迭代时, 以大概率进行探索操作, 可以有效搜索到最优解存在的区域; 随着迭代的进行, 探索的概率逐渐减小, 但仍保留一定的概率进行全局搜索, 防止算法过早陷人停滞。因此$E_{T}$初始值为1, 随着迭代的进行逐步减小, 当达到迭代最大次数时其值为0。

2.3 探索方式改进

在HHO算法的探索阶段利用公式(3)进行位置更新，采用两种方式进行探索操作。由于采用原更新方式过于依赖当前种群，不能确保完整地搜索到最优解空间区域。本文将麻雀搜索算法中发现者位置更新公式引入HHO探索阶段，麻雀搜索算法中发现者位置更新公式为

$ \boldsymbol{X}_{i}(t+1)= \begin{cases}\boldsymbol{X}_{i}(t) \cdot \exp (-i / \alpha T), & R <S T, \\ \boldsymbol{X}_{i}(t)+Q \cdot \boldsymbol{L}, & R \geqslant S T, \end{cases} $

(9)

其中: $\alpha$为$[0, 1]$间的随机数; $Q$为一个服从正态分布的随机数; $\boldsymbol{L}$为一个元素全为1的$1 \times D$维矩阵; $R$为预警值, 是一个$[0, 1]$间的随机数; $S T$为$[0.5$, 1] 间的安全阈值。当$R <S T$时, 此时进行广泛搜索。麻雀搜索算法中位置更新公式能够依靠当前个体进行广泛随机搜索, 并且随着迭代次数的增多, 搜索步长随之变化, 有效提高了算法的全局搜索能力。在算法迭代初期, 应进行大范围搜索, 当迭代到后期时, 需要进行小范围更精细的搜索, 因此引人权重因子对发现者公式进一步改进, 权重因子计算公式为

$ w=1-\sin (({\rm{ \mathsf{ π} }} t) /(2 T)) \text { 。} $

(10)

改进后的HHO探索阶段公式为

$ \begin{aligned} & \boldsymbol{X}_i(t+1)= \\ & \begin{cases}w \cdot \boldsymbol{X}_i(t) \cdot \exp (-i /(\alpha T)), & q \geqslant 0.5, \\ \left(\boldsymbol{X}_r(t)-\boldsymbol{X}_{m}(t)\right)-r_3\left(l b-r_4(u b-l b)\right), & q <0.5 。\end{cases} \end{aligned} $

(11)

2.4 柯西-高斯变异扰动

在HHO算法迭代后期，多个个体容易聚集，导致陷入局部最优的风险增大。为防止算法陷入停滞，引入柯西-高斯变异策略。在每次迭代结束时，选取适应度最优的个体进行柯西-高斯变异，若变异后的位置优于当前位置，则选择位置较好的个体进入下一次迭代。柯西-高斯扰动公式为

$ \boldsymbol{U}_{\text {best }}^{t}=\boldsymbol{X}_{r}^{t}\left[1+\lambda_{1} Cauchy(0, 1)+\lambda_{2} Gauss(0, 1)\right] \text {, } $

(12)

其中: $\boldsymbol{U}_{\text {best }}^{t}$表示第$t$次迭代中变异后的位置; $Cauchy(0, 1)$和$Gauss(0, 1)$分别是满足柯西分布和高斯分布的随机变量; $\lambda_{1}=1-t^{2} / T^{2}$随着迭代逐渐减小; $\lambda_{2}=t^{2} / T^{2}$随着逐渐增大。

柯西分布具有较强的扰动能力，可以提高算法的全局搜索能力，高斯分布可以增强算法的局部开发能力。在迭代初期，λ₁值较大，此时主要进行柯西扰动，使HHO在大范围内进行扰动，提高算法的全局搜索能力。当进入迭代后期时，λ₁减小而λ₂增大，此时主要进行高斯扰动，使HHO在猎物位置附近进行搜索，增强算法局部开发能力，提高收敛精度。

2.5 算法流程

IHHO算法步骤如下。

1) 设置种群数量N、最大迭代次数T、问题上下界ub和lb、问题维度dim；2) 利用佳点集初始化种群，计算适应度值；3) 更新逃逸能量E和转换参数E_T；4) 根据E_T选择探索或开发操作；5) 对迭代最优解进行柯西-高斯扰动；6) 重复步骤3)~5)，直到达到最大迭代次数或满足条件。

3 仿真实验结果与分析 3.1 仿真实验环境

本文的仿真实验基于Intel(R) Core(TM) i5-6300HQ CPU@2.30 GHz，8 GB内存，以及Windows10操作系统，仿真软件为Matlab R2021a。

3.2 对比算法及参数选择

本文选取较新提出的群智能优化算法进行对比实验，选择的算法有鲸鱼优化算法^[1](WOA)、花卉授粉算法^[2] (FPA)、蝴蝶优化算法^[3](BOA)、正弦优化算法^[4] (SCA)、麻雀搜索算法^[5] (SSA)。为保证实验的公平性，每个算法独立运行30次，种群大小均为30，最大迭代次数为500，参数选择参考原算法文章中选择的参数，其中：WOA中$a=2-2 t / T$; FPA中$P=0.1$; BOA中$c=0.01, b=0.025, P=$ $0.8, a=0.1$; SCA中$a=2, r_{2} \in[0, 2 {\rm{ \mathsf{ π} }}], r_{3} \in[-2$, $2], r_{4} \in[0, 1]$; SSA中$S T=0.8, \alpha, \beta \in[0, 1], K \in$ $[-1, 1]$; 在HHO中$\beta=1.5, r_{1}-r_{5}, l, m$为$[0, 1]$间的随机数, $E_{0}$为$[-1, 1]$间的随机数, $J$为$[0, 2]$间的随机数。

3.3 测试函数

为验证本文提出的IHHO算法在求解优化问题上的有效性，选择6个标准测试函数进行测试。利用单峰测试函数测试算法局部寻优能力，高峰测试函数用来测试算法的全局探索能力。其测试函数结果如表 1所示。其中F1~F4为单峰测试函数，F5、F6为多峰测试函数，具体公式为

$ \begin{array}{l} F_{1}(x)=\sum\limits_{i=1}^{n} x_{i}^{2}, \\ F_{2}(x)=\sum\limits_{i=1}^{n}\left|x_{i}\right|+\prod\limits_{i=1}^{n}\left|x_{i}\right|, \\ F_{3}(x)=\sum\limits_{i=1}^{n}\left(\sum\limits_{j=1}^{i} x_{j}\right)^{2}, \\ F_{4}(x)=\max \left\{\left|x_{i}\right|, 1 \leqslant i \leqslant n\right\}, \\ F_{5}(x)={\rm{ \mathsf{ π} }} / n\left\{10 \sin \left({\rm{ \mathsf{ π} }} y_{i}\right)+\right. \\ \left.\sum\limits_{i=1}^{n-1}\left(y_{i}-1\right)^{2}\left[1+10 \sin ^{2}\left({\rm{ \mathsf{ π} }} y_{i+1}\right)\right]+\left(y_{n}-1\right)^{2}\right\}+ \\ \sum\limits_{i=1}^{n} u\left(x_{i}, 10, 100, 4\right), \\ F_{6}(x)=0.1\left\{\sin ^{2}\left(3 {\rm{ \mathsf{ π} }} x_{1}\right)+\sum\limits_{i=1}^{n}\left(x_{i}-1\right)^{2} .\right. \\ {\left[1+\sin ^{2}\left(3 {\rm{ \mathsf{ π} }} x_{i}+1\right)\right]+\left(x_{n}-1\right)^{2} \cdot} \\ \left.\left[1+\sin ^{2}\left(2 {\rm{ \mathsf{ π} }} x_{n}\right)\right]\right\}+\sum\limits_{i=1}^{n} u\left(x_{i}, 5, 100, 4\right) 。\end{array} $

3.4 实验结果对比与分析

为对比各算法求解测试函数精度，对其最优值(Best)、平均值(Mean)和标准差(Std)进行比较。最优值反映算法最好的求解能力，平均值反映算法求解问题的平均精度，标准差反映算法的稳定性，各项最优结果在表中均加黑表示。其实验结果如表 1所示，表 1展示的是问题维度在30的情况下实验测试的数值。

表 1列出了本文提出的IHHO算法与其他6种算法在6个测试函数上的对比结果。对于单峰测试函数F1~F4，IHHO算法在30次独立运行中均能找到最优值，与原HHO算法相比性能提升较大；在多峰测试函数F5和F6中，SSA性能表现最好，IHHO算法次之，但与原HHO算法相比，IHHO算法在平均值方面提高了约一个数量级，最优值比HHO有了大幅度的提升，且相比HHO，IHHO算法更加稳定。

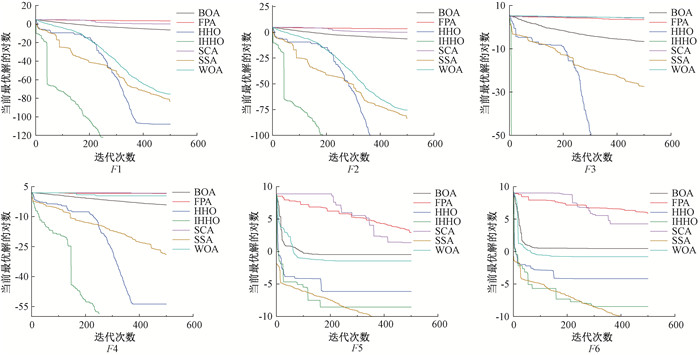
3.5 收敛性对比与分析

为进一步验证本文提出的IHHO算法的性能，将IHHO算法在6个测试函数上的收敛性与表 1中其他智能算法进行对比，如图 2所示。在6个测试函数中，IHHO算法表现优越，其收敛速度与收敛精度远好于其他智能算法。在F1~F4中，IHHO算法收敛最快，在迭代200次左右时收敛到理论最优值，且在F3测试函数中，IHHO算法在刚开始迭代时就已找到最优值。在F5和F6中，IHHO与HHO相比，收敛精度更高，并且多次出现拐点，更容易跳出局部最优。

3.6 不同改进哈里斯鹰算法对比

为进一步验证本文提出的IHHO算法的优越性，将IHHO算法与最新提出的几种改进的哈里斯鹰算法进行对比，利用遗传因子增强的哈里斯鹰算法(HHOCM)^[14]、带探索因子和随机游走策略的哈里斯鹰算法(ERHHO)^[15]、全局优化和自适应相对反射的哈里斯鹰算法(ARHHO)^[16]。算法种群数量都为30，迭代次数都为500，将函数平均值(Mean)和标准差(Std)作为评价指标，其中HHOCM、ERHHO、ARHHO实验数据来自其参考文献，对比结果如表 2所示。

由表 2可知，本文提出的IHHO算法在6个基准测试函数上的性能相比其他改进的哈里斯鹰算法具有极强的竞争力。在F1~F4中，IHHO算法与ERHHO算法表现相同，都能寻得最优值, 寻优精度和稳定性都明显优于HHOCM和ARHHO算法。在F5和F6这两个测试函数中，IHHO算法的性能表现最好，ERHHO算法次之，ARHHO算法排第三，HHOCM算法排第四。总体而言，IHHO算法的搜索精度和稳定性比其他改进的HHO算法具有很强的竞争力。

3.7 改进策略有效性分析

为验证本文提出改进策略的有效性，将采用佳点集改进的HHO-1、探索方式改进后的HHO-2、采用柯西-高斯变异的HHO-3和HHO算法与IHHO算法进行对比。每个测试函数独立运行30次，最终实验结果取其平均值，实验结果如表 3所示。

通过表 3可知，在测试函数F1、F2和F4中，HHO-2都能寻得最优值，对融合算法起到决定性作用。在全部测试函数中，所有改进策略相比原HHO算法，均有不同程度的提高，但多策略融合后的IHHO算法相比于HHO算法提升最大。通过上述数据对比，进一步验证了各个改进策略的有效性及融合多策略后的IHHO算法的优越性。

4 结论

针对HHO算法在探索和开发不平衡、易于陷入局部最优等缺陷，本文提出了一种多策略融合的IHHO算法。IHHO利用佳点集初始化种群，增强种群的多样性；通过自适应参数改进了探索与开发的转换方式，平衡了算法的探索与开发；结合麻雀算法改进了HHO中探索操作，进一步提高了算法的全局搜索能力；利用柯西-高斯变异，防止算法陷入局部最优。将IHHO算法与较新提出的智能优化算法和其他改进的HHO算法在6个基准测试函数中进行实验对比，并分析不同改进策略的有效性。后续工作考虑用IHHO算法解决实际工业优化问题，推广其应用领域。