城镇化进程的持续推进使城市停车规模不断扩大,尤其是在商业、医疗、教育等人口集中地区,停车难已逐渐成为一种社会问题。机械式立体停车库是一种建筑与机械相结合的新兴产物,它可将平面停车转变为立体停车,是解决停车问题的有效方案。
立体停车结构即立体车库支撑框架, 由于其荷载工况的特殊性[1-2],除静力荷载、地震、风荷载外,立体停车结构在服役期间还常承受因提升、横移车辆造成的交变荷载。在交变载荷的作用下,即使最大应力远低于材料的静态强度,经过一定时间也可能发生疲劳破坏[3]。目前,国内外对钢结构疲劳的研究主要集中在钢制桥梁、工业厂房等方面。李贞新等[4]对钢桁拱桥拱桁交叉节点连接结构进行了疲劳试验研究。张清华等[5]提出了一种针对钢桥面板纵肋对接焊缝疲劳开裂的主动加固方法。赵晓青等[6]对我国现行规范中工业厂房钢吊车梁疲劳荷载的取值方法进行了修正。郭华泾等[7]研究了工业厂房钢吊车梁的疲劳损伤演化和复合型疲劳裂纹扩展过程。然而,对于立体停车结构这种新型结构体系,其疲劳方面的研究还极不成熟。一方面,针对特殊荷载工况下的立体停车结构体系。目前无相应的疲劳寿命计算方法;另一方面,进行疲劳分析前需确定合适的荷载谱,但常见的疲劳荷载谱大多针对桥梁及工业厂房建立,车库结构并不适用。因此,有必要针对立体停车结构进行专门的抗疲劳性能研究,制定适用于该类结构的疲劳荷载谱以及疲劳寿命计算公式,用以指导相关工程的抗疲劳设计。
本文基于概率统计方法建立了立体停车结构车辆横移荷载谱,对梁柱节点进行了抗疲劳性能研究,并提出了疲劳寿命经验计算公式。所提荷载谱与计算公式,是立体车库抗疲劳设计方面的重要补充,对相关产业的发展具有促进作用。
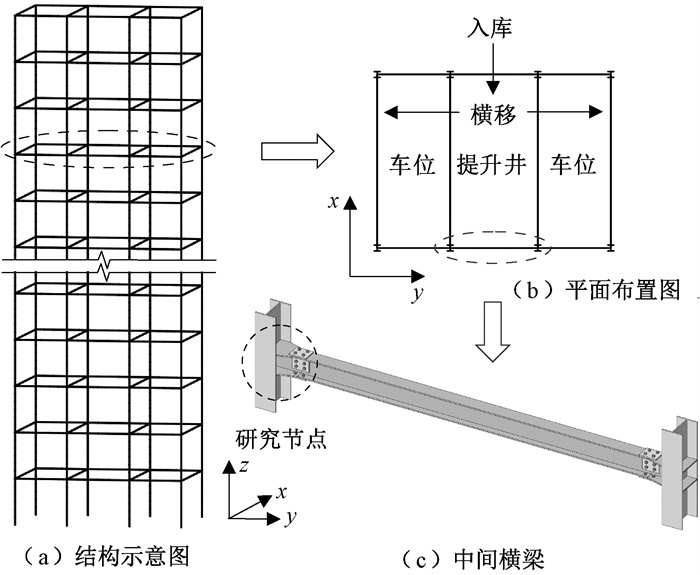
1 钢制立体停车结构体系 1.1 立体停车结构受荷特征垂直升降式立体停车结构层数常为20层(车位数为38个),其布置形式与中间横梁位置示意图如图 1(a)~(c)所示。在车辆横移期间,中间横梁受荷次数多,梁端弯矩大,梁柱节点为疲劳分析的关键部位。因此,本文将针对立体停车结构中间横梁的梁柱节点展开疲劳研究。
|
图 1 立体停车结构示意图 Fig. 1 Diagram of tridimensional parking structure |
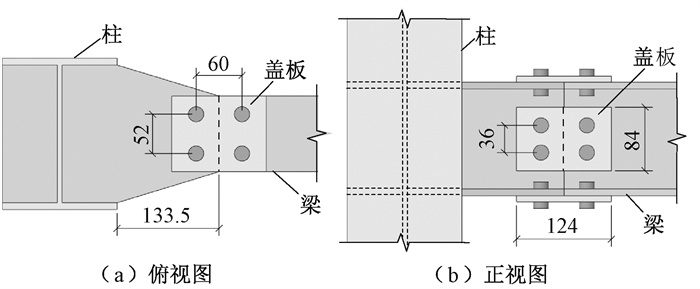
钢制立体停车结构通常采用装配化施工方法,其节点一般为全栓连接形式。为研究梁、柱尺寸对节点疲劳寿命的影响,本文将针对表 1所示的4个全栓连接梁柱节点进行疲劳分析,节点详图如图 2所示,图中数据单位均为mm,盖板厚度均取8 mm。
|
|
表 1 节点梁、柱尺寸 Tab. 1 Dimensions of beam and column of joints |
|
图 2 梁柱节点详图 Fig. 2 Details of beam-column joints |
荷载谱的建立是对立体停车结构进行疲劳分析的前提。本节首先通过对某园区实测停车数据[8]的分析,获得了一个周期内荷载作用的频次特征;然后根据汽车的车型销量及质量确定了荷载幅值的分布规律;最后依据横移荷载的频次特征和分布规律建立了车辆横移荷载谱。
2.1 横移荷载加载次数计算横移荷载频次即车位停车次数可以根据车位占用时长及车辆平均停放时长计算。将一天划分为24个时段,为方便荷载谱的表示,以30天为荷载谱周期,一个周期内单个车位占用时长为ta,计算公式为
| $ t_{\mathrm{a}}=\sum\limits_{i=1}^{24} \frac{D t_{\mathrm{h} i}}{N}, $ | (1) |
式中:D为一个周期的天数,取30 d;thi为一天中第i个时段所有车位被占用时长总和;N为立体车库车位数,取38个。
某时段内立体停车结构中所有车位占用时长总和th的计算公式为
| $ t_{\mathrm{h}}=\left\{\begin{array}{ll} n_{\mathrm{h}}, & n_{\mathrm{h}}<N_0 \\ N, & n_{\mathrm{h}} \geqslant N_0 \end{array}, \right. $ | (2) |
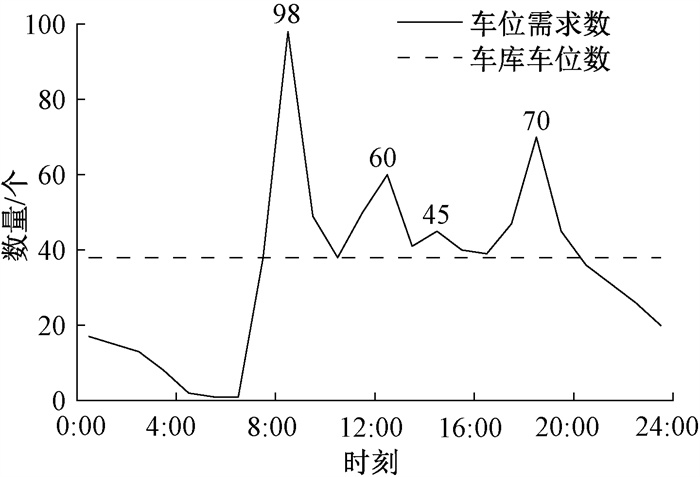
式中:nh为该时段的车位需求数,根据图 3数据取值。
|
图 3 工作日车位需求情况 Fig. 3 Parking requirements for working days |
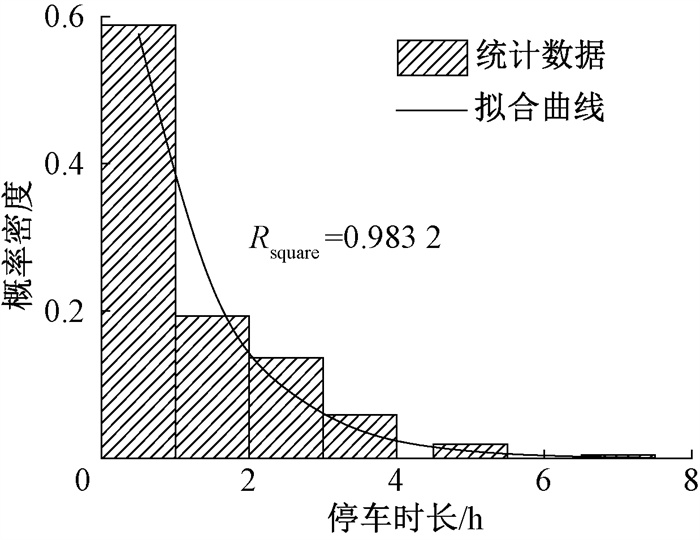
车辆平均停放时长可根据停车时长概率密度函数计算。根据该数据分布特征,使用负指数分布进行拟合,通过决定系数Rsquare(取值范围为0~1)检验拟合优度,该值越接近1,说明拟合效果越好。对后续其他数据的拟合效果均采用该系数进行评价。图 4给出了停车时长的概率分布拟合曲线,拟合所得概率密度函数为
|
图 4 停车时长拟合模型 Fig. 4 Fitting model of parking time |
| $ f(x)= \begin{cases}0.905\;9 \mathrm{e}^{-0.905\;9 x}, & x \geqslant 0 , \\ 0, & x<0, \end{cases} $ | (3) |
因车辆停放时长均在8 h以内,一个周期内单个车位停车次数nz计算公式为
| $ n_{\mathrm{z}}=\frac{F t_{\mathrm{a}}}{T}=\frac{0.966}{1.133} t_{\mathrm{a}}, $ | (4) |
式中:F为停放时长不超过8 h的车辆所占概率密度;T为车辆平均停放时长,即式(1)的期望值。
2.2 横移荷载幅值计算载车板荷载取2.5 kN[9],在前后横梁平均分配。根据《机械式停车设备通用安全要求》[10]规定,车辆荷载在前后横梁按6∶4分配,则横移荷载=0.5×载车板荷载+0.6×车辆荷载,其中车辆荷载包括车载行李质量与汽车质量,行李质量一般按50 kg考虑,汽车质量与车型有关,具有明显随机性。
为确定汽车质量的取值,本文统计并分析了2015—2019年汽车销售市场排名前30的车型销量及质量数据。如图 5所示,考虑数据呈三峰分布,采用混合正态分布模型进行拟合,概率密度函数为
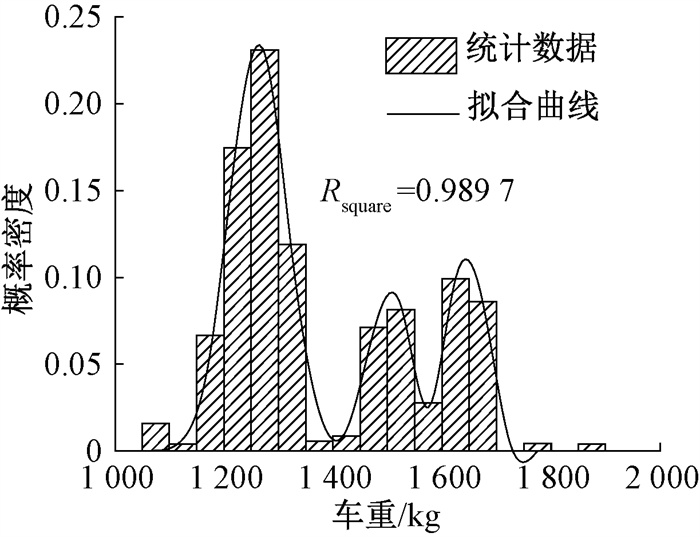
|
图 5 汽车质量拟合模型 Fig. 5 Fitting model of automobile quality |
| $ \begin{aligned} & f(x)=0.235\;6 \mathrm{e}^{-\left(\frac{x-126\;2}{73.25}\right)^2}+ \\ & 0.094\;89 \mathrm{e}^{-\left(\frac{x-150\;5}{54.2}\right)^2}+0.131\;4 \mathrm{e}^{-\left(\frac{x-164\;7}{42.05}\right)^2}, \end{aligned} $ | (5) |
根据式(5)的概率分布规则,利用蒙特卡洛随机抽样方法,可以得到横移荷载幅值。根据横移荷载加载频次特征与幅值分布规律建立的车辆横移荷载谱如图 6所示。
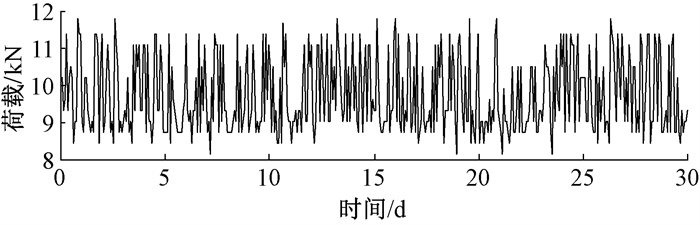
|
图 6 车辆横移荷载谱 Fig. 6 Vehicle transverse load spectrum |
本文通过疲劳分析软件ANSYS nCode DesignLife进行疲劳性能分析,其流程如图 7所示。
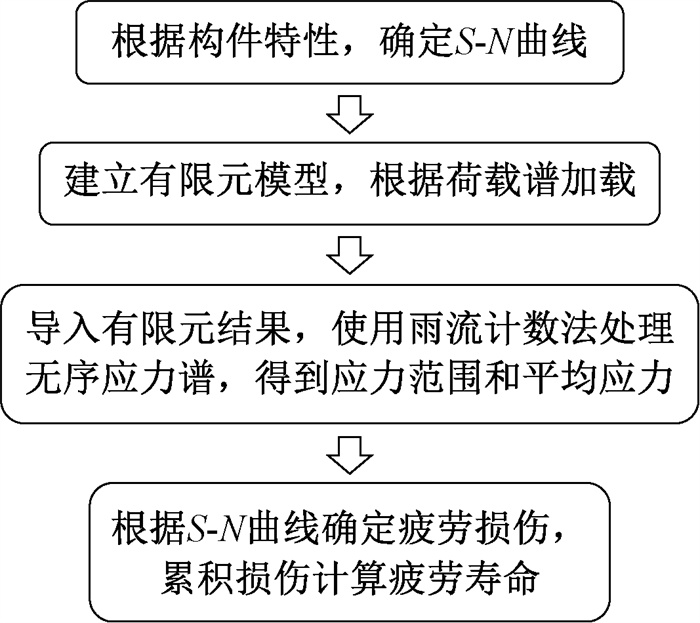
|
图 7 疲劳分析流程图 Fig. 7 Fatigue analysis flow chart |
图 7中S-N曲线为应力幅S与应力循环次数N的关系曲线,通常使用对数坐标表示。对本文所采用的普通钢材(梁、柱、盖板、螺栓)、螺栓孔、焊缝按疲劳计算类别[11]进行分类,分别为Z1、Z2、Z8,其S-N曲线如图 8所示,其中应力幅S的单位为Pa,应力循环次数N的单位为次。
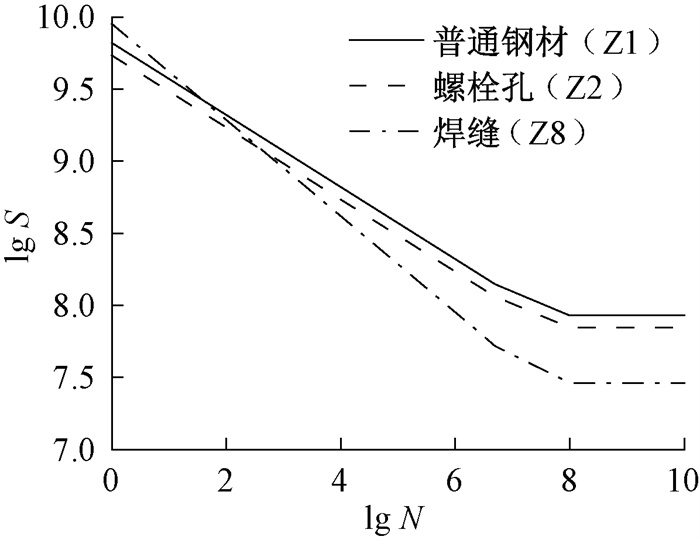
|
图 8 不同部位的材料S-N曲线 Fig. 8 S-N curves of different parts of material |
为验证本文所采用疲劳分析方法的准确性,取文献[12]中试件SJ1-1、SJ1-2、SJ1-3、SJ1-7、SJ1-9作为验证算例与有限元结果进行对比。试件详图如图 9所示,钢板通过角焊缝围焊连接,焊脚尺寸为6 mm,图中数据单位均为mm,试件一端使用螺栓固定,另一端通过机械型振动疲劳试验机加载,以测点1、2测得应力平均值作为名义应力,试件破坏前荷载循环次数即疲劳寿命。采用有限元软件ANSYS Workbench建立的试件有限元模型如图 9(c)所示。
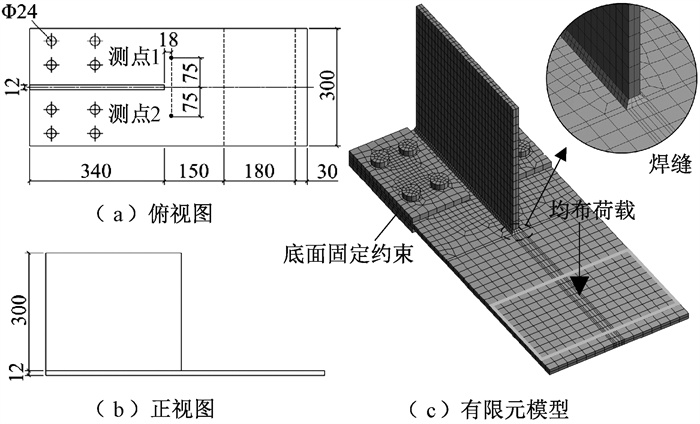
|
图 9 试件详图与有限元模型 Fig. 9 Detail drawing and finite element model of the specimen |
在模型螺栓连接处的下方盖板底面设置固定约束。采用实体单元Solid186模拟钢板、螺栓、盖板和焊缝。摩擦接触单元为Conta174和Targe170,考虑材料接触非线性,各部件之间的相互作用设置如下:钢板间的焊接使用Bonded黏合接触模拟;螺杆和螺栓孔之间为Frictionless无摩擦接触;其他部位均为Frictional摩擦接触,摩擦系数取0.4[13]。
各材料本构关系均使用双线性等向强化模型,弹性模量取206 GPa,材料泊松比取0.3。根据验证算例材料检测结果,钢板屈服强度取453 MPa,抗拉强度取594 MPa,焊缝材料强度与母材一致。采用10.9级M24高强螺栓,屈服强度为940 MPa[14],加载前对螺栓施加225 kN的预紧力[15]。
为满足计算精度及计算成本的要求,进行网格敏感性分析,结果如图 10所示。当焊缝网格尺寸为5.5 mm和3.5 mm时,计算结果已十分接近,综合考虑结果准确度和计算效率,将焊缝网格尺寸设定为5.5 mm。
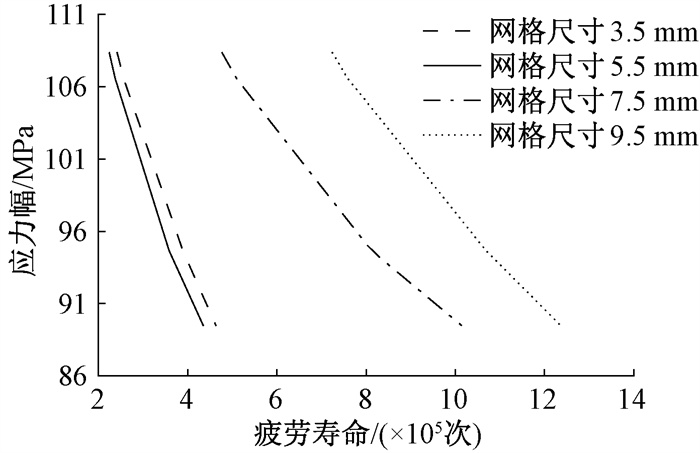
|
图 10 不同焊缝网格尺寸下模型的应力幅-疲劳寿命曲线 Fig. 10 The stress amplitude-fatigue life curves of the model with different weld grid sizes |
对于疲劳破坏位置,由图 11可知验证算例与有限元模拟的疲劳破坏位置均为焊缝包角处。对于疲劳寿命,由表 2可知,有限元结果总体上与验证算例吻合较好,当应力幅为106.71、89.30 MPa时,有限元结果与验证算例结果的偏差较大,分别为24.72%、18.15%。观察发现,在上述应力幅下验证算例结果存在明显波动,这与传统S-N曲线的特征是矛盾的,导致该现象的原因可能是试件在焊缝的初始缺陷、焊接条件等方面存在差异。综上可知,本文采用的疲劳分析方法有较高准确度。
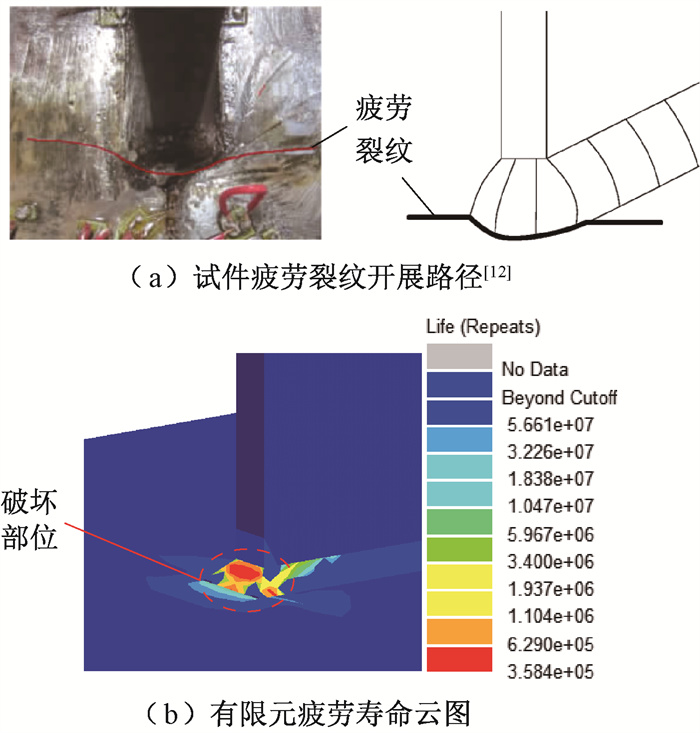
|
图 11 验证算例与有限元分析破坏位置对比 Fig. 11 Comparison of fatigue failure location between test and finite element analysis |
|
|
表 2 本文验证算例与有限元分析疲劳寿命对比 Tab. 2 Comparison of fatigue life between test and >finite element analysis |
采用验证的数值方法建立表 1中4个节点的有限元模型,以节点PL-1为例,图 12给出了其有限元模型局部示意图。根据停车功能需求与文献[16],横梁跨度取3 m,节点柱高取0.7 m,轴压比按中间楼层考虑取0.15。
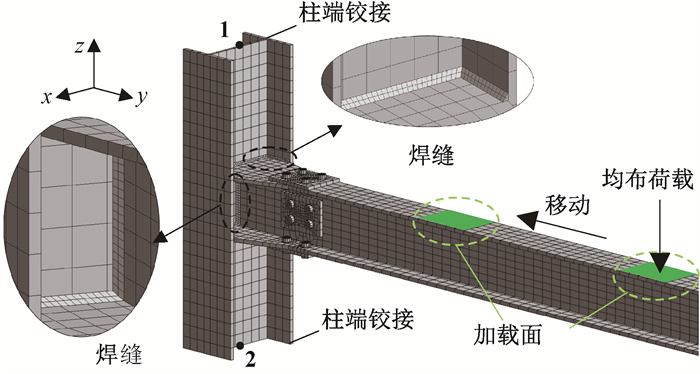
|
图 12 节点PL-1有限元模型 Fig. 12 Finite element model of joint PL-1 |
将柱顶面与点1(柱顶面形心)进行自由度耦合,约束点1的x、y方向平动和y、z方向转动;将柱底面与点2(柱底面形心)进行自由度耦合,约束点2三个方向的平动和y、z方向的转动,以模拟柱两端的铰接。采用实体单元Solid186模拟梁、柱、盖板、螺栓和焊缝,并在焊缝处加密模型网格。根据网格敏感性分析结果,焊缝网格尺寸取5.5 mm。摩擦接触单元为Conta174和Targe170,考虑材料接触非线性,模型各部件之间的相互作用设置如下:梁、柱间的焊缝连接使用Bonded粘合接触模拟;螺杆和螺栓孔之间为Frictionless无摩擦接触;其他部位均为Frictional摩擦接触,摩擦系数取0.4[13]。
各材料本构关系均采用双线性等向强化模型,材料弹性模量取206 GPa,泊松比取0.3。参考文献[17],梁、柱、盖板的材料屈服强度取330 MPa,焊缝材料强度与母材一致。采用10.9级M12高强螺栓,屈服强度为940 MPa[14],加载前对螺栓施加55 kN的预紧力[15]。
车辆存、取过程对结构的作用效果相同。如图 12所示,依次将竖向均布荷载作用于相邻的9个加载面,以模拟载车板的移动,均布荷载幅值根据荷载谱分布规律而变化,以模拟横移具有不同质量的汽车。根据常见设备参数,车辆横移速度取0.3 m/s。
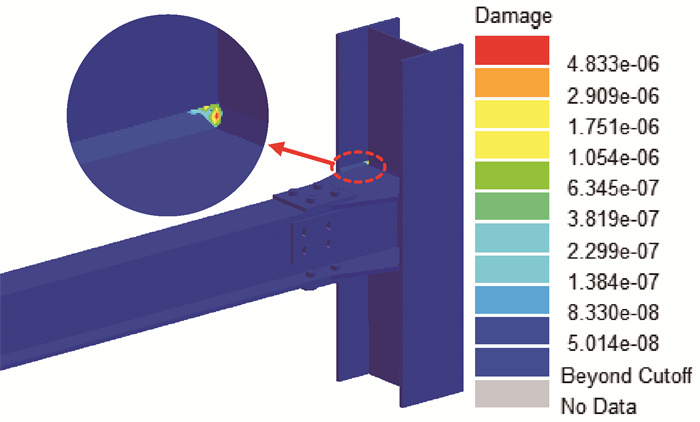
节点PL-1疲劳寿命计算结果为64.63 y,由图 13可知,疲劳破坏首先发生在梁柱翼缘交接部位的焊缝处,且该位置疲劳寿命远小于其他部位,最大差距为96.39倍,在实际工程的抗疲劳设计中,应重点关注该部位的应力变化情况。
|
图 13 节点PL-1疲劳损伤云图 Fig. 13 Fatigue damage of joint PL-1 |
为深入揭示立体停车结构梁柱节点在横移荷载作用下的疲劳损伤机理,本节探讨节点截面尺寸、轴压比和轨道偏心距对节点疲劳寿命的影响。
5.1 构件尺寸影响表 1中节点PL-1、PL-2、PL-3、PL-4的疲劳寿命计算结果分别为64.63、54.40、68.53、48.91 y,由此结果可知当梁截面面积基本不变,梁截面高度增加20%时,节点PL-1疲劳寿命较PL-2增加了18.81%,节点PL-3较PL-4增加了40.11%;当柱截面面积基本不变,柱截面高度提高33.33%时,节点PL-1疲劳寿命较PL-3减少5.69%,节点PL-2较PL-4增加了11.22%。可以发现,相较于柱截面高度,梁截面高度的增大对节点疲劳寿命的延长作用更为显著。因此,在需要控制用钢量的前提下,可以通过保持梁截面面积不变并增大梁截面高度增加节点疲劳寿命。
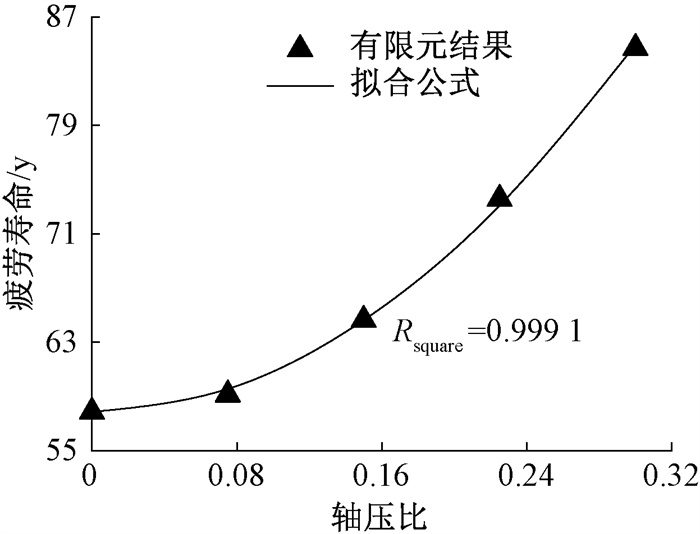
5.2 轴压比影响为讨论柱轴压比对节点疲劳寿命的影响,计算并比较节点PL-1在不同柱端轴压比下的疲劳寿命。考虑立体停车结构轴压比变化范围,设置轴压比为0、0.075、0.150、0.225、0.300。由图 14可知,当轴压比在0~0.3之间时,其值越大,节点疲劳寿命越长。这是因为轴压比增大时,焊缝初始应力也增大,导致应力幅减小,疲劳寿命随之增加。如图 14所示,对计算结果进行拟合,得到
|
图 14 不同轴压比下节点疲劳寿命及拟合曲线 Fig. 14 Fatigue life of joints with different axial compression ratios and fitting curve |
| $ N_{\mathrm{u}}=a_{\mathrm{u}} u^2+N_{\mathrm{u} 0}, $ | (6) |
式中:Nu为节点疲劳寿命;au为与节点材料、尺寸相关的参数,对于节点PL-1取301;u为柱端轴压比;Nu0为轴压比为0时的节点疲劳寿命。
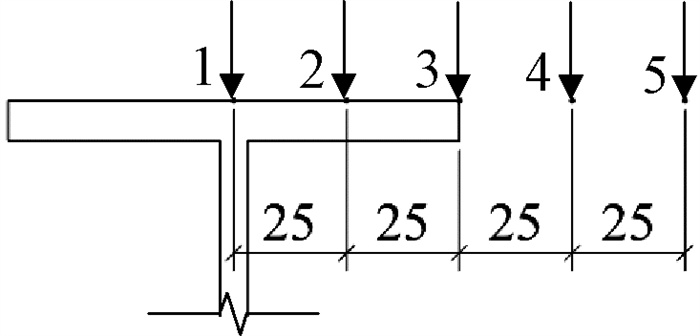
5.3 轨道偏心距影响实际工程中横移轨道不一定位于横梁翼缘中线上。为探讨轨道偏心距的影响,如图 15所示(图中数据单位为mm),通过有限元软件ANSYS Workbench的Remote Force远端力功能,分别在节点PL-1的横梁上点1~5处加载并计算节点疲劳寿命,其中点1为轨道不偏心时的加载点。
|
图 15 偏心加载示意图 Fig. 15 Diagram of eccentric loading |
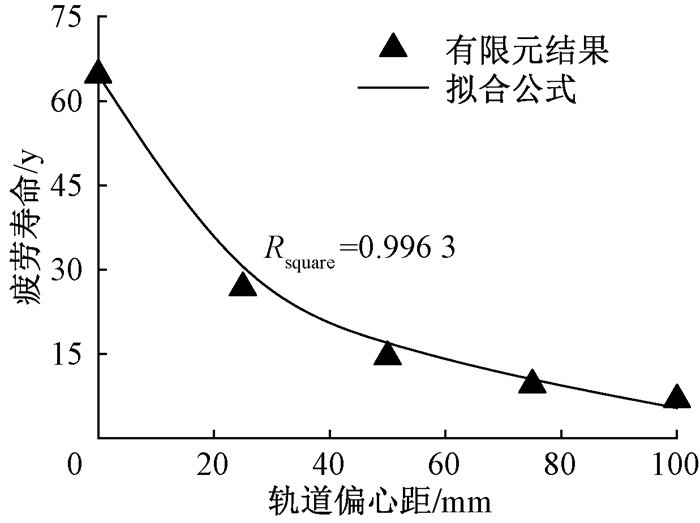
对疲劳寿命计算结果进行拟合,拟合曲线如图 16所示,所得经验计算公式为
|
图 16 不同轨道偏心距下节点疲劳寿命及拟合曲线 Fig. 16 Fatigue life of joints with different track eccentricity and fitting curve |
| $ N_1=a_1 l^{0.3}+\mathrm{N}_{10} \text {, } $ | (7) |
式中:Nl为节点疲劳寿命;al为与节点材料、尺寸相关的参数,对于节点PL-1取-14.89;l为轨道偏心距;Nl0为轨道不偏心时的节点疲劳寿命。
由图 16可知,随着轨道偏心距的增加,节点疲劳寿命明显缩短,这是轨道偏心产生的附加弯矩引起焊缝应力幅增大所导致的。当轨道由横梁翼缘中线移至边缘,节点疲劳寿命大幅缩短,降幅为78%,因此,建议在工程设计中对横移轨道偏心距进行严格控制。
6 计算公式验证本文所提疲劳寿命计算公式(6)、(7)的适用性可通过经典的断裂力学法[18]进行验证,该方法计算疲劳寿命公式为
| $ N_{\mathrm{p}}=\frac{1}{C \Delta \sigma^m k^m(1-m n)}\left[a_{\mathrm{c}}^{1-m n}-a_0^{1-m n}\right], $ | (8) |
式中:Np为疲劳裂纹扩展寿命;Δσ为焊件应力变化范围;C、m为疲劳裂纹扩展参数,C取4.6×10-13,m取3;k、n为取决于焊件几何形状的参数,k取2.2,n取0.66;ac为临界裂纹尺寸,可假定ac=B/2+l[18],B为板厚,l为焊脚长,得ac为9 mm;a0为初始缺陷尺寸, 取0.21 mm。
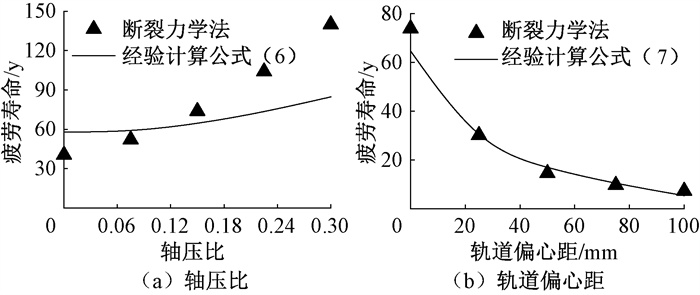
经验计算公式结果与断裂力学法结果的对比情况如图 17所示。在立体停车结构常见的轴压比范围0.075~0.225内,式(6)有较好的精度,平均误差为18.36%;当轴压比为0或0.3时,式(6)与断裂力学法的结果存在较大偏差,分别为42.83%、39.47%。但在实际工程中,轴压比接近0的情况并不多见,且当轴压比较大时,经验公式所得为偏安全的结果。因此,可以认为在通常情况下经验计算公式是合理的。由图 17(b)可知,在0~100 mm范围内的不同轨道偏心距下,式(7)结果与断裂力学法结果吻合较好,平均误差为6.48%。综上可知,本文所提经验计算公式有较强的适用性,可为估算轴压比与轨道偏心距对立体停车结构疲劳寿命的影响提供参考。
|
图 17 经验公式与断裂力学法计算结果对比 Fig. 17 Comparison of calculation results between the computing formula and fracture mechanics method |
本文建立了适用于立体停车结构的车辆横移荷载谱,实现了考虑实际车辆停放规律的抗疲劳分析,解决了该类结构的疲劳研究中缺少荷载谱的问题。在车辆横移荷载作用下,梁柱翼缘交接处的焊缝为节点中最先发生疲劳破坏的敏感部位,工程设计中应重点关注该部位的应力变化情况。在梁截面面积不变时增加梁截面高度可有效提高节点疲劳寿命;柱轴压比越大,节点疲劳寿命越长;轨道偏心距增大会导致节点疲劳寿命大幅缩短,建议对立体停车结构的横移轨道偏心距进行严格控制。本文所提疲劳寿命经验计算公式可作为立体停车结构抗疲劳设计的参考依据。
| [1] |
XIANG S Y, HE Y J, ZHOU X H. Behaviour and failure modes of steel parking structure column under transverse impact[J]. Thin-walled structures, 2021, 167: 108163. DOI:10.1016/j.tws.2021.108163 (  0) 0) |
| [2] |
HE Y J, ZHOU X H, LIU X H. Dynamic response of the high-rise steel tridimensional parking structure for vertical impact excitation of the lifting system[J]. The structural design of tall and special buildings, 2015, 24(12): 779-796. DOI:10.1002/tal.1211 (  0) 0) |
| [3] |
岑昆, 王明星. 电解低钛铝制备铝硅合金的疲劳裂纹扩展行为[J]. 郑州大学学报(理学版), 2009, 41(3): 43-49. CEN K, WANG M X. Fatigue crack growth behavior in the Al-Si alloys prepared using electrolytic low-titanium aluminum[J]. Journal of Zhengzhou university (natural science edition), 2009, 41(3): 43-49. (  0) 0) |
| [4] |
李贞新, 强士中, 卫星, 等. 大跨度钢桁拱桥拱桁交叉节点疲劳试验研究[J]. 铁道学报, 2010, 32(4): 79-83. LI Z X, QIANG S Z, WEI X, et al. Fatigue tests of arch truss cross joints of long-span rail-cum-road bridge[J]. Journal of the China railway society, 2010, 32(4): 79-83. DOI:10.3969/j.issn.1001-8360.2010.04.015 (  0) 0) |
| [5] |
张清华, 朱金柱, 陈璐, 等. 钢桥面板纵肋对接焊缝疲劳开裂主动加固方法研究[J]. 桥梁建设, 2021, 51(2): 18-25. ZHANG Q H, ZHU J Z, CHEN L, et al. Research on a positive reinforcement method for fatigue cracking in longitudinal rib butt welds of orthotropic steel bridge deck[J]. Bridge construction, 2021, 51(2): 18-25. (  0) 0) |
| [6] |
赵晓青, 岳清瑞, 郭小华, 等. 钢吊车梁疲劳评估欠载效应的等效系数法研究[J]. 建筑结构学报, 2021, 42(1): 179-188. ZHAO X Q, YUE Q R, GUO X H, et al. Study on underload effect equivalent coefficient method for fatigue evaluation of steel crane beams[J]. Journal of building structures, 2021, 42(1): 179-188. (  0) 0) |
| [7] |
郭华泾, 崔鹏飞, 吴佰建, 等. 既有工业厂房钢吊车梁疲劳性能预后分析[J]. 哈尔滨工业大学学报, 2019, 51(6): 109-115. GUO H J, CUI P F, WU B J, et al. Fatigue prognosis analysis on existing steel industrial crane runway girders[J]. Journal of Harbin institute of technology, 2019, 51(6): 109-115. (  0) 0) |
| [8] |
吕双. 基于排队论的立体车库泊位规模和车辆存取速度计算方法研究[D]. 北京: 北京交通大学, 2017. LYU S. Research on the stereo garage scale and access speed based on queuing theory[D]. Beijing: Beijing Jiaotong University, 2017. (  0) 0) |
| [9] |
贺拥军, 周绪红, 何佳琦. 隔层桁架式立体停车结构地震倒塌易损性分析[J]. 湖南大学学报(自然科学版), 2014, 41(4): 10-15. HE Y J, ZHOU X H, HE J Q. Seismic collapse fragility analysis of the 3D parking structure with alternation story-height truss lateral-load-resisting system[J]. Journal of Hunan university (natural sciences), 2014, 41(4): 10-15. (  0) 0) |
| [10] |
中华人民共和国国家市场监督管理总局, 中国国家标准化管理委员会. GB 17907—2010E, 机械式停车设备通用安全要求[S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. GB 17907—2010E, Mechanical parking systems-General safety requirement[S]. Beijing: Standards Press of China, 2011. (  0) 0) |
| [11] |
中华人民共和国住房和城乡建设部. GB 50017—2017, 钢结构设计标准[S]. 北京: 中国建筑工业出版社, 2017. Ministry of housing and Urban-Rural Development of the People's Republic of China. GB 50017—2017, Standard for design of steel structures[S]. Beijing: China Architecture & Building Press, 2017. (  0) 0) |
| [12] |
田圆, 吉伯海, 杨沐野, 等. 钢桥面板顶板与竖向加劲肋连接角焊缝疲劳试验[J]. 河海大学学报(自然科学版), 2014, 42(5): 433-438. TIAN Y, JI B H, YANG M Y, et al. Fatigue experimental investigation of steel bridge deck plate and vertical stiffener connection fillet weld[J]. Journal of hohai university (natural sciences), 2014, 42(5): 433-438. (  0) 0) |
| [13] |
赵文占, 郭剑云. 新型隔板贯通式钢梁-矩形管钢柱节点力学性能研究[J]. 工业建筑, 2021, 51(8): 87-92. ZHAO W Z, GUO J Y. Study on mechanical properties of joints connecting h-shaped steel beam and rectangular steel tube column with a new-type diaphragm[J]. Industrial construction, 2021, 51(8): 87-92. (  0) 0) |
| [14] |
中华人民共和国国家市场监督管理总局, 中国国家标准化管理委员会. GB/T 3098.1—2010, 紧固件机械性能——螺栓、螺钉和螺柱[S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. GB/T 3098.1—2010, Mechanical properties of fasteners—Bolts, screws and studs[S]. Beijing: Standards Press of China, 2011. (  0) 0) |
| [15] |
中华人民共和国住房和城乡建设部. JGJ 82—2011, 钢结构高强度螺栓连接技术规程[S]. 北京: 中国建筑工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. JGJ 82—2011, Technical specification for high strength bolt connections of steel structures[S]. Beijing: China Architecture & Building Press, 2011. (  0) 0) |
| [16] |
XIANG S Y, HE Y J, ZHOU X H, et al. Continuous twice-impact analysis of steel parking structure columns[J]. Journal of constructional steel research, 2021, 187: 106989. (  0) 0) |
| [17] |
贺拥军, 刘健飞, 马义飞. 采用新型摩擦耗能节点立体停车结构抗震性能分析[J]. 公路交通科技, 2019, 36(5): 49-56. HE Y J, LIU J F, MA Y F. Analysis on seismic performance of 3D parking structure using new energy dissipation joint[J]. Journal of highway and transportation research and development, 2019, 36(5): 49-56. (  0) 0) |
| [18] |
赵少汴. 抗疲劳设计手册[M]. 北京: 机械工业出版社, 2015: 492-495. ZHAO S B. Manual of anti-fatigue design[M]. Beijing: China Machine Press, 2015: 492-495. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


